基于FPGA的柱面投影算法的实现
2015-10-17武晓斌
武晓斌
(西安电子科技大学 电子工程学院,陕西 西安 710071)
基于FPGA的柱面投影算法的实现
武晓斌
(西安电子科技大学 电子工程学院,陕西 西安 710071)
介绍了圆柱面投影算法的基本原理,给出了基于硬件逻辑实现的系统设计,该设计基于Altera公司Cyclone III系列的FPGA,先将外部数据写入DDR2 SDRAM,然后用硬件逻辑来实现圆柱面投影算法,同时自动生成Cameralink时序提供给后端,并通过显示模块转化输出到LCD的DVI接口进行实时显示,通过显示的图像可看到,硬件逻辑实现的柱面投影达到了预期效果。
FPGA;柱面投影;Cameralink;DDR2 SDRAM
柱面投影技术主要应用于图像拼接领域。把不同视角的图像拼接起来,若不进行投影变换,则在拼接缝处会出现“折线”的现象,所以必须对输入图像进行投影变换[1]。目前一般常用的图像投影变换模型分为球面投影模型、圆柱面投影模型和立方体投影模型[2]。球面投影模型和立方体投影模型对相机镜头的视场角要求较大,这样就造成成本较高,而且运算复杂度较大。系统从原始图像数据采集到图像模型变换,再到投影完成后的显示均使用FPGA进行操作。由于FPGA不适合于大运算量的计算。因此,在FPGA上选择圆柱面投影算法实现较为合适,而且柱面投影算法对相机镜头视场角的要求较小。
1 系统整体设计
系统的数据源是Cameralink时序的图像数据,由于外部进来的图像数据已在工业相机内部进行了图像增强、去噪等处理,所以数据源可以保证较高的质量,无需再进行图像的预处理,这样在外部Cameralink数据进来后便可直接进行柱面投影变换。图1是系统的整体结构设计。
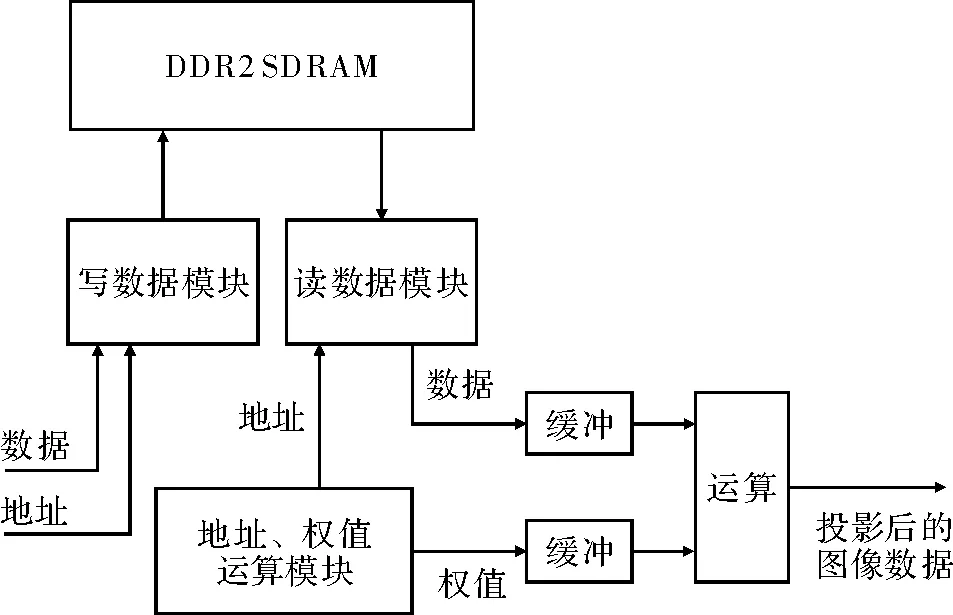
图1 系统整体设计图
2 投影变换
柱面投影模型的理论基础是将相机以一点为中心点,以焦距为半径,旋转360°,拍到的照片形成一个圆柱面。该圆柱面投影算法简单,易于工程实现,且占用的硬件逻辑资源较少。
2.1 投影坐标系
使用相机进行图像采集的过程,是将现实世界的场景投影到相机的二维像平面上,投影的过程就是成像变换的过程。成像变换实现不同坐标系之间的变换,该过程一般包括的坐标系为:
(1)三维世界坐标系,也称为真实的世界坐标系XYZ,表示场景点在客观世界中的绝对坐标。坐标(x,y,z)可准确地定义一个物体在现实世界中的位置。
(2)像平面坐标系,是指相机内部CCD靶面的二维坐标系统,表示场景点在像平面上的投影。一般取像平面与相机坐标系统的xy平面平行,原点位于相机的光轴上。该坐标系与照片所在的坐标系类似。
(3)图像坐标系,是指图像阵列中图像像素的位置,图像处理通常在图像坐标系中进行。在图像坐标系中原点位于图像的左上角,x方向朝右,y方向朝下,像素坐标是整数值。
2.2 像素焦距的估计
在实际中,相机镜头上的焦距是以mm为单位标识,但在图像中计算时,焦距是以像素为单位的。为避免转换带来的麻烦,需要将两种不同的单位统一。因此,需要先将实际场景中每个像素在图像坐标系中的像素坐标表示出来。
对于一般的工业相机可分为机芯和镜头两部分。机芯决定了相机的分辨率,而镜头决定了相机的视场角。一般相机镜头的视场角是已知的,若未知,也可通过拍摄图片进行标定的方法来确定。
此处假设已知相机水平视场角为θ。图2表示了图像宽度W,相机焦距f,相机水平视角θ三者之间的关系。
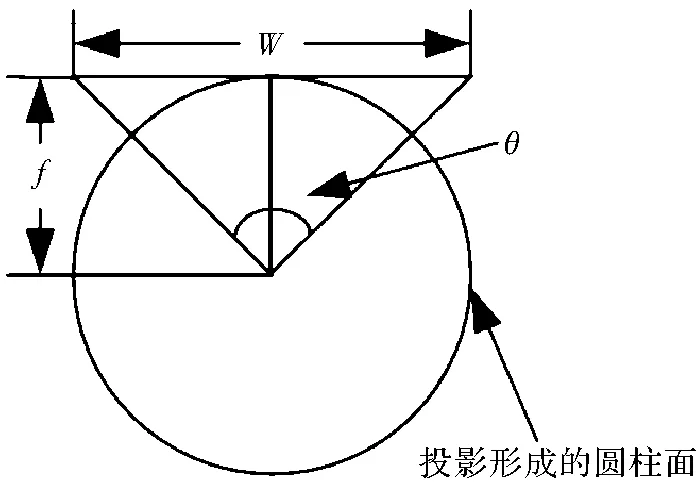
图2 相机焦距与图像宽度关系
估算相机的像素焦距
(1)
其中,W是照相机拍摄到的实景图像宽度。综上,实景图像上任何一个像素点P(x,y)在图3中相机坐标系oxyz下的对应像素坐标为P(xc,yc,zc),两者的对应关系为
(2)
2.3 柱面投影算法
由于采集的原始图像是以相机为圆心,旋转360°所拍摄到的,因此其并不在同一个投影平面上,将拍摄到的各幅图像全部都映射到一个标准的柱面上,即进行柱面投影[3-4]。
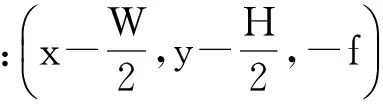

图3 柱面投影变换
照相机坐标系原点与像素点P的直线方程为
(3)
式(3)中,t是参数,圆柱面的方程为
u2+v2=f2
(4)
联立式(3)与式(4)可得
(5)
将式(5)代入式(3)可得
(6)
式(6)中,(u,v,w)是像素点P(x,y)在圆柱面上投影点Q的参数坐标。但Q点的坐标是3个维度的,需将其转换为两个维度的图像坐标才便于运算,即需要将圆柱面展开成平面。变换公式如下
(7)
由式(6)与式(7)可得,实际图像I上任意一个像素点P(x,y)在柱面投影图像上的像素点Q(x′,y′)的投影公式如式(8)所示,由于θ是已知值,故无需将θ进行化简
(8)
由式(8)可推导得出,在实际景物中同一条垂直线上的两个像素点(x,y)和(x′,y′),这两个像素在柱面投影图上的横坐标相同,如式(9)所示
(9)
式(9)说明,对于从实景图像变换到柱面投影图像,图像只会在横坐标方向发生投影变形,而在竖直方向不会发生这种形变。
2.4 柱面投影算法的硬件实现
前面已描述了柱面投影算法的理论原理,但上述推导方法是由实际原始图像坐标去推导柱面投影图像坐标,这对实际的硬件实现中是不方便的。因为,在实际的柱面投影算法实现时,首先得到的是原始图像的像素坐标和像素值,此时需要先将原始图像存到外部存储器DDR2SDRAM中[6],由已知的柱面投影的坐标去推导原始图像对应该坐标的像素的坐标,然后将坐标转化成存储器的地址值,将对应坐标的像素值读出。
因此,需要将上述公式进行逆向推导,变换成由柱面投影像素坐标去计算原始图像的坐标。
(10)
其中,x′,y′分别示柱面投影图像的横坐标与纵坐标;W,H分别为图像的宽和高;θ为相机镜头的水平视场角。
根据柱面投影的像素坐标可计算出该坐标的像素值对应的是原始图像的像素坐标,但通常计算出的原始图像像素坐标为小数,即位于4个像素坐标的中间的空隙处,此时就需要以该坐标周围的4个像素通过插值运算来计算该坐标处的像素值,此处使用双线性插值。
如图4所示,设已知位置函数f在点Q11(x1,y1),Q12(x2,y2),Q21(x2,y1),Q22(x2,y2)位置处的函数值,求点P(x,y)处的函数值。

图4 双线性插值各点位置图
双线性插值分为两个步骤:首先对x方向进行插值,即求出R1(x,y1),R2(x,y2)两点的值,主要思想是根据R1(x,y1)距离Q11(x1,y1),Q21(x2,y1)的距离进行权值分配,离该点距离越近的点,则这一点所占的比例就越大;反之,这一点所占的比例就越小。R2(x,y2)的求解与R1(x,y1)相似。R1(x,y1)与R2(x,y2)两点处的值为
(11)
然后进行y方向上的插值,此时,就是由R1(x,y1),R2(x,y2)两点的值来求解点P(x,y)处的函数值。主要思想是根据P(x,y)距离R1(x,y1),R2(x,y2)的距离进行权值分配,离该点距离越近的点近,则这一点所占的比例就越大;反之,这一点所占的比例就越小。点P(x,y)处的值如下
(12)
由式(11)与式(12)可导出点的值,如下
(13)
由式(13)即可得到双线性插值的结果点P(x,y)处的值。但在进行柱面投影时所使用的坐标系的纵轴方向与上面图示相反,且可确定分母处的值均为1,故在实际使用时双线性插值结果点P(x,y)处的值为
f(P)≈(y-y2)·(x2-x)·f(Q11)+(y-y2)·(x-x1)·f(Q21)+(y1-y)·(x2-x)·f(Q12)+(y1-y)·(x-x1)·f(Q22)
(14)
这就是双线性插值算法,该算法计算量略大,但在FPGA实现时,还可接受,且可得到高质量的图像,不会出现不连续的状况。但由于双线性插值具有低通滤波器的性质,使高频分量受损,所以可能使图像灰度变化较大的部位在一定程度上变得模糊。
3 DDR2 SDRAM外部存储器与操作模块
DDR2SDRAM外部存储器[7]是属于易失性存储器,即掉电后数据就会丢失。系统使用的是镁光公司生产的MT47H32M16外部存储器。由于DDR2SDRAM的读写操作需要较为复杂的操作时序,因此系统使用了Altera公司生产的IP核,对DDR2SDRAM进行控制。该DDR2SDRAM存储器工作在160MHz,其数据端口为16bit,又因其在时钟的上下沿均进行采样,这样使得DDR2SDRAM可达到640Mbit·s-1的高带宽,满足柱面投影所需的带宽需求[8]。
在本系统实现柱面投影和双线性插值模块时,封装在模块内部,输出接口主要有4个地址数据和4个权值数据。因此,就需要DDR2SDRAM控制器的工作频率达到输入图像的工作频率的4倍,至少达到柱面投影模块的工作频率的4倍。DDR2SDRAM控制器的工作频率问题其实是在硬件实现柱面投影时的瓶颈问题。
4 实现结果
由图5可知,下面两路相机同时由FPGA来实现圆柱面投影,其效果较好,可正常显示。但此方法仍存在一些不足,当需要进行柱面投影变换的图像数据量过大时,可能会由于FPGA的工作频率不足而出现问题,这需要在日后提出更好的方案进行解决。

图5 柱面投影效果示意图
5 结束语
本文在原有柱面投影算法均是由DSP等适合高复杂度运算器件实现的基础上,由FPGA纯硬件逻辑进行实现,且其实现效果可较好地在显示器上显示,这在未来嵌入式系统的算法实现方面有着重要意义,可逐步将一些复杂度较低的算法放在FPGA上实现,具有较大的灵活性和可移植性。
[1] 郭俊美.基于图像的柱面全景图生成技术研究[D].西安:西安电子科技大学,2009.
[2] 彭红星,宋鸿陟,邹湘军,等.柱面全景图生成技术的研究与实现[J].计算机工程,2010,36(9):208-211.
[3] 涂桂林.基于图像绘制的灰度拼接改进算法及柱面全景图生成技术[D].合肥:合肥工业大学,2007.
[4] 付金红.柱面全景图像拼接算法的研究[D].哈尔滨:哈尔滨理工大学,2005.
[5] 刘晓妮,卢奕南,杨华民,等.基于OpenCV的曲面全景投影算法研究[J].计算机仿真,2011,28(2):272-275,307.
[6] Altera Conpration.External memory interfaces in the cyclone III device family[M].San Jose:Altera Conpration,2009.
[7] Altera Conpration.DDR and DDR2 SDRAM high-performance controller user guide[M].San Jose:Altera Conpration,2009.
[8] Micron.512MDDR2[M].USA:Micron Technology,2004.
Realization of Cylinder Projection Arithmetic Based on FPGA
WU Xiaobing
(School of Engineering,Xidian University,Xi’an 710071,China)
The principle of the cylinder projection arithmetic is introduced.A system design based on hardware logic is presented.The design starts with writing the image data into DDR2 SDRAM,and then realizes the cylinder projection arithmetic with hardware logic on Cyclone III series FPGA produced by Altera company.At the same time it creates a CameraLink schedule which is delivered to the back-end,and then displays the converted data on LCD via DVI interface in real time.The display results on LCD show that the cylinder projection realized by hardware achieves anticipated results.
FPGA;cylinder projection;Cameralink;DDR2 SDRAM
2014- 10- 17
武晓斌(1989—),男,硕士研究生。研究方向:图像处理,FPGA程序设计。E-mail:w13630570960@126.com
10.16180/j.cnki.issn1007-7820.2015.05.003
TN79;TP301.6
A
1007-7820(2015)05-009-04
