基于Ornstein-Uhlenback类模型的最优分红

张 娜，王秀莲

（天津师范大学数学科学学院，天津 300387）

基于Ornstein-Uhlenback类模型的最优分红

张 娜，王秀莲

（天津师范大学数学科学学院，天津 300387）

首先，基于Ornstein-Uhlenback类模型获得了其边界期望折现分红总额满足的二阶微分方程；然后，根据初始资金的不同，求出相应分红总额满足的显示表示；最后，确定了最优分红情况下的分红边界.

Ornstein-Uhlenback类模型；期望折现分红；最优分红

保险公司的分红是指保险公司将实际经营生产的盈余，按一定比例向保单持有人进行分配.最优分红策略是指在公司破产之前使期望折现分红额达到最大的策略.关于分红问题的研究有很多[1-6].文献[2]得出了控制扩散模型下的最优分红为边界分红；文献[3]研究了古典概率模型下，随机观察时间满足Erlang（n）分布的最优分红问题；文献[4]研究了模型U（t）=x+μt+σB（t）的实际性破产和随机观察时间满足指数分布的最优分红.考虑到投资产生的利息会对保险公司的分红产生一定的影响，本研究考虑盈余带利息的Ornstein-Uhlenback类模型在边界分红下的最优分红问题.

1 模型与预备知识

盈余过程{U（t），t≥0}可表示为

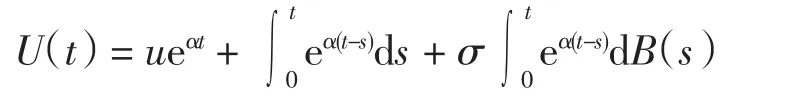
其中：u=U（0）≥0为保险公司的初始资本金；常数c≥0为单位时间内的保费收取量；α为保险公司现有资金产生的利率；σ为扩散系数；{B（t），t≥0}为标准布朗运动，即B（t）～N（0，t）.

该模型可以表示为微分形式：

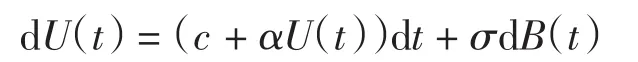
当保险公司盈余为负值时，公司不一定破产，因此，本研究用破产率函数来描述负盈余的破产风险程度，设破产率函数为ω（x）≥0，x≤0.一般情况下，ω（x）是一个非增函数，即盈余x越小，保险公司越容易破产.dt时间内保险公司的破产概率为ω（x）dt+ o（dt）.假设ω（x）与其他的随机变量是独立的.为了最大限度使保险公司盈利，考虑保险公司仅在随机观察时刻分红.设观察时刻是一列独立同分布的随机变量，服从Poisson分布.所以，观察分红的等待时间是独立同分布的随机变量[2]，且它们服从指数分布，均值为1/γ.因此，dt时间内保险公司分红的概率为

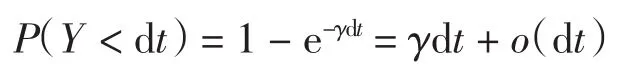
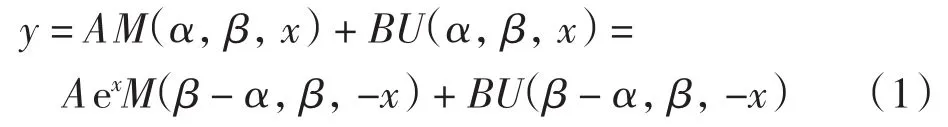
其中：A、B为常数；

2 边界分红策略

给定参数b≥0.如果某一时刻保险公司的盈余大于b并观测到分红，则将超出部分作为分红分给公司股东.设δ＞0为红利折现因子；T为保险公司的实质性破产时刻；D为保险公司在时间[0，T]内的分红总量；V（x，b）为初始资本金为x时D的贴现期望值，即

本研究得到V（x，b）满足以下微分方程：

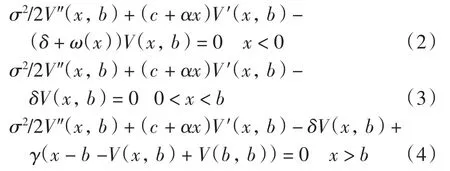
其中：V（x，b）与V′（x，b）是关于x的连续函数，并满足V（-∞，b）=0，当x→∞时，V（x，b）线性有界.

方程（2）～（4）的推导过程如下：

当0＜x＜b时，由于U（t）是关于t的连续函数，所以可以选取充分小的时间dt，使U（t）在（0，dt）时间段内的值不超出（0，b）的范围.由此有

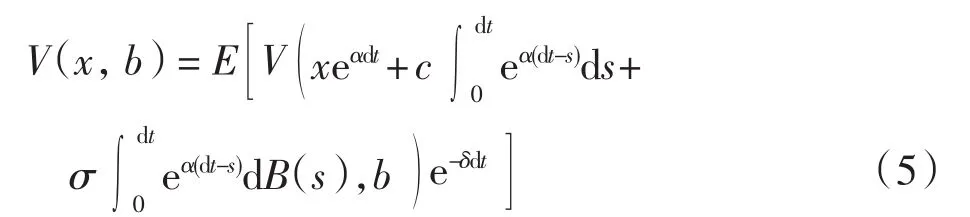
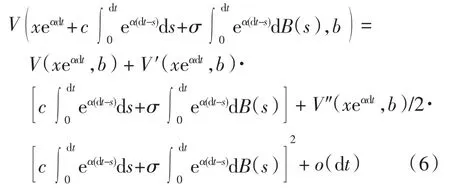
所以有

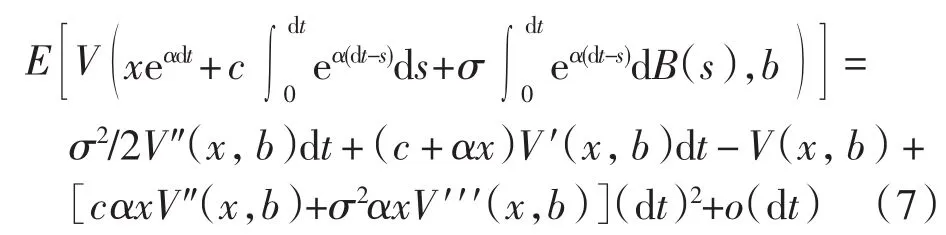
将式（6）和式（7）代入式（5），等式两边同除以dt，并令dt→0，即可得到方程（3）.

当x＞b时，对超出b的部分，若进行观察，则分红，否则不分红.所以有

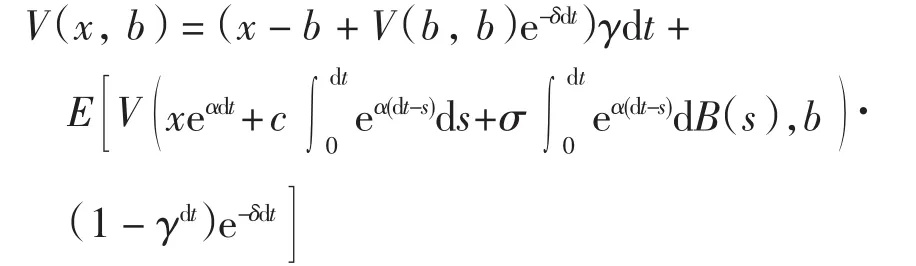
类似方程（3）的计算过程可得方程（4）.

当x＜0时，若破产，则不分红，否则分红.由未破产的概率1-ω（x）dt，可得

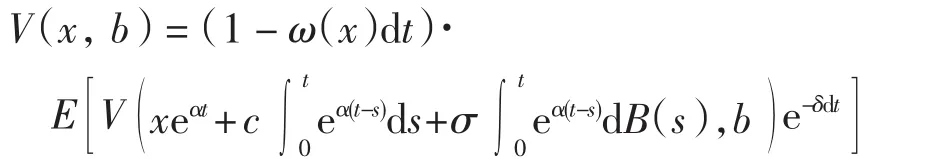
同样，类似前述方法，可得方程（2）.

3 V（x，b）的计算

由于x＞0时，ω（x）=0，所以方程（2）与方程（3）是一致的.方程（4）对应的齐次方程为方程（3），所以首先求解方程（2）.

3.1 ω（x）为常函数的情况

当ω（x）=a时，由方程（2）得

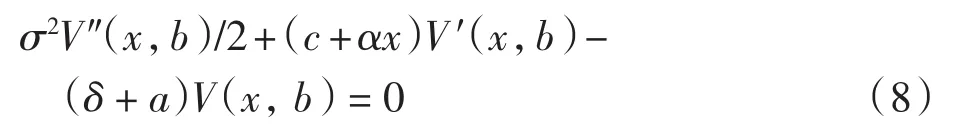
令t=-z2/2，f（z）=g（t），代入上式得Kummer方程

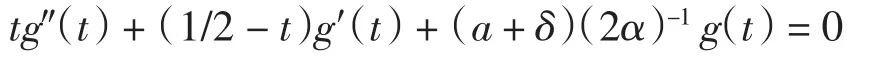
由引理得此方程的解为

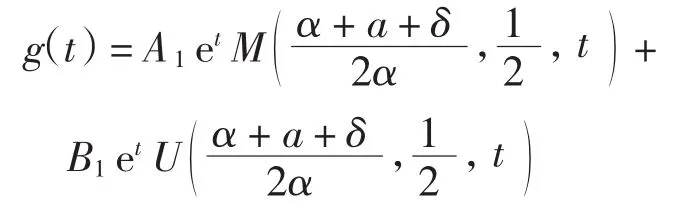
其中A1、B1∈R.由此得

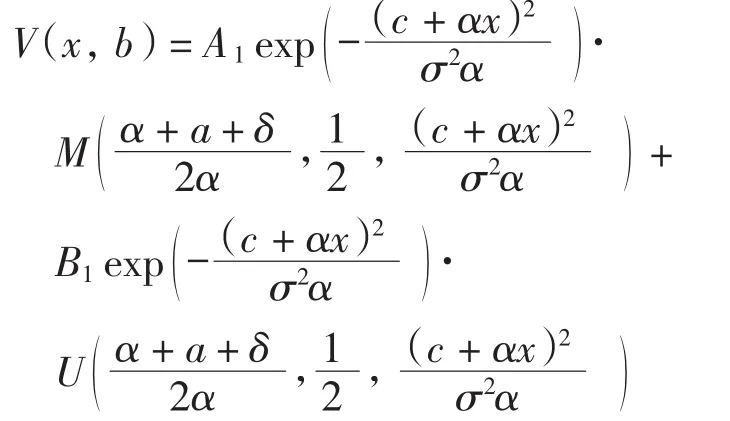
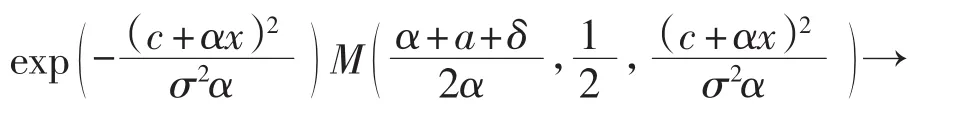
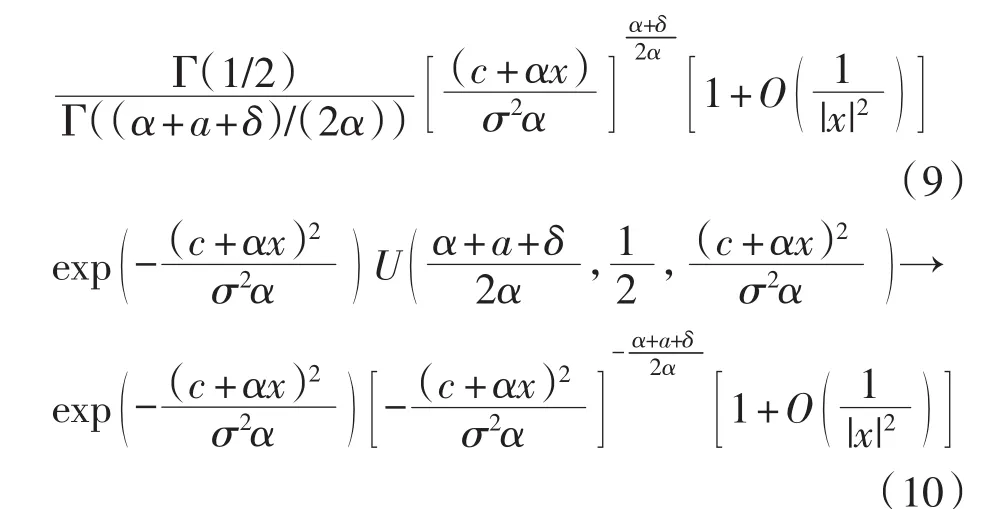
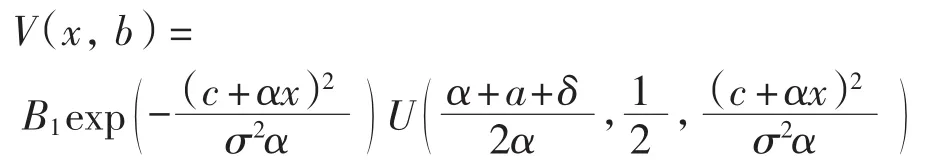
由于V（x，b）在x=0连续，故可设V（0，b）=B1.

3.2 ω（x）为线性函数的情况

当ω（x）=-λx，x＜0时，有

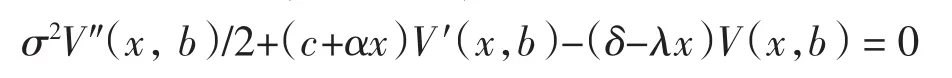
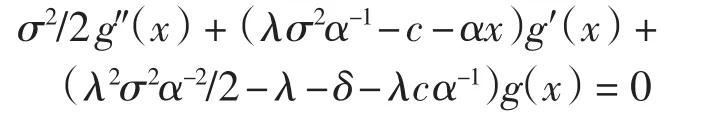
令z=σ-2α-1（c+αx-λσ2α-1）2，f（z）=g（x），代入上式得

则此Kummer方程的解为

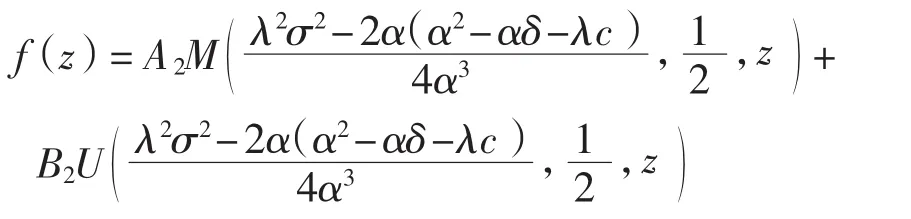
其中A2、B2∈R，则有

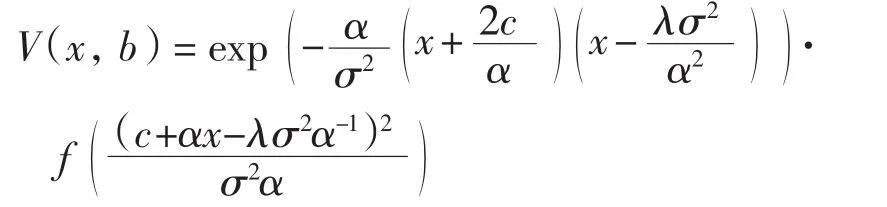
根据V（x，b）在x=0和x=b的连续性，A2、B2可用V（0，b）与V（b，b）表示.

3.3 当0＜x≤b时V（x，b）的计算

当0＜x≤ b时，V（x，b）满足方程（3），由于V（x，b）是关于x和b的二元函数，且V″（x，b）、V′（x，b）与V（x，b）的系数中均不含有b，故设V（x，b）= φ（b）h（x），由方程（3）得h（x）满足

σ2h″（x）/2+（c+αx）h′（x）-δh（x）=0 x≥0（11）且h（x）和h′（x）连续.

在方程（2）的解中，令a=0，得方程（11）的解为

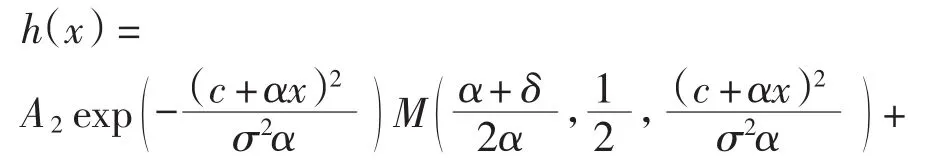
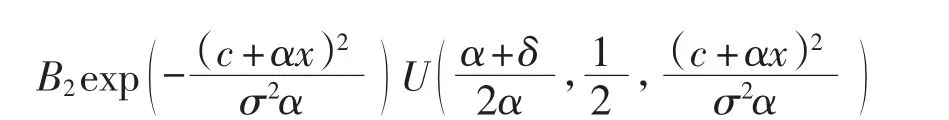
因为h（0）与h′（0）在x=0处连续，所以可用h（0）与h′（0）表示A2、B2.由上式计算得

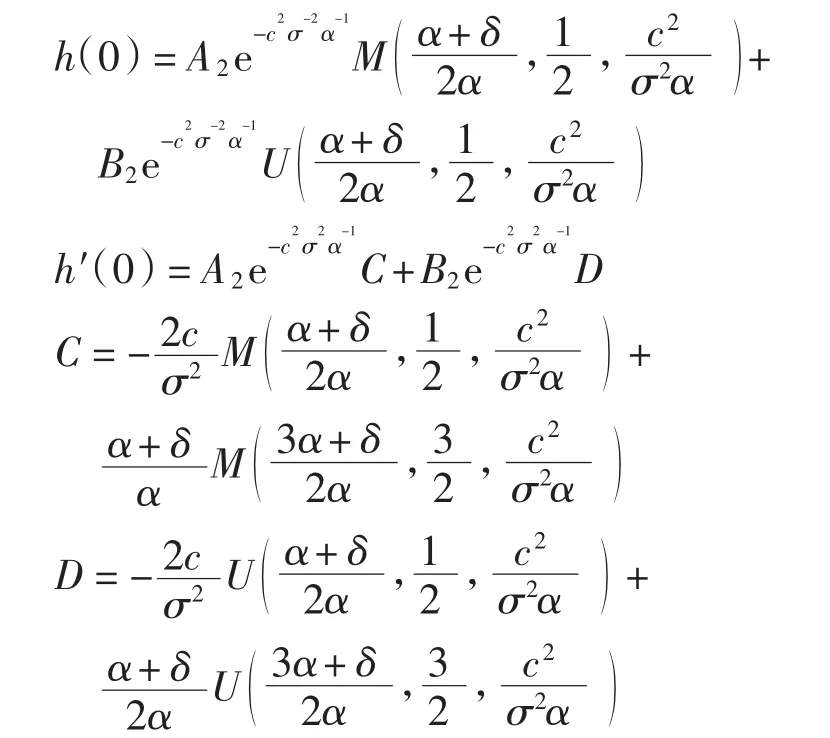
因此A2、B2的表达式为

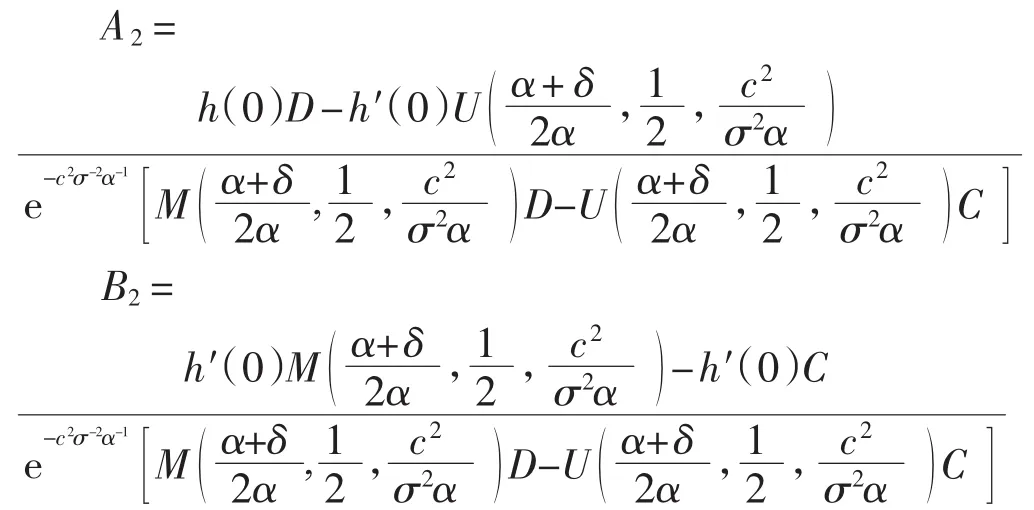
3.4 当x＞b时V（x，b）的计算

当x＞b时，V（x，b）满足方程（4），其对应的齐次微分方程的解为

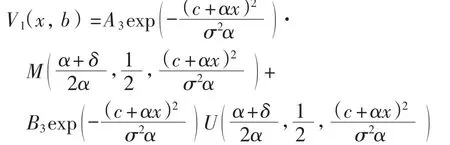
而方程（4）的一个特解为

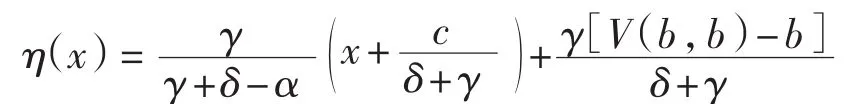
所以，方程（4）的通解为

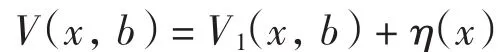
由x→∞时V（x，b）线性有界，得A3=0.即

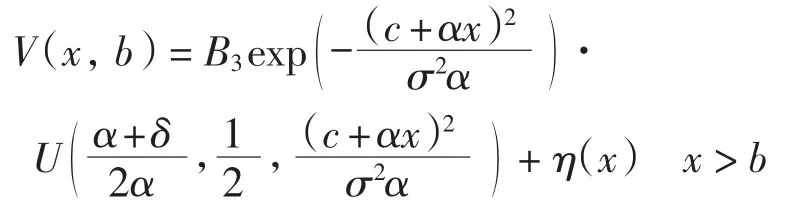
由于V（x，b）在x=b处连续，将x=b代入，得

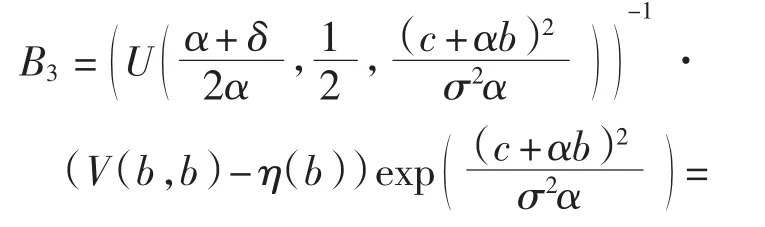
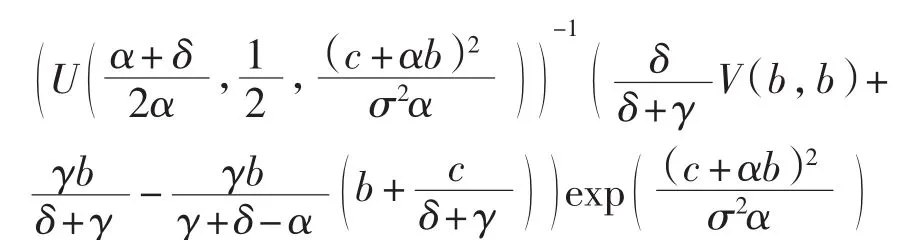
又因为V（b，b）=φ（b）h（b），对V（x，b）关于x求导，并令x=b，有

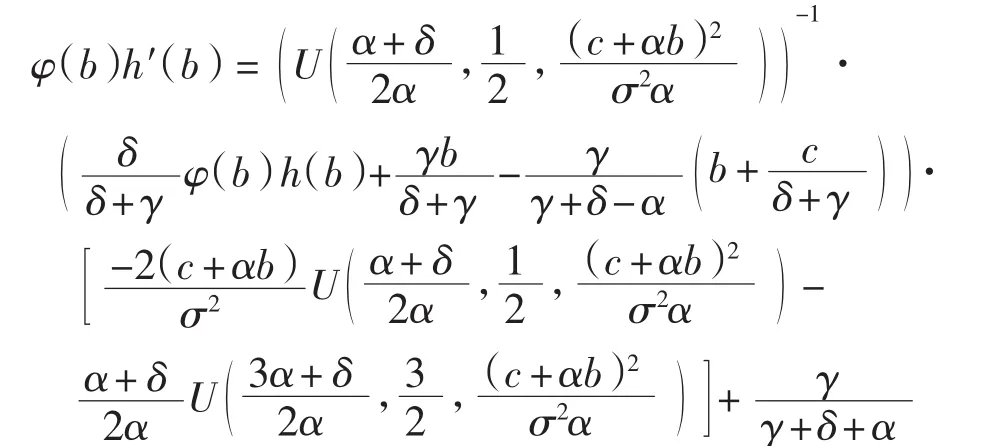
所以

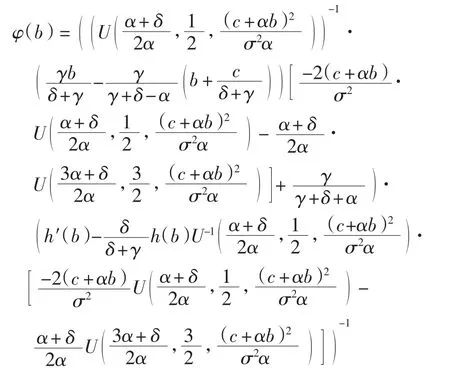
4 最优分红边界的确定

若V（x，b*）=，则称b*为最优分红边界.使V（x，b）最大，即使φ（b）最大.设b*＞0，令φ（b）的导数为0.计算得其中：

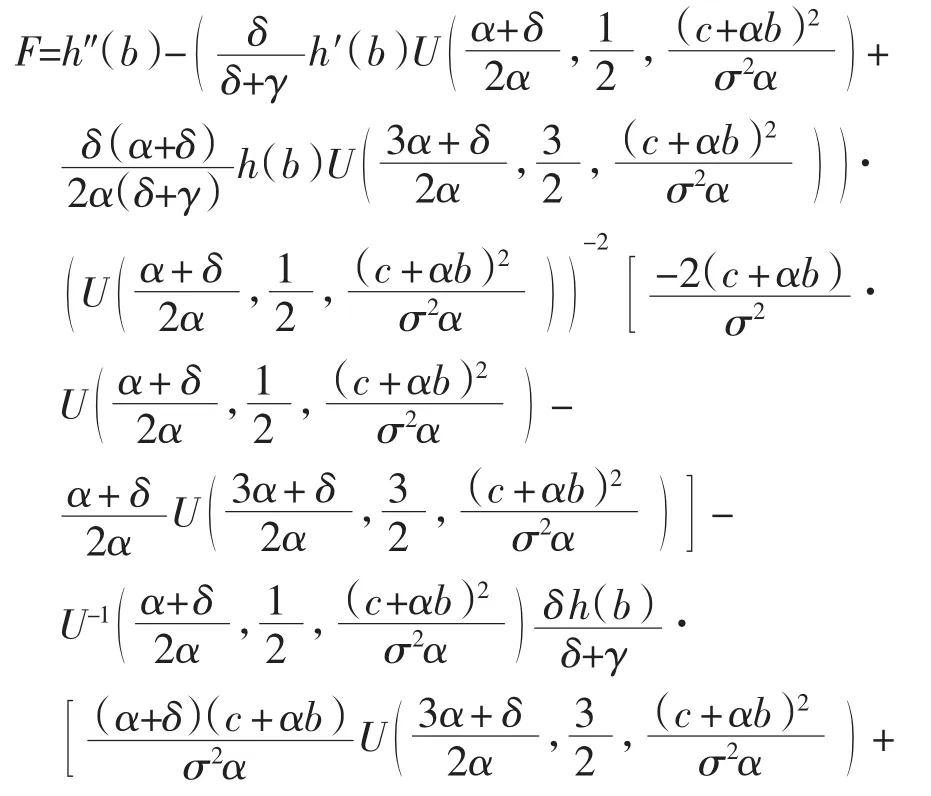
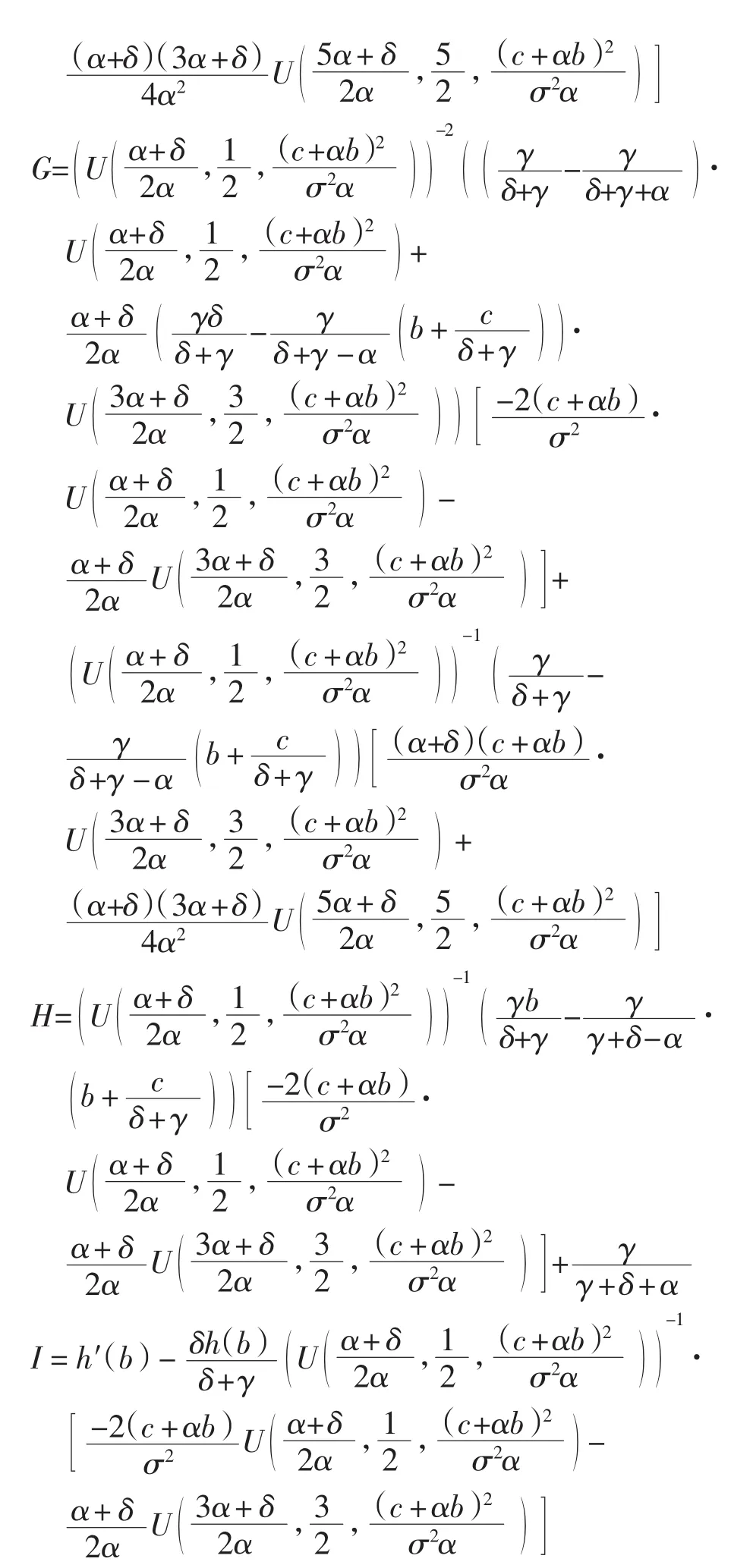
故b*满足GI-FH=0.

[1]王永茂，祁晓玉.基于经典风险模型的最优分红和最优注资[J].郑州大学学报：理学版，2014，46（2）：37-40.

[2]ALBRECHER H，CHEUNG E C，THONHAUSER K.Randomized observation periods for the compound Poisson risk model：dividends[J]. ASTIN Bulletin，2011，41（2）：645-672.

[3] ASMUSSEN S，TAKSAR M.Controlled diffusion models for optimal dividend pay-out[J].Insurance：Mathematics and Economics，1997，20（1）：1-15.

[4]ALBERCHER H，GERBER H U，SHIU E S W.The optimal dividend barrier in the Gamma-Omega model[J].European Actuarial Journal，2011，1（1）：43-56.

[5] 邓丽，谭激扬.复合二项对偶模型的最优分红问题[J].经济数学，2014，31（4）：102-106.

[6]项明寅，危佳钦.具有随机保费风险模型的最优分红策略[J].应用概率统计，2011，27（1）：39-47.

（责任编校 马新光）

Optimal dividend barrier in Ornstein-Uhlenback type model

ZHANG Na，WANG Xiulian
（College of Mathematical Science，Tianjin Normal University，Tianjin 300387，China）

Based on Ornstein-Uhlenback type model，the differential equations of the expected discounted dividends until bankruptcy under a barrier strategy is obtained.In term of the different initial surplus of companies，the explicit expressions of the expected discounted dividends are arrived.Subsequently，the optimal barrier is determined.

Ornstein-Uhlenback type model；expected discounted dividends；optimal dividend barrier

1671-1114（2015）04-0001-04

O211.67

A

2015-03-11

国家自然科学基金资助项目（11401436）；天津师范大学博士基金资助项目（52XB1204）.

张 娜（1990—），女，硕士研究生.

王秀莲（1965—），女，副教授，主要从事随机过程在金融保险中应用方面的研究.