基于混合正则化的最小二乘三维电阻率反演成像
2015-10-17尹洪东杨怀章薛亚茹刘得军
尹洪东,杨怀章,薛亚茹,刘得军
(中国石油大学地球物理与信息工程学院,北京102249)
基于混合正则化的最小二乘三维电阻率反演成像
尹洪东,杨怀章,薛亚茹,刘得军
(中国石油大学地球物理与信息工程学院,北京102249)
基于经典Tikhonov正则化(classical Tikhonov regularization)的最小二乘反演是三维电阻率反演的主要方法。对于电阻率分片连续的地质体,由于光滑反演解的光滑性使得目标区域与背景区域间边界模糊,不能很好地体现异常体的形态信息和位置信息,成像效果不好。将总变分正则化(total variation regularization)与经典Tikhonov正则化结合,提出混合正则化反演方法,通过模型分析比较经典Tikhonov正则化、TV正则化、混合正则化在反演结果上的不同,证明了引入混合正则化约束的最小二乘反演既保持了经典Tikhonov正则化方法解的稳定性,又具有TV正则化方法解的保边缘性,有效地改善了三维电阻率成像效果。最后将混合正则化的反演方法应用到实际工程,验证了该方法的有效性和实用性。
TV正则化;经典Tikhonov正则化;混合正则化;三维电阻率反演
随着电阻率法勘探的不断发展,人们对电阻率反演问题越来越重视。国内外学者对电阻率三维反演问题展开了研究并提出了不同的反演方法,其中Li[1]提出了基于Born近似的直流电法三维反演,对于电阻率变化较大的地质体,此方法的反演精度很低,很难应用于复杂电性结构的反演。Zohdy[2]反演是针对温纳或施伦贝格测深曲线的解释提出的,其原理是通过不断调整初始模型直至模型测深曲线和实际测深曲线之间的拟合误差达到最小,最终的模型参数即为反演结果,实际是一种最小二乘优化反演[2-3]。目前最小二乘反演是主要的三维电阻率反演方法,Sasaki将有限单元法和最小二乘法结合,并且将光滑约束加入到最小二乘反演中,得到了较好的反演结果,奠定了使用有限单元法和最小二乘法进行电阻率反演的基础[4]。黄俊革等[5-8]分别将“体积因子”、电阻率取值范围、空间形态等作为先验信息施加到电阻率三维反演中,极大地改善了三维电阻率反演问题的多解性,提高了深度较大的地质体的分辨能力。吴小平等[9-12]分别在雅克比矩阵的求解、反演方程求解方法等方面对最小二乘反演方法进行了发展和完善,使得三维电阻率反演速度得到了很大的提高、反演效果有了显著进步。相鹏[13]提出了一种改进的预条件非线性共轭梯度法,通过构建形状更接近高斯牛顿Hessian矩阵的预条件算子提高反演精度和计算速度。另外随着计算技术和最优化理论的不断发展,非线性反演方法也被引入到电阻率反演中,如程勃等[14-18]实现了遗传算法、统计学建模法、BP神经网络等优化方法在电阻维反演中的应用。上述的研究工作为三维电阻率反演奠定了基础并且取得了很好的发展和完善,但对于电阻率值分片连续的三维地质体,最小二乘反演解的光滑性使得反演的结果过度光滑,导致目标区域与背景区域边界模糊,不能很好地体现出异常体的形态信息和位置信息,降低了成像的分辨率。为解决上述问题,笔者在最小二乘光滑反演的基础上引入TV正则化方法。TV正则化方法首先由Rudin等提出并应用于图像处理的图像去噪中[19]。由于TV正则化函数可以很好地保持图像的边缘信息,因而在图像重建、地震资料解释等方面有着广泛的应用[20-22],并且已经有学者将TV正则化方法应用到反演中去[23-24],并得到了很好的结果。韩波等[25-26]将TV正则化与经典的Tikhonov正则化的混合正则化方法应用到电阻率二维反演中,大大提高了异常体的成像分辨率。笔者在相关研究的基础上,将混合正则化方法引入到三维电阻率反演中,针对电阻率值分片连续的地质体模型进行算例分析。
1 三维电阻率成像基本原理
1.1数学模型
在直流电法勘探中,将直流电源的两端通过电极向大地供电形成的地下电场可作为稳定的电流场来处理。要计算地下稳定电流场的电势分布则必须从其满足的微分方程和边界条件出发,求解边值问题。三维半空间电阻率的数学模型可以归结为以下方程:
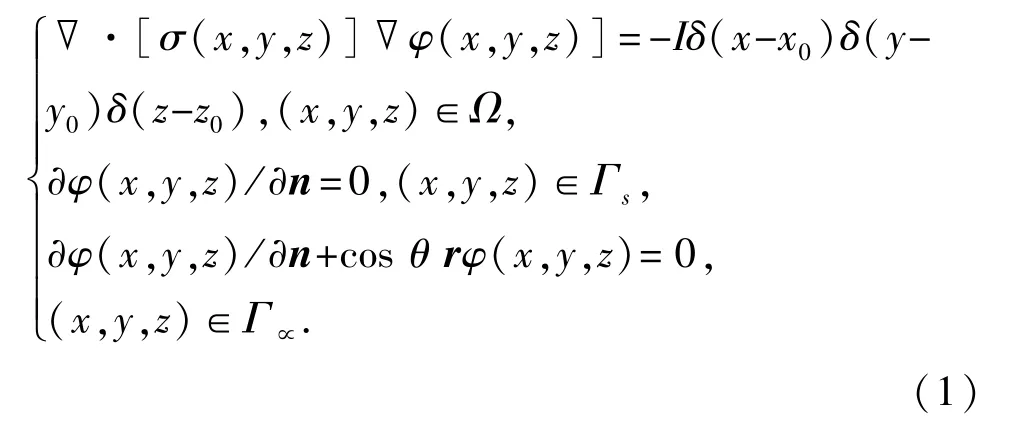
式中,σ为电导率;φ为电势;δ为狄拉克函数;(x0,y0,z0)为源的空间位置;n为边界外法线方向的单位矢量;r为源点到边界点的径向矢量;θ为n和r的夹角;Ω为半空间区域;Γs为半空间区域的地面边界;Γ∝为半空间区域的无穷远边界。
1.2正演方法
考虑到有限体积法兼具有有限单元法和有限差分法的优点,本文中采用有限体积法模拟三维空间内的电阻率分布情况。首先采用单元中心方式的结构网格对三维区域进行离散,为方便起见将方程(1)中第一个方程的右端用s表示:
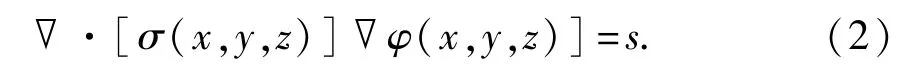
对式(2)进行体积分后得

其中离散电阻率σ=(σ1,σ2,…,σn),n表示有限体积单元的个数。将式(3)离散后得

式中,A为离散正演算子;u为离散电势;q为点源位置矩阵。在实际工作中,只能测量到部分区域(如地表)的电位信息d,所以有

其中Q为投影矩阵。
1.3基于混合正则化的最小二乘反演
1.3.1最小二乘混合正则化反演的目标函数
反演问题是地球物理学中的核心问题,反演的目的是通过地面测量的数据获取地球物理模型。对于三维反演问题,将模型剖分成Nx×Ny×Nz的三维网格,反演要求的参数就是各网格单元内的电阻率值。采用最小二乘光滑反演目标函数可表示为
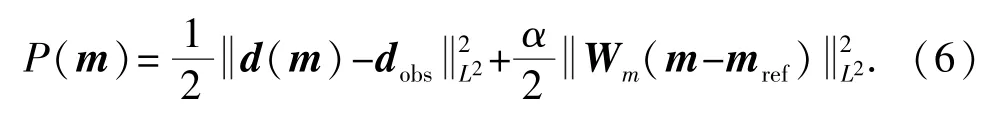
式中,d(m)为给定模型m通过正演得到的数据;dobs为观测数据;α为正则化参数;Wm为光滑度矩阵;mref为参考模型。
相比于最小二乘法的目标函数,该方法加入了经典Tikhonov正则化约束项此约束项减弱了反演问题近似解的不稳定性,使模型参数的变化趋于光滑,最终得到光滑的反演结果。对于电阻率值分片连续的地质体,只采用经典Tikhonov正则化约束的最小二乘光滑反演往往会导致目标区域与背景区域边界模糊,不能保持异常体的边缘,为此将TV正则化方法引入到最小二乘反演中。TV正则化函数如下:

其中D为三维梯度算子矩阵,其作用是使三维模型m中的每一个元素都同其相邻的元素做梯度运算。对于大小为Nx×Ny×Nz的剖分网格,D可以表示为

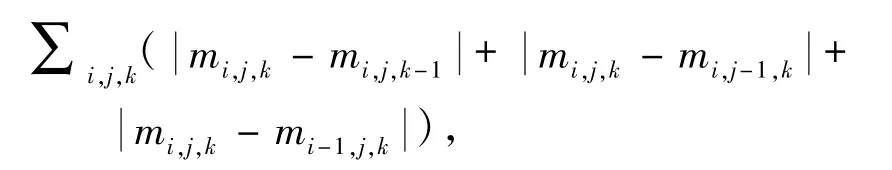
其中,i、j、k表示三维模型中每个单元编号。
通过模型试验发现,由于TV正则化存在解的不稳定性,导致成像时会产生虚假边界。受文献[25]、[26]启发,本文中将经典Tikhonov正则化和TV正则化两种正则化方法结合后应用到最小二乘三维电阻率反演中来,此时目标函数可写为

式中,α、β为正则化参数,两者的值起到调节不同约束项的作用。
1.3.2基于迭代再加权的模型修正量的求解
在最小二乘意义下,反演方程的求解采用了将非线性问题线性化的方法,因此反演必须经过多次迭代来修正模型参数,才能使得估计解^m不断逼近真实解m*。模型参数修正量可以通过迭代再加权方法求解。迭代再加权方法[27]是解无约束优化问题的重要方法,其核心思想是通过计算一系列权系数不断更新的加权最小二乘问题得到目标函数的最优解。求解时首先对目标函数(8)进行转化,采用加权的方式将L1范数松弛为L2范数形式:


设第k次迭代后模型参量为m(k),此时的w=将d(m)、m在m(k)的邻域用泰勒级数展开,并略去二次以上高阶项可以近似为

将式(10)、(11)带入到式(9)中,得

根据多元函数的极值理论,要求解模型修正量δm须对式(12)进行求导运算:
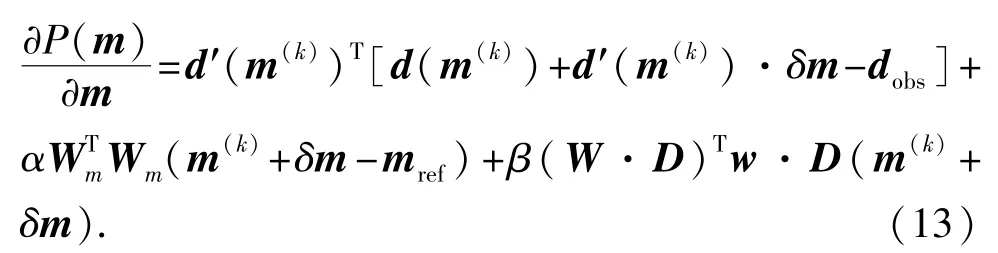
记J=d′(m(k))为偏导数矩阵,Wtv=w·D为再加权矩阵,令,得

这样得出模型修正量为δm=H-1·g。
2 模型试验及分析
为了验证基于混合正则化的最小二乘三维电阻率反演方法兼有经典Tikhonov正则化和TV正则化的优点,利用RESINVM3D共享代码[28]建立了两个模型,合成观测数据开展数值算例研究。两个模型电极排列均采用四极E-SCAN高密度测量方式,其中电流源采用双极供电,共41对,电位测量点93个,共有3813个测量数据。
2.1模型1及其分析
模型1是电阻率为40 Ω·m、大小为34 m×35 m×16 m的均匀半空间中存在两个电导率为200 Ω ·m、大小为6 m×6 m×4 m的高阻异常体,两个异常体并排放置,两个异常体的顶部埋深都为2 m,如图1所示(a)为模型1的水平剖面图,(b)为模型1的x-z垂直剖面图,(c)为模型1异常体所在的目标层的三维剖面图。

图1 模型1剖面图Fig.1 Profiles of model 1
图2为模型1反演结果的目标层剖面图,其中图2(a)是基于经典Tikhonov正则化的光滑反演结果的目标层剖面图,可以看出异常体各层形状均呈椭圆形,且随着深度增加,异常体边缘逐渐扩散,目标区域与背景区域边界模糊,成像的对比度不高;(b)是基于TV正则化反演结果的目标层剖面图,可以看出目标层的第1、2层中异常体的边缘较为清晰,但在第3、4层几乎不能判断出有异常体存在,其原因是TV正则化的保边缘性使得反演过程中能够得到跳跃性较大的参数部分,但是其解的不稳定性造成了异常体的深度判断异常;(c)和(d)分别是TV正则化参数β=0.000 05和β=0.000 01时的混合正则化反演结果的目标层剖面图,相比经典Tikhonov正则化约束和TV正则化约束,反演结果有了很大的改善:一方面目标区域与背景区域边界清晰,能够很好地分辨出异常体的边缘,另一方面异常体内部电阻率值比较一致,能够很好地体现出均匀异常体的特性。由此可以看出:混合正则化既保留了经典Tikhonov正则化解的稳定性和光滑性,又具有TV正则化解的保边缘性。

图2 模型1反演结果目标层剖面图Fig.2 Horizontal planes of target of three inversion results of model 1
图3和图4分别为模型1反演结果在4 m深处的水平剖面图和y=17 m处的垂直剖面图,其中(a)、(b)、(c)、(d)分别是经典Tikhonov光滑反演、TV正则化反演、TV正则化系数β=0.00005和β= 0.00001时的混合正则化反演的结果。从图3(a)和图4(a)中可以清晰地看出:光滑反演使得异常体边缘扩散严重,尤其在纵深方向,几乎不能判断异常体的真实边界。TV正则化的保边缘特性能够在图3(b)中清晰地看出,但由于TV正则化存在对目标区域定位不准确的缺点[26],导致反演的结果中异常体出现重心“上漂”现象[12](图4(b))。图3(c)、图4(c)很好地体现出了混合正则化的优越性:①吸收了TV正则化保边缘特性,相比于经典Tikhonov正则化异常体的边缘扩散现象得到了很好的改善,能够很好地分辨出异常体的边缘;②继承了经典Tikhonov正则化解的稳定性的特点,相比于TV正则化,目标区域定位更准确,异常体中心“上漂”现象消失。
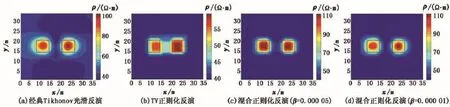
图3 模型1反演结果水平剖面图(z=4 m)Fig.3 Horizontal plane of model 1(z=4 m)
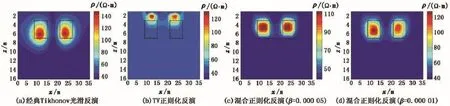
图4 模型1反演结果垂直剖面图(y=17 m)Fig.4 Vertical plane of model 1(y=17 m)
在将两种正则化项进行组合过程中,正则化系数的选取是十分重要的环节,针对模型1在保持经典Tikhonov正则化项的系数α不变的前提下,调节TV正则化项的系数β,经过多次试验得出β的取值范围在0.00001至0.0001之间时得到的结果较为理想:β值大于0.0001时,解会表现出TV正则化解的不稳定性,且β值越大,解就越不稳定;β值小于0.00001时,TV正则化解的保边缘的特性不明显,解的光滑性越来越显著,且β值越小保边缘的特性越不明显。比较图2中(c)和(d)可以看出,β= 0.00005时异常体的边缘更加清晰,β=0.000 01时异常体的边缘和图2(a)更加接近。同样,从图3(c)和(d)、图4(c)和(d)中能够更好地体现出这一结论。
2.2模型2及其分析
模型2是一个大小为34 m×35 m×16 m、电阻率值为200 Ω·m的均匀半空间中存在两个大小为6 m×6 m×4 m的异常体,其中左边蓝色异常体是电阻率为40 Ω·m的低阻体,右边红色异常体是电阻率为400 Ω·m的高阻体,两个异常体并排放置,两个异常体的顶部埋深都为2 m。图5中(a)为模型2的水平剖面图,(b)为模型2的x-z垂直剖面图,(c)为模型2异常体所在的目标层的三维剖面图。
图6为模型2不同方法反演结果的目标层剖面图,其中(a)是基于经典Tikhonov正则化的光滑反演结果的目标层剖面图,(b)是基于TV正则化反演结果的目标层剖面图,(c)、(d)分别是TV正则化参数β=0.00005和β=0.00001时的混合正则化反演结果的目标层剖面图。图7和图8分别为模型2反演结果在4 m深处的水平剖面图和y=17 m处的垂直剖面图,图7和图8中(a)、(b)、(c)、(d)分别是经典Tikhonov光滑反演、TV正则化反演、TV正则化系数β=0.00005和β=0.00001时的混合正则化反演结果。

图5 模型2剖面图Fig.5 Profiles of model 2

图6 模型2反演结果目标层剖面图Fig.6 Horizontal planes of target of three inversion results of model 2

图7 模型2反演结果水平剖面图(z=4 m)Fig.7 Horizontal plane of model 2(z=4 m)

图8 模型2反演结果垂直剖面图(y=17 m)Fig.8 Corss-section of model 2(y=17 m)
从图6(a)中可以看出:经典Tikhonov光滑反演结果中各层高阻异常体电阻率都能够达到350 Ω· m,与模型中高阻异常体电阻率值400 Ω·m十分接近,低阻异常体的电阻率值约为100 Ω·m,与模型中的低阻异常体电阻率值400 Ω·m也较为接近,但是在异常体的边缘方面,无论是高阻异常体还是低阻异常体,其形状都呈椭圆形,这与模型中异常体的形状不符,同样的结果在图7(a)、8(a)中更能够清晰地看出来。造成这种现象的原因是:经典Tikhonov正则化解的光滑性使得电阻率值由高到低过度平滑,不能检测出跳跃性较大的电阻率参数,成像后表现出异常体边缘扩散的现象。图6(b)是TV正则化反演的结果,其中第一层的高阻异常体电阻率约为300 Ω·m,极少数的值在500 Ω·m,其余三层几乎看不出有高阻异常体的存在,低阻异常体也只能在第一、二层明显地看出来,其值约为100 Ω· m,这样的结果在异常体的电阻率值方面与模型较为接近,但是在异常体的位置方面与模型不符,这可能是由TV正则化解的不稳定性造成的,这种不稳定使得反演陷入局部最优;另外,在保持异常体边缘方面,TV正则化反演的结果要好很多,在图6(b)、7(b)中能够清晰地看出低阻异常体为长方形,体现出了TV正则化良好的保边缘性。
同样,在保持系数α不变的前提下,分别设TV正则化项的系数β为0.000 05和0.000 01,将两种正则化项进行结合。从图6、图7、图8的(c)、(d)中可以看出TV正则化系数β越大,TV正则化项的作用体现得越明显;TV正则化系数β越小,TV正则化项的作用越小,经典Tikhonov正则化项越起主导作用。
综合上述两个模型的反演结果可以得出:
(1)异常体边缘信息方面。模型1和模型2中异常体的水平剖面和垂直剖面均为长方形,从反演结果可以看出,经典Tikhonov正则化反演异常体水平剖面和垂直剖面近似为圆形或者椭圆形,并且边缘较为发散;TV正则化反演异常体的水平剖面极为接近长方形,但是垂直剖面形状不规则;混合正则化反演的水平剖面和垂直剖面都非常接近长方形,且异常体边缘较为收敛。由此可见,无论是高阻体还是低阻体,混合正则化约束都能保留异常体边缘信息,而且在刻画异常体边缘信息和减小边界扩散方面要比经典Tikhonov正则化反演有更好的效果。
(2)异常体位置信息方面。从垂直剖面图中可以看出TV正则化反演出现异常体重心“上漂”现象,混合正则化反演要比经典Tikhonov正则化反演得到的异常体的位置信息更为精确。模型1中两个高阻体都位于2~6 m深处,经典Tikhonov正则化反演结果大致位于3~8 m处,混合正则化反演的结果大致位于2~6 m处。模型2中低阻体和高阻体都位于2~6 m处,经典Tikhonov正则化反演中低阻体大致位于2~10 m处,高阻体大致位于3~9 m,混合正则化反演中低阻体大致位于2~6 m深处,高阻体也大致位于2~6m深处。由此看出,混合正则化约束的最小二乘反演方法在体现异常体位置信息方面要比基于经典Tikhonov正则化的最小二乘光滑反演方法更加精确。
(3)数值方面。从两个模型反演结果的剖面图中可以看出,经典Tikhonov正则化反演中异常体的电阻率值比混合正则化约束最小二乘光滑反演更加接近模型的真实值,但是经典Tikhonov正则化反演的结果中产生了假异常,混合正则化反演的结果中则不存在假异常。
3 实际工程应用
在某油田的试验中,以某一试验井的金属套管为供电电极,以1 000 m以外的另一口井的金属套管为回流电极,采用10 KW井地电位发送机发射双极性方波信号,在地下介质中形成一个垂直线电流发射源。以试验井为圆心,以正北方为0°方向,以20°为角度间隔,布置18条长400 m的呈放射状分布的径向测线,测环径向间距为50 m,在径向测线与测环交点处共布置144个测量电极(图9),在试验井附近选择一点作为电位参考点,利用井地电位接收机采集观测井地表各电极的电位差数据。
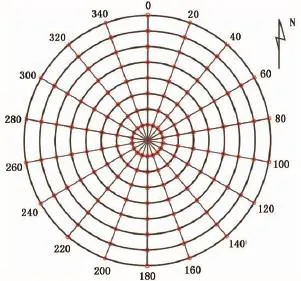
图9 测网布置示意图Fig.9 Sketch map of arrangement of survey network
图10为研究区测量的电位差分布图,通过定性分析图10可以得出,100 m测线电位差相对均匀,在150~400 m测线上300°~0°~80°方向有高电位差异常,说明该范围上存在较大面积的低电阻率分布,相反方向则存在相对高电阻率分布。因此,在远井带的300°~0°~80°方向存在大面积低阻高含水区,其相反方向则为相对高阻区。图11为目标层(800~1000 m)反演的电阻率分布图,其中(a)为经典Tikhonov正则化光滑反演的结果,其定位的低阻区域在270°~0°~140°方向,大大超出了定性分析的结果,(b)为混合正则化反演的结果,其定位的低阻区域在300°~0°~120°方向,相对于经典Tikhonov正则化的反演结果,更接近定性分析的结果。
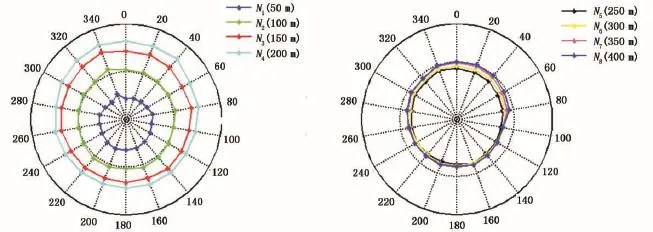
图10 研究区测量的电位差Fig.10 Potential difference of work area
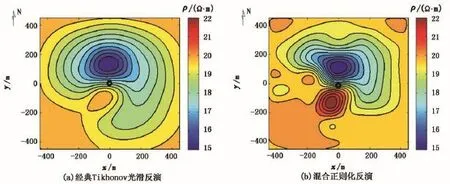
图11 800~1000 m电阻率分布Fig.11 Resistivity distribution at 800-1000 m
4 结束语
将TV正则化约束方法引入到最小二乘电阻率反演中,通过两种正则化的线性组合得到混合正则化的方法。通过对比试验,混合正则化约束的最小二乘反演既保持了经典Tikhonov正则化方法解的稳定性又具有TV正则化方法解的保边缘性,有效地改善了反演中异常体边缘信息与位置信息不精确的问题,从而提高了辨别异常体位置信息与形态的精度,提高了成像的分辨率。在处理实际数据方面,受数据采集的精度和分辨率的影响,该方法只能分辨出大致的电阻率分布趋势,具体的细节还要结合地质资料进行综合分析。
[1] LI Y G,OLDENBURG D W.Approximate inverse mappings in DC resistivity problems[J].Geophysical Journal International,1992,109(2):343-362.
[2] ZOHDY A A R.A new method for the automatic interpretation of schlumberger and wenner sounding curves[J]. Geophysics,1989,54(2):245-253.
[3] 王兴泰,李晓芹.电阻率图像重建的佐迪(Zohdy)反演及其应用效果[J].物探与化探,1996,20(3):228-233. WANG Xingtai,LI Xiaoqin.Resistivity image reconstruction with Zohdy inversion and its application effect[J].Geophysical and Geochemical Exploration,1996,20(3):228-233.
[4] SASAKI Y.3-D resistivity inversion using the finite-element method[J].Geophysics,1994,59(12):1839-1848.
[5] 黄俊革,阮百尧,鲍光淑.有限单元法三维电阻率最小二乘反演中存在问题的研究[J].地质与勘查,2004,40(4):70-75. HUANG Junge,RUAN Baiyao,BAO Guangshu.Re-search on 3D resistivity least-square inversion using the finite element method[J].Geology and Prospecting,2004,40(4):70-75.
[6] 刘斌,李术才,李树忱,等.基于不等式约束的最小二乘法三维电阻率反演及其算法优化[J].地球物理学报,2012,55(1):260-268. LIU Bin,LI Shucai,LI Shuchen,et al.3D electrical resistivity inversion with least-squares method based on inequality constraint and its computation efficiency optimization[J].Chinese Journal of Geophysics,2012,55(1):260-268.
[7] 刘斌,聂利超,李术才,等.三维电阻率空间结构约束反演成像方法[J].岩石力学与工程学报,2012,31(11):2258-2268. LIU Bin,NIE Lichao,LI Shucai,et al.3D electrical resistivity inversion tomography with spatial structural constraint[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(11):2258-2268.
[8] LI S C,NIE L C,LIU B,et al.3D electrical resistivity inversion using prior spatial shape constrains[J].Applied Geophysics,2013,10(4):361-372
[9] 吴小平,徐果明.利用共轭梯度法的电阻率三维反演研究[J].地球物理学报,2000,43(3):420-426. WU Xiaoping,XU Guoming.Study on 3-D resistivity inversion using conjugate gradient method[J].Chinese Journal of Geophysics,2000,43(3):420-426.
[10] 底青云,王妙月.积分法三维电阻率成像[J].地球物理学报,2001,44(6):843-852. DI Qingyun,WANG Miaoyue.3D resistivity tomography by integral method[J].Chinese Journal of Geophysics,2001,44(6):843-852.
[11] ZHANG J,MACKIE R L,MADDEN T R.Three-dimensional resistivity forward modeling and inversion using conjugate gradients[J].Geophysics,1995,60(5):1313-1325.
[12] 屈有恒,张贵宾,赵连锋,等.井地有限线源三维电阻率反演研究[J].地球物理学进展,2007,22(5):1393-1402. QU Youheng,ZHANG Guibin,ZHAO Lianfeng,et al. Study on 3D resistivity inversion for finite surface-borehole line current source[J].Progress in Geophysics,2007,22(5):1393-1402.
[13] 相鹏.一种改进的二维MT预条件非线性共轭梯度反演方法[J].中国石油大学学报:自然科学版,2014,38(4):42-49. XIANG Peng.Two-dimensional MT inversion method based on an improved preconditioned nonlinear conjugate gradient algorithm[J].Journal of China University of Petroleum(Edition of Natural Science),2014,38(4):42-49.
[14] 程勃,底青云.基于遗传算法和统计学的电阻率测深二维反演研究[J].地球物理学进展,2012,27(2):788-795. CHENG Bo,DI Qingyun.2D inversion of resistivity sounding base on GA and statistic method[J].Progress in Geophysics,2012,27(2):788-795.
[15] 程勃,底青云.复杂地电结构条件下统计学建模法电阻率测深二维反演[J].地球物理学报,2014,57(3):961-967. CHENG Bo,DI Qingyun.Statistic modeling 2D VES inversion in complex geo-electric structures[J].Chinese Journal of Geophysics,2014,57(3):961-967.
[16] 徐海浪,吴小平.电阻率二维神经网络反演[J].地球物理学报,2006,49(2):584-589. XU Hailang,WU Xiaoping.2D resistivity inversion using the neural network method[J].Chinese Journal of Geophysics,2006,49(2):584-589.
[17] 刘斌,王传武,杨为民,等.基于并行改进遗传算法的三维电阻率反演方法[J].岩土工程学报,2014,36(7):1252-1261. LIU Bin,WANG Chuanwu,YANG Weimin,et al.3D resistivity inversion using an improved parallel genetic algorithm[J].Chinese Journal of Geotechnical Engineering,2014,36(7):1252-1261.
[18] LIU B,LI S C,NIE L C,et al.3D resistivity inversion using an improved genetic algorithm based on control method of mutation direction[J].Journal of Applied Geophysics,2012,87:1-8.
[19] RUDIN L I,OSHER S,FATEMIE E.Nonlinear total variation based noise removal algorithms[J].Physica D,1992,60(1/4):259-268.
[20] 王化祥,唐磊,闫勇.电容层析成像图像重建的总变差正则化算法[J].仪器仪表学报,2007,28(11):2014-2018. WANG Huaxiang,TANG Lei,YAN Yong.Total variation regularization algorithm for electrical capacitance tomography[J].Chinese Journal of Scientific Instrument,2007,28(11):2014-2018.
[21] 刘志文,潘晓露,李一民.L1范数的TV正则化超分辨率图像重建[J].微处理机,2012(3):37-39. LIU Zhiwen,PAN Xiaolu,LI Yimin.L1 norm of total variation regularization based super resolution reconstruction for images[J].Microprocessors,2012(3):37-39.
[22] 范文茹,王化祥,郝魁红.基于两步迭代TV正则化的电阻抗图像重建算法[J].仪器仪表学报,2012,33(3):625-630. FAN Wenru,WANG Huaxiang,HAO Kuihong.Twostep iterative TV regularization algorithm for image reconstruction of electrical impedance tomography[J]. Chinese Journal of Scientific Instrument,2012,33(3):625-630.
[23] YUAN S Y,WANG S X,LI G F.Random noise reduction using Bayesian inversion[J].Journal of Geophysics and Engineering,2012,9(1):60-68.
[24] ANAGAW A Y,SACCHI D M.Edge-preserving seismic imaging using the total variation method[J].Journal of Geophysics and Engineering,2012,9(1):138-146.
[25] 韩波,窦以鑫,丁亮.电阻率成像的混合正则化反演算法[J].地球物理学报,2012,55(3):970-980. HAN Bo,DOU Yixin,DING Liang.Electrical resistivity tomography by using a hybrid regularization[J].Chinese Journal of Geophysics,2012,55(3):970-980.
[26] 岳建惠.电阻率成像反问题的混合正则化方法研究[D]大连:大连海事大学数学系,2012. YUE Jianhui.Research of mixture regularization methods for EIT inverse problem[D].Dalian:Department of Mathematics,Dalian Maritime University,2012.
[27] 袁义明,孙晨,杨长春.基于迭代再加权最小二乘的地震资料稀疏反演方法[J].地球物理学进展,2013,28(5):2536-2546. YUAN Yiming,SUN Chen,YANG Changchun.Seismic data sparse inversion method based on iterative reweighted technique[J].Progress in Geophysics,2013,28(5):2536-2546.
[28] PIDLISECKY A,HABER E,KNIGHT R.RESINVM3D:a 3D resistivity inversion package[J].Geophysics,2007,72(2):H1-H10.
(编辑 修荣荣)
Least square method based on hybrid regularization for 3D resistivity inversion imaging
YIN Hongdong,YANG Huaizhang,XUE Yaru,LIU Dejun
(College of Geophysics and Information Engineering in China University of Petroleum,Beijing 102249,China)
The smooth least-squares method based on the classical Tikhonov regularization method is the main method in 3D resistivity inversion.For the geological body whose resistivity is piecewise continuous,this method however fails to distinguish the target area from the background due to the smooth nature of the solution.In order to solve this problem,the classical Tikhonov regularization and the total variation regularization(TV regularization)were combined and introduced into the least squares inversion method.Three inversion results based on classical Tikhonov regularization,total variation regularization and the new hybrid regularization were compared.It is shown that the least square method based on hybrid regularization retains both the stability of the classical Tikhonov regularization and the edge-protected property of the total variation regularization.The improvement in 3D resistivity mapping is immediate,and then the method is further verified in practical engineering problems.
total variation regularization;classical Tikhonov regularization;hybrid regularization;3D electrical resistivity inversion
P 631
A
1673-5005(2015)05-0072-10
10.3969/j.issn.1673-5005.2015.05.010
2014-11-25
国家自然科学基金项目(41374151)
尹洪东(1963-),男,副教授,博士,研究方向为油田信号检测、勘探技术及仪器设备的研发。E-mail:yhz1305@163.com。
引用格式:尹洪东,杨怀章,薛亚茹,等.基于混合正则化的最小二乘三维电阻率反演成像[J].中国石油大学学报:自然科学版,2015,39(5):72-81.
YIN Hongdong,YANG Huaizhang,XUE Yaru,et al.Least square method based on hybrid regularization for 3D resistivity inversion imaging[J].Journal of China University of Petroleum(Edition of Natural Science),2015,39(5):72-81.
