基于分区的关联规则Apriori算法研究
2015-10-14李婷张继周
李婷 张继周
【摘 要】Apriori算法是挖掘频繁项集的一种重要方法,但是如果事务数据库大到难以一次装入内存就会遇到瓶颈。本文给出一种基于分区技术的改进算法,通过将大的事务数据库划分为小的分区来实现频繁项集的挖掘。
【关键词】关联规则;Apriori算法;频繁项集;分区技术
【Abstract】Apriori algorithm is an important ways on mining frequent itemsets, but the situation is difficult to handle if the transaction database is very huge. An improving algorithm based on partitioning is given, and the frequent itemsets are obtained by dividing the huge database into small ones.
【Key words】Association rules; Apriori algorithm; Frequent item sets; Partition technique
0 引言
挖掘频繁模式是数据挖掘中的一个重要内容,它是研究如何可以找到频繁出现在数据集中的模式。它对于挖掘数据之间的相关和关联性以及发现频繁模式起着非常重要的作用。因此,频繁模式的挖掘成为了数据挖掘任务和数据挖掘研究关注的重要主题之一[1]。
1 基本概念
(1)项集:由若干个项组成的集合,设I={I1,I2,…,Im},I是一个项集。
(2)k项集:项集中的元素如果有k个,就称这个项集为k项集。
(3)关联规则:设A和B为两个项集,A?奂I,B?奂I且A∩B=Φ,则有关联规则R:A=>B。
(4)支持度(相对支持度):D中事务包含A∪B的百分比,也就是概率P(A∪B)。
(5)置信度:D中事务即包含A同时也包含B的百分比,也就是条件概率P(B|A)。
(6)支持度计数(绝对支持度):包含项集的事务数。
(7)强关联规则:满足最小支持度和最小置信度的关联规则[2]。
(8)关联规则的产生步骤:首先找出所有的频繁项集,然后由频集产生强关联规则。
2 频繁项集挖掘的Apriori算法
关联规则产生的一个步骤就是要找出所有的频繁项集,而这一步是挖掘过程中最重要的,它的开销远远大于第二个步骤,因此它的性能的好坏就决定了整体挖掘性能的好坏。Apriori算法是为挖掘布尔类型关联规则频集的原创性算法。它是一种逐层搜索的迭代方法,其中k项集用于探索(k+1)项集。首先,通过扫描数据库,找出事务中包含的所有项,同时对每一项进行计数,得到候选1项集(C1),用每个计数和最小支持度计数进行比较,得到频繁1项集(L1)。然后,使用L1通过自身的连接产生C2,通过对C2计数找出集合L2。再使用相同的方法找出L3,依次如此做下去,直到不能再找到频繁k项集。
为了提高频集逐层产生的效率,可以使用先验性质来压缩搜索空间。
先验性质:频繁项集的所有非空子集也一定是频繁的。
证明:令S是一个频集,min_sup是最小支持度,D为事务数据库的集合,|D|为D中的事务数,则support_count(S)=min_supX|D|。令S为S的任意一个非空子集,则任何包含项集S的事务必然会包含项集S。因此,support_count(S)support_count(S)=min_supX|D|,故S也是一个频集。
因此在生成候选k-项集之前,可以使用上述性质来进行剪枝,这样可以减去大量的k-项集,从而大大压缩了候选k-项集。
3 基于分区的算法改进
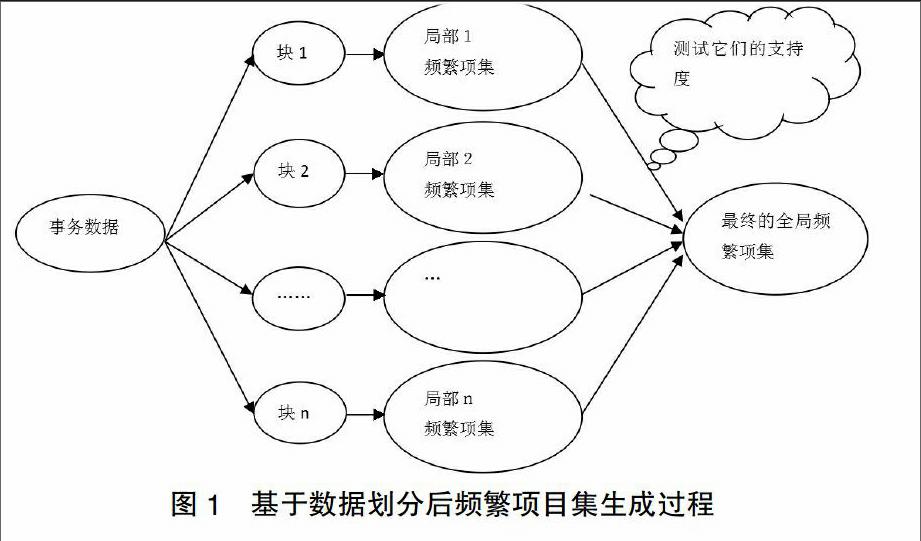
事务数据库有时候会很大而无法一次全部装入内存,此时可以进行事务数据库的划分。分区的大小和分区的数目要使得每个分区都能够放入内存。过程如图所示:
首先,把D中的事务划分成n个非重叠的分区,如果D中事务的最小相对支持度阈值为min_sup,则每个分区的最小支持度计数为min_supX该分区的事务数。对于每个分区,扫描数据库,找出所有的局部频繁项集[3]。局部频集可能是也可能不是整个数据库D的频集。然而,D的任何频集必须作为局部频集至少出现在一个分区中,证明如下:
证明:反证法。假设频集在D的任何一个分区都不频繁。令F为任意一个频集,D为事务数据库集合,C为D中的事务总数,A为D中包含F的事务总数,min_sup为最小支持度。因为F是一个频集,所以A=CXmin_sup。将D分成n个不重叠的分区:d1,d2,d3,…,dn,令C1,C2,C3,…,Cn为分区d1,d2,d3,…,dn各自对应的事务数,则C=C1+C2+C3+…+Cn。令a1,a2,a3,…,an为分区d1,d2,d3,…,dn中包含F的事务数,则A=a1+a2+a3+…+an。因此A=a1+a2+a3+…+an=(C1+C2+C3+…+Cn)Xmin_sup。因为前面已经假设F在D中任意一个分区d1,d2,d3,…,dn中都不频繁,则a1 因此,所有局部频集都是D的候选项集,来自所有分区的局部频集作为D的全局候选项集。然后,第二次扫描数据库D,评估每个候选的实际支持度,以确定全局频繁项集。它的优化算法步骤为:(1)把数据库划分成一些模块大小相当的块,记为N块;(2)在每一块内产生一组自己的频繁项集;记为Li;(3)最后合并这些项集生成一个全局候选的频繁项集;(4)在数据库内,计算全局候选的频繁项集的支持度,得到确定的最终的频繁项集。 4 结语 通过上述对基于划分数据库的Apriori算法的描述,可以清楚的知道改进算法与原始的算法思想的异同,也完整体现了改进算法的解题思路和所在优势,它把一个大而复杂的数据库划分成许多小的结构简单的数据库,大大减小了因为候选集呈指数增长的问题,减少了候选集的构造,缩短了时间;减少了不必要候选集生成的个数,节省了内存空间,提高了算法的效率。 【参考文献】 [1]Jiawei Han,Micheline Kamber.数据挖掘概念与技术[M].2版.范明,孟小锋,译.北京:机械工业出版社,2010. [2]王丽珍,周丽华,陈红梅,等.数据仓库与数据挖掘原理及应用[M].北京:科学出版社,2005. [3]王荣福,余丽娜,等.基于划分技术对Apriori算法的改进[J].科技创新导报,2008(12). [责任编辑:汤静]
