多频段典型地表的双站雷达散射回波预测

2015-10-14张元元吴振森曹运华张玉石

电子与信息学报 2015年11期

张元元吴振森曹运华张玉石

多频段典型地表的双站雷达散射回波预测

张元元*①吴振森①曹运华①张玉石②

①(西安电子科技大学物理与光电工程学院西安 710071)②(中国电波传播研究所青岛 266107)

双站雷达在反隐身、超低空防御方面具有独特优势，但双站测量装置较为复杂，地表参数的准确获取工作耗时耗力，且精度难以保证，地表双站雷达散射数据极其匮乏。为解决上述问题，该文以L/S/X/Ku波段裸土、水泥地和粗糙沙地后向散射实测数据为例，忽略地表的精细结构，采用等效面散射模型和遗传算法反演了各地表的等效介电常数和粗糙度参数，获取其等效参数统计特征，实现对地表双站雷达散射回波的预测。结果表明：该等效面散射模型保证了地表的后向和双站散射回波预测精度；地表双站雷达散射回波随入射波频率的增大而增大；随散射角的增大先增大而后减小，并在镜像方向出现最大值；随散射方位角的增大，地表散射回波先减小而后增大，HH极化双站散射回波的最小值一般出现在方位角处，而VV极化双站散射回波的最小值位置随入射角的增大从方位角向小角度方向偏移，并与入射波频率、地表湿度以及粗糙度参数相关，该双站散射特性可用于地表参数的反演以及目标的反隐身研究。

双站地表散射；多波段测量；等效参数反演

1 引言

近年来，随着空间技术的发展，各类地表的雷达回波特性已广泛应用于星载与机载SAR成像[1,2]、伪装以及目标探测中。由于双站雷达的信息量大，在反隐身、反辐射、抗干扰以及超低空突防方面的独特优势，地物杂波的研究工作逐渐由单站散射转向双站发展[3,4]，其中以美国的“警戒和目标指示多基地系统”、“战术双基地雷达验证计划(TBIRD)”以及英国的自适应双基地雷达研究为典型代表，以提高目标的生存能力和探测能力为主要目的。在低空目标的反隐身、超低空防御研究中，必然涉及到地表与目标的复合电磁散射问题，而地表双站散射场的快速准确获取对地物复合散射场的计算至关重要，因此对地表双站雷达散射回波的研究具有重要的应用价值。

过去几十年里，国内外开展了1.5~94.0 GHz多频段地表的散射测量工作，利用基尔霍夫近似法(KA)[5]、微绕法(SPM)[5]和积分方程法(IEM)[6]等粗糙面高频近似方法对裸土散射特性及其湿度反演[7,8]进行了研究，采用矢量辐射传输理论计算了沙地的后向散射回波[9]，对水泥沥青路面是否存在水层、冰层[10]情况做出了预测。但由于双站雷达测量装置较为复杂，测量实验和理论研究主要集中于单站情况。1994年，文献[11]测量了10 GHz粗糙人造表面的双站镜像散射回波。2007年，Nashashibi等人[3]测量了35 GHz裸土的全极化双站散射特性。2012年，Khadhra等人[12]采用双站测量回波反演了裸土的粗糙度和湿度参数。但相比于单站情况，地表双站散射数据极其匮乏。为了解决上述问题，对于自然界无植被覆盖的规则化单纯地表结构，本文提出根据地表多频段后向雷达散射实测数据预测其双站散射回波，以应用于大区域地表的微波遥感和目标探测研究。

实际应用中，由于大区域内地表的多样性，地表参数的测量工作遇到了输入量众多(地表组分、分层深度、湿度、均方根高度、相关长度等)，获取困难以及不准确性等问题[13]。近些年来，为了解决该问题，国外学者对地表等效粗糙度参数的研究表现出了极大的兴趣。1997年，Su等人[14]采用后向散射系数和湿度测量结果校准了地表相关长度，并将其用于反演后续土壤湿度，提高了精度。2002年，Baghdadi等人[15]提出IEM模型的最优相关长度概念，并建立了地表等效相关长度与均方根高度测量结果的经验公式，校准的IEM模型可以对实测数据进行很好的预测。2011年Lievens等人[16]采用IEM方法和水云模型结合L波段SAR实测数据校准了裸土和植被的有效相关长度，并将其用于小麦覆盖区域土壤湿度的反演。而国内外对于地基散射计下四频段联合反演地表的多等效参数研究还未见文献报道。该等效多参数的反演研究可有效地减少地表物理参数和介电参数的测量工作量，并提升散射系数的预测精度。

因此本文从工程应用角度出发，考虑到计算效率和精度等因素，忽略地表的精细结构，采用多频雷达后向散射数据联合获取地表的等效面参数统计特征，创建其等效模型数据库，实现地表双站散射特性的快速、准确预测。文中地表以裸土、水泥路面和沙地为例，将L/S/X/Ku波段各地表散射模型等效为单层指数谱粗糙面散射模型，假设各波段下单一地表的固有参数(等效均方根高度和等效相关长度)相同，但介电常数随频率发生变化，采用遗传算法[17,18]和多频后向散射实测数据，同时反演各地表的等效粗糙度参数和等效介电常数，并实现对地表双站散射特性的快速、准确预测。

2 后向散射特性测量实验

2013年中国电波传播研究所在青岛周边采用车载散射计对L/S/X/Ku波段HH和VV极化状态下的裸土、水泥地和沙地后向散射系数进行了测量。测量系统主要由Agilent 8362B PNA矢量网格分析仪、功率放大器、功分器、衰减器和收发天线组成，其组成框图如图1所示，散射计的主要性能指标见表1。

图1 系统组成框图

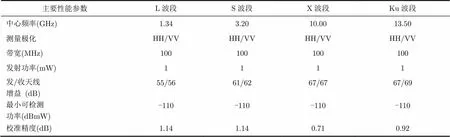
表1 散射计主要参数

实验中将收发天线固定在起重机吊臂上，如图2所示，将天线升至距离地面约14 m高的位置，并通过计算机控制系统改变天线的入射角，其变化范围为0到66，间隔3。每一测试状态下样本数为100，将地表的雷达回波数据记录在电脑中。

如图3所示，本测试采用龙伯球外场定标，将一直径为80 cm左右的标准空心金属球悬挂于地面约14 m高的位置，定标球与天线之间的水平距离取为25 m。将天线照射方向对准金属球进行测量。根据实测金属球后向散射回波的最大值与其散射截面理论解的比值，对测量数据进行定标处理，其定标

图2 地表测量实况图3 外场定标实况

公式可表示为

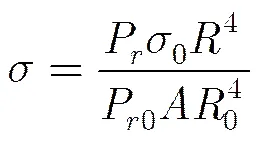
3 等效介电常数和粗糙度参数反演

3.1 等效面散射模型和反演理论

对于自然界无植被覆盖的规则化单纯地表区域，本文采用等效面散射模型来模拟其后向和双站雷达散射回波。由于其包含了地表粗糙度、内部组分以及结构参数变化的影响，地表的等效粗糙度范围较难确定，因此这里选用改进的积分方程法[19](AIEM)作为等效面模型。该方法仅需均方根高度，斜率，可以在较广的粗糙度范围内对地表的雷达散射特征进行预测，其公式为

AIEM模型的输入变量为介电常数、均方根高度和相关长度。此处假设等效均方根高度和相关长度为地表的固有参数，不随频率发生变化，但介电常数因频率的不同而不同。对于裸土、水泥地和沙地表面，分别结合其L/S/X/Ku 4频段实测数据以及指数谱AIEM等效面散射模型，采用最小平方和原理同时反演各地表的等效粗糙度和等效介电常数，其多频段适应度函数为

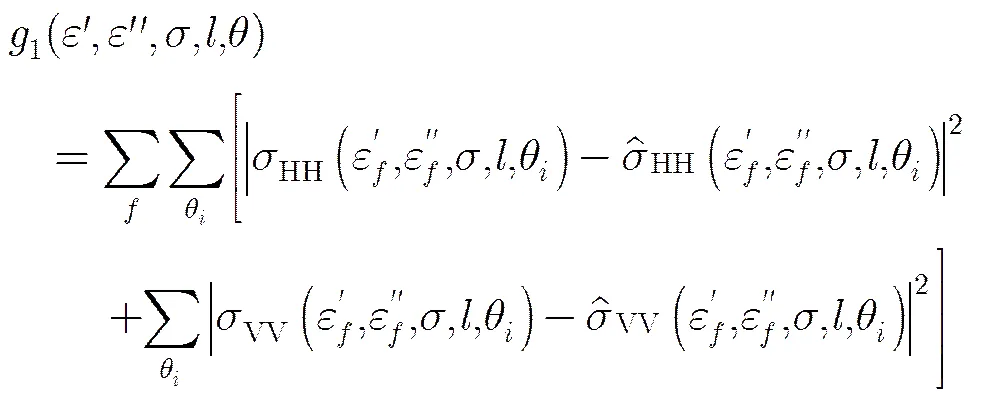
图4 地表后向散射系数实测数据

3.2 等效参数的反演计算

表2 L/S/X/Ku波段地表等效参数的反演结果

4 地表双站雷达散射回波的预测

4.1随入射波频率的变化

根据3.2节裸土、水泥地和沙地的等效介电常数、粗糙度参数的反演结果，分别采用AIEM模型对不同频率下地表的双站雷达散射回波进行预测。从图5中可以看出，随入射波频率的增大，地表粗糙度的电尺寸增大，偏离地表镜反射方向上的双站散射回波也增大，但镜反射方向附近的地表双站散射回波先增大后减小。不同频率下裸土和水泥地的双站散射回波差距较大，但由于沙地表面较为粗糙，其双站散射回波差距最小。图6中，随入射波频率的增大，随散射方位角变化的地表双站散射回波值增大，但沙地的变化情况不明显，VV极化和HH极化地表双站散射回波出现最小值的位置不发生变化，但其数值增大。

4.2随散射角的变化

4.3随散射方位角的变化

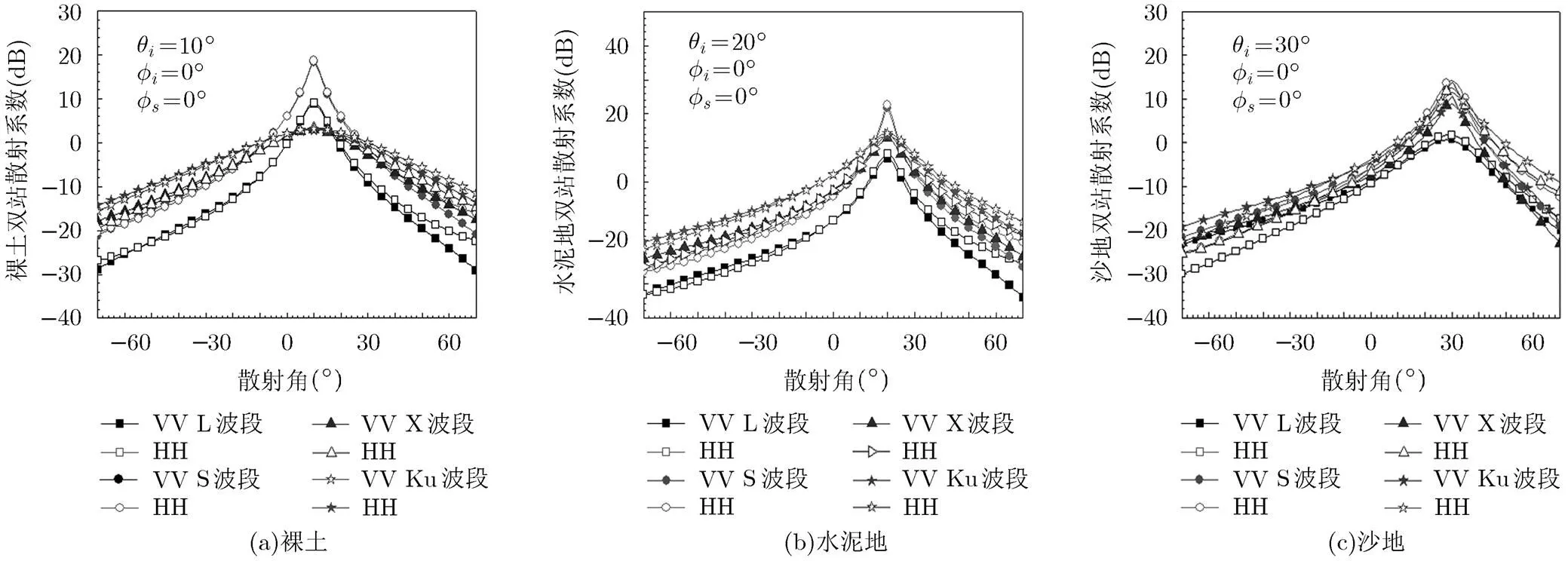
图5 不同频率下，地表双站散射系数随散射角的变化

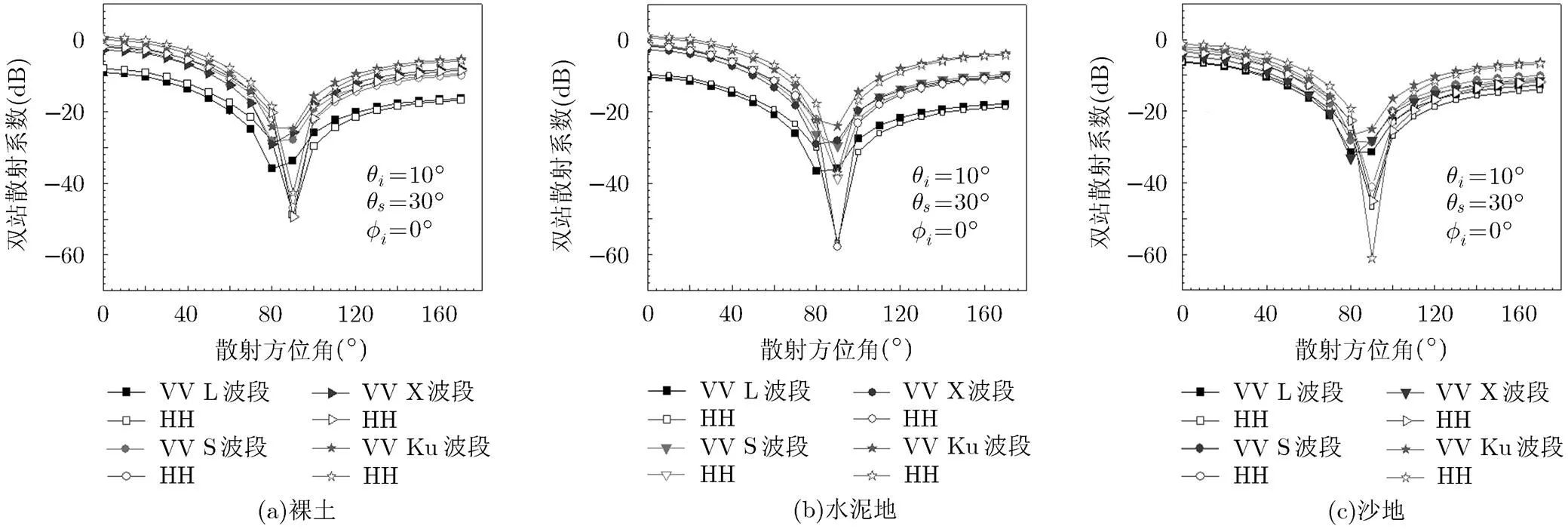
图6 不同频率下，地表双站散射系数随散射方位角的变化

图7 裸土双站散射系数随的变化图8 水泥地双站散射系数随的变化图9 沙地双站散射系数随的变化

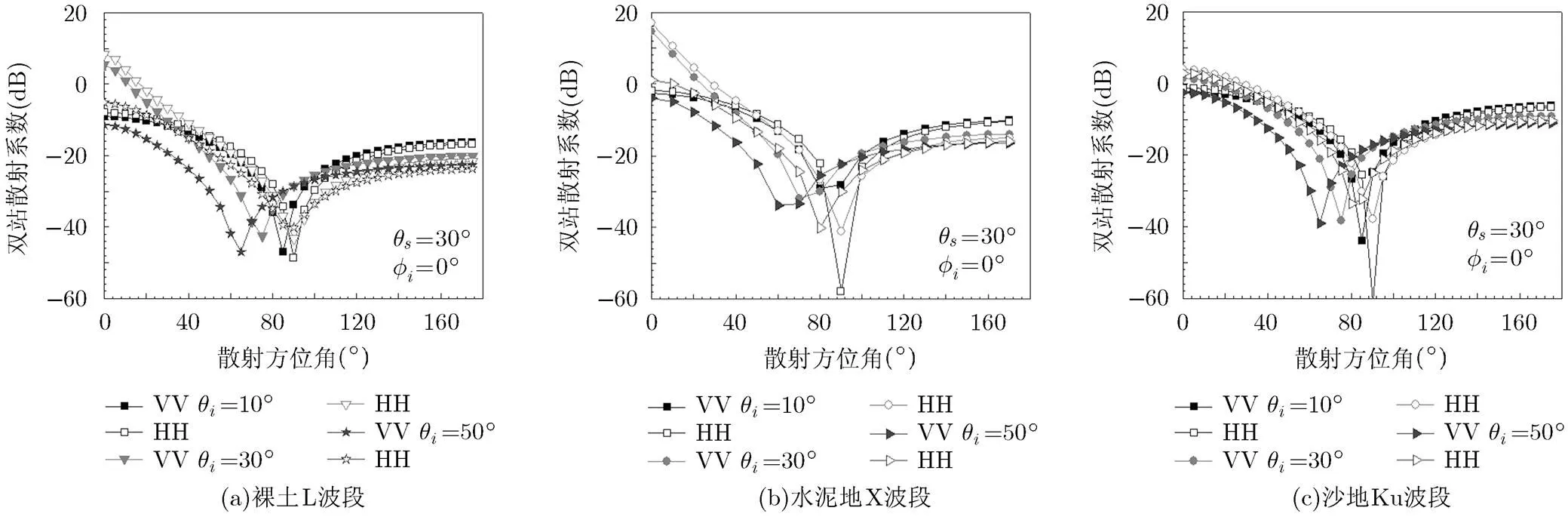
图10 地表双站散射系数随入射角和散射方位角的变化

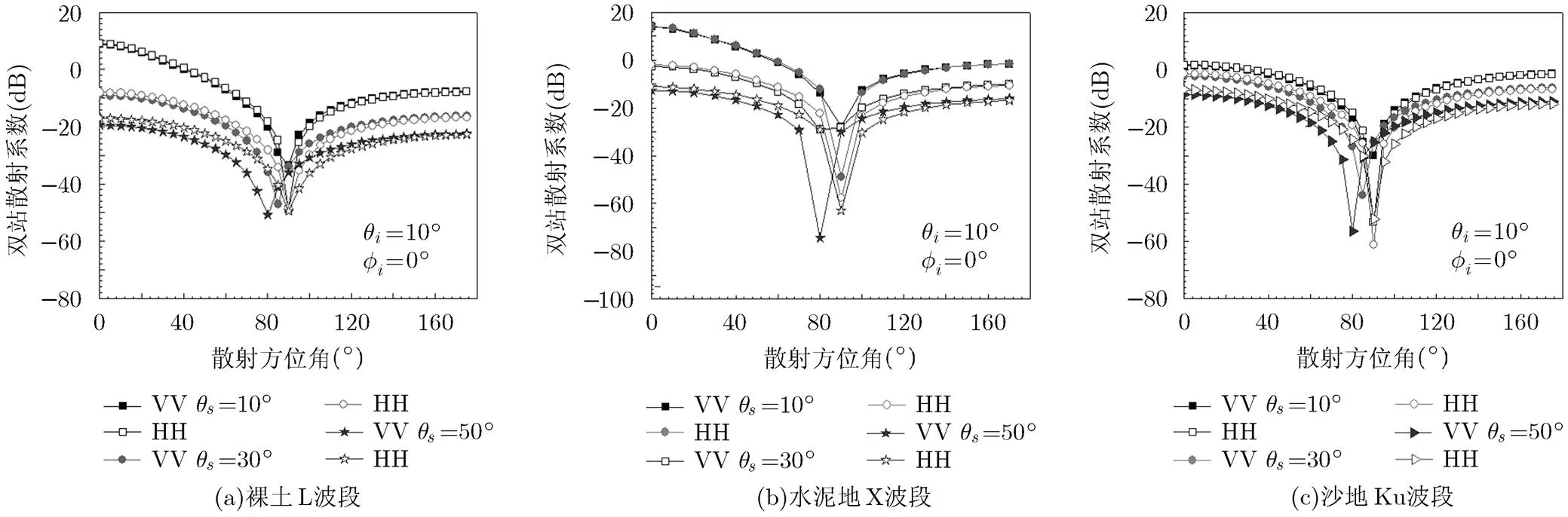
图11 地表双站散射系数随散射角和散射方位角的变化

5 总结

该文从工程应用角度出发，忽略地表的精细结构，建立其等效面电磁散射模型，根据测算融合算法，联合遗传算法和多频地表后向散射实测数据同时反演获取了地表的等效参数统计特征，实现了对地表双站雷达散射回波的预测。该方法适用于自然界无植被覆盖的规则化单纯地表区域，且均方根高度，斜率。地表等效参数对后向雷达散射回波的预测结果与未参与反演运算的实测数据吻合良好，进一步说明等效模型的可行性。对地表双站雷达散射回波的分析可知：VV极化地表雷达散射回波的最小值位置与入射波频率、介电常数以及粗糙度参数相关，可用于地表粗糙度和湿度的反演研究；HH极化地表雷达散射回波的最小值始终处于方位角的位置，此时地表粗糙面的散射作用可以忽略，目标的散射作用凸显，可用于目标的反隐身研究。

相比于单站情况，地表双站雷达散射回波携带了更多的地表信息，其独特优势将使得目标的超低空防御以及反隐身能力得以增强，在星载与机载SAR成像以及地表目标探测中发挥更重要的作用。虽然本文的地表等效电磁模型克服了双站散射数据难以获取的缺点，具有重要的工程应用价值，但地表双站雷达散射回波的预测结果仍需实测数据的进一步验证。

[1] Schlund M, Poncet F V, Hoekman D H,. Importance of bistatic SAR features from TanDEM-X for forest mapping and monitoring[J]., 2014, 151(8): 16-26.

[2] Gupta D K, Kumar P, Mishara V N,. Bistatic measurements for the estimation of Rice crop variables using artifical neural network[J]., 2015(55): 1613-1623.

[3] Nashashibi A Y and Ulaby F T. MMW polarimetric radar bistatic scattering from a random surface[J]., 2007, 45(6): 1743-1755.

[4] Johnson J T and Ouellette J D. Polarization features in bistatic scattering from rough surfaces[J]., 2014, 52(3): 1616-1626.

[5] Ulaby F T, Moore R K, and Fung A K. Microwave Remote Sensing[M]. Massachusetts: Artech House, 1990, Vol. 2, Chapter 11.

[6] Panciera R, Tanase M A, Lowell K,.. Evaluation of IEM, Dubois, and Oh radar backscatter models using airborne L-band SAR[J]., 2014, 52(8): 4966-4979.

[7] 张文吉, 张晓娟, 李芳. 分层土壤后向散射及其在深层土壤湿度探测中的应用[J]. 电子与信息学报, 2008, 30(9): 2107-2110.

Zhang Wen-ji, Zhang Xiao-juan, and Li Fang. Backscattering from multilayer soil and its application to deep soil moisture estimation[J].&, 2008, 30(9): 2107-2110.

[8] Tabatabaeenejad A, Burgin M, Duan X Y,. P-band radar retrieval of subsurface soil moisture profile as a second-order polynomial: first AirMOSS results[J]., 2015, 53(2): 645-658.

[9] Nashashibi A Y, Sarabandi K, Al-Zaid F A,.. An empirical model of volume scattering from dry sand-covered surfaces at millimeter-wave frequencies[J]., 2013, 51(6): 3673-3682.

[10] Sarabandi K, Li E S, and Nashashibi A. Modeling and measurements of scattering from road surfaces at millimeter-wave frequencies[J]., 1997, 45(11): 1679-1688.

[11] De Roo R D and Ulaby F T. Bistatic specular scattering from rough dielectric surfaces[J]., 1994, 42(2): 220-231.

[12] Khadhra K B, Boerner T, Hounam D,. Surface parameter estimation using bistatic polarimetric X-band measurements[J]., 2012, 39: 197-223.

[13] Mattia F, Davidson M, Le T T,. Joint statistical properties of RMS height and correlation length derived from multisite 1-m roughness measurements[J]., 2003, 41(7): 1651-1658.

[14] Su Z, Trochp A, and De Troch F P. Remote sensing of bare surface soil moisture using EMAC/ESAR data[J]., 1997, 18(10): 2105-2124.

[15] Baghdadi N, King C, Chanzy A,. An empirical calibration of the integral equation model based on SAR data, soil moisture and surface roughness measurement over bare soils[J]., 2002, 23(20): 4325-4340.

[16] Lievens H and Verhoest N E C. On the retrieval of soil moisture in wheat fields from L-band SAR based on water cloud modeling, the IEM, and effective roughness parameters [J]., 2011, 8(4): 740-744.

[17] 吕玉增, 刘永祥, 曹敏, 等. 基于遗传算法的一维散射散射中心提取研究[J]. 电子与信息学报, 2006, 28(1): 36-40.

Lü Yu-zeng, Liu Yong-xiang, Cao-min,. 1-D scattering centers extraction technique based on genetic algorithm[J].&, 2006, 28(1): 36-40.

[18] 严韬, 陈建文, 鲍拯. 基于改进遗传算法的天波超视距雷达二维阵列稀疏优化设计[J]. 电子与信息学报, 2014, 36(2): 3014-3020.

Yan Tao, Chen Jian-wen, and Bao Zheng. Optimization design of sparse 2-D arrays for over-the-horizon radar (OTHR) based on improved genetic algorithm[J].&2014, 36(2): 3014-3020.

[19] Wu T D, Chen K S, Shi Jian-cheng,. A study of an AIEM model for bistatic scattering from randomly rough surfaces[J]., 2008, 46(9): 2584-2598.

Multi-band Bistatic Radar Echo Prediction from the Terrian Surfaces

Zhang Yuan-yuan①Wu Zhen-sen①Cao Yun-hua①Zhang Yu-shi②

①(,,’710071,)②(,266107,)

Bistatic radar has an advantage in the anti-stealth and low altitude defense, but the bistatic scattering data measured from the terrian surface are extremely scarce. To solve this problem, the genetic algorithms and the backscattering data from the soil, concrete and the sand surface in L/S/X/Ku band are used to retrieve the effective permittivity and the roughness parameters of the land, and then the bistatic scattering data are predicted. The research above proves that the land equivalent surface scattering model is effective. The bistatic scattering echo increases with frequency, and it first increases and then decreases along with the scattering angles, first decreases and then increases along with the scattering azimuth angles. The minimum value of the bistatic scattering echo always appears in the 90 degree azimuth angles for the HH polarization, and it shifts from 90 degree azimuth angles to the small angle direction for the VV polarization. And also it is related to incident frequency, the moisture and the roughness of land. The bistatic scattering characteristics of land surface can be used for the anti-stealth research and the inversion of the land parameters.

Bistatic land scattering; Multi-band measurement; Equivilent parameters inversion

TN959.71

1009-5896(2015)11-2749-07

10.11999/JEIT150301

2015-03-11；改回日期：2015-06-29；

2015-08-27

张元元 zyy07063@163.com

国家自然科学基金(61172031)

The National Natural Science Foundation of China (61172031)

张元元：女，1986年生，博士生，研究方向为地海面电磁散射以及地表参数的反演.

吴振森：男，1946年生，教授，博士生导师，研究方向为随机介质、非均匀介质中电磁(光)波的传播与散射、目标激光散射特性和电磁散射等.

曹运华：男，1983年生，副教授，研究方向为复杂环境中目标和粗糙面的光散射特性研究.