基于贝叶斯压缩感知的ISAR自聚焦成像

2015-10-14王天云陆新飞陈卫东

电子与信息学报 2015年11期

王天云陆新飞孙麟陈畅陈卫东

基于贝叶斯压缩感知的ISAR自聚焦成像

王天云①②陆新飞①孙麟①陈畅①陈卫东*①

①(中国科学技术大学电磁空间信息重点实验室合肥 230027)②(中国卫星海上测控部江阴 214431)

针对ISAR自聚焦成像，该文提出一种基于贝叶斯压缩感知的高分辨率成像算法。首先利用目标图像的稀疏特性构建级联形式的稀疏先验模型，同时将相位误差建模为均匀分布模型；然后基于最大后验准则，依据贝叶斯压缩感知理论交替迭代求解目标图像和相位误差。与传统稀疏方法相比，所提算法进一步利用了目标图像的联合稀疏信息，将ISAR CS成像转化为MMV联合稀疏优化问题的求解，可以有效改善自聚焦的精度以及成像质量。仿真结果验证了该算法的有效性。

逆合成孔径雷达；自聚焦技术；高分辨成像；贝叶斯压缩感知

1 引言

作为传统高分辨成像雷达的一种重要形式，ISAR可以实现全天候对运动目标进行成像，同时获得距离维和方位维的电磁散射信息[1]。其中距离维分辨能力是由带宽决定；方位维分辨能力是由成像积累转角决定。考虑到实际系统的限制，如发射信号带宽不能太宽，否则会加大数据量并增加硬件实现难度；另外，ISAR目标具有非合作性，获取长相干处理时间(Coherent Processing Interval, CPI)数据需要较高的跟踪精度；加上目标运动状态非平稳且散射特性可能发生较大变化，通常需要复杂的运动补偿，增加了成像难度，因此成像积累转角亦不能太大[2,3]。

在有限带宽和有限转角下，传统ISAR的距离多普勒(Range-Doppler, RD)成像算法由于基于Fourier反演技术，其成像结果通常具有较宽的主瓣和较高的旁瓣，不利于弱小目标的分辨和识别[4]。为了进一步提高ISAR成像效果，近年来，国内外众多学者基于图像稀疏特征，研究了ISAR压缩感知(Compressed Sensing, CS)超分辨成像算法。文献[5,6]分别构建了基于1范数或者加权的1范数约束的稀疏先验模型，获得了较好的成像效果。文献[7,8]则从统计学习角度出发，研究了基于稀疏贝叶斯学习理论的ISAR成像，在噪声和杂波环境中取得了较好估计结果。然而上述文献在信号建模时均基于理想情况下的平动补偿。考虑实际情形，ISAR成像回波方程中不可避免存在平动补偿初相校正后存在的残余相位误差[9,10]，这会使得回波模型中的观测矩阵部分未知，导致回波测量值与观测矩阵之间产生失配现象，将大大减弱传统稀疏重构算法的性能。因此需要研究自聚焦成像技术，降低相位误差对成像结果的影响。经典自聚焦成像方法如PGA[11]和MEM[12]，其本质是基于Fourier重构技术，成像性能提升的空间有限。文献[9,10]则分别研究了存在相位误差情形下的ISAR CS自聚焦成像技术，相比经典自聚焦成像方法具有更好的聚焦精度。其中文献[9]基于确定性反演思想，根据ISAR图像的稀疏特性建立了1范数成像模型，并将相位误差作为模型误差，提出了一种自聚焦成像算法。文献[10]则从贝叶斯压缩感知(BCS)理论出发，选取了Laplace分布的目标先验模型和均匀分布的相位误差模型，利用回波数据进行统计参数估计，以适应ISAR成像的自适应表征，经推导等价于求解基于1范数的稀疏约束优化问题。

以上两种自聚焦成像方法[9,10]仅考虑利用目标图像的稀疏特性。本文在此基础上进一步考虑了目标图像的结构信息，即通过利用图像的联合稀疏先验特征(“行稀疏”和“列稀疏”)，将ISAR CS自聚焦成像转化为多测量矢量(Multiple Measurement Vector, MMV)联合稀疏优化问题的求解，相比传统方法求解单测量矢量(Single Measurement Vector, SMV)优化问题[9,10]，具有更高的参数提取精度[13]。另外本文方法对应的成像模型是基于矩阵形式，能有效地避免传统方法(基于向量表征形式)将目标图像转换成向量模型后引起的2维(距离维和方位维)耦合性，另外还能较好地降低传统CS自聚焦方法的运算复杂度。文中首先将目标图像建模为级联形式的稀疏先验模型[14]，相比传统稀疏先验模型(如1范数约束)，能获得更好地对0范数的近似度，因此可以表征更稀疏的目标特性；与此同时，将相位误差建模为均匀分布模型，并得到相应的MMV优化问题；其次依据最大后验(Maximum, MAP)准则，利用贝叶斯压缩感知理论[15]交替求解目标图像和相位误差，进而获得聚焦之后的ISAR图像。仿真表明，与经典自聚焦方法最小熵(MEM)[12]、基于1范数的自聚焦方法[9]相比，所提方法具有更好的成像性能。

2 信号模型

本文信号建模方式与文献[3,16]类似，假设对雷达原始回波已做过包络对齐处理。根据文献[17]的结论：包络对齐的精度可以实现小于1/2距离单元，但初相校正需要补偿的精度要求在波长量级，因此初相校正之后的残余相位误差通常不能被忽略，此时ISAR回波方程应表示为

将式(2)代入式(1)，经整理得到ISAR回波方程为

进一步考虑噪声因素，并将式(3)对应的ISAR回波方程写成矩阵形式：

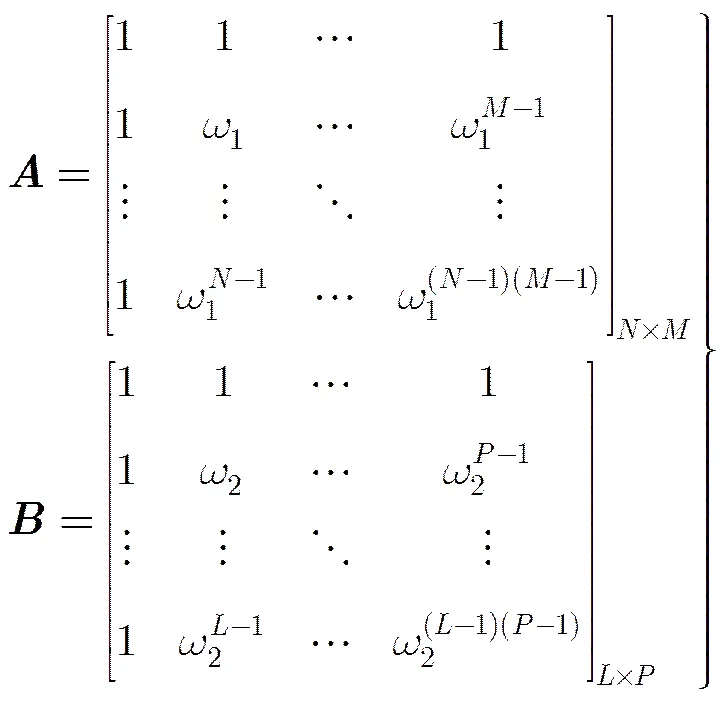
近年来，CS理论利用目标稀疏先验信息，在远低于Nyquist采样速率情形下，只需少量观测样本即可重构原始信号，为获取高分辨率雷达图像提供了一种可行的途径。由于ISAR成像通常是对空或者对海目标(如飞机，导弹，舰船等)，目标散射点在成像空间天然满足稀疏分布，因此本文考虑采用基于CS理论的自聚焦成像技术来提高成像质量。

3 基于贝叶斯压缩感知的ISAR自聚焦成像

3.1 目标参数贝叶斯压缩感知模型

3.1.1目标稀疏模型目前表征目标稀疏先验信息的方式主要包括确定性模型和贝叶斯模型两类。从本质上讲，确定性模型可以利用贝叶斯模型进行等效(即通过选择合适的概率密度函数建立两者的联系)，例如文献[18]阐述了1范数稀疏约束条件在贝叶斯理论体系下的对应关系。与文献[8,9]基于1范数约束不同，本文采用文献[14]中的级联形式的目标稀疏先验模型，具体描述如图2所示。

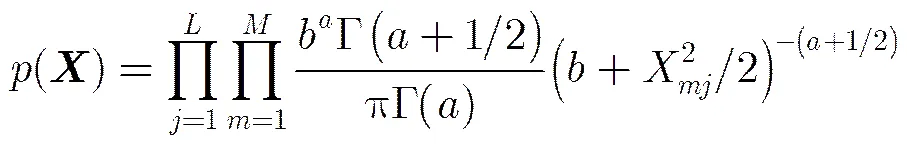
根据文献[14,15]的结论，相比传统稀疏先验模型(如基于1范数约束，对应Laplace分布)，本文利用的级联稀疏先验模型(对应Student-t分布)通常能获得更好的对0范数的近似度，即能表征更稀疏的目标先验信息。另外与文献[14]不同(针对SMV问题，且不考虑相位误差的影响)，本文求解的是含有相位误差的MMV优化问题，因此图2所示的目标稀疏先验模型可看成文献[14]中稀疏模型的拓展。

另外，为了获得高斯分布函数的共轭特性[18]，再假定服从Gamma分布：

图1 ISAR自聚焦成像对应的MMV优化问题示意图

图2 级联形式的目标稀疏先验模型

3.1.3相位误差模型假设相位误差模型服从均匀分布(也可以假定为未知确定参数，不影响后续的结论)，即

3.2 基于贝叶斯压缩感知的ISAR自聚焦成像

结合图2，由式(7)，式(8)，式(10)，式(11)及式(12)，可以得到目标图像、相位误差和噪声功率的倒数等参数对应的联合概率密度函数为

在贝叶斯压缩感知理论框架下，通常是基于MAP准则求解上述未知参数，如式(14)所示。

下面根据式(15)对应的贝叶斯公式，进行目标图像稀疏重构。

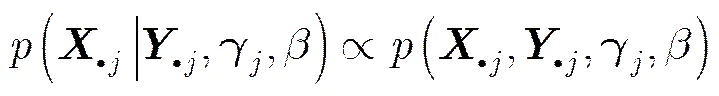
经推导

其中

再根据

将式(19)代入至式(20)，取负对数并略去常数项后，可以得到式(21)所示的优化函数：

注意到：

再结合矩阵求逆公式：

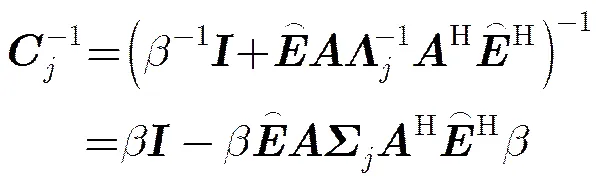
可以得到：

另外，利用矩阵求导的性质：

将式(22)，式(24)，式(25)代入式(21)，根据及得到和，具体求解过程如下：

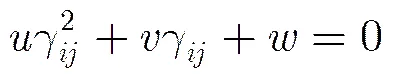
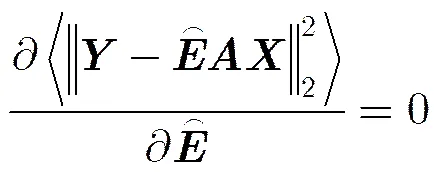
另外，根据式(6)对应的回波方程，不难看出式(33)成立。

通过交替迭代更新步骤(1)和步骤(2)，即能实现对未知变量的迭代求解。由于Type-II最大似然求解方法能保证局部最优解，因此相关参数的估计值随着迭代次数的增加是逐渐减小的。迭代终止的条件为：“循环次数达到预先设定的值”或“相邻两次成像结果不再有较大变化”。

4 仿真结果与分析

下面通过仿真验证所提算法应用于存在相位误差下的ISAR高分辨率成像的有效性。并将成像结果和传统RD成像方法、经典自聚焦方法中的最小熵(MEM)[12]以及基于1范数的自聚焦方法(L1- Based)[9]进行对比，进而阐述本文算法的优越性。

实验数据是基于美国Naval Research Lab提供的MIG25数据，该数据采用频率步进信号，中心频率为9 GHz，带宽为512 MHz，共有512个脉冲序列(对应慢时间)，每个脉冲包含64个脉冲采样(对应快时间)。另外该数据已经过包络对齐和运动补偿处理，且具有较高的信噪比。这里选取了其中前64个脉冲序列和64个脉冲采样作为基础数据进行实验。

实验1 不同SNR情形下各方法的成像结果对比图3是在基础数据中添加随机相位误差和高斯噪声，各方法的成像结果对比，其中随机相位误差幅度浮动在。第1列是RD方法成像结果。由于该方法没有考虑因相位误差引起的回波测量值与观测矩阵的失配现象，所以反演结果最差，并且出现了很多“虚像”；第2列为MEM方法成像结果，可见在SNR较高时，MEM方法具有较好的成像结果，但随着SNR下降，其自聚焦性能有较大程度的恶化；第3列和第4列分别为L1-Based方法和本文方法的自聚焦结果。容易看出，这2种方法在SNR较低时仍具有良好的自聚焦成像能力，但相比而言，本文方法成像效果最好，且几乎没有“虚像”，更利于后续的目标特征提取及识别。这是因为本文方法对目标建立了级联形式的稀疏先验模型，相比基于1范数约束的传统稀疏模型，具有更好的对0范数近似度，可以表征更稀疏的目标信息。另外它基于贝叶斯压缩感知技术，充分利用了“目标、噪声及相位误差”的统计先验信息，在噪声环境中尤其是低SNR情形下具有更好的自适应性和更稳健的参数估计精度。

图3 随机相位误差的幅度浮动在时，各方法在不同SNR下的成像结果

实验2 不同自聚焦成像方法的相位提取精度及成像性能对比定义相位误差提取精度和图像熵分别为

图4 L1-Based方法和本文方法的计算时间对比

表1 3种自聚焦成像方法在图4情形下的相位提取精度及成像性能对比

实验3 不同形式相位误差情形下，所提自聚焦成像方法性能验证实验1和实验2均以随机相位误差作为仿真条件，实验3则给出了基于其他相位误差模式和不同的SNR情形，采用本文方法取得的自聚焦结果对比。图5(a), 5(b)分别是在二次相位误差及正余弦相位误差下的成像结果。可以看出，本文方法在其他相位误差模式下也能获得较好的成像效果，并且在较低SNR下仍然适用。

5 结论

在ISAR图像稀疏特性(即传统稀疏先验信息)的基础上，本文进一步利用了目标图像的结构信息--基于目标图像的“行稀疏”及“列稀疏”特性，将ISAR CS 自聚焦成像转化为MMV优化问题的求解，提出了一种基于贝叶斯压缩感知的成像方法。所提方法充分利用了目标参数、相位误差及噪声模型的统计信息，可以取得较好的成像结果。另外与传统CS自聚焦方法相比，所提方法具有较低的运算复杂度。

图5 本文方法在不同相位误差情形下的成像性能验证

[1] Brisken S and Martella M. Multistatic ISAR autofocus with an image entropy-based technique[J]., 2014, 29(7): 30-36.

[2] Lü Jie-qin, Huang Lei, Shi Yun-mei,.. Inverse synthetic aperture radar imaging via modified smoothed0norm[J]., 2014, 13: 1235-1238.

[3] 吴敏, 邢孟道, 张磊. 基于压缩感知的二维联合超分辨 ISAR 成像算法[J]. 电子与信息学报, 2014, 36(1): 187-193.

Wu Ming, Xing Meng-dao, and Zhang Lei. Two dimensional joint super-resolution ISAR imaging algorithm based on compressive sensing[J].&, 2014, 36(1): 187-193.

[4] Odendaal J W, Barnard E, and Pistorius C W I. Two- dimensional superresolution radar imaging using the MUSIC algorithm[J]., 1994, 42(10): 1386-1391.

[5] Zhang Lei, Xing Meng-dao, Qiu Cheng-wei,.. Achieving higher resolution ISAR imaging with limited pulses via compressed sampling[J]., 2009, 6(3): 567-571.

[6] Rao Wei, Li Gang, Wang Xi-qin,.. Adaptive sparse recovery by parametric weighted1minimization for ISAR imaging of uniformly rotating targets[J]., 2013, 6(2): 942-952.

[7] 成萍, 司锡才, 姜义成, 等. 基于稀疏贝叶斯学习的稀疏信号表示 ISAR 成像方法[J]. 电子学报, 2008, 36(3): 547-550.

Cheng Ping, Si Xi-cai, Jiang Yi-cheng,.. Sparse signal representation ISAR imaging method based on sparse Bayesian learning[J]., 2008, 36(3): 547-550.

[8] Liu Hong-chao, Jiu Bo, Liu Hong-wei,.. Superresolution ISAR imaging based on sparse Bayesian learning[J]., 2014, 52(8): 5005-5013.

[9] Onhon N O and Cetin M. A sparsity-driven approach for joint SAR imaging and phase error correction[J]., 2012, 21(4): 2075-2088.

[10] 徐刚, 包敏, 李亚超, 等. 基于贝叶斯估计的高精度ISAR成像[J]. 系统工程与电子技术, 2011, 33(11): 2382-2388.

Xu Gang, Bao Min, Li Ya-chao,.. High precision ISAR imaging via Bayesian statistics[J]., 2011, 33(11): 2382-2388.

[11] Wahl D E, Eichel P H, Ghiglia D C,.. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]., 1994, 30(3): 827-835.

[12] Li Xi, Liu Guo-sui, and Ni Jin-lin. Autofocusing of ISAR images based on entropy minimization[J]., 1999, 35(4): 1240-1252.

[13] Tzagkarakis G, Achim A, Tsakalides P,.. Joint reconstruction of compressively sensed ultrasound RF echoes by exploiting temporal correlations[C]. Proceedings of the IEEE 10th International Symposium onBiomedical Imaging, San Francisco, 2013: 632-635.

[14] Tipping M E. Sparse Bayesian learning and the relevance vector machine[J]., 2001(1): 211-244.

[15] Babacan S D, Molina R, and Katsaggelos A K. Bayesian compressive sensing using Laplace priors[J]., 2010, 19(1): 53-63.

[16] Du Xiao-yong, Duan Chong-wen, and Hu Wei-dong. Sparse representation based autofocusing technique for ISAR images[J]., 2013, 51(3): 1826-1835.

[17] Chen C C and Andrews H C. Target-motion-induced radar imaging[J]., 1980, AES-16(1): 2-14.

[18] Liu Hong-chao, Jiu Bo, Liu Hong-wei,.. Superresolution ISAR imaging based on sparse Bayesian learning[J]., 2014, 52(8): 5005-5013.

An Autofocus Imaging Method for ISAR Based on Bayesian Compressive Sensing

Wang Tian-yun①②Lu Xin-fei①Sun Lin①Chen Chang①Chen Wei-dong①

①(,,230027,)②(,214431,)

For Inverse Synthetic Aperture Radar (ISAR) autofocus imaging, this paper proposes a high-resolution imaging method based on Bayesian Compressed Sensing (BCS). Firstly, according to the sparsity characteristics of target image, a sparse model with the hierarchical framework is established, which can achieve better approximation to the original0norm. Then, the phase errors are assumed to obey the uniformdistribution. Next, following thecriterion of Maximum(MAP), target image and phase errors are solved using alternate iteration based on BCS theory. Compared with traditional methods, the proposed method further combines the joint sparse information of target image, and converts the ISAR CS imaging into solving a joint Multiple Measurement Vector (MMV) sparse optimization problem, which can improve both the autofocus precision and the imaging quality efficiently. Simulation results show the effectiveness of the proposed method.

Inverse Synthetic Aperture Radar (ISAR); Autofocus technique; High-resolution imaging; Bayesian Compressive Sensing (BCS)

TN958

1009-5896(2015)11-2719-08

10.11999/JEIT150235

2015-02-11；改回日期：2015-06-29；

2015-08-27

陈卫东 wdchen@ustc.edu.cn

国家自然科学基金(61172155, 61401140)；国家863计划(2013AA122903)

The National Natural Science Foundation of China (61172155, 61401140); The National 863 Program of China (2013AA122903)

王天云：男，1986年生，博士生，研究方向为分布式雷达稀疏成像技术、压缩感知.

陆新飞：男，1990年生，博士生，研究方向为高分辨雷达成像、压缩感知.

孙麟：男，1990年生，博士生，研究方向为ISAR成像、阵列信号处理.