非自治动力系统拓扑压变分原理的一点注记

杨将，郭亚晓

(西北大学数学学院，陕西 西安　710127)

非自治动力系统拓扑压变分原理的一点注记

杨将，郭亚晓

(西北大学数学学院，陕西 西安710127)

用类似于非自治熵的变分原理的方法，证明了非自治拓扑压的变分原理的一个不等式，推广了非自治熵的变分原理，丰富了非自治变分原理的内容.

非自治熵；非自治拓扑压；变分原理

1　引言

熵是迄今为止发现的重要的非负不变量，每个紧系统都有一个确定的拓扑熵，它被认为是连续作用在底空间上引起混乱程度的一种度量，而估计和计算紧致系统的拓扑熵就成了动力系统的一个永恒的课题.熵分为测度熵和拓扑熵，因此连接测度熵和拓扑熵的变分原理就显得非常重要.拓扑压是动力系统中拓扑熵的一种推广，也是热力学中的一个重要概念，在热力学的研究中有着重要的意义.因此，压的变分原理无论是在动力系统还是在热力学中都是关注的重点.动力系统又分为自治与非自治，自从自治的熵的变分原理与压的变分原理被证明以后，对变分原理的研究转移到更为广泛的非自治系统的变分原理.2012年朱玉俊在文献[1]中得到了底空间是紧的、映射序列是连续的且保持Borel测度不变的情况下的非自治熵的变分原理，即

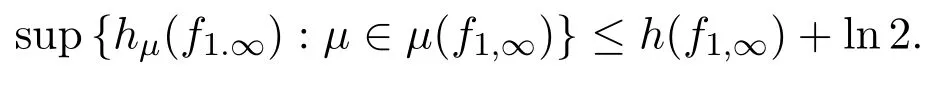
2013年，Jose S.Cánovas在文献[2]中作了进一步的改进，得到了底空间是距离空间且在有限球维数的情况下去掉ln2的变分原理，即

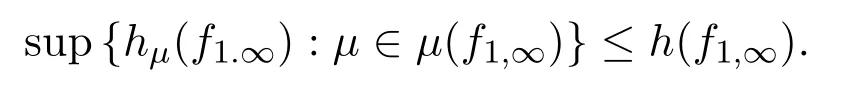
同年Kawan在文献[3]中给出在映射序列等度连续的情况下非自治熵的变分原理的不等式，即测度熵不超过拓扑熵.受这些文章的启发，本文把自治拓扑熵的变分原理进一步推广到非自治拓扑压的变分原理上，并给出一类非自治动力系统拓扑压的变分原理不等式.

2　预备知识

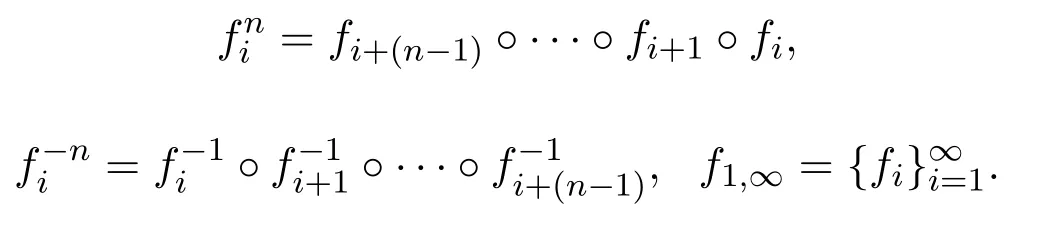
记(X，f1，∞)为非自治动力系统.对于任意的n∈N+，在X上定义新的度量

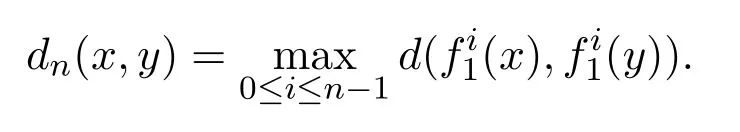
定义2.1[1]设K是X上的紧子集，对任意的ε＞0，称E⊆X为K的(f1，∞，n，ε)生成集，如果对任意的x∈K，存在y∈E，使得dn(x，y)≤ε.

记r(f1，∞，n，ε，K)为K的(f1，∞，n，ε)生成集的最小基数.

定义2.2[2]设K是X上的紧子集，称F⊂K为(f1，∞，n，ε)分离集，如果x，y∈F，xy，则有dn(x，y)＞ε.

同样，记s(f1，∞，n，ε，K)为K的(f1，∞，n，ε)分离集的最大基数.

定义2.3[4]设(X，f1，∞)是非自治动力系统，K是X上的紧子集，定义

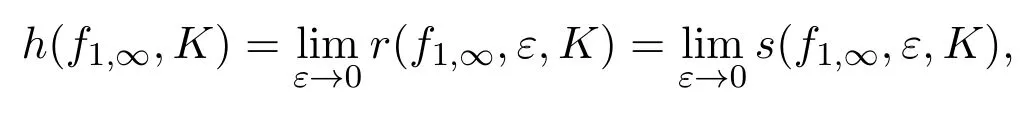
这里

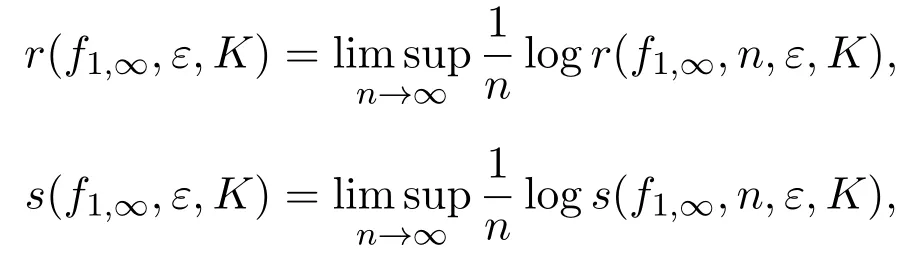
f1，∞的拓扑熵定义为：

有时为了强调度量，记f1，∞的拓扑熵为hd(f1，∞).

设(X，B(X)，m)是概率空间，其中B(X)是Borel可测集的全体，为保测变换，即任意的i∈N+，

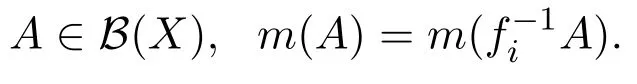
如果对所有的fi，i∈N+，fi保持相同的概率测度m，则称f1，∞保持m，或m是f1，∞的不变测度，并且记X上的所有保持f1，∞测度不变的全体集合为M(X，f1，∞)，现在给出(X，f1，∞)的测度熵的定义.

定义2.4[4]设(X，B(X)，m)是概率空间，m∈M(X，f1，∞)，ξ是X的一个有限可测分解，定义f1，∞相对于ξ的测度熵为：

定义2.5[5]对任意ε＞0，n≥1，φ∈C(X，R)，记

3　主要结果及其证明

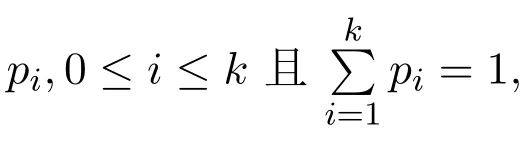
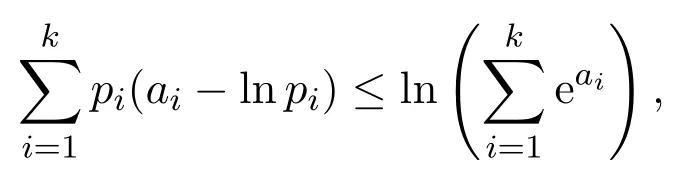
等号成立的充分必要条件为：

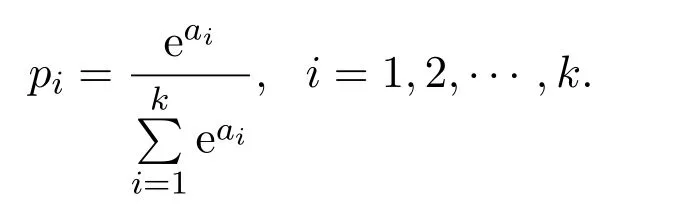
定理3.1设X是紧的度量空间，f1，∞是X上的连续自映射序列，则对任意µ∈M(X，f1，∞)，φ∈C(X，R)，有

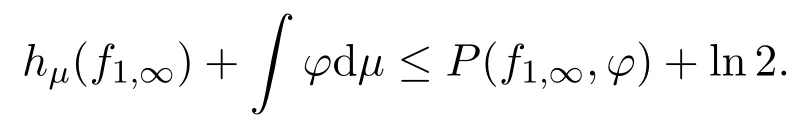
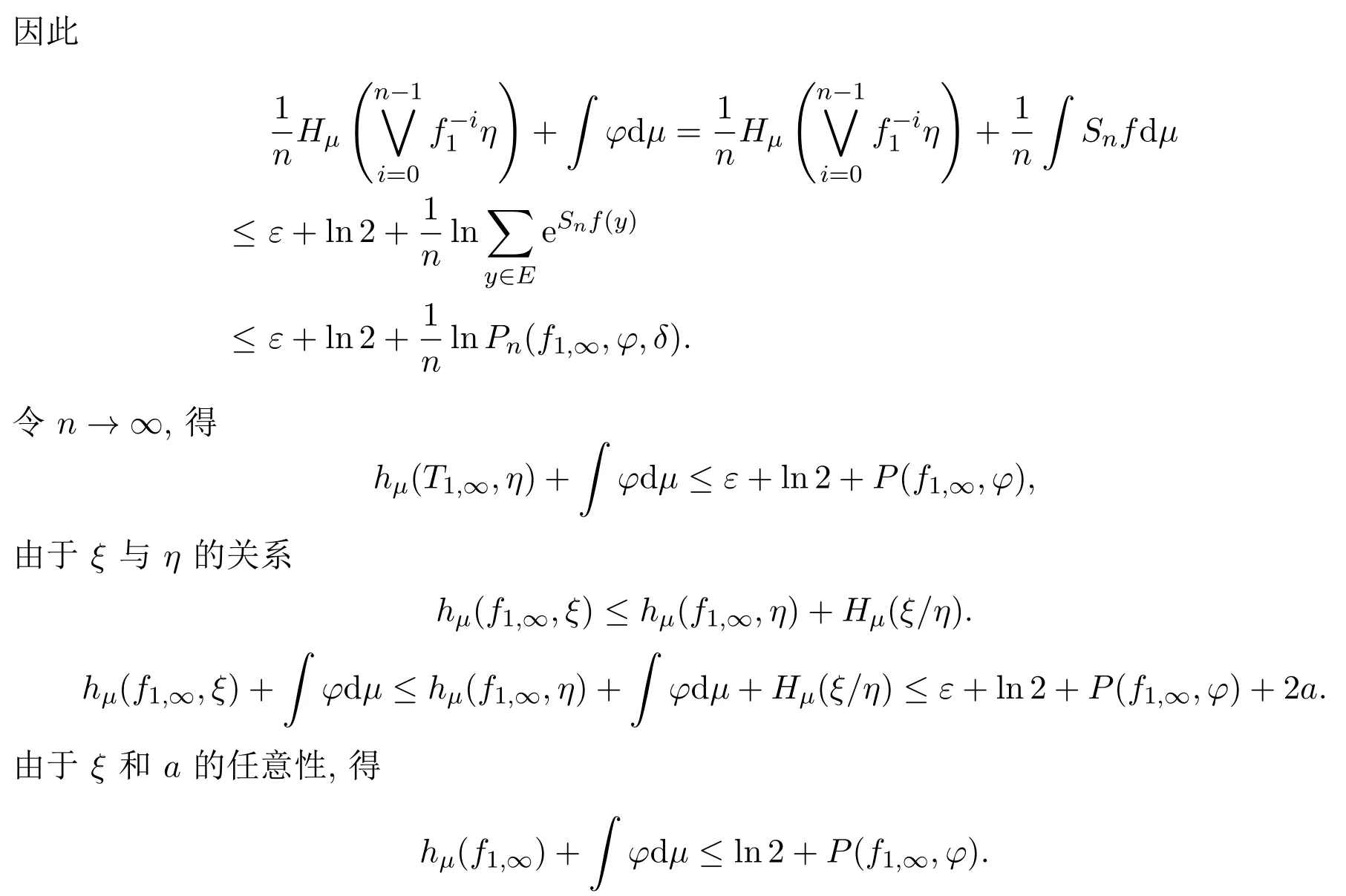
4　问题

在自治熵的变分原理中，Power Rule公式 (即 h(fk)=kh(f))极大的化简了熵的变分原理的证明过程，使得熵的变分原理的证明被更多的人接受.因此，在非自治的情况下，找到Power Rule公式成为解决非自治变分原理的重要环节.类似于熵的变分原理，压的变分原理也有P(fk，Skφ)=kP(f，φ)，在压的变分原理证明中的作用类似于自治变分原理的Power Rule公式，遗憾的是在非自治的情况下是不成立的，文献[7]中给出了反例，正因为这样，无论是非自治熵的变分原理还是非自治压的变分原理，都没有给出变分原理成立的充分必要条件.在此提出两个问题：

(2)是否可以改进定理3.1的证明给出非自治拓扑压变分原理成立的充分必要条件.

[1]Zhu Y J，Liu Z F，Zhang W D.Entropy of nonautonomous dynamical systems[J].J.Korean Math.Soc.，2012，49：165-185.

[2]Jose S，Ćanovas.On entropy of non-autonomous discrete systems partic[J].Japnts of International Conference Dynamical Systems，2013：143-159.

[3]Christoph Kawan.Metric entropy of nonautonomous dynamical systems[J].arXiv：1304.5682v2[math.DS] 16 Jul.2013.

[4]Walters P.An Introduction to Ergodic Theory[M].New York：Springer Verlag，1982.

[5]孙文祥.遍历论[M].北京：北京大学出版社，2012.

[6]Kolyada S，Snoha L.Topological entropy of nonautonomous dynamical systems[J].Random Comput.Dyn.，1996，4：205-233.

[7]Huang X J，Wen X，Zeng F P.Topological pressure of nonautonomous dynamical systems[J].Nonlinear Dynamics and Systems Theory，2008，8(1)：43-48.

Remarks on variational principle of topological pressure of nonautonomous dynamical systems

Yang Jiang，Guo Yaxiao
(College of Mathematics，Northwest University，Xi′an710127，China)

This article uses the method similar to variational principle of nonautonomous entropy，proves variational principle of nonautonomous topological pressure about an inequality，introduces the principle of variational principle of nonautonomous entropy，and enriches the content of variational principle.

entropy of onautonomous，topological pressure of nonautonomous，variational principle

O189

A

1008-5513(2015)01-0036-07

10.3969/j.issn.1008-5513.2015.01.005

2014-10-10.

国家自然科学基金(11301417，11371292).

杨将(1987-)，硕士生，研究方向：拓扑动力系统与遍历论.

2010 MSC:22A30