一类耦合Benjamin-Bona-Mahony型方程组的新精确解

赵烨，徐茜

(1.北京石油化工学院数理系，北京 102617；2.北京联合大学基础部，北京 100101)

一类耦合Benjamin-Bona-Mahony型方程组的新精确解

赵烨1，徐茜2

(1.北京石油化工学院数理系，北京 102617；2.北京联合大学基础部，北京 100101)

主要研究一类耦合的Benjamin-Bona-Mahony型方程组的显式行波解.应用展开法，Jacobi椭圆函数展开法以及详细的计算，得到了方程组的多个精确行波解.所得结果推广了方程组的sech ξ型孤立波解的存在性结果.

行波解；Benjamin-Bona-Mahony型方程组；展开法；Jacobi椭圆函数展开法

1　引言

众所周知，数学物理以及工程中的许多现象可以用非线性发展方程来描述.这些方程的解的存在性以及解的形式有助于更好的解释数学物理以及工程中的现象.所以寻找非线性发展方程的精确解是一个重要而又有趣的热点问题.对此已经提出了许多重要的方法，并得到了丰富的研究结果[1-8].

本文主要研究如下非线性发展方程组的显式行波解：

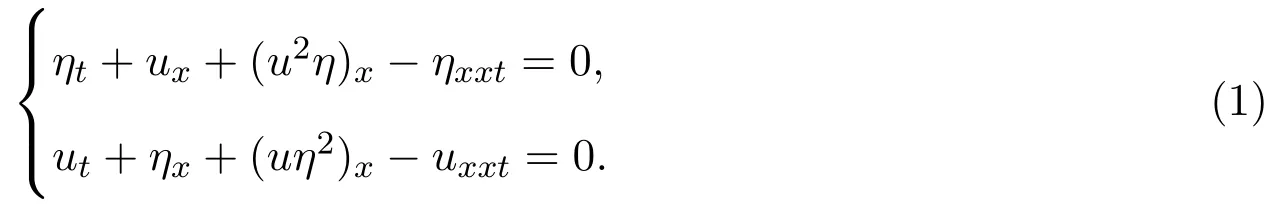
这个方程为文献 [9]中 p=1的情形，它描述了水面上的小振幅长波.文献 [9]得到了 (1) 的sech ξ型的孤立波解，其中ξ=x−ct，c代表波速.

2　双曲函数、三角函数和有理函数解

对(1)式引入行波变换η(x，t)=φc(ξ)，u(x，t)=ψc(ξ)，得到

将(2)式积分一次，积分常数分别记为C1，C2，得到

λ和µ是实常数.利用(5)式的通解形式，得

求解以上代数方程组，得到未知变量的两组值：

其中，c和λ为任意常数.

将(9)式和(10)式分别代入(4)式，得到方程组(3)两组解的表达式：

进一步，利用方程(5)的通解表达式(6)，得到方程组(1)的三种函数形式解.

a.当λ2−4µ＞0，即−1＜c＜0时，(1)式有双曲函数形式解：

b.当λ2−4µ＜0，即c＜0或c＜−1时，(1)式有三角函数形式解：

c.当λ2−4µ=0，即c=−1时，(1)式有有理函数形式解：

注 2.1如果c1̸=0，c2=0，(11)式即为：

3　Jacobi椭圆函数解

本节求解方程组(2)的Jacobi椭圆函数形式解.考虑在(2)式中最高阶导数项和非线性项的齐次平衡，设方程组(2)具有如下形式的解，其中cn为cnoidal函数，dn为dnoidal函数，

其中a1，a0，b1，b0，k为待定常数.

将(16)式代入(2)式，得到关于待定常数的代数方程组：

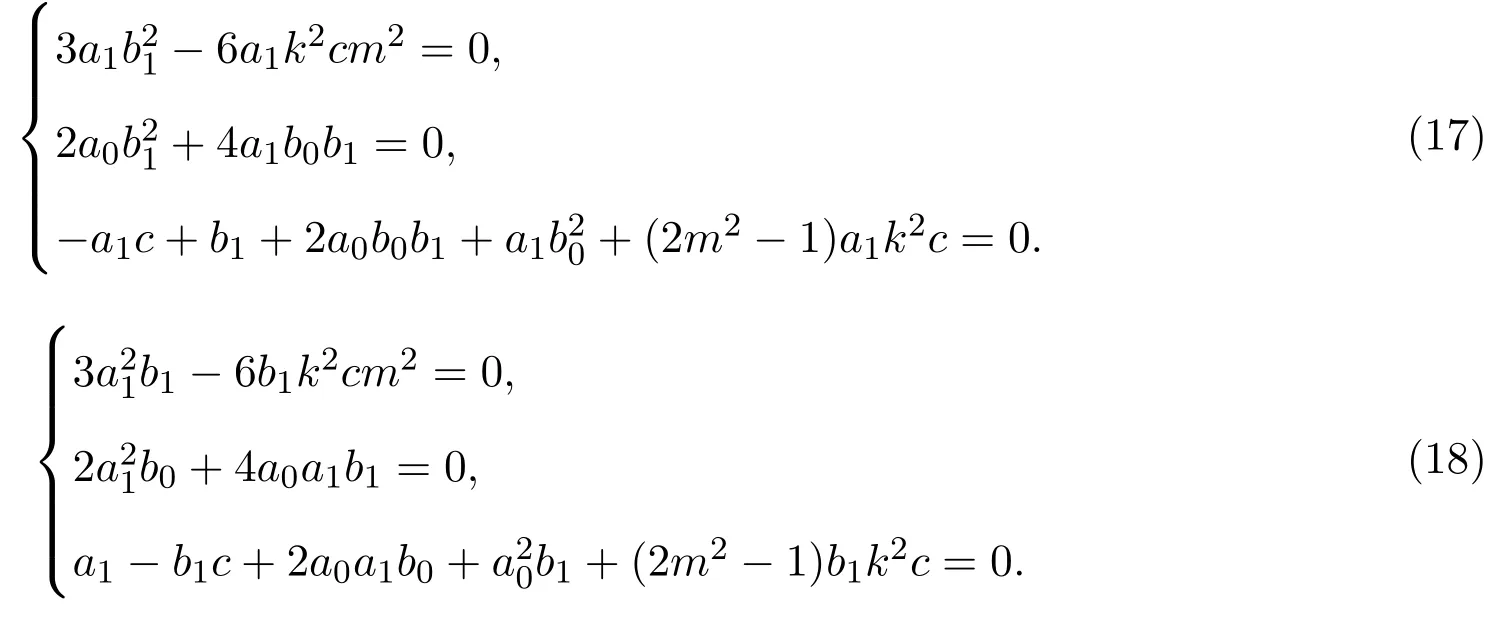
其中m(0＜m＜1)是模数.求解(17)式和(18)式，得到未知量的两组值：

将(19)式和(20)式分别代入(16)式，得到方程组(1)的cnoidal函数形式解：

再次设方程组(2)具有如下形式的解：

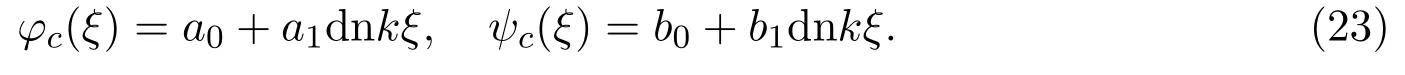
将(23)式代入(2)式，得到关于待定常数的代数方程组：

求解(24)式和(25)式，得到未知量的两组值：

将(26)式和(27)式分别代入(23)式，得到方程组(1)的dnoidal函数形式解：

注3.1如果m=1，(21)(28)式和(22)(29)式即为文献[9]中的孤立波解：

[1]Wang M，Li X，Zhang J.The-expansion method and traveling wave solutions of nonlinear evolution equations in mathematical physics[J].Physics Letters A，2008，372：417-423.

[2]Ali Akbar M，Norhashidah Hj Mohd Ali，Zayed E M E.A generalized and improved-expansion method for nonlinear evolution equations[J].Mathematical Problems in Engineering，2012，Article ID 459879，22 pages.

[3]Taha W M，Noorani M S M，Hashim I.New exact solutions of sixth-order thin-film equation[J].Journal of King Saud University-Science，2014，26：75-78.

[4]Liu Shikuo，Fu Zuntao，Liu Shida，et al.Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations[J].Physics Letters A，2001，289：69-74.

[5]Fu Zuntao，Liu Shikuo，Liu Shida，et al.New Jacobi elliptic function expansion and new periodic solutions of nonlinear wave equations[J].Physics Letters A，2001，290：72-76.

[6]Huang Wenhua，Liu Yulu，Lu Zhiming，et al.The extended Jacobi elliptic function expansion method and its applications in weakly nonlinear wave equations[J].Journal of Hydrodynamics Ser.B，2006，18(3)：352-361.

[7]王倩，陈晓燕.扩展的Sinh-Gordon方程展开法与Kaup-Kupershmidt方程的Jacobi椭圆函数解[J].纯粹数学与应用数学，2013，29(2)：159-163.

[8]曹瑞.带色散项的高阶非线性Schrödinger方程的精确解[J].纯粹数学与应用数学，2012，28(1)：92-98.

[9]Cui Liwei.Existence，orbital stability and instability of solitary waves for coupled BBM equaions[J].Acta Mathematicae Applicatae Sinica，English Series，2009，25：1-10.

New explicit solutions for some coupled Benjamin-Bona-Mahony type equations

Zhao Ye1，Xu Qian2
(1.Department of Mathematics and Physics，Beijing Institute of Petrochemical Technology，Beijing102617，China；
2.Department of Basic Courses，Beijing union university，Beijing100101，China)

This paper mainly investigates explicit traveling wave solutions for some coupled Benjamin-Bona-Mahony type equations.Applying the-expansion method and Jacobi elliptic function method，and by detailed computation，many traveling wave solutions are obtained.The results extend the existence result of sech ξ type solitary wave solutions for the equations.

traveling waves，Benjamin-Bona-Mahony equaiton，-expansion method， Jacobi elliptic function expansion method

O175.2

A

1008-5513(2015)01-0012-06

10.3969/j.issn.1008-5513.2015.01.002

2014-03-05.

北京市教委科技计划项目(KM201210017008，KZ201310028030)；北京石油化工学院青年基金(N1004).

赵烨(1978-)，博士，讲师，研究方向：偏微分方程.

2010 MSC:35Q58