分数阶微分方程m点边值共振问题解的存在性

桂旺生，刘利斌

(池州学院数学与计算机科学系，安徽 池州　247000)

分数阶微分方程m点边值共振问题解的存在性

桂旺生，刘利斌

(池州学院数学与计算机科学系，安徽 池州247000)

利用Mawhin延拓定理考察了一类分数阶微分方程m点边值共振问题解的存在性.得到了解的存在性的一个充分性条件，并且举出实例用以说明主要结果.

分数阶微分方程；Mawhin延拓定理；共振

1　引言

本文主要研究如下一类分数阶微分方程m点边值共振问题解的存在性：

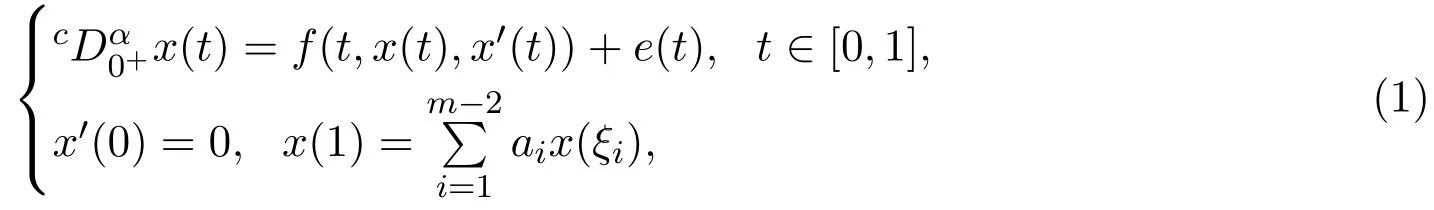
分数阶微分方程是微分方程理论的一个新的重要分支，它在扩散和输送理论、混沌与湍流、高分子材料解链、粘弹性力学及非牛顿力学等领域都有广泛的应用.对于分数阶微分方程二点与多点边值问题，许多学者对其作了一系列的研究，得到了解和正解存在性的一些结果[1-6].例如，文献[1]中利用重合度理论研究了如下分数阶微分方程二点边值问题解的存在性：

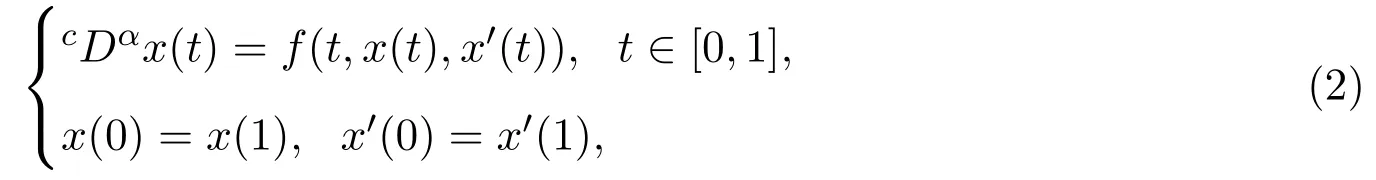
文献[5]中构造了一个特殊的锥，利用非紧性测度理论和锥拉伸与锥压缩不动点定理证明了如下m点边值问题的正解的存在性，得到了有关正解存在性的三个定理.

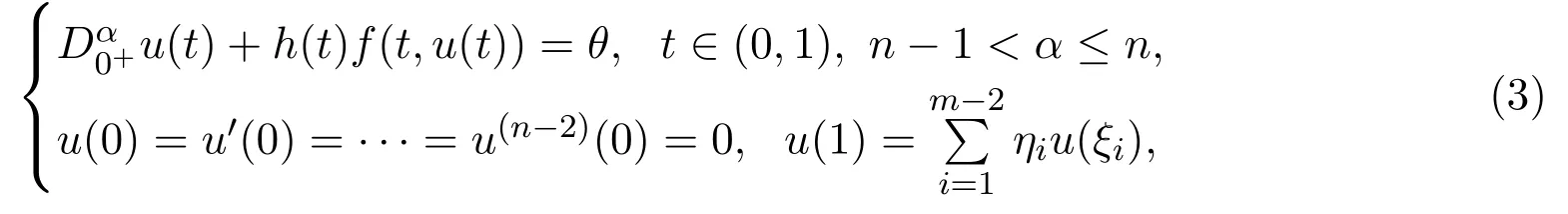
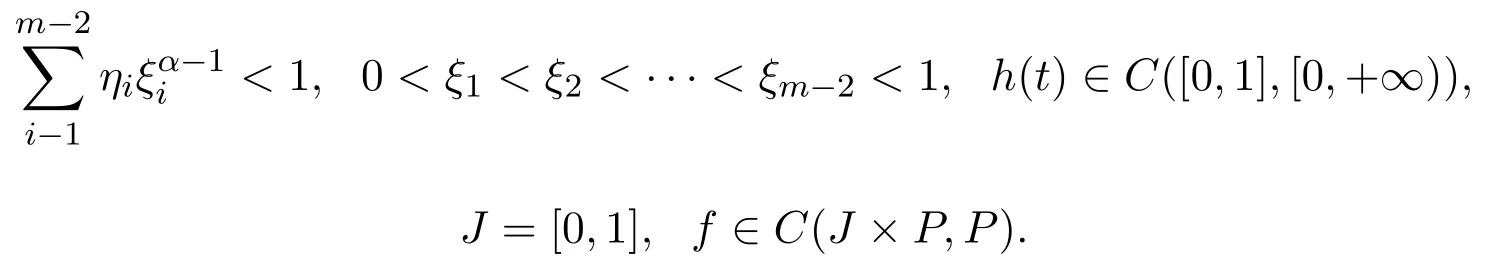
本文受以上文献的启发，主要应用重合度理论研究分数阶微分方程m点边值问题(1)的解的存在性.首先给出了与分数阶微分方程有关的几个定义与引理，其次得到了本文的主要结果，即解的存在性定理，最后举出实例作为应用.

2　几个引理

首先给出下面几个相关定义和引理：

定义 2.1[7-8](Riemann-Liouville)设函数u(t)可积，α阶积分定义为：

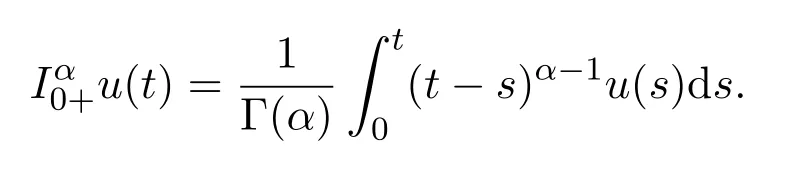
定义 2.2[7-8](Riemann-Caputo)设函数u(t)可积，α阶导数定义为：

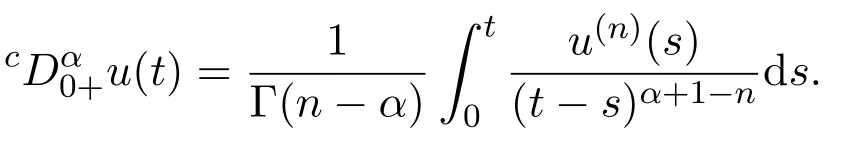
引理 2.1[8]设n−1＜α＜n，则分数阶微分方程有解：

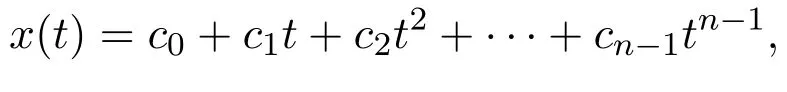
其中ci∈R，i=1，2，···，n−1.

引理 2.2[8]设n−1＜α＜n，则

其中ci∈R，i=1，2，···，n−1.

设X和Y为实Bananch空间，L：X⊃dom L→Y是线性算子，如果L满足：

(i)Im L是闭子空间；

(ii)dim Ker L=co dim Im L＜+∞；

则称L是零指标的Fredholm算子.

记X=Ker L⊕X1，Y=Y0⊕Im L.设

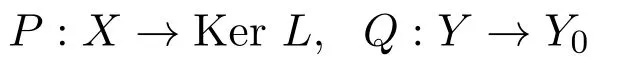
为连续投影算子.记Lp：dom L∩X1→Im L是L在dom L∩X1上的限制.

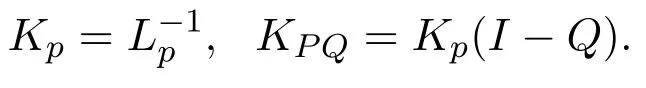
设Ω为X的有界开子集，且dom L∩Ω̸=ϕ，L：dom L⊂X→Y是零指标的Fredholm算子，N：Ω→Y为连续算子，如果QN：和KPQ：都是紧算子，则称N在上是L-紧的.

引理 2.3[9](Mawhin延拓定理)设 L：dom L⊂X → Y是零指标的 Fredholm算子，N：X→Y在上是L-紧的.若满足：

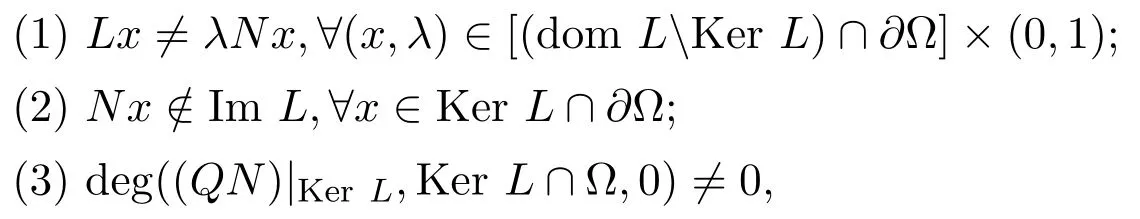
本文中，设X=C1[0，1].其上的范数定义为：

3　主要结果

引理3.1设L由(4)式所定义，则

引理3.2设L由(4)式所定义，则L是零指标的Fredholm算子；线性连续的投影算子P：X→X和Q：Y→Y定义如下：

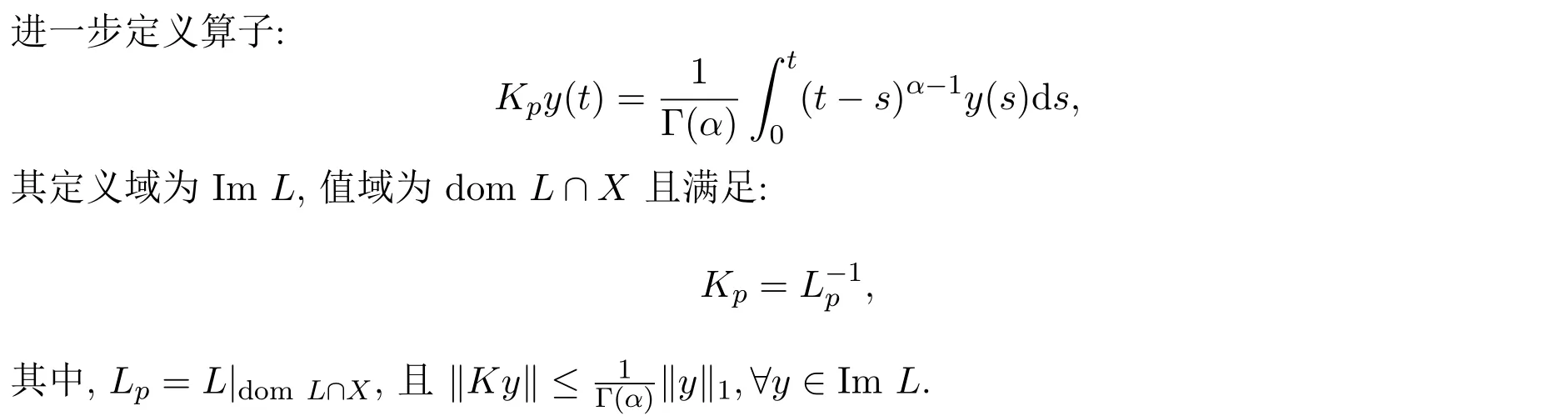
定理3.1设f：[0，1]×R2→R为连续函数.假设

4　例子

例4.1考虑下面边值问题解的存在性：

[1]Hu Zhigang，Liu Wenbin，Rui Wenjun.Periodic boundary value problem for fractional differential equation[J].International Journal of Mathematics，2012，23(10)：11.

[2]Chen Fu lai.Coincidence degree and fractional boundary value problems with impulses[J].Computers and Mathematics with Applications，2012，64：3444-3455.

[3]Li Xiaoyan，Liu Song，Wei Jiang.Positive solutions for boundary value problem of nonlinear fractional functional differential equations[J].Applied Mathematics and Computation，2011(217)：9278-9285.

[4]Zhou Wenxue，Chu Yandong.Existence of solutions for fractional differential equations with multi-point boundary conditions[J].Commun.Nonlinear Sci.Numer.Simulat.，2012(17)：1142-1148.

[5]王永庆，刘立山.Banach空间中分数阶微分方程m点边值问题的正解[J].数学物理学报：A辑，2012，32(1)：246-256.

[6]Liu Xiping，Jia Mei.Multiple positive solutions of nonlocal boundary value problems for p-Laplacian equations with fractional derivative[J].Journal of Mathematical Research with Applications，2012，32(3)：327-336.

[7]Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations[M]. Amsterdam：Elsevier Science，2006.

[8]Bai Zhanbing，Lü Haishen.Positive solutions for boundary value problem of nonlinear fractional differential equation[J].Math.Anal.Appl.，2005，311：495-505.

[9]Mawhin J.Topological degree and boundary value problems for nonlinear differential equations in topological methods for ordinary differential equations[J].Lecture Notes in Mathematics，1993(1537)：74-142.

Existence of solution to m-point boundary value problem for fractional differential equations at resonance

Gui Wangsheng，Liu Libin
(Department of Mathematics and Computer Science，Chizhou College，Chizhou247000，China)

In this paper，we consider the existence of solution for m-point boundary value problem of a class of fractional differential equations at resonance by applying the coutinuation theorem of coincidence degree developed by Mawhin，and we obtain a sufficient condition for the existence of solution.Examples are given to illustrate the main results of this paper.

fractional differential equation，Mawhin′s continuation theorem，resonance

O175.8

A

1008-5513(2015)01-0001-11

10.3969/j.issn.1008-5513.2015.01.001

2014-08-04.

国家自然科学基金(11301044)；池州学院自然科研项目(2013ZRZ004).

桂旺生(1966-)，硕士，副教授，研究方向：非线性分析.

2000 MSC:34B15，26A23