关于水平井产量公式的讨论与分析

2015-10-14单保超付玉西南石油大学油气藏地质及开发工程国家重点实验室成都610500

新疆石油地质 2015年5期

单保超，付玉（西南石油大学油气藏地质及开发工程国家重点实验室，成都610500）

关于水平井产量公式的讨论与分析

单保超，付玉
（西南石油大学油气藏地质及开发工程国家重点实验室，成都610500）

介绍了水平井稳态产量公式的推导思路与推导过程，根据水平井的渗流场特征，对常用的水平井产量公式（Borisov公式、Giger公式、Joshi公式、Renard-Dupuy公式）进行了对比分析。通过分析发现，水平井产量公式在推导过程中存在疏漏，应予以修正。通过实例计算，证明了修正后的水平井产量公式与Borisov公式、Giger公式、Renard-Dupuy公式等在计算结果上有很好的一致性，实现了水平井产量公式在形式上的统一。

水平井；产量公式；对比；优化；统一

水平井是油气田增产的一种有效措施，在裂缝性油气藏、低渗油气藏等非常规油气藏的开发中有着广泛的应用。目前，关于水平井的稳态产量计算公式主要采用解析法和模拟法。这些公式虽然在推导过程和推导思路上有所不同，但最终结果却大同小异。

1　水平井产量公式推导思路

常用水平井产量公式在推导过程中，沿用Joshi[1]和Giger[2]的思路，利用面积等值的拟圆形驱动边界和生产坑道[3]的概念，借助达西定律、欧姆定律以及水电相似原理[4]，推导出陈氏水平井产量公式[5]。

1.1渗流阻力的划分及数学表达式

假设油层厚度为h，泄油面积为A，在稳产条件下，流体在驱动能量的作用下从驱动边界流向井筒，渗流场可以看成水平方向上的外部渗流阻力区和垂向上的内部渗流阻力区，其渗流阻力则分别为水平方向上的外部渗流阻力R1和垂向上的内部渗流阻力R2.

将驱动边界看成拟圆形驱动边界时，驱动半径reh与泄油面积A的关系可表示为

借助文献［6］的研究成果以及产量等值原则[3]，可将水平井的水平段等价为拟圆形生产坑道，坑道中心半径rpc=L/c（L为水平井段长度，c为转换因子，一般取4）。生产坑道自身的圆形半径为h/2，但一般来说，h/2远小于坑道中心半径L/4，故忽略坑道自身的圆形半径，将坑道的中心半径近似看作生产坑道的外边缘半径。由此可得生产坑道半径为

根据等值渗流阻力法可得从驱动外边界reh到生产坑道rpc的外部渗流阻力R1为

内部渗流阻力R2可以看作是从生产坑道半径rpc流向生产井底rw的流动。将该流动看作是高为h间上垂直并围绕水平井段的平面径向流。因此，地层L，径向流半径可看作是地层有效厚度之半即

内部渗流阻力R2可以表示为

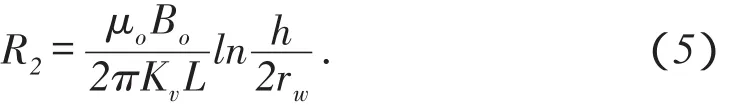
将地层视为各向同性，即Kv=Kh=K，渗流总阻力Rt是外部渗流阻力R1和内部渗流阻力R2之和，即

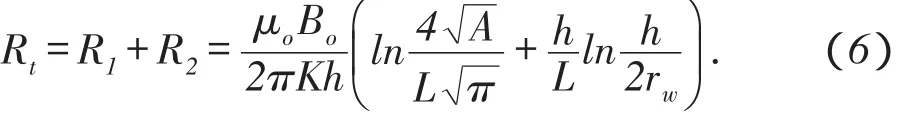
1.2产量公式的建立

在稳定流动的条件下，根据产量、压差与渗流阻力之间的关系式[4]

可以建立水平井产量公式

引入参数a，b，且满足下列关系式：

联立（8）式、（9）式、（10）式可得

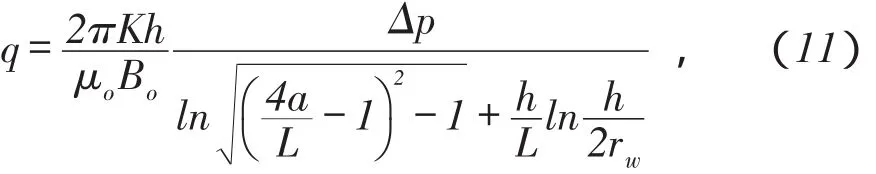
（11）式即为陈氏水平井稳态产量公式。

2　公式讨论与分析

2.1公式讨论

文献［5］在推导陈氏水平井产量公式过程中采用面积等值原则，将椭圆形驱动边界简化为拟圆形驱动边界，使得整个推导更加通俗易懂。另外，对比（8）式可见，（11）式在形式上更加简洁，便于运用。

不过，文献［5］在推导陈氏公式的过程中也存在以下3个疑点。

（1）在推导外部渗流阻力项的过程中，文献［5］采用面积等值的方法和生产坑道的概念，将椭圆形驱动边界简化为拟圆形驱动边界，得到外部渗流阻力

即内部渗流阻力中应有一个“π”。关于内部渗流阻力R2中是否有“π”，不同学者有不同的看法。文献［8］曾应用保角变换方法重新推导Joshi公式，认为Joshi公式中少了一个“π”。而Joshi则坚持没有“π”是正确的。文献［5］曾经在文章中指出这一项中不应有“π”，认为Borisov首先以俄文发表论文，经他人翻译为英文的过程中可能有问题，并质疑Giger[9]采用势流动函数和镜像反映法所得结果的正确性。事实上，陈氏公式在推导内部渗流阻力时，将水平井看作直井并将有效厚度看作水平井长度L的过程中，已有镜像反映法的应用之意。

文献［5］认为，在水平井周围，流体发生垂直于水平井段的平面径向流，它的外部半径rb为h/2，内部半径为rw，渗流场如图1所示。

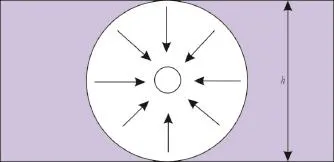
图1　陈氏公式水平井段垂向径向流示意

但是，对于上下封闭地层而言，由于封闭地层处没有流体补给，因此是无法在上下边界层h/2处发生径向流的。也就是说，如果要将此处流动等效成径向流，那么发生径向流的半径必小于地层厚度之半h/2.由此看来，径向流半径rc的大小应为h/2π，实际围绕水平井段径向流渗流场如图2所示。

图2　水平井周围垂向径向流示意

2.2常用产量公式

通过以上分析，下文重点比较陈氏公式以及在陈氏公式的内部渗流阻力项R2中加“π”后它们各自与Borisov公式[6]、Giger公式[2]、Joshi公式[1]、Renard-Du⁃puy公式[10]之间的差别。

为表述和计算方便，对各公式均采用矿场单位制。

（1）Borisov公式1964年，苏联学者Borisov系统研究了水平井的渗流原理，将水平井周围三维渗流场近似分为内部渗流场和外部渗流场。他假设水平井位于顶底封闭的各向同性油层中部，流体在地层中的流动为稳态渗流，且流体不可压缩，忽略井筒中产生的压降，利用拟三维方法得出了水平井产量公式，奠定了二维稳态分析水平井产能的基础，即

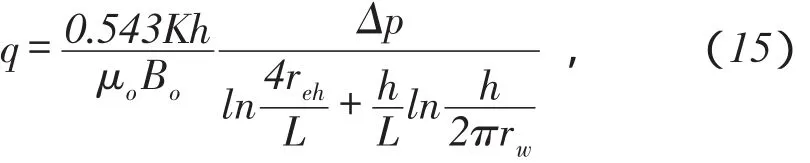
（2）Giger公式1984年，Giger利用等效半径reh替代水平面椭圆泄流区半长轴，推导出均质各向同性油藏的水平井稳态产量公式，即

（3）Joshi公式1988年，Joshi按照Borisov的思路，将水平井三维渗流场分解为内部的垂向平面径向流和外部的水平方向的椭圆流动，综合应用拟三维求解思想和势能理论，推导出了均质油藏中水平井稳态产量公式，即

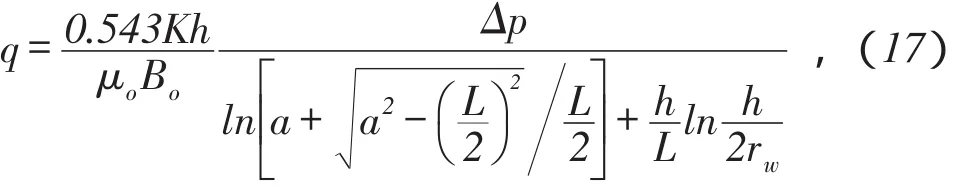
（4）第二项中加“π”之后的Joshi公式

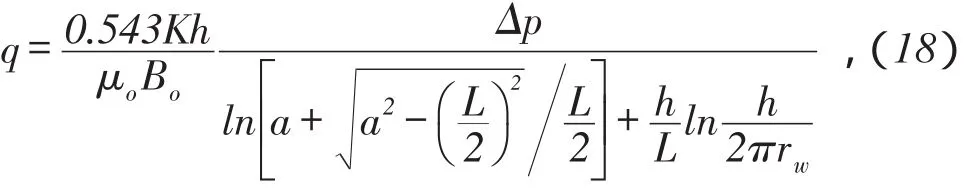
（5）Renard-Dupuy公式1991年，Renard和Du⁃puy引入表皮因子修正了Joshi的稳态产量公式，分析了井眼附近地层伤害对产能的影响。其公式为

由于恒满足2a/L>1，因此（19）式等价于

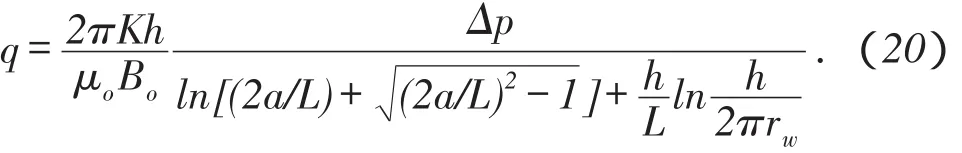
（6）陈氏公式

（7）本文修正后的陈氏公式

3　实例计算与分析

3.1实例计算

采用文献［5］中所引用的计算实例进行计算，相关参数为：泄油面积A为485 830m2，水平井段长度L为609.76m，有效厚度h为18.29m，水平和垂直渗透率K均为100mD，原油体积系数Bo为1.20，原油黏度μo为0.90mPa·s，原始地层压力pe为20.684MPa，生产压差Δp为3.447MPa，井筒半径rw为0.091 5m.通过实例计算，分析7个公式计算结果上的差异，从而间接证明，经本文修正的陈氏公式的正确性。

将已知各参数代入到相应的公式当中，计算结果如表1所示.

表1　不同公式计算的渗流阻力和产量结果对比

3.2对比分析

对表1的计算结果进行分析可以得出以下结论。

（1）内部渗流阻力约为外部渗流阻力的11.71%.内部渗流阻力项如果没有“π”，可以使内部渗流阻力的值增加33.09%，但是总渗流阻力仅仅增加了3.54%，因此，内部渗流阻力项中有无“π”对产量的影响不大，约为3%.

（2）从图3可以看出，Giger公式的外部渗流阻力和渗流总阻力较其他公式明显偏高，陈氏公式[5]和Joshi公式[1]的总渗流阻力略有偏高，而本文修正的陈氏公式与Borisov公式[6]、Renard-Dupuy公式[10]以及修正Joshi公式呈现出很好的一致性。这也从侧面佐证了本文修正的陈氏公式的正确性。

图3　不同公式计算的渗流阻力对比

（3）由图4可知，根据不同的公式计算出的产量各不相同。与总渗流阻力相对应，产量大小分布也大致呈现出3个阵营，即：Giger公式产量明显偏低，陈氏公式[5]和Joshi公式[1]产量略有偏低，而Borisov公式[6]、修正的Joshi公式、Renard-Dupuy公式[10]以及本文修正的陈氏公式4者之间有很好的一致性。由于Giger公式[2]没有详细的推导过程，其产量偏低的具体原因也就无从得知。陈氏公式和Joshi公式产量偏低的原因主要是因为内部渗流阻力项中少了一个“π”，是内部渗流阻力项偏大的必然结果。值得指出的是，本文修正的陈氏公式与Borisov公式虽然在形式上不同，但是各参数的选取和计算是完全相同的，计算得到的产量自然也完全相同。

图4　不同公式计算的产量对比

4　结束语

（1）通过分析可见，内部渗流阻力项中应统一有“π”，这既是在形式上的统一，又是分析和计算之后的必然结果。文献［5］中曾提到在水平井的周围发生的是垂直于水平井段的平面径向流，渗流外部半径为h/2，内部半径为rw.既然是上下封闭的地层，那么在上下距井h/2处是不可能有流体供给的，其泄流半径也不可能是h/2，而应该是hπ/2.

（2）文献［5］所推导的水平井产量公式的外部渗流阻力项虽然在形式上有别于Borisov公式，但二者在实质上却是相同的。陈氏公式在推导过程中用拟圆形的驱动边界代替了椭圆形驱动边界，但又在求解的过程中引入了参数a，b，并且给出了a，b的表达式，这是没有必要的。当然，文献［5］中水平井产量公式的推导过程从侧面证明了Borisov公式的正确性，该公式思路明确，通俗易懂，不失为一种很好的计算水平井产量的公式。

（3）目前，关于水平井的稳态产量公式研究较多，也较为成熟。国内外学者对水平井的稳态产量公式作了大量研究[11-18]，并各自在自身理论成果研究的基础上推导出了相应的水平井产量公式。这些公式虽然在形式上有所不同，但是计算结果却相差不大。计算结果的差异大多是由于假设条件不同而产生的。相比较而言，关于水平井拟稳定产能、不稳定产能以及考虑地层与流体流动相耦合的水平井不稳定产能等方面研究较少，而这些却更为贴近现场实际，特别是对于低渗油气田的开发有着更为显著的作用。因此，在以后的研究当中，将重点放在更加贴近现场实际、去掉多余的假设条件等方面会更有意义。

符号注释

a——椭圆形长轴半长，m；

A——泄油面积，m2；

b——椭圆形短轴半长，m；

Bo——原油体积系数，m3/m3；

c——转换因子，无因次；

h——储集层厚度，m；

Kh——水平方向渗透率，mD；

Kv——垂直方向渗透率，mD；

L——水平井段长度，m；

pe——原始地层压力，MPa；

Δp——生产压差，MPa；

q——产量，m3/d；

rb——径向流半径，m；

rpc——生产坑道半径，m；

reh——驱动半径，m；

rw——井筒半径，m；

R1——水平方向上的外部渗流阻力，MPa·d/m3；R2——垂直方向上的内部渗流阻力，MPa·d/m3；Rt——总渗流阻力，MPa·d/m3；

μo——原油黏度，mPa·s.

［1］Joshi SD.Augmentation ofwell production using slantand horizon⁃talwells［R］.SPE 15375，1986.

［2］Giger FM.Horizontalwells production techniques in heterogenous reservoir［R］.SPE 13710，1985.

［3］陈元千.油气藏工程计算方法［M］.北京：石油工业出版社，1990：138-151.

Chen Yuanqian.Reservoirengineering calculationmethods［M］.Bei⁃jing：Petroleum Industry Press，1990：138-151.

［4］李晓平.地下油气渗流力学［M.北京：石油工业出版社，2005：85-87.

Li Xiaoping.Underground oil gas seepagemechanics［M］.Beijing：Petroleum Industry Press，2005：85-87.

［5］陈元千.水平井产量公式的推导与对比［J］.新疆石油地质，2008，29（1）：68-71.

Chen Yuanqian.Derivation and correlation ofproduction rate formula for horizontal well［J］.Xinjiang Petroleum Geology，2008，29（1）：68-71.

［6］Borisov JP.Oil production using horizontal and multiple deviation wells［M］.Moscow：Nedra，1964.

［7］窦宏恩.预测水平井产能的一种新方法［J］.石油钻采工艺，1996，18（1）：76-81.

Dou Hongen.A new method forpredicting productivity ofhorizontal wells［J］.OilDrilling Technology，1996，18（1）：76-81.

［8］李汤

玉.水平井产量公式分析［J］.石油勘探与开发，1997，24（5）：76-79.

LiDang.Analysisofproductivity formulaforhorizontalwells［J］.Pe⁃troleum Exploration and Development，1997，24（5）：76-79.

［9］Ahmed T.Reservoirengineeringhandbook［M］.Houston，Texas：Gulf Publishing Company，2000：515-531.

［10］Renard G，Dupuy JM.Formation damage effects on horizontalwell flow efficiency［J］.Journal ofPetroleum Technology，1991，43（7）：786-789.

［11］郭肖，陈路原，杜志敏.关于Joshi水平井产能公式的探讨［J］.

西南石油学院学报，2003，25（2）：41-43.

Guo Xiao，Chen Luyuan，Du Zhimin.Discussion on the productivity formula ofJoshiforhorizontalwells［J］.Journal ofSouthwestPetro⁃leum Institute，2003，25（2）：41-43.

［12］Elgaghad SA，Osisanya SO，Tiab D.A simple productivity equa⁃tion for horizontal wells based on drainage area concept［R］.SPE 35713，1996.

［13］FuruiK，Zhu D，Hill AD.A rigorous formation damage skin factor and reservoir inflow model for horizontal wells［R］.SPE 84964，2003.

［14］郎兆新，张丽华，程林松，等.多井底水平井渗流问题某些解析解［J］.石油大学学报：自然科学版，1993，17（4）：40-47.

Lang Zhaoxin，Zhang Lihua，Cheng Linsong，et al.Some analytical solutions for seepage problems in horizontalwellswithmultiwell bottoms.［J］.JournalofPetroleum University：Natural Science Edi⁃tion，1993，17（4）：40-47.

［15］李真祥，王瑞和，刘继林，等.封闭边界油藏水平井产能模型［J］.钻采工艺，2008，31（6）：66-68.

Li Zhenxiang，Wang Ruihe，Liu Jilin，etal.The productivitymodel ofhorizontalwells in closed boundary reservoirs［J］.Drilling Tech⁃nology，2008，31（6）：66-68.

［16］吕劲.水平井稳态产油量解析公式及讨论［J］.石油勘探与开发，1993，20（增刊）：135-140.

Lyu Jin.Stable oil production rate analytical formula forhorizontal wells and discussion［J］.Petroleum Exploration and Development，1993，20（suppl.）：135-140.

［17］陈小凡，乐平，苏国丰，等.一种新的水平井产量计算公式［J］.西南石油大学学报：自然科学版，2010，32（1）：93-96.

Chen Xiaofan，Le Ping，Su Guofeng，et al.A new productivity for⁃mula for horizontalwells［J］.Journal of Southwest Petroleum Uni⁃versity：NaturalScience Edition，2010，32（1）：93-96.

［18］袁迎中，张烈辉，王健.水平井稳态产能公式及其改进［J］.新疆石油地质，2009，30（1）：77-80.

Yuan Yingzhong，Zhang Liehui，Wang Jian.Stable productivity for⁃mula forhorizontalwellwith improvement［J］.Xinjiang Petroleum Geology，2009，30（1）：77-80.

Discussion and Analysisabout HorizontalW ell Productivity Formulas

SHANBaochao,FUYu
(State Key Laboratory ofOiland Gas ReservoirGeology and Exploitation，SouthwestPetroleum University，Chengdu,Sichuan 610500，China)

This paper introduces the deducing ideasand processes ofsteady⁃state productivity formulas forhorizontalwells,and compares the commonly used formulas.Through the analysis,it is indicated that there are loopholes in the processofdeducing the productivity formu⁃lasforhorizontalwells,which should be corrected.There are little differencesamong themodified formula,Borisov’sformula,and Renard⁃Dupuy’sformula in the calculation results,thus providng the validity and practicability ofthemodified formula,and realizing the unifica⁃tion ofproductivity formulasforhorizontalwells in form.

horizontalwell;productivity formula;comparison;optimization;unification