页岩气藏体积压裂水平井产能模拟研究进展

周祥，张士诚，马新仿，张烨（中国石油大学石油工程学院，北京102249）

页岩气藏体积压裂水平井产能模拟研究进展

周祥，张士诚，马新仿，张烨
（中国石油大学石油工程学院，北京102249）

页岩气储层孔喉细小，渗透率极低，一般无自然产能，需借助水平井和体积压裂技术才能实现经济开发。国内外关于页岩气的研究多集中于地质评估和开发工艺，而适用于页岩气体积压裂水平井产能的理论研究相对较少。页岩气产能研究的关键在于多尺度渗流机制的准确描述和复杂裂缝网络的精细表征。通过广泛调研和分析，探讨了页岩储层多尺度渗流机制；总结了页岩气藏多裂缝水平井试井模型，阐述了不同模型关于流态划分、储层和裂缝参数评估的应用；系统介绍了页岩气数值模拟方法，包括常规数值模拟方法、离散裂缝网络模型方法及有限元方法，认为后两者是未来页岩气产能数值模拟的发展趋势。

页岩气；体积压裂；水平井；产能

页岩气为产自极低孔隙度和渗透率、以富有机质页岩为主的储集岩系中的天然气[1-2]。由于页岩气储层物性差，需要借助大型水力压裂技术制造复杂裂缝系统，才能实现工业化生产，因此，页岩气藏又被称作“人造气藏”[3]。美国是全球页岩气开发最成功的国家，30多年大规模商业化开采积累了大量的现场经验，引领了该领域的技术革新；中国自2005年开展了规模性的前期探索，并借鉴北美经验，努力寻求页岩气产业的快速发展。纵观国内外页岩气的发展历程，人们为成功开发这一潜在的巨大资源开展了大量的研究工作，主要集中在以下方面：储层的孔喉结构、岩石脆性及矿物成分、储层地化特征（有机质含量、热成熟度等）、气体存储及运移机制、压裂工艺技术、复杂裂缝扩展和压后产能预测。总体而言，有关页岩气的地质认识和开发工艺技术的研究相对成熟和系统，已形成了远景页岩气资源的地质评价标准和成功开发页岩气的工艺配套技术；而页岩气压后产能预测一直是研究难点，一是因为页岩气储层压后复杂裂缝系统难以表征，二是页岩孔喉复杂，气体赋存形式多样，多尺度下气体微观渗流机理难以描述，缺乏整合各种流动机制的气藏工程方法和模拟技术。本文通过广泛调研国内外页岩气产能分析和模拟技术，首先阐述了页岩气储层中存在的微观渗流机制；详细介绍了试井分析方法中裂缝处理方式、渗流机制及方法应用；对比了单孔单渗模型、双孔单渗模型和双孔双渗模型的特点；最后着重介绍了页岩气储层产能模拟中的裂缝表征方法，展望了未来页岩气储层产能数值模拟技术的发展方向。

1　渗流机制

页岩气独特的赋存和流动机制是页岩气藏数值模拟的难点之一。国内外许多学者借助高精度的电镜扫描技术和能量分散光谱分析技术等，能清楚地观测到页岩矿物组成和微观孔隙结构，分辨不同类型和尺度的孔隙特征，包括有机质中纳米孔、黏土矿物粒间孔、岩石骨架矿物孔、生物化石孔和微裂缝等，孔隙尺寸主要集中在纳米级。孔隙特征影响着气体的吸附能力和气体的运移机制。

1.1吸附和解吸附

有机质纳米孔是天然气的重要存储空间，文献［4］指出，20%~85%页岩气是以吸附态存储于有机质中，剩余的气体以自由气形式存在于微孔隙和天然裂缝中。页岩储集层中，随着生产的进行，储层压力下降，气体从有机质中解吸附，解吸附规律一般采用Lang⁃muir等温吸附曲线描述[5]。

1.2基于克努森数划分的气体运移机制

大量实验研究表明，页岩气储层的孔隙远小于砂岩和碳酸盐岩储集层，主要介于纳米和微米之间。如Haynesville盆地页岩气储层的孔径为20 nm[6]，Barnett页岩气储层的孔径为5~750 nm，平均为100 nm[7]。随着流动通道变窄，气体分子的运移方式发生变化，达西定律不再适用，目前较为普遍接受的方法是根据克努森数对流动形态进行划分，并分别采用相应的模型描述流动特征。克努森数（Kn）定义为分子平均自由程与平均水力半径的比值，根据克努森数的大小将流态划分为连续流、滑脱流、过渡流和克努森扩散。

（1）连续流这个流动区域的Kn小于0.001，即分子平均自由程相对于孔喉尺寸可以忽略不计，分子间的碰撞很明显，而分子与孔壁的碰撞可以忽略不计，达西公式可以很好地表征连续流。微米级孔隙的常规油藏渗流机制属于这个范畴[8]。

（2）滑脱流这个流动区域的Kn为0.001~0.1，该渗流机制下，孔隙壁面的流动速度为0，黏性流理论需作相应的修改以满足边界滑脱。由于分子平均自由程与孔喉尺寸比值增大，流动介质分子与孔隙壁面的碰撞相对于分子间的碰撞逐渐变得明显。最早，克林肯伯格滑脱理论能用于描述该渗流机制；后来很多学者通过实验方法[9-12]，对克林肯伯格滑脱因子进行修正，或者引入克努森参数校正。许多致密气藏渗流机制属于这个范畴。

（3）过渡流这个流动区域的Kn为0.1~10，这个流态的流动特征最难以模拟，但是却又举足轻重，因为大多数的页岩储层和致密气藏都在这个范畴。该流态可用克努森修正的达西公式描述，但是其准确性受到学者的质疑[13]。

（4）克努森扩散这个流动区域的Kn大于10，该渗流机制下，气体分子平均自由程远大于孔径，分子与孔壁的碰撞占主导形式，分子间的碰撞可忽略，流动特征可以用克努森扩散方程表示。具有非常细小孔喉直径的页岩储层或煤层中存在该流动机制。

纳米级孔隙中的分子运动可以用不同的方法来模拟，比如分子动力学（molecular dynamics）、蒙特卡洛直接模拟法（directsimulation Monte Carlo）、Burnett方程和格子-玻尔兹曼方法（Lattice-Boltzmann），但是这些方法计算非常耗时，难以用于油藏级别渗流机制的模拟。为了保证模拟的可行性，通常做法是把不同的渗流机制整合到标准的达西方程中，用克努森数修正后的表观渗透率代替普通渗透率，从而开展油藏数值模拟[14]。

2　试井分析方法

2.1未压裂或压裂直井试井模型

文献［15］于1980年最早提出了页岩气藏不稳定压力试井数学模型，模型采用了双重孔隙介质，详细给出了模型解析解；但是解析解模型中未考虑解吸附、扩散、滑脱等渗流机制，并假设所有参数与油藏压力无关。基于该模型，文献［15］对Devonian页岩气进行了压力恢复试井和压降试井分析，求取了裂缝和基质的孔隙度和渗透率。文献［16］通过耦合常规双孔介质模型和解吸附、扩散机制，建立了页岩气压裂直井的渗流模型，研究了页岩气藏渗流规律。但是模型中将水力裂缝等效成井径扩大的不压裂直井，因此，该模型计算的压力响应特征不能反映压裂井的渗流流态。

2.2多裂缝水平井试井模型

水平井多段压裂工艺技术的成功应用，使页岩气产量得到大幅提升，与之相应的水平井多段压裂试井模型也得到了快速发展。理论上，页岩气压裂水平井不稳定渗流存在多种流态，但是这些流态是否会出现与油藏的泄油区域形状、水平井长度、油藏非均质性和完井方式等有关，学者们根据各自对页岩气井生产特点的认识建立了不同的模型。

2010年，文献［17］采用不稳定压力试井方法，基于线性流的假设，建立了页岩气多段压裂水平井渗流模型，利用页岩气水平井早期产气数据，评估水力裂缝半缝长和页岩基质渗透率。文献［18］提出了双孔介质线性流模型，分析了页岩气多段压裂水平井不稳定线性渗流阶段的特征，该模型适用于只出现线性渗流阶段的页岩气井，通过计算可以获取泄气区域面积和裂缝间距。文献［19］提出了2种双孔介质线性流模型，模型的区别在于裂缝的处理方式不同，第一种是裂缝等间距分布，基质为平板状；第二种基质为小立方体，天然裂缝被水力压裂改造后形成具有一定导流能力的正交缝网系统。文献［19］分析了400多口页岩气井，这些井均能显示不稳定线性渗流特征，基本未出现早期线性流或者双线性流特征。通过不稳定线性流特征分析，可以计算泄气区域大小、裂缝和基质的交界面以及基质渗透率。2011年，文献［20］和文献［21］提出了三线性渗流模型，将油藏分为内油藏区域和外油藏区域，内油藏区域采用双孔介质模拟体积压裂，外油藏区域采用单孔介质；模型将水平井流态特征分为内油藏区域裂缝中流体向井筒的线性流、内油藏区域基质向裂缝中的线性流以及外油藏区域向内油藏区域的线性流3个阶段（图1）；基于三线性渗流模型，分析了外边界油藏、基质渗透率、天然裂缝渗透率和密度、水力裂缝导流能力和间距等参数对模型特征曲线的影响，并定性给出了油藏改造建议。

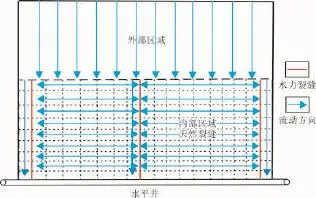
图1　三线性渗流模型示意

上述诸多关于多裂缝水平井试井模型的研究，虽已应用于页岩气井的分析，但是这些模型仍存在不足，最大的问题是没有考虑页岩气储层的解吸附、吸附、扩散和应力敏感等机制。2011年，文献［22］和文献［23］提出了页岩气藏多裂缝水平井的综合设计方法，该方法从生产角度，以一定时间段内水力压裂改造区域气体采收率大于50%为目标，基于试井模型给出了优化的裂缝间距；同时建立了净收益模型，从经济效益角度对缝间距进一步优化，最终给出综合的优化结果。模型中引入了吸附指数，能反映吸附气对压力变化的影响，解吸附规律用Langmuir模型表征。该模型中，页岩气多裂缝水平井典型流态包括裂缝储集阶段、拟线性流阶段和拟-拟稳态流阶段，后期的复合现线性流和边界流阶段在实际生产过程中一般不会出现。该模型的特别之处在于提出了拟-拟稳态流，该流态是压降分析的核心，裂缝间压力相互干扰发生于该流态，并且根据页岩渗透率和吸附指数能够计算出裂缝间干扰发生的时间，从而优化裂缝间距。文中以Fayetteville，Hayenesville及New Albany3个地区的页岩气井实际生产数据为例，详细介绍了该试井解释方法的应用。同年，文献［24］提出了压裂页岩气井历史拟合的半解析解方法。该方法与文献［18］提出的模型相同，重点分析双线性流和后期线性流阶段，不同的是采用半解析法求解，并用气体特性变化和低压下的气体解析校正；通过历史拟合，可以得到基质和裂缝渗透率、裂缝半长和原始储层含气量等。

2013年，文献［25］开发了适用于页岩气压裂水平井的数值求解器（TAMSIM），模型源于劳伦斯伯克利实验室开发的多孔介质热量和流体流动模拟模型（TOUGH+），考虑了解吸附和扩散机制，对比了不同水力裂缝、水平次裂缝和天然裂缝组合方式对压力分布和产能特征的影响。文中细化了水力压裂改造区域的描述，提出了7种组合方式（图2），包括①单一平面横切缝；②横切缝和水平次裂缝系统（全贯穿）；③横切缝和天然裂缝系统（全贯穿）；④横切缝、水平次裂缝和天然裂缝系统（全贯穿）；⑤横切缝和水平次裂缝系统（半贯穿）；⑥横切缝天然裂缝系统（半贯穿）；⑦横切缝、水平次裂缝和天然裂缝系统（半贯穿）。将流态划分为线性流、复合线性流和椭圆流，基于不同的流态和模型可以得到油藏特征参数。文献［26］提出了页岩气水平井多裂缝试井模型，考虑了解吸附、扩散和应力敏感特征，模型中裂缝可以与水平井存在一定夹角，采用拉普拉斯变换、点源函数、数值离散等方法求解。绘制了特征曲线，将流态划分为早期线性流、拟径向流、中期线性流和后期拟径向流，并分析了主要参数对特征曲线的影响。

图2　水力压裂改造区域裂缝表征模型

3　数值模拟方法

国内外学者就页岩气数值模拟开展了大量研究，在数值模型方面，包括单孔介质模型、双孔介质模型（单渗/双渗）以及三孔介质模型，其中双孔介质模型应用最为广泛。在渗流机制方面，几种模型都考虑了解吸附机制，不同的是单孔介质模型未考虑基质和裂缝中流动方式的差异，都假设为达西流；双孔单渗模型认为气体从基质中以扩散方式流向裂缝，再从裂缝以达西流方式运移至井筒，基质间不发生流动；双孔双渗模型认为基质与基质、基质与裂缝间均存在气体运移，且运移服从菲克扩散定律，裂缝中气体流动符合达西定律；三孔介质模型本质上与双孔双渗模型相似，不同在于将基质进一步划分为有机质基质和基质微裂缝。现有的文献关于模型的机制阐述较少，更多的报导是运用模型对产能进行模拟分析，而模拟产能时很重要的一点是关于水力压裂改造区域的表征。笔者按照水力裂缝处理方式将数值模拟方法分为常规方法和非常规方法。

3.1常规数值模拟方法

大量微地震监测结果表明，页岩储层压裂后在一定空间内形成复杂的裂缝网络[27-29]，由于基质渗透率极低，网络裂缝是渗流的主要通道，所以压后裂缝系统的表征是产能模拟的核心环节。基于不同的孔隙介质渗流模型，结合微地震监测结果，将复杂缝网简化成平面缝、规则正交缝网或分区表征是较为常规的裂缝表征方法。

2009年，文献［30］用数值模拟方法研究了页岩气产能。采用正交裂缝网络模拟复杂裂缝，裂缝网络如图3所示，垂直于井筒方向的裂缝为主裂缝，平行于井筒方向的裂缝为次生裂缝；分析了主裂缝和次裂缝中导流能力分布、裂缝复杂程度、基质渗透率等对产能和最终采收率的影响。2011年，文献［31］进一步从微地震监测到数值模拟进行了全面论述，提到油藏数值模拟时结合网格自动化划分技术能节省人工处理水力裂缝时间，提高效率。与之前简单的正交网络表征页岩复杂裂缝不同的是，该方法是在微地震监测数据的基础上，采取一定的简化等效（图4），根据微地震监测点的分布特征，将复杂裂缝表征为平面裂缝和正交缝网的综合，通过设置不同的导流能力来区分支撑剂的分布。

图3　正交裂缝网络示意

图4　结合微地震监测数据的平面缝和正交缝网

图5　体积压裂模拟方法模型

文献［32］基于双重孔隙连续介质模型，提出了体积压裂模拟方法（图5），该方法基于微地震监测结果，简化微地震事件为简单平面缝，裂缝可与井筒存在一定角度；设置裂缝中心为高导流区域，裂缝周围为水力压裂诱导改造区域，其传导能力介于中心裂缝与未改造区域之间，最外围为未改造区域，渗透率为基质渗透率，且传质因子较小。结合微地震监测结果使页岩储层改造区域的表征更接近实际情况，但是绝大多数井并未进行压后微地震监测，有学者就采用简化的理论模型开展了数值模拟工作。2011年，文献［33］系统地对比了单孔介质模型+平面缝/正交缝网、双孔介质系统+平面缝+水力压裂改造区（图6）和双孔介质系统+不规则压裂改造区，认为不同的模型均可以取得相似的历史拟合结果，但是模拟得到的泄气区域和压力场分布将存在差异，建议尽量综合微地震监测数据和地质数据准确估计压裂改造区域，从而更准确地模拟页岩气生产。

图6　平面缝及等效体积压裂改造区域模型

图7　页岩气复杂裂缝的线网模型

文献［34］、文献［35］和文献［36］提出了模拟页岩气复杂裂缝的线网模型，可以预测裂缝网络规模以及支撑剂在裂缝网络中的位置（图7）。裂缝网络的几何形状被假设为以注入点对称分布的椭圆形，椭圆范围内缝网由正交的裂缝表征，裂缝分别沿最大和最小主裂缝方向分布；不精细每条裂缝的具体参数，而注重椭球范围内水力裂缝的平均特征（如裂缝宽度、裂缝间距等）。该方法的不足之处在于裂缝网络模式不能与已有的天然裂缝直接衔接，不能模拟改造区微地震数据反映出裂缝网络的不对称性或裂缝网络不规则性。

3.2非常规数值模拟方法

（1）离散不规则裂缝网络模型文献［37］和文献［38］用双重介质模型对页岩气压裂水平井产能进行了模拟，用微地震响应确定改造体积区域，综合微地震事件、天然裂缝密度、水力压裂施工数据和生产数据，校准了水力裂缝密度分布，并用校准后的模型进行产量预测。借助三维地质模拟软件，有效减少了拟合工作和不确定性分析工作的耗时，既能进行单井规模的分析，也能开展油藏规模的模拟研究。图8a为微地震事件，图8b为离散不规则裂缝网络模型，图8c为基于离散不规则裂缝网络模型模拟的10年后压力波及区域。

文献［39］和文献［31］提出了综合水力裂缝扩展、微地震校正和油藏数值模拟的页岩气生产模拟技术。根据三维裂缝扩展软件得到水力压裂后的复杂裂缝网络，利用微地震监测数据对裂缝网络模型进行校正（图9a中的玫红色线条为校正后的模拟水力裂缝），最后采用非结构化网格自动生成技术划分网格，结合非均匀网格和混合网格对裂缝和油藏进行表征（图9b）。模型揭示了水力裂缝在天然裂缝发育的页岩储层中扩展的力学机制，实现水力裂缝形态的准确描述；考虑了网络裂缝中导流能力的不均匀分布，使模型更接近实际生产；同时网格自动生成技术的应用，节省了人工处理水力裂缝的时间，提高了模拟效率，该模型为页岩气产能的模拟提供了有力的支撑。

（2）有限元法-不规则裂缝模型有限元方法从20世纪60年代后陆续被用于研究油藏多孔介质渗流问题，而且由于其网格剖分灵活，处理复杂几何边界问题方便，在研究裂缝性多孔介质问题时受到学者们的青睐。针对常规天然裂缝性油藏，学者们提出了离散裂缝网络模型，并就模型中的渗流行为开展了大量研究工作。文献［40］将裂缝分为微裂缝（小于网格尺寸），中等裂缝（与计算网格相同）和大裂缝（在油藏中延伸较长）；将小裂缝和中等裂缝用一定的算法等效到基质渗透率中，大裂缝采用显式表征，不过这种单一介质模型处理裂缝和介质间交换存在不足。文献［41］和文献［42］结合裂缝性油藏地层中的真实裂缝信息，对裂缝实现更适当和可信的刻画；结合一系列的岩心或露头观测、测井数据等，基于方位、尺寸、空间位置和密度等对裂缝进行全方位描述，随机产生裂缝性油藏静态模型，并采用有限元渗流模型对裂缝系统的动态进行模拟。文献［43］提出了一个能适用于常规油藏模拟器的离散裂缝模型，考虑了裂缝和裂缝、基质和基质以及裂缝和基质间连通性，采用两点流量简化的非结构控制体积有限差分技术求解，应用该模型模拟了二维系统和一个复杂的三维裂缝系统渗流，模拟结果与有限差分模拟器结果吻合很好。常规裂缝性油藏虽然渗流机制与页岩气储层差别较大，但是其对于裂缝系统的相关研究对页岩气藏有很好的借鉴作用。

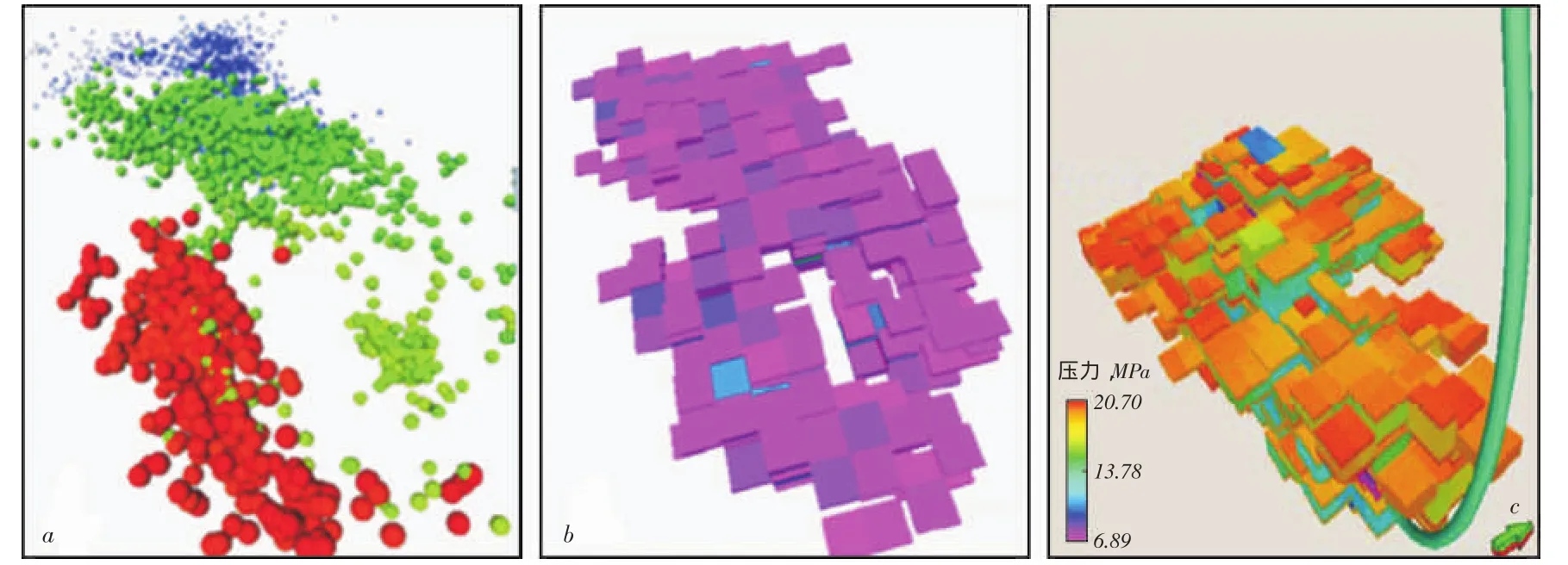
图8　基于双孔介质离散裂缝网络模型

图9　非结构化离散裂缝网络模型

近年来，学者开展了基于有限元的离散裂缝网络模型用于页岩气的探索。2012年，文献［44］采用扩展有限元方法研究了页岩气压裂水平井中的多尺度渗流问题。采用双孔双渗介质和离散裂缝表征页岩储层；离散裂缝不需要划分网格，可以分布于任意位置（图10a上图为网格划分及裂缝和基质单元的表征，图10a下图为模拟体积压裂水平井生产3年后压力分布）；考虑了岩石变形产生的渗透率应力敏感机制。文中对比了正交缝网和与斜交缝网开发效果，指出正交缝网效果更理想，压裂改造区域是控制压力衰减的关键因素。该模型能模拟页岩储层的离散裂缝网络，为压裂施工设计和产能优化提供了新的选择。2013年，文献［45］基于地球化学模拟器和离散裂缝特征，提出了新的提高煤层气采收率的模拟方法。文中指出，传统的煤层气模拟器来源于黑油模型或组分模型，均采用形状因子描述裂缝和基质间的交换，而形状因子只是裂缝间距的函数，忽略了裂缝的真实分布和连通性，文献［45］基于真实岩样建立离散裂缝网络模型，通过模拟拟稳态流求取岩样的形状因子，然后将该值应用于油藏规模的模拟；离散裂缝模型里考虑了大规模结构性裂缝和小规模割理缝。将吸附和解吸附等效成“化学反应”，模型由现有的地球化学模拟器扩展而来；最后应用该模型模拟了在含复杂裂缝系统煤层气储层中注CO2开采煤层气（图10b上图为网格划分和大裂缝空间分布，图10b为注气30 d后CO2浓度分布），讨论了裂缝渗透率敏感性。2014年，文献［46］应用离散裂缝网络模型研究了页岩气的渗流规律，提出了新的渗流数学模型：假设裂缝中流动符合立方定律，基质中流动符合非达西流特征（考虑解吸附、克努森扩散和滑脱），采用有限元方法求解模型，求解基于多物理场耦合求解器，裂缝随机生成；建立了含5条主水力裂缝和60条天然裂缝的页岩气水平井模型，并模拟了不同裂缝参数下的压力场分布及产量变化（图10c均为页岩气水平井压裂后生产1 000 d压力分布，水力裂缝渗透率相同，模型1的天然裂缝渗透率大于模型2）。

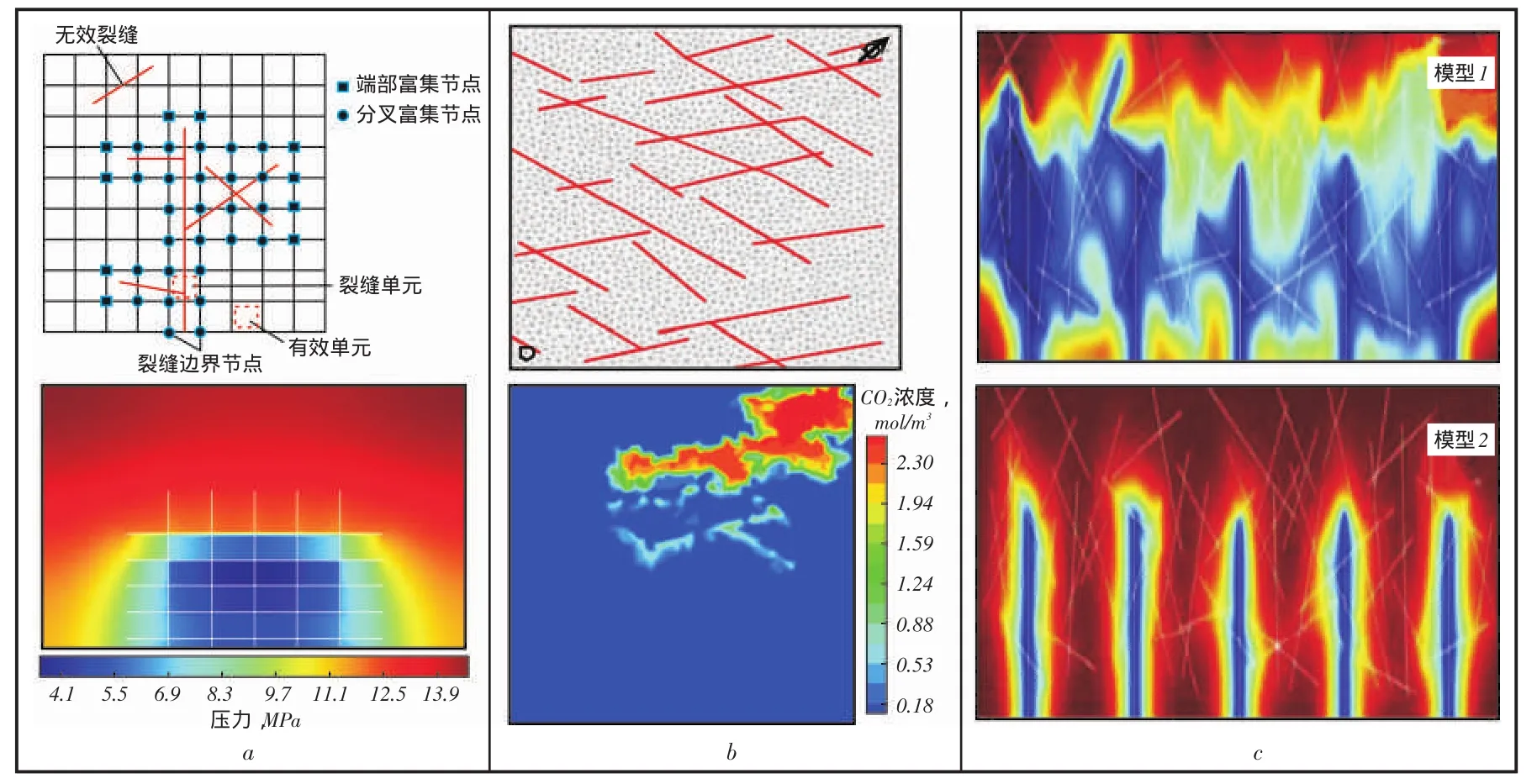
图10　基于有限元离散裂缝网络模型

4　结论

（1）页岩气经过几十年的规模开发，已形成相对成熟的地质评估和开发工艺技术，但是页岩气的生产仍缺乏有效的理论支撑。页岩孔喉复杂，天然裂缝发育，孔隙或裂缝尺度跨度大，渗流机制特别，建立既能耦合多尺度渗流规律，又可用于气藏规模的体积压裂水平井渗流模型是今后需要攻克的难题之一。

（2）试井模型可以分析页岩气多段压裂水平井流态特征，估算重要储层参数和裂缝参数，并根据校正后的参数预测产能；但是，试井分析方法存在许多不足。模型往往是基于很多简化的假设，如裂缝垂直于井筒、假定储层改造范围为规则的立方体区域、未考虑解吸附或者纳米级尺度下的渗流规律等，与实际页岩气藏存在较大差异；而且解吸附、水力裂缝等因素为模型求解增加了难度，诸多不足制约着该方法的应用。

（3）天然裂缝和水力裂缝的精细描述和表征是页岩气数值模拟的关键技术。常规的数值模拟方法采用双孔介质模拟天然裂缝，采用板状缝或者正交裂缝网络模拟水力裂缝，该方法不能反映页岩储层大型水力压裂后缝网的不规则性，难以正确模拟页岩气井生产特征。结合微地震监测、测井数据和施工数据等建立的离散裂缝网络模型能更准确刻画压裂后裂缝网络特征，是未来页岩气数值模拟的发展趋势。

（4）有限元方法网格剖分灵活，处理复杂边界问题方便，模拟页岩储层的复杂网络的比有限差分方法更具优势；同时，有限元方法在力学分析中发展成熟，结合其他方法能模拟页岩储层中复杂裂缝扩展；有限元方法能成为裂缝扩展和产能模拟的结合点，为页岩气体积压裂水平井模拟提供了新的思路。

［1］邹才能，董大忠，杨桦，等.中国页岩气形成条件及勘探实践［J］.天然气工业，2011，31（12）：26-39.

Zou Caineng，Dong Dazhong，Yang Hua，et al.Conditions ofshale gas accumulation and exploration practices in China［J］.Natural Gas Industry，2011，31（12）：26-39.

［2］邹才能，董大忠，王社教，等.中国页岩气形成机理、地质特征及资源潜力［J］.石油勘探与开发，2010，37（6）：641-653.

Zou Caineng，Dong Dazhong，Wang Shejiao，etal.Geological charac⁃teristics，formationmechanism and resource potential ofshale gas in China［J］.Petroleum Exploration and Development，2010，37（6）：641-653.

［3］董大忠，邹才能，杨桦，等.中国页岩气勘探开发进展与发展前景［J］.石油学报，2012，33（1）：107-114.

Dong Dazhong，Zou Caineng，Yang Hua，et al.Progress and pros⁃pects of shale gas exploration and development in China［J］.Acta PetroleiSinica，2012，33（1）：107-114.

［4］Hill D G，Nelson CR.Gas productive fractured shales：an overview and update［J］.Gas Tips，2000，6（3）：4-13.

［5］魏明强，段永刚，方全堂，等.页岩气藏孔渗结构特征和渗流机理研究现状［J］.油气藏评价与开发，2011，1（4）：73-77.

WeiMingqiang，Duan Yonggang，Fang Quantang，et al.Current re⁃search situation ofporosity&permeability characteristics and seep⁃agemechanism of shale gas reservoir［J］.Reservoir Evaluation andDevelopment，2011，1（4）：73-77.

［6］ElgmatiM.Shale gas rock characterization and 3D submicron pore network reconstruction［D］.Rolla：Missouri University of Science and Technology，2011.

［7］Loucks RG，Reed RM，Ruppel SC，etal.Morphology，genesis，and distribution ofnanometer⁃scale pores in siliceousmudstones of the Mississippian Barnett shale［J］.Journal of Sedimentary Research，2009，79（12）：848-861.

［8］Swami V，Clarkson CR，Settari A，et al.Non⁃Darcy flow in shale nanopores：dowe have a finalanswer?［R］.SPE 162665，2012.

［9］Sampath CW，Keighin K.Factors affecting gas slippage in tight sandstones［J］.JournalofPetroleum Technology，1982，34（5）：2 715-2 720.

［10］Florence FA，Rushing JA，Newsham K E.Improved permeability prediction relations for low⁃permeability sands［R］.SPE 107954，2007.

［11］Ertekin T，KingGR，SchwererFC.Dynamic gasslippage：aunique dual⁃mechanism approach to the flow of gas in tight formations［R］.SPE 12045-PA，1986.

［12］Sakhaee⁃Pour A，Bryant S L.Gas permeability of shale［R］.SPE 146944-PA，2012.

［13］Ziarani A S，Aguilera R.Knudsen’s permeability correction for tight porousmedia［J］.Transport in Porous Media，2012，91（1）：239-260.

［14］Javadpour F.Nanopores and apparent permeability ofgas flow in mudrocks（shales and siltstone）［J］.Journal of Canadian Petro⁃leum Technology，2009，48（8）：16-21.

［15］Kucuk F，SawyerW K.Transient flow in naturally fractured reser⁃voirs and its application to Devonian gas shales［R］.SPE 9397，1980.

［16］Carlson E S，Mercer JC.Devonian shale gas production：mecha⁃nisms and simple models［J］.Journal of Petroleum Technology，1991，43（4）：476-482.

［17］Aboaba A，Cheng Y.Estimation offracturepropertiesforahorizontal wellwithmultiplehydraulic fractures in gasshale［R］.SPE 138524，2010.

［18］Bello R O，Watenbargen R A.Multi⁃stage hydraulically fractured horizontal shale gaswell rate transient analysis［R］.SPE 126754，2010.

［19］Al⁃AhmadiH A，Almarzooq AM，Watenbargen R A.Application of linearflow analysis to shale gaswells⁃field cases［R］.SPE 130370，2010.

［20］Brohi I，Pooladi⁃Darvish M，Aguilera R.Modeling fractured hori⁃zontal wells as dual porosity composite reservoirs⁃application to tightgas，shale gasand tightoilcases［R］.SPE 144057，2011.

［21］Ozkan E，Brown M，Raghavan R，et al.Comparison offractured⁃horizontalwell performance in tight sand and shale reservoirs［J］. SPEReservoirEvaluation&Engineering，2011，14（2）：248-259.

［22］Song B，Michael J，Christine E E.Design ofmultiple transverse fracture horizontalwells in shale gas reservoirs［R］.SPE 140555，2011.

［23］Song B，Christine EE.Rate⁃normalized pressure analysisfordeter⁃mination ofshale gaswellperformance［R］.SPE 144031，2011.

［24］Orkhan S，Hasan A，Ai⁃Ahmadi，et al.A semi⁃analyticmethod for historymatching fractured shale gas reservoirs［R］.SPE 144583，2011.

［25］Freeman CM，Moridis G，Ilk D，etal.A numerical study ofperfor⁃mance for tightgas and shale gas reservoirs systems［J］.Journal of Petroleum Science and Engineering，2013，108：22-29.

［26］Wang H T.Performance ofmultiple fractured horizontal wells in shale gas reservoirswith consideration ofmultiplemechanisms［J］. JournalofHydrology，2014，510：299-312.

［27］Maxwell SC，SteinsbergerN，Zinno R.Microseismic imaging ofhy⁃draulic fracture complexity in the Barnett Shale［R］.SPE 77440，2002.

［28］FisherM K，Wright CA，Davidson BM，etal.Integrating fracture mapping technologies to optimize stimulations in the Barnett shale［R］.SPE 77441，2002.

［29］WarpinskiN R，Kramm R C，Heinze JR，et al.Comparison ofsin⁃gle⁃and dual⁃array microseismic mapping techniques in the Bar⁃nettshale［R］.SPE 95568，2005.

［30］Cipolla，Lolon，Mayerhofer.Reservoir modeling and production evaluation in shale⁃gasreservoirs［R］.IPTC 13185，2009.

［31］Cipolla，Fitzpatrick，Williams，etal.Seismic⁃to⁃simulation forun⁃conventionalreservoirdevelopment［R］.SPE 146876，2011.

［32］Arvind，Franz D，Martin C，et al.Volumetric fracturemodeling ap⁃proach（VFMA）：incorporatingmicroseismic data in the simulation ofshale gasreservoirs［R］.SPE 134683，2010.

［33］James L，Mike D，Xu Z.Critical evaluation ofshale gas reservoir simulation approaches:single⁃porosity and dual⁃porositymodeling［R］.SPE 141756，2011.

［34］MayerhoferM J，Lolon.Integration ofmicroseismic fracture map⁃ping results with numerical fracture network production modeling in the Barnettshale［R］.SPE 102103，2006.

［35］XuW Y，Marc T，IanW.Characterization ofhydraulically⁃induced shale fracture network using an analytical/semi⁃analytical model［R］.SPE 124697，2009.

［36］XuW Y，Thiercelin M.Wiremesh：a novel shale fracture simulator［R］.SPE 132218，2010.

［37］Du C，Zhang X，Melton B，etal.A workflow for integrated Barnett Shale gas reservoirmodeling and simulation［R］.SPE 122934，2009.

［38］Du C，Zhang X，Zhan L，et al.Modeling hydraulic fracturing in⁃duced fracture networks in shale gas reservoirs as a dual porosity system［R］.SPE 132180，2010.

［39］Weng XW，Olga K，Dimitry C，et al.Applying complex fracture model and integrated workflow in unconventional reservoirs［J］. JournalofPetroleum Scienceand Engineering，2014，124：468-483.

［40］Lee SH，Durlofsky L J，Lough M F，etal.Finite difference simula⁃tion of geologically complex reservoirs with tensor permeabilities［R］.SPE 52637，1997.

［41］Lee SH，Jensen CL，Lough M F.An efficientfinite differencemod⁃el for flow in a reservoirwith multiple length⁃scale fractures［R］. SPE 56752，1999.

［42］Sarda S，Jeannin L，Bourbiaux B.Hydraulic characterization of fractured reservoirs：simulation on discrete fracture models［R］. SPE 66398，2001.

［43］Karimi⁃Fard M，Durlofsky L J，Aziz K.An efficient discrete⁃frac⁃turemodelapplicable forgeneral⁃purpose reservoirsimulators［R］. SPE 88812，2003.

［44］ShengM，LiG，Shah SN，etal.Extended finite elementmodeling of multi⁃scale flow in fractured shale gasreservoirs［R］.SPE 159919，2012.

［45］Gong B，Zhang Y，Fan Y，et al.A novel approach to model en⁃hanced coal bedmethane recoverywith discrete fracture character⁃izations in a geochemical simulator［J］.Journal of Petroleum Sci⁃ence and Engineering，2013，124：198-208.

［46］Mi L D，Jiang H Q，Li JJ，et al.The investigation offracture aper⁃ture effect on shale gas transportusing discrete fracturemodel［J］. JournalofNaturalGasScienceand Engineering，2014，21：631-635.

AdvancesofSimulation StudiesofVolum etric Fracturing HorizontalW ell Productivity for Shale GasReservoir

ZHOUXiang,ZHANGShicheng,MA Xinfang,ZHANGYe
（SchoolofPetroleum Engineering,China University ofPetroleum,Beijing 102249,China）

Shale gas reservoir is characterized by nanoscale porosity and ultra⁃low permeability,which usually has no naturalproductivity, and has to be economically developed bymeans ofhorizontalwelland volumetric fracturing technology.The study on shale gasathome and abroadmostly focused on geological characteristic evaluation and developmentprocess technologies,with few theoretical approaches to its productivity by volumetric fracturing horizontal drilling process.The key to shale gas production research should be in exactdescription of multiple scale flow mechanism and fine characterization ofcomplex hydraulic fracture networks.Through wide investigation and analyses, this paper discusses such a flow mechanism,reviews themodel formultiple transverse fracture horizontalwell test in shale gas reservoir, elaborates how to distinguish flow regimes and evaluate reservoirand fracture parameters according to differentmodels,and systematically introduces themethods ofnumerical simulation for shale gas,including conventionalnumericalmodeling,discrete fracture networkmodel⁃ing and finite element approaches.It is believed that the discrete fracture network modeling and finite elementapproacheswill be the fu⁃ture research trend fornumericalsimulation ofshale gasproductivity.

shale gas;volumetric fracturing;horizontalwell;productivity

TE375

A

1001-3873（2015）05-0612-08

10.7657/XJPG20150522

2015-04-24

2015-07-31

国家科技重大专项（2012ZX05018-004）

周祥（1987-），男，湖南岳阳人，博士研究生，油气田开发，（Tel）18611725512（E-mail）xiang_zhou2008@sina.com.