基于变窗函数谱重排的谱分解技术

崔震，曹思远，刘伟，马媛媛（中国石油大学a.油气资源与探测国家重点实验室；b.CNPC物探重点实验室，北京102249）

基于变窗函数谱重排的谱分解技术

崔震，曹思远，刘伟，马媛媛
（中国石油大学a.油气资源与探测国家重点实验室；b.CNPC物探重点实验室，北京102249）

谱分解是将地震信号由时间域变换到时间—频率域，然后再对其局部时频属性和瞬时频率特性进行分析的技术。常规谱分解方法受Heisenberg准则限制，不能同时兼顾时间分辨率和频率分辨率，时频谱重排有效规避了Heisenberg准则的限制，同时提高了时频谱的聚集性，且对噪音等干扰聚焦。变窗函数谱重排算法是在常规时频谱重排的基础上，利用Hermite窗的正交性和可递推性，得到多个变化窗口的谱重排结果，然后利用最小二乘估计原理，对多个谱重排剖面进行加权近似组合。合成记录和实际例子均表明该方法在保证了时频谱高聚焦性的同时，分散了噪音干扰，能准确归位时频能量的真实位置，对低频阴影有很好的显示效果。

谱分解；Hermite窗函数；变窗口；谱重排；加权组合

谱分解技术在地震数据处理中应用十分广泛。文献［1］发现在油气储集层下方存在低频伴影现象；文献［2］总结了产生低频阴影区的至少10个原因；文献［3］将短时傅里叶变换引入油气勘探领域，对频率的横向变化进行定量描述，产生了最初的地震谱分解技术。随着时频分析技术的不断发展，谱分解也向高精度、高保真度方向发展，目前已经广泛应用于油气检测、河道检测、断裂解释、AVO分析等方面[4-6]。

时频分析技术是谱分解的基本手段，文献［7］提出以高斯函数为线函数构建基函数，将一维时间信号映射为二维时频变信号。文献［8］提出短时傅里叶变换（Short Time Fourier Transform，STFT），使用固定时窗分析局部时间的频率成分，但是无法兼顾时间和频率的分辨率。伽柏变换是使用高斯窗的一种特殊的短时傅里叶变换，由于高斯窗的特性，使得它具有短时傅里叶变换的所有性质，并且在一定程度上兼顾了时间和频率分辨率[9]。文献［10］提出的连续小波变换对于非平稳信号的刻画有了很大的改善，其窗函数的宽度随频率变化，在高频时使用窄窗，在低频时使用宽窗，这样就可以用不同的分辨率来分析信号，相对于短时傅里叶变换，小波变换具有更好的能量聚集性和多分辨率特征。文献［11］S变换时频分析方法，其基于滑动高斯窗函数，同时具有傅里叶变换和小波变换的优点。

文献［12］提出了时频谱重排的思想，主要应用在非平稳信号的分析中。文献［13］重新解释了谱重排的实际含义，把谱重排看成一个时频分布的反平滑过程。时频重排谱对信号具有更好的局部刻画能力，能够把原始谱中的每一个点的时频能量集中到信号的瞬时频率和延迟时的位置。前人的研究主要集中在信号分析领域方面，在地球物理领域的研究相对较少。时频谱重排能够生成聚焦的时频分布，同时也对随机噪音能量聚焦，文献［14］提出多窗口重排方法，对于信号的抖动具有更好的稳定性。本文将变窗口思想与时频谱重排相结合，选取正交Hermite函数作为窗函数，得到了时频分辨率较高的时频分布，同时压制了噪音的能量。

1　方法原理

1.1时频重排原理

时频谱重排是在原有频谱的基础上进行能量重新分配，提高谱图的时频聚集性，使得时频定位准确度提高。由于伽柏谱图在一定程度上兼顾时间分辨率和频率分辨率，可以为重排提供较好的基础。伽柏时窗内的时频振幅谱可以定义为地震信号振幅谱和高斯窗函数的振幅谱的乘积：

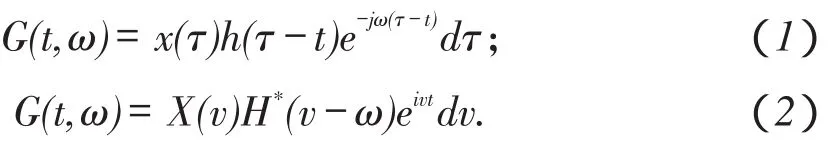
高斯窗h(t)=exp(-t2/2σ)/ 2πσ，固定σ后，根据Heisenberg测不准准则，窗口大小固定为，则由（1）式和（2）式可以看出，伽柏谱即是用的时频窗，分别在时间和频率方向对真实点谱的平滑。

文献［15］根据时频谱窗函数与真实点谱的关系，提出谱重排算法，其目的是将伽柏谱中每一个时频点处的能量进行移动，使其聚集在二维高斯窗内，谱能量的重心处即为真实谱坐标点，从而规避了Heisenberg测不准准则，提高了时频分辨率。由文献［15］提出的谱能量重排算法可以得到：

任意点(t',f')的值是所有重排到这一点的点(t,f)值的和：

1.2多窗口统计方法

在计算中，时频分析实际上是对无限长平稳信号序列的截断，这种截断效应往往使谱图分辨率降低。针对这一现象，文献［14］在发现多个正交窗口的组合可以削弱这种截断效应的基础上提出了多窗口方法，利用多个正交窗口{hk(t)，k∈N}获得独立的近似功率谱估计，综合统计这些近似估计，最终得到平稳信号功率谱估计，即

文献［16］则将其推广到时频域：

1.3改进的时频重排

由于谱重排是谱图平滑的逆过程，相比于普通的谱图，谱重排对平稳谱的截断效果更加明显。从（6）式的分析可以看出，多窗口加权可以压制畸变，重新得到稳定的光滑谱，与原谱图相比具有更高的聚焦性。

1.3.1Hermite窗函数

为了得到平稳信号谱估计，要求多窗口的选取为正交函数，其时频分布近似椭圆或圆形分布，由于Hermite函数是正交函数，其时频聚集性好，能够较好地刻画大多数非平稳信号[17]，而且在计算过程中可以通过递推方式减少计算量，因此选择Hermite函数作为窗口函数进行时频谱重排。

k阶Hermite函数表示为

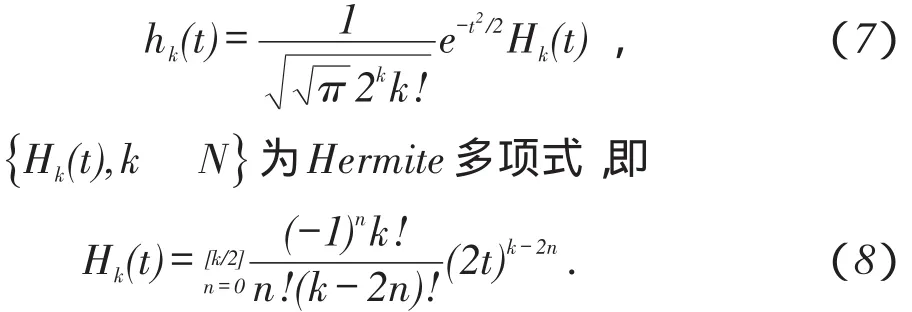
由（3）式可以看出，计算过程中需要对th（t）和dh（t）/dt进行多次迭代，为此，对dh（t）/dt化简得到递推关系式以减少计算量：

1.3.2变窗统计组合

利用不同阶数Hermite窗口函数按照（3）式进行时频谱重排，可以得到多个窗口聚焦时频谱，即变窗口谱重排（Multiple Window Reassigned Spectrum，MWRS），对这些谱进行统计组合，即

估算系数dk利用最小二乘法计算：

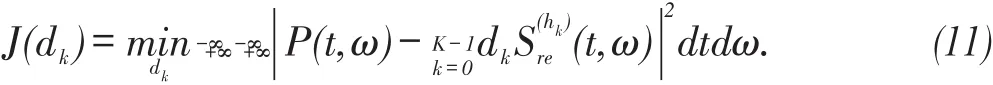
离散化得到矩阵形式：

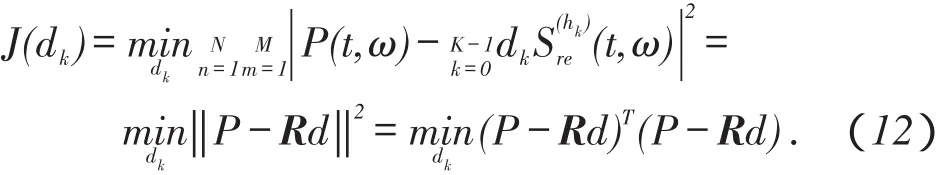
对（12）式中dk求导，令

求解得

这样得到加权估计系数dk，对P的最小二乘估计为

其物理意义是利用反演的方法，寻找多窗口谱图重排的最优组合。

2　模型测试

图1a中的信号由50Hz雷克子波、50Hz90°相移雷克子波、20Hz 180°相移雷克子波和2个时间相近的30Hz雷克子波构成。分别对该信号进行伽柏变换，伽柏谱重排（图1c）和变窗口谱重排，可以看出，与伽柏谱（图1b）相比，伽柏重排谱（图1c）时频聚集性有较大提升，时频分辨率都有所提高，然而仔细查看不难发现，伽柏重排谱中产生了多个亮点（谱放大区域），这是谱重排截断效应引起的，而且对于距离较近的子波其时频谱会出现相互干涉，无法准确指示频率的真实位置（红色区域）。变窗口谱重排（图1d）在保证较高时频聚集性的同时克服了多个极值的问题，能准确指示频率的真实位置，且能很好地区分距离相近的子波。

图2是在图1信号的基础上加入高斯噪音之后进行时频分析的结果，不难看出，伽柏谱重排对一些随机噪音能量进行了聚焦，变窗谱重排在保证较高的时频分辨率的同时，对噪音能量也有很好的压制作用。图3是在实际地震资料中抽取单道数据的时频分析结果，变窗口重排谱具有更高的时频分辨率，且对噪声也有较好的压制，低频阴影现象突出明显。

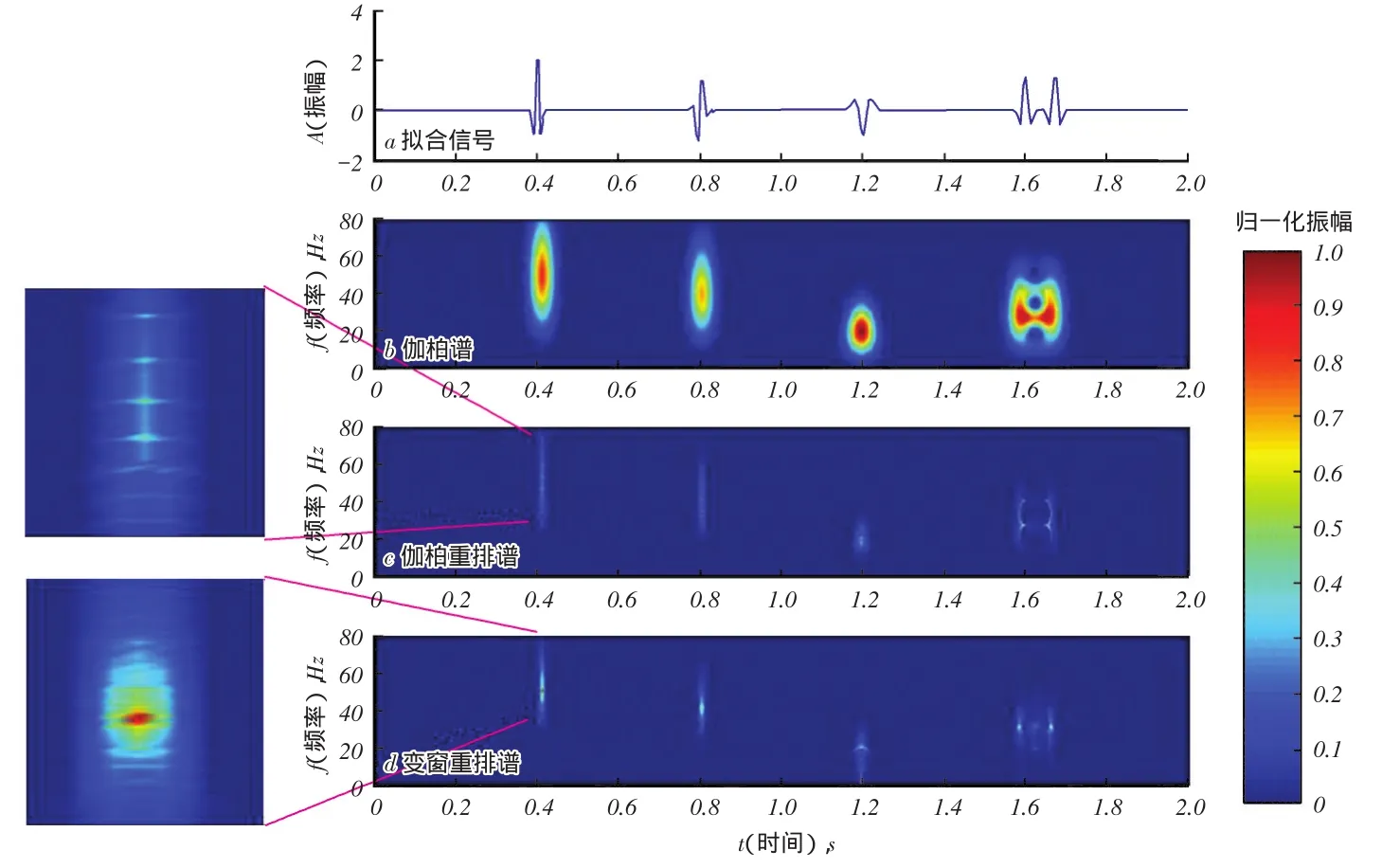
图1　合成地震记录时频分析结果

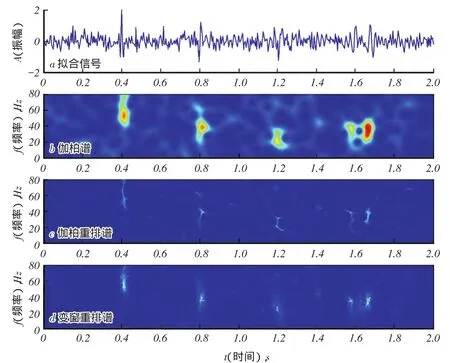
图2　含噪合成地震记录时频分析结果

3　实例

由于大地滤波和吸收衰减作用，地震波频谱呈现非平稳性，低频阴影现象就是非平稳性之一。低频阴影是在含油气层下方出现的低频强能量区域，该区域高频能量则比较弱[18]。这一特性常被用来探测含气储集层，在低频剖面上含气储集层下方出现高亮能量团，随着谱分解剖面频率增加，亮度削弱直到消失。

图4为新疆某地区地震叠后剖面，声波时差测井曲线表明，在该位置速度保持低位，为高储含气层，与钻井结果相吻合。利用常规伽柏变换和变窗谱重排分别对整个剖面进行谱分解，分别截取伽柏谱数据体和变窗重排谱数据体的20 Hz频率切片如图5a和图5b所示。由图5可见，由于伽柏谱时频分辨率过低，能量团上下延时接近0.1 s，影响了目的层的精确定位，而变窗重排谱时频分辨率较高，能够准确刻画目的层位置，并且可以清晰判别能量展布。

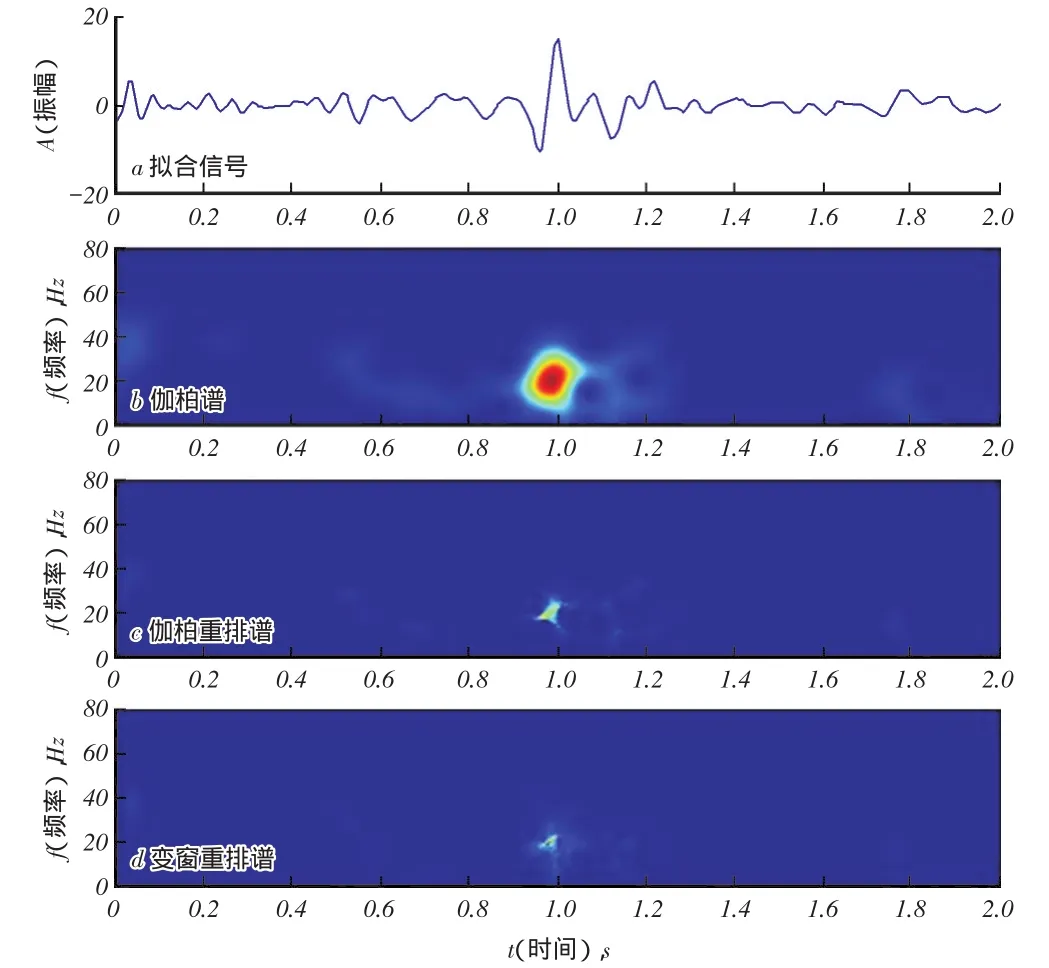
图3　单道实际记录时频分析结果

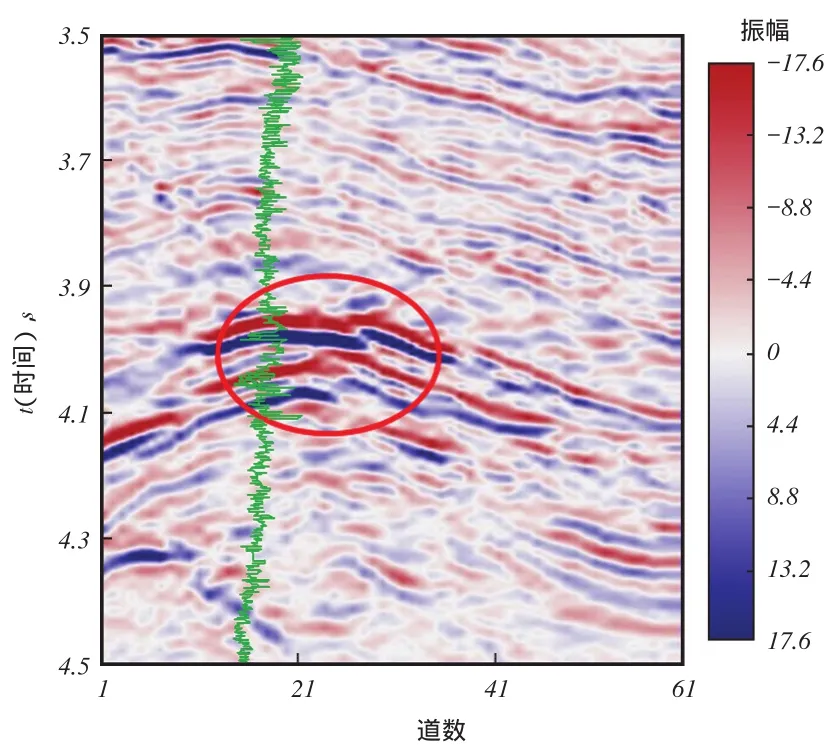
图4　实际含气地震剖面（红色区域为含气储集层）

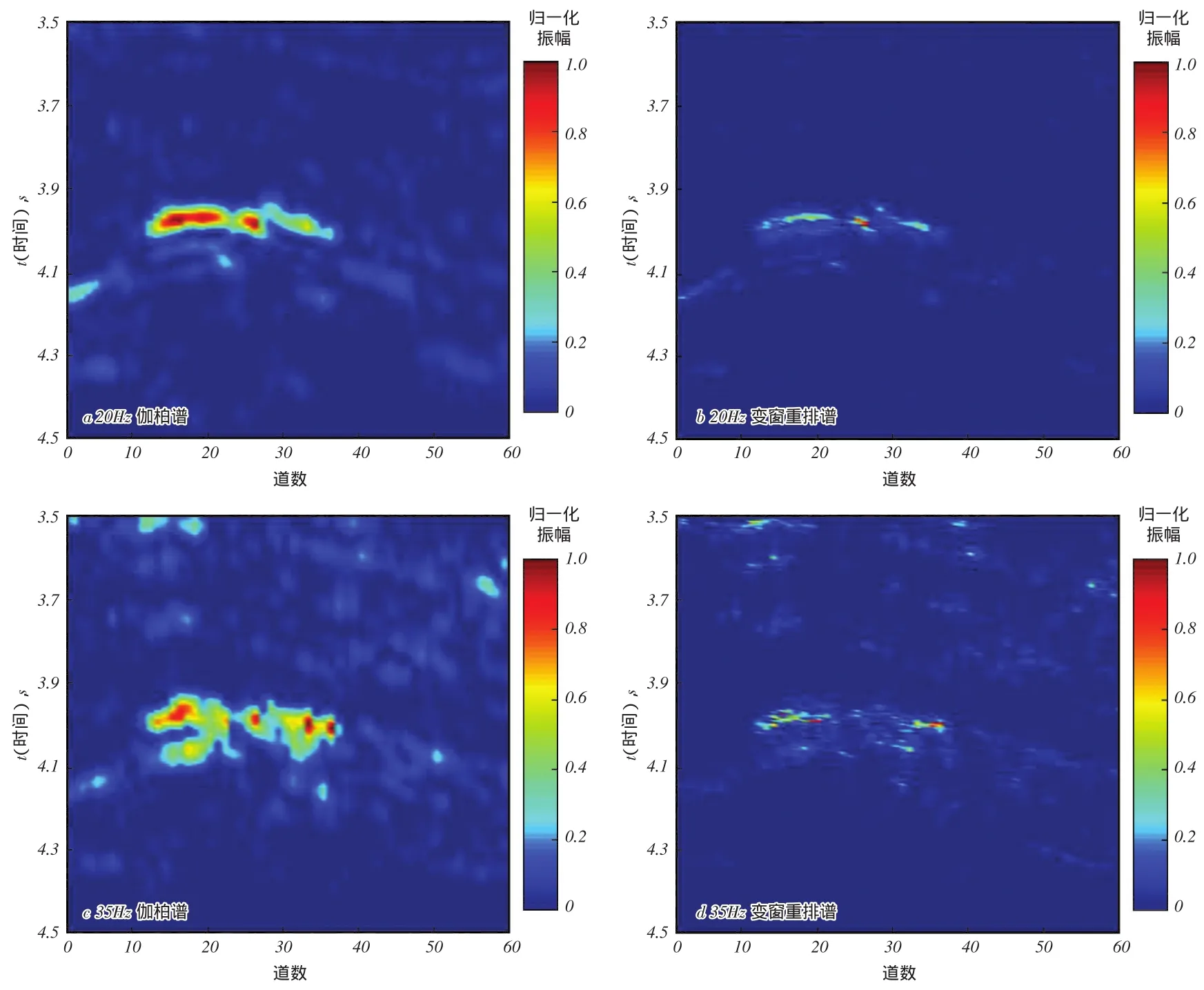
图5　频率切片对比

图5c和图5d分别为截取伽柏谱数据体和变窗重排谱数据体的35Hz频率切片。从图5可以看出，随着频率增加，能量逐渐减弱，变窗重排谱相较伽柏谱时频分辨率更高，能够更加准确刻画目的层位置。此外，变窗重排谱对低频阴影现象的敏感度要明显高于伽柏谱，是一种实用的地震记录谱分解方法。

4　结论

本文在常规伽柏时频分析方法的基础上，讨论了伽柏谱重排的优点，同时指出了其对于信号能量收敛聚焦的不稳定性，结合多窗口压制不稳定震荡的优点，提出了变窗口谱重排法，该方法利用多阶Hermite函数作为窗函数进行时频谱重排，通过最小二乘原理对其加权组合得到稳定的高分辨率时频谱。通过对合成数据和实际资料处理，可以看出变窗口谱重排相对于常规的伽柏变换和伽柏谱重排具有更高的时频分辨率，同时对噪声也有一定的压制效果。

符号注释

［1］TanerM T，Koehler F，SheriffR E.Complex seismic trace analysis［J］.Geophysics，1979，44（6）：1 041-1 063.

［2］Ebrom D.The low⁃frequency gas shadow on seismic sections［J］.The Leading Edge，2004，23（8）：772.

［3］Partyka G，Gridley J，Lopez J.Interpretational applications ofspec⁃tral decomposition in reservoir characterization［J］.The Leading Edge，1999，18（3）:353-360.

［4］MarfurtK J，Kirlin R L.Narrow⁃band spectralanalysisand thin⁃bed tuning［J］.Geophysics，2001，66（4）：1 274-1 283.

［5］Prasad R，DawwasM，Tanoli S.Detecting channelsands using spec⁃traldecomposition on 3⁃D seismic data:a case study［R］.EAGEDe⁃tective Stories Behind Prospect Generation Workshop⁃Challenges and theWay Forward，2009.

［6］Wei X D.Interpretational applications ofspectral decomposition in identifyingminor faults［R］.72nd EAGE Conference&Exhibition. Barcelona，2010.

［7］GaborD.Theory ofcommunication.Part 1:the analysis ofinforma⁃tion［J］.Journal of the Institution ofElectrical Engineers-PartⅢ：Radio and Communication Engineering，1946，93（26）：429-441.

［8］Potter R K，Kopp G A，Kopp H G.Visible speech［M］.New York: DoverPublications Inc.，1947.

［9］周家雄，张国栋，尚帅.基于重排Gabor变换的高分辨率谱分解［J］.世界地质，2013，32（1）：153-157.

Zhou Jiaxiong，Zhang Guodong，Shang Shuai.High⁃resolution spec⁃trum decomposition based on reassigned Gabor transform［J］.World Geology，2013，32（1）：153-157.

［10］Morlet J，Arens G，Fourgeau E，etal.Wave propagation and sam⁃pling theory—PartⅠ：complex signaland scattering inmultilayered media［J］.Geophysics，1982，47（2）：203-221.

［11］周怀来，李录明.广义S变换在地震信号特征信息提取中的应用［J］.新疆石油地质，2008，29（6）：758-760.

Zhou Huailai，Li Luming.Application ofgeneralized S⁃transform to extraction ofseismic signal characteristic information［J］.Xinjiang Petroleum Geology，2008，29（6）：758-760.

［12］Kodera K，De Villedary C，Gendrin R.A new method for the nu⁃merical analysis ofnon⁃stationary signals［J］.Physics of the Earth and Planetary Interiors，1976，12（2）：142-150.

［13］Auger F，Flandrin P.Improving the readability of time⁃frequency and time⁃scale representationsby the reassignmentmethod［J］.Sig⁃nal Processing，1995，43（5）：1 068-1 089.

［14］Thomson D J.Spectrum estimation and harmonic analysis［J］.Pro⁃ceedings ofthe IEEE，1982，70（9）：1 055-1 096.

［15］Flandrin P，Auger F，Chassande⁃Mottin E.Applications in time⁃fre⁃quency signalprocessing［M］.Arizona：CRCPress，2003.

［16］Bayram M.Multiplewindow time⁃frequency analysis［D］.Houston：Rice University，1996.

［17］丁夏畦，丁毅.Hermite展开与广义函数［M］.武汉：华中师范大学出版社，2005.

Ding Xiagui，Ding Yi.Hermite expansion and generalized functions［M］.Wuhan:Huazhong NormalUniversity Press，2005.

［18］张波，王真理，周水生.谱分解在含气检测中的应用［J］.地球物理学进展，2010，25（4）：1 360-1 364.

Zhang Bo，Wang Zhenli，Zhou Shuisheng.Application ofspectrum decomposition to gas detection［J］.Progress in Geophysics，2010，25（4）：1 360-1 364.

SpectralDecomposition Technology Based on M ultipleW indowsReassigned Spectrum

CUIZhen,CAOSiyuan,LIUWei,MA Yuanyuan

(China University ofPetroleum,a.State Key Laboratory ofPetroleum Resource and Prospecting; b.CNPCKey Lab ofGeophysics Exploration,Beijing 102249,China)

Spectral decomposition decomposes a time domain signal to the time⁃frequency domain,which can characterize the local time⁃frequency properties and instantaneous frequency.The time⁃frequency resolution of conventional spectral decomposition methods is not high due to Heisenberg uncertainty principle.The reassigned spectrum method avoids the Heisenberg uncertainty principle and the time⁃frequency resolution is increased.Besides,italso generates concentrated energy for random noise.Themultiple windows reassigned spec⁃trum is based on reassigned spectrum and gets reassigned spectrums using orthogonality and recurrence.At last,the reassigned spectrums are distributed by theweighted value based on least square estimation.Synthetic data and field data show that the proposed approach can gethigh time⁃frequency resolution and disperse the random noise;meanwhile the realposition oftime⁃frequency energy can be located and indicates the low⁃frequency shadow related with hydrocarbon effectively.

spectraldecomposition;Hermitewindow function;multiplewindows;reassigned spectrum;weighted value combination

P631.445

A

1001-3873（2015）05-0602-05

10.7657/XJPG20150520

2014-12-20

2015-05-22

国家科技重大专项（2011ZX05024-001-01）

崔震（1991-），男，河北沧州人，硕士研究生，地震资料处理，（Tel）18810906151（E-mail）761683429@qq.com.