技术进步偏向与中国地区经济波动

邓 明



技术进步偏向与中国地区经济波动

邓 明

（厦门大学经济学院 福建厦门 361005）

技术冲击对经济波动的影响不仅仅体现在技术进步速率上，还可能体现在技术进步的偏向性上。基于1990-2010年中国省际面板数据，本文构建空间动态面板数据模型实证研究了技术进步的偏向程度对中国地区经济波动的影响。研究结果表明，中国大部分省份技术进步方向偏向于资本，而资本偏向的技术进步则显著强化了经济波动，即使改变度量经济波动的方式，这一结果也是稳健的。与其相对应的是，基于全要素生产率构建的技术冲击变量对经济波动反而没有显著影响。由此可见，技术冲击对经济波动的短期影响更多依赖于技术进步的方向而非速率。

技术进步偏向 经济波动 空间动态面板数据模型

一、问题提出

发展是硬道理，但是能够平稳的发展，对于中国这样一个13亿人口的发展中大国而言具有特别重要的意义，改革开放30多年来中国的经济增长虽然高速，但也并非是绝对平稳的，如果以真实GDP增长率的波动来衡量我国经济的波动，那么我国的经济波动呈现一个重要的特征，即波动的幅度在1994年前后发生了较大的变化：1994年之前波动幅度较大，大起大落；而1994年之后出现了波幅明显减小，波动平缓的情况。因此，寻求稳定经济增长的政策手段在当前中国经济面临结构调整、经济增速已明显放缓的关键时期显得尤为重要。

20世纪70年代以前，几乎所有的经济学家都用“需求冲击理论”来解释经济周期产生的根源，认为经济周期根源于总需求变动的需求面冲击，但是，1973-1974年的石油危机，使经济学家们意识到供给对总产量的决定也很重要。之后，新古典宏观经济学的代表人物卢卡斯和萨金特等人提出了货币商业周期理论。他们认为货币供给的冲击即货币存量的随机变动会引起经济波动。

从20世纪80年代开始，一些经济学家对经济波动根源的研究视角开始转向实际因素，试图用实际因素去解释经济周期波动的根源，诞生了构成新古典宏观经济学核心的“实际周期理论”。以基德兰德和普利斯科特（Kydland和Prescott，1982）为代表的“实际经济周期理论”认为，经济周期波动的根源是实际因素，其中特别值得注意的是技术冲击，这种冲击决定了投入（资本与劳动）转变为产出的能力，引起了产出与就业的波动。

大量研究也考察了技术进步与技术冲击对中国经济周期与经济波动的影响。简泽（2005）利用结构性向量自回归模型分析了技术冲击对中国经济波动的影响，发现技术冲击使得实际GDP、投资和消费呈现波动的典型特征，并解释了绝大多数的消费波动、一到四年内产出波动的37%到56%以及投资波动的五分之一到三分之一。黄赜琳（2006）通过构建了一个可分劳动RBC模型、从供给角度考察了技术冲击对中国经济波动的影响，技术冲击可以解释中国经济波动的主要部分，而且技术进步对改革后的产出、居民消费和就业都产生了正向冲击效应。徐舒等人（2011）本文在动态随机一般均衡模型（DSGE）的理论框架下建立了一个内生R&D投入与技术转化模型，研究了技术扩散对我国经济波动的影响，发现相对于中性技术冲击而言，技术扩散冲击在长期中使产出和技术存量处在更高的均衡水平上。

但是，现有文献关于技术冲击与经济波动之间的研究仅仅讨论了技术进步水平的外生冲击对经济波动的影响；而事实上，技术进步对于经济波动的作用不仅仅体现在技术进步水平或是速度上，还体现在技术进步的方向上。技术进步方向关注的是技术进步对各种生产要素边际产出的相对影响。关于技术进步方向的研究始于80多年前，希克斯（Hicks，1932）基于劳动与资本两个要素，将技术进步分成三个方向：如果技术进步更有助于提高劳动的边际产出，则称技术进步偏向于劳动力；如果更有助于提高资本的边际产出，则称技术进步偏向于资本；如果对劳动与资本边际产出之比没有影响，则称技术进步是中性的。以阿西莫格鲁（Acemoglu, 2002, 2007）为代表的一系列研究则将技术进步方向扩展到任意投入要素之间，并对技术进步方向进行了重新定义：如果技术进步更有助于提高某种要素（Z）的边际产出，称之为偏向Z的技术进步（Z-biased technical change）。戴维和克伦德特（David和Klundert, 1965）是最早实证分析技术进步方向的文献之一，他们利用美国1899-1960年的数据，估计了劳动与资本的替代弹性以及劳动效率与资本效率的增长率，发现美国1899-1960年的技术进步总体上偏向资本。威尔金森（Wilkinson, 1968）、派尼克（Panik, 1976）等人的研究也得出大致相同的结论：美国二十世纪以来的技术进步总体上偏向资本。戴天仕和徐现祥（2010）、邓明（2014）分别基于中国年度时间序列数据和地区层面的面板数据考察了中国的技术进步方向，均认为中国的技术进步是偏向于资本的。

技术进步偏向性在中国的客观存在给我们研究技术冲击的经济波动效应提供了一个新的视角：除了技术进步水平的外生冲击，技术进步偏向程度的变动是否会对经济波动产生影响？我们阅读所及没有发现有文献对该问题进行回答，相对比较接近的是陈师和赵磊（2009）的研究，他们将投资专有技术变迁这种非中性技术变迁因素引入到一个不可分劳动RBC模型，考察这种技术变迁及其冲击对中国经济波动的影响，并将其与一个引入中性技术冲击的基本RBC模型进行了对比，发现引入投资专有技术变迁的RBC模型能够解释76%以上的中国经济波动特征，而基本RBC模型仅能解释中国经济周期波动的47%。但该研究仅仅是主观性地在RBC模型中引入了不同属性的技术进步来考察其对经济波动的影响。

为了更准确地度量技术进步的偏向程度对中国地区经济波动的影响，基于邓明（2014）估算的1990-2010年的中国省际技术进步方向的面板数据，本文构建了一个动态空间面板数据模型来实证分析技术进步的偏向程度对经济波动的影响。本文的研究结果表明，技术进步越偏向于资本，经济波动程度就越大，而技术进步速率的冲击对经济波动则没有显著影响，这说明当前技术冲击对中国地区经济波动的影响主要通过方向而非速率来起作用。此外，我们还发现，地区经济波动在时间上呈现显著的惯性特征，在经济空间上呈现出显著的空间相关性。

二、实证模型与估计技术

在这部分中，我们介绍实证分析技术进步方向与经济波动之间关系的计量模型，并说明使用的估计方法和变量。

（一）实证模型

我们所使用的基准计量模型如下所示：

其中，ins为地区在时期的经济波动程度，D为地区在时期的技术进步偏向指数，是对经济波动产生影响的变量集合，ε为随机扰动项。

托布勒（Tobler, 1970）提出的“地理学第一定律”认为任何事物都存在空间相关，距离越近的事物空间相关性越大。而不同省份之间由于地理或经济联系，使得地理距离上或是“经济距离”上相邻的地区，其经济发展存在较大的空间相关性，这一点已有大量文献证实[①]。因此，我们自然有理由认为不同省份之间的经济波动同样存在空间相关性，为此，我们在模型右边引入了被解释变量的空间自回归项。此外，考虑到经济波动可能存在的持续性特征，我们在模型的右边还引入了因变量的一阶滞后项。因此，我们在基准模型的基础上构建如下的动态面板计量模型：

其中，为空间自回归系数，用以度量地区间经济波动空间自相关性的方向和强度，w（≠）为空间权重矩阵中的第（,）个元素，用以度量地区和之间空间距离的大小，w=0。考虑到遗漏的解释变量可能存在的空间相关性，我们假定ε存在空间相关性，并满足如下设定：

，，（3）

其中，m（≠）为空间权重矩阵中的第（,）个元素，η用于测度可能存在的个体固定效应。

（二）估计技术

埃霍斯特（Elhorst, 2010）将差分GMM方法扩展到动态空间面板数据模型中，但是，其研究认为使用这种方法估计动态空间面板数据模型可能导致严重的估计偏误，尤其是对空间自回归系数的估计。而雅各布斯等人（Jacobs., 2009）则将系统GMM方法扩展到动态空间面板数据模型的估计中，发现相对于差分GMM方法，该方法能有效地减少空间滞后项系数的估计偏误，因此，本文也采用系统GMM方法来估计式（2）和（3）。首先将式（2）和（3）写成如下的矩阵形式：

第一步，对式（2）取一阶差分，以从扰动项中消除个体效应，得到：

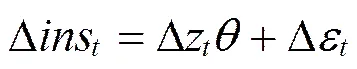
将式（4）与（5）联立得到：

（6）

为了表述方便，我们将式（6）写成如下形式：

第二步，利用SYS-GMM方法得到式（4）的参数估计量，并获得残差向量：

（8）

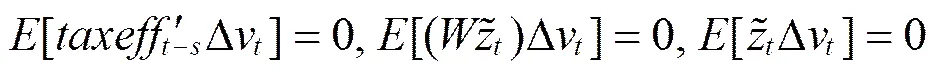
其中，=3, 4, … ,；=2, 3, … ,-1，为不包含被解释变量空间滞后项的解释变量矩阵，即。为水平方程（4）的工具变量矩阵，由如下的矩条件得到：

（10）

第三步，利用式（8）的SYS-GMM估计量，得到残差估计量，将该残差估计量代到如下由卡普尔等人（Kapoor., 2007）所提出的总体矩条件中，即可得到扰动项空间自回归系数和扰动项的方差的一致估计量：

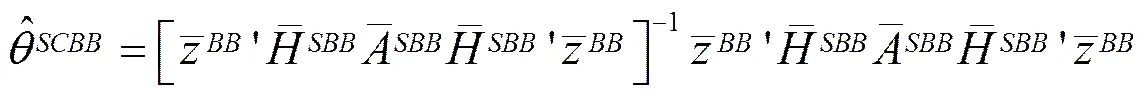
三、样本与变量

本文研究的样本是中国大陆省级地区，由于无法得到海南和重庆在较早年份的数据，且西藏的数据存在大量缺失值，因此，样本中包含了除海南和西藏以外的28各省级地区，其中重庆并入四川，样本的时间范围是1990-2010年。式（3）中的核心解释变量是各省的D。由于没有该变量的统计数据，我们使用邓明（2014）对中国省际技术进步方向指数的估计结果。邓明（2014）所构建的技术进步方向指数（D）如下所示：

其中，D是地区在时期的技术进步方向指数，E,与E,分别为地区在时期的劳动力效率与资本效率，即劳动扩张型技术进步和资本扩张型技术进步，e∈（0, +∞）为资本与劳动力的替代弹性。可以直接通过替代弹性（e）的大小以及E,/E,的变化定性判断技术进步的方向：当e<1（劳动力与资本之间是互补的）时，如果E,/E,上升（下降），则技术进步偏向劳动力（资本）；反之，当e>1（劳动力与资本之间是替代的）时，如果E,/E,上升（下降），则技术进步偏向资本（劳动力）；如果e=1，则技术进步是中性的。在最终的结果中，如果D>0，则说明技术进步是偏向资本的；如果D<0，则说明技术进步是偏向劳动力的。在估算式（13）的技术进步方向指数中，需要估算资本-劳动力替代弹性（e）以及劳动力效率（E,）和资本效率（E,），邓明（2014）采用了克伦普等人（Klump2007）的“标准化供给面系统法”（normalized supply-side system approach）对这些参数进行了估算，该方法有效地解决了劳动力-资本替代弹性的传统估算方法所存在的系统偏差问题。图1给出了不同地区技术进步方向指数的箱型图，从图中我们可以很直观地看出，仅仅从平均水平上看，大部分省份的技术进步方向是偏向于资本的；此外，东部发达省区的技术进步方向较之于中西部落后省区更偏向于资本。

图1 各省技术进步方向指数的箱型图

地区

为了考察实证分析结果的稳健性，我们采用两种方法测算经济波动（ins）：第一种方法直接利用中国各省际地区的实际GDP序列求滚动标准差来度量各地区的经济波动；第二种方法是利用趋势分离的方法将GDP序列中的长期趋势与周期性波动分离出来滞后再对分离出来的周期性波动成分求滚动标准差。在求滚动标准差的过程中，我们需要确定滚动时窗，根据现有研究，改革开放以来，我国的经济周期跨度平均为6-7年（刘树成，2009），因此我们将滚动时窗定为7年。我们使用H-P滤波法分离趋势成分。对于时序变量，H-P滤波的核心是找出使下式（14）最小化的，即为时间序列的长期趋势部分。

这里，即是各省实际GDP的自然对数。然后用原始序列减去分离出来的长期趋势部分，可得到周期性波动成分。根据拉文和尤利希（Ravn and Uhlig, 2002）的建议，我们将平滑参数取值为100。对于上述两种方法得到的经济波动，我们分别设为1和2。在控制变量集中，我们还引入了如下变量：

（1）技术冲击（）。我们用全要素生产率的增长率来度量技术进步，并采用基于产出的DEA方法计算表示生产率增长的 Malmquist指数。令和分别表示时期的投入向量和产出向量。时期的生产技术由生产可能性集合定义：={（，）：能够生产的所有}，进一步定义产出距离函数：

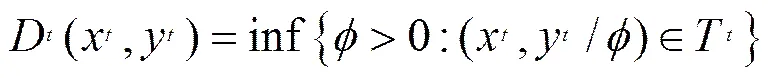
其中，inf表示集合的最大下界。距离函数的取值范围是小于等于1，即（,）≤1，而且只有当处于决定的生产可能性集的前沿边界上时才有（,）=1。借助于距离函数，我们可以进一步构造如下的Malmquist 指数：

（16）

利用DEA方法计算Malmquist指数时需要总产出、资本存量和劳动力投入三个变量的数据。我们用GDP度量总产出，并用消费者价格指数将其调整为以1990年为基期的不变价格数据，数据来自于《新中国六十年统计资料汇编》及《中国统计年鉴》；用各年度的就业人员年末人数度量劳动力投入，数据来自于《新中国六十年统计资料汇编》及《中国统计年鉴》；1990-2000年的资本存量数据使用张军等人（2004）的估算结果，并利用其方法推算了2001-2010年各省的资本存量水平，由于张军等人（2004）所计算的数据是以1952年为基期的，我们将其转换为以1990年为基期。

（2）货币冲击（）。货币主义学派认为政府的货币政策冲击是经济波动的主要来源，而货币政策变动的最直接反应是通货膨胀率的变动。因此，类似于计算经济波动的计算方法，我们用各地区的通货膨胀率7年的滚动标准差作为货币冲击变量。

（3）财政冲击（）。虽然凯恩斯理论遭到了新古典理论的批评，但我们依然无法完全忽略财政冲击对于经济波动的影响，为消除财政支出的规模差异，我们用政府一般预算支出与GDP的比重来度量财政支出水平，然后用该比率7年的滚动标准差作为财政冲击变量。

（4）金融发展水平（）。金融发展可以通过缓解流动性需求来减少经济的波动，我们用金融机构人民币各项贷款余额占GDP的比重来度量金融发展水平，其中金融机构人民币各项贷款余额的数据来自于各年度的《中国金融统计年鉴》。

（5）固定资产投资规模（）。固定资产投资在经济中扮演了重要的角色，特别是在中国，投资是政府调控经济的重要手段因而也是影响经济波动的重要因素。我们用全社会固定资产投资占GDP比重来度量固定资产投资规模。

对于空间权重矩阵的设定，我们采用如下形式：

其中，D为地区地区之间的距离，D=0（），该距离可以是传统的地理距离，也可以是地区间有关经济、制度和文化方面的广义“距离”，在本文的研究中，我们认为，首先，由于交通运输是地区间经济联系的重要工具，因此地理相邻地区的经济联系越紧密，其经济波动的相关性也越强。此外，大量研究表明，中国的地方政府在经济发展中起到了非常关键的作用，具体而言，在以经济上的高度分权与政治上的高度集权为特征的“中国式分权”背景下，地方政府形成以GDP为目标的标杆竞争（周黎安，2004），这致使经济发展水平相近地区的经济发展存在高度相关性；此外，经济发展水平相近的地区，其经济结构、阶段特征和抵御经济波动的能力也会较为接近，因此，经济发展水平相近的地区其经济波动的相关性也越强。因此，经济发展不仅存在地理距离上的空间相关性，还存在经济距离上的空间相关性。在这两个距离的度量方面，我们用省会之间的铁路里程来度量地理距离，铁路里程的数据来源于“中国火车网”中的铁路里程和票价查询系统，使用地区间最短的铁路里程数据；对于经济距离的度量，我们采用如下的方式：，其中表示地区在样本年度里的实际GDP的平均值。

上述变量如无特殊说明，数据均来自于各年度的《中国统计年鉴》和《新中国60年统计资料汇编》，[②]表1列出了上述所有变量的描述统计。

表1 变量的描述统计（1990-2009）

四、实证分析结果

（一）基准回归

首先，我们不考虑被解释变量和扰动项的空间滞后项，对式（11）的基准模型进行估计。为了克服各省之间可能存在的异方差，在这部分的回归中我们对估计参数的标准误差进行了White异方差修正。此外，我们还对使用固定效应模型还是随机效应模型进行设定检验，传统的检验方法是Hausman检验，但由于我们对估计参数的标准误差做了White异方差修正，因此，我们构造了稳健的Hausman检验。表2给出的是基准回归结果。

从表2下部的模型设定检验结果显示，面板设定的F检验均在1%的显著性水平上拒绝了模型无个体效应和时期效应的原假设，表明使用混合最小二乘回归不恰当；此外，稳健Hausman检验同样均在1%的显著性水平上拒绝了随机效应估计有效的零假设，因此我们应该使用固定效应回归，并同时控制了个体效应和时期效应。

表2 基准回归结果

注：（1）小括号内数值为回归系数的White异方差稳健标准误，中括号内数值为相应检验统计量的值；（2）***、**和*分别表示在1%、5%和10%的显著性水平下显著，下同。

从表2的基准回归结果我们可以看出，不论是以1还是2为被解释变量，也不论是否控制其他解释变量，技术进步的偏向性都会对经济波动产生显著影响，这说明了技术进步的偏向性对于经济波动作用的稳健性。当不控制其他解释变量时，技术进步偏向指数每提高1个单位，经济波动变量1会提高29.844个单位；当引入其他控制变量后，该系数变为21.325。同样，当不控制其他变量时，技术进步偏向指数每提高1个单位，经济波动变量2会提高37.023个单位；当控制其他变量时，该系数变为24.3。上述结果告诉我们，技术进步越偏向于资本，经济波动的程度越大。为何会出现这样的作用机制？我们认为，这主要是因为技术进步的偏向性对要素收入份额产生了极大影响。阿西莫格鲁（Acemoglu, 2002）从理论上证明，如果劳动与资本间是互补的（替代弹性小于1），只要资本相对于劳动增长得更快，在不考虑技术进步的情况下劳动报酬份额会上升。

与技术进步方向对经济波动的作用相对应的是，技术冲击变量（）对经济波动没有显著影响。由此可见，从短期来看，技术冲击对经济波动的影响主要通过技术进步的偏向性来实现，而技术进步速率的冲击对经济波动的作用在短期并不显著。

在其他控制变量中，财政冲击对经济波动有显著影响，财政冲击越大，经济波动越大，这一点在改变度量经济波动的方式后依然成立。此外，货币冲击对经济波动有显著的推动作用，这吻合了货币主义学派的观点，但固定资产投资并未对经济波动产生显著影响。金融发展水平能有效抑制地区经济波动，这说明在中国省际层面，并不存在金融加速器效应。

考虑到外部冲击对经济波动产生作用的时间滞后性，我们将回归模型中的外部冲击滞后一期再进行回归，我们利用与前面一样的技术手段进行了模型设定检验与参数估计，表3列出了估计结果。对于三个滞后一期的冲击变量，我们发现技术冲击的作用依然不显著，而货币冲击和财政冲击的系数估计结果和显著性水平都有所提高。说明货币冲击和财政冲击对经济波动的作用具有一定的时间滞后性，因此，在后面的分析中，对这三个冲击变量，我们均使用滞后一期的数据进行估计。

表3 基准回归结果（冲击变量滞后一期）

注：（1）小括号内数值为回归系数的White异方差稳健标准误差，中括号内数值为相应检验统计量的值。（2）变量后面的（-1）表示将变量滞后一期，下同。

（二）动态面板数据模型回归

在表4中，我们引入了税收努力程度的一阶滞后项，试图检验地方政府的税收努力程度是否存在惯性特征。我们采用系统GMM方法对模型进行估计。在估计过程中，为验证工具变量的有效性，我们对估计结果进行了Sargan检验，并对残差项是否存在一阶和二阶序列自相关进行了检验。系统GMM可分为一步法和两步法估计。相比一步法，两步法不容易受到异方差的干扰，但是在有限样本条件下，两步法的标准差可能产生向下偏倚。对此，本文利用温德梅杰（Windmeijer, 2005）的方法对两步法标准差的偏差进行矫正。

表4 动态面板数据模型的回归结果

注：小括号内数值为回归系数的White异方差稳健标准误差，下同。

表4与表3中解释变量的符号和显著性水平基本一致，说明本文结论对不同的计量回归方法是稳健的。AR（1）检验的值均小于0.1，说明残差项存在显著的一阶自相关，而AR（2）检验的值均大于0.3，说明残差项不存在二阶自相关，符合模型的设定条件；此外，Sargan检验的值均大于0.1，说明残差项与解释变量不相关，工具变量是合理的。表4中，我们重点关注的是经济波动一阶滞后项的估计结果。估计结果显示，1的一阶滞后项的估计系数为0.236，2的一阶滞后项的系数为0.341，两者均在1%的显著性水平下显著。这充分说明地区经济波动呈现出显著的持续性特征。其他变量中，除了金融发展水平估计结果的显著性水平有所降低外，其他结果与表3中的估计结果仅仅存在估计系数大小上的小幅度变动。

（三）空间动态面板数据模型回归

在表5中，我们报告了对式（2）和（3）的完整估计结果，既包含了被解释变量的时间滞后项，也包含了被解释变量的空间滞后项，并使用前文所介绍的系统GMM方法进行估计。

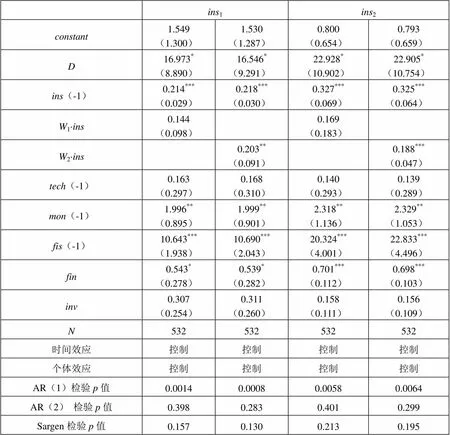
表5 空间动态面板数据模型的回归结果

注：1是以地理距离构建的空间权重矩阵，2是以经济距离构建的空间权重矩阵。

表5中模型设定检验的结果与表4中是基本一致的。将表5的回归结果与表2-4的回归结果对比可以发现，原有的解释变量的估计结果的方向和大小均未出现太大改变，只是个别解释变量的显著性程度有所改变，因此，我们的估计结果是相对稳健的。

我们所关注的是表5中新增加的被解释变量空间滞后项的估计结果，从表5中可以发现不论对于1还是2，都不存在基于地理距离的空间相关性，但均存在基于经济距离的空间相关性。具体而言，对于1，经济上相邻地区的经济波动每提高1个单位，会导致本地区的经济波动提高0.203个单位；而对于2，经济上相邻地区的经济波动每提高1个单位，会导致本地区的经济波动提高0.118个单位。事实上，出现经济空间上的波动相关性强于地理空间上的波动相关性是非常好理解的，比如广东和广西虽然地理上相邻，但其经济发展阶段存在较大差距，两者的经济波动特征必然由于经济发展阶段的不同而存在较大差异；而广东和长三角地区虽然不存在地理上的相邻性，但经济发展阶段较为接近，经济波动的关联性可能更强。因此，在对经济波动进行宏观调控时，对处于不同发展阶段的地区，我们应当根据经济发展水平进行分块调控，而不是简单地根据地理位置进行分块调控。

五、结束语

实际经济周期理论告诉我们技术冲击是导致经济波动的最重要因素，但是，我们也必须注意到，技术进步的变动不仅仅体现在速率上，还体现在技术进步的方向上，大量研究表明，技术进步不是中性的，而是带有很显著的要素偏向性，那么，技术进步的偏向性会对经济波动产生什么影响呢？为了回答这样一个问题，本文构建一个动态面板数据模型实证研究了技术进步的偏向性对经济波动的影响。

本文的研究结果表明，技术进步的偏向性显著影响了中国的地区经济波动，具体而言，技术进步越偏向于资本，经济波动程度就越大。究其原因，我们认为，技术进步的资本偏向导致了收入份额中资本份额的提高，使得资产性收入在收入来源中的比重高于工资性收入，从而导致经济波动。即使改变度量经济波动的方式，上述结论依然成立。而技术进步速率的冲击对经济波动则没有显著影响。这说明当前技术冲击对中国地区经济波动的作用主要通过技术进步的方向而非速率起作用，这是本文最重要的发现，也拓展了现有文献关于技术进步与经济波动的研究。此外，我们发现财政冲击会显著影响经济波动，但这并不能说明凯恩斯理论比新古典理论能更好地解释中国地区经济波动，主要是因为我们是基于同期的技术冲击数据与经济波动数据来考察两者之间的关系。此外，货币冲击会强化经济波动，而完善的地区金融体系则能有效地抑制地区经济波动。而且，我们还发现，地区经济波动在时间上呈现显著的惯性特征，而且在经济空间上同样呈现出显著的空间相关性，这种时空上的相关性加大了对经济波动宏观调控的难度。

本文研究为抑制经济波动提供了一个新的工具，即寻找诱使技术进步偏向于劳动力的政策工具。阿西莫格鲁（2002）认为，要素相对投入是影响技术进步偏向的重要因素。但是在当前中国老年人口抚养比不断上升、资本不断深化的背景下，为何出现技术进步的资本偏向性这样一个相悖的现象？邓明（2014）则发现，要素价格扭曲是导致中国老年人口抚养比上升背景下技术进步依然偏向于资本的一个重要因素。因此，我们建议，必须全面加快和推进要素市场的市场化改革，形成合理有效的要素价格特别是劳动力价格形成机制，这样能有利于劳动力报酬的提高，诱使技术进步偏向于劳动力，从而进一步平滑经济波动。

1. 陈师、赵磊：《中国的实际经济周期与投资专有技术变迁》[J]，《管理世界》2009年第4期。

2. 戴天仕、徐现祥：《中国的技术进步方向》[J]，《世界经济》2010年第11期。

3. 邓明：《人口年龄结构与中国省际技术进步方向》[J]，《经济研究》2014年第3期。

4. 黄赜琳：《技术冲击和劳动供给对经济波动的影响分析——基于可分劳动RBC模型的实证检验》[J]，《财经研究》2004年第6期。

5. 简泽：《技术冲击、资本积累与经济波动——对实际经济周期理论的一个检验》[J]，《统计研究》2005年第11期。

6. 林光平、龙志和、吴梅：《我国地区经济收敛的空间计量实证分析》[J]，《经济学（季刊）》2005年增刊。

7. 刘树成：《新中国经济增长60年曲线的回顾与展望——兼论新一轮经济周期》[J]，《经济学动态》2009年第10期。

8. 徐舒、左萌、姜凌：《技术扩散、内生技术转化与中国经济波动》[J]，《管理世界》2011年第3期。

9. 张军、吴桂英、张吉鹏：《中国省际物质资本存量估算：1952-2000》[J]，《经济研究》2004年第10期。

10. 周黎安：《晋升博弈中政府官员的激励与合作——兼论我国地方保护主义和重复建设问题长期存在的原因》[J]，《经济研究》2004年第6期。

11. 朱国忠、乔坤元、虞吉海：《中国各省经济增长是否收敛？》[J]，《经济学（季刊）》2013年第3期。

12. Acemoglu, D., 2002, “Directed Technical Change” [J],, 69(4), PP. 781-809.

13. Acemoglu, D., 2007, “Equilibrium Bias of Technology” [J],, 75(5), PP. 1371-1409.

14. Elhorst, J. P., 2010, “Dynamic Panels with Endogenous Interaction Effects when T is Small” [J],, 40(5), PP. 272-282.

15. Hicks, J. R., 1932, “The Theory of Wages” [M], London: Macmillan.

16. Jacobs, J. P. A. M., Ligthart, J. E. and Vrijburg, H., 2009, “Dynamic Panel Data Models Featuring Endogenous Interaction and Spatially Correlated Errors” [C], Discussion Paper 2009-92, Tilburg University, Center for Economic Research.

17. Kapoor, M., Kelejian, H. and Prucha, I., 2007, “Panel Data Models with Spatially Correlated Error Components” [J],, 140(1), PP. 97-130.

18. Kydland, F. and Prescott, E., 1982, “Time to Build and Aggregate Fluctuations” [J],, 50(6), PP. 1345-1370.

19. Klump, R., McAdam, P. and Willman, A., 2007, “Factor Substitution and Factor-Augmenting Technical Progress in the United States: A Normalized Supply-Side System Approach” [J],, 89(1), PP. 183-192.

20. Panik, M. J., 1976, “Factor Learning and Biased Factor-Efficiency Growth in the United States, 1929-1966” [J],, 17(3), PP. 733-739.

21. Ravn, M. O. and Uhlig, H., 2002, “Notes on Adjusting the Hodrick-Prescott Filter for the Frequency of Observations” [J],, 84(2), PP. 371-380.

22. Tobler, W. R., 1970, “A Computer Movie Simulating Urban Growth in the Detroit Region” [J],, 46, PP. 234-240.

23. Wilkinson, M., 1968, “Factor Supply and the Direction of Technological Change” [J],, 58(1), PP. 120-128.

24. Windmeijer, F., 2005, “A Finite Sample Correction for the Variance of Linear Efficient Two-Step GMM Estimators” [J],, 126(1), PP. 25-51.

（M）

[①]例如林光平等人（2005）、朱国忠等人（2014）的研究。

[②]本文使用的数据是1990-2010年的省际面板数据，由于计算部分变量（如经济波动、技术冲击、财政冲击）时需要用到1990年前3年以及2010年后3年的数据，而目前还没有2013年的全面统计资料，因此在后面的回归中，我们使用的是1990-2009年的中国省际面板数据。

中国博士后科学基金项目“城市间土地财政的竞争外溢与房价的空间传导”（2012M510670）、教育部人文社会科学研究一般项目“空间似无关回归模型：参数估计、设定检验及其应用”（13YJC910003）、全国统计科研计划项目“时变系数的空间面板数据模型——理论与应用”（2012LY015）。