具有脉冲和扩散项的Beddington–DeAngelis型功能反应捕食系统的持久性

蒲武军



具有脉冲和扩散项的Beddington–DeAngelis型功能反应捕食系统的持久性

蒲武军

（陇南师专数信学院，甘肃，陇南 742500）

讨论了一类具有脉冲和扩散项的Beddington–DeAngelis型功能反应捕食系统，在该系统带有齐次Neumann边界条件的情况下，借助比较定理，获得了系统有正向不变集、解的最终有界性、持久性以及捕食者灭绝的一些充分条件。

Beddington–DeAngelis型功能反应；脉冲；扩散；持久性

0 引言

在种群动力学中，时间因素和空间因素是非常重要的。因此，研究具有时滞和扩散的模型显得很有意义。近年来，运用反应扩散方程理论来研究生态领域中的捕食系统已受到了许多学者的广泛关注。在种群动力学中, 空间均匀环境中捕食系统一般可用如下常微分方程组来表示：

(1)

在系统（1）的基础上，本文考虑如下系统：

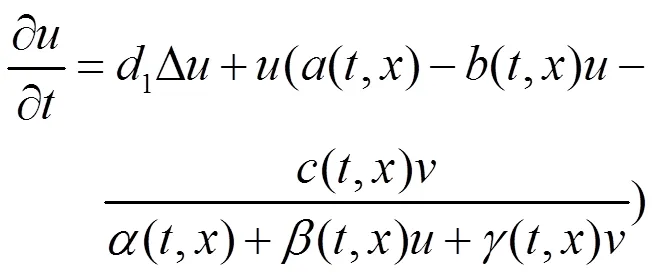
(3)

(4)

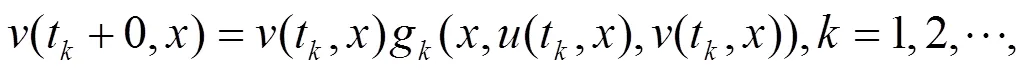
(6)

本文主要讨论系统(2)-(6)的持久性。

1 模型的基本假设和准备工作

本文始终假设：

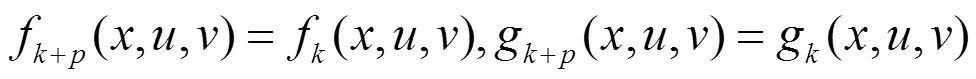
为方便期间，本文引入以下记号：

，。

2 主要结果

为证明系统(2)-(6)的持久性，先考虑如下的脉冲logistic方程：

引理2.1[4]系统（7）的每个解满足，其中。当，。

引理2.2[5]设向量值函数，满足：

，；

引理2.3[6]设,在上连续，关于连续可微，在上连续，且满足

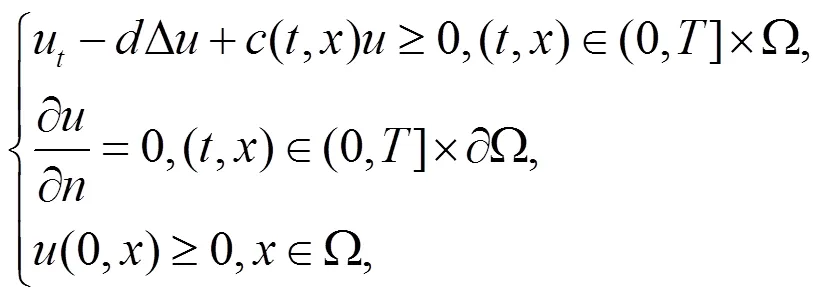
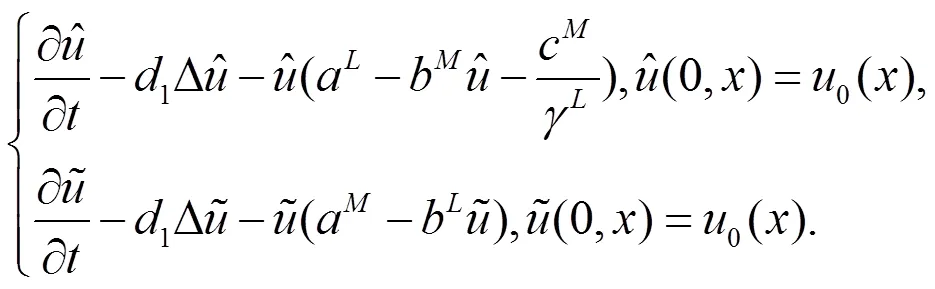
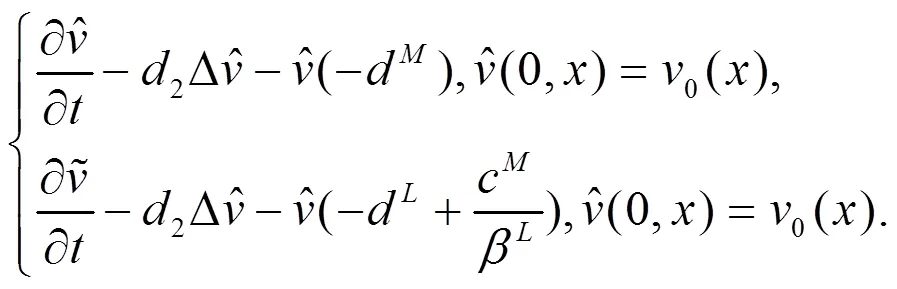
定理2.2 设条件(H1)-(H4)满足，进一步假设下面的条件成立：

得

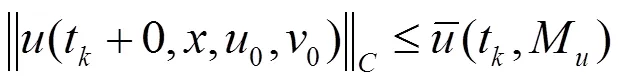
由文献[7]，知线性周期脉冲方程：

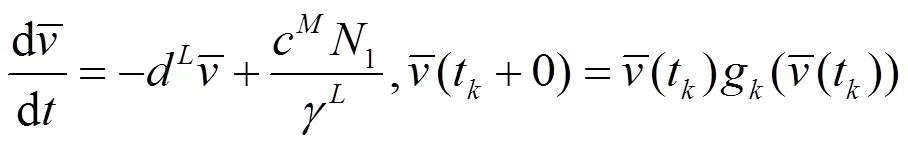
定理2.3 设条件(H1)-(H4)满足，进一步假设系统(2)-(6)满足非负初值的解是最终有界的，且下列不等式成立：

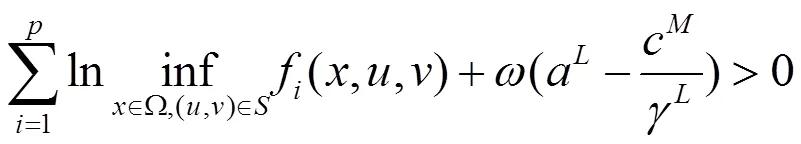
(10)

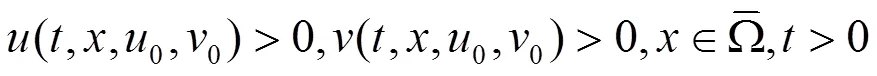
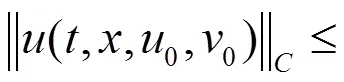
结合周期脉冲Logistic方程，

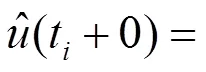
（12）

且

。

。

定理2.4 假设条件(H1)-(H4)满足，且下列不等式成立：

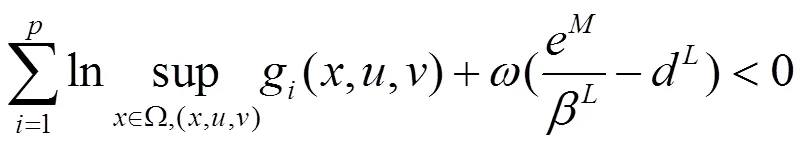
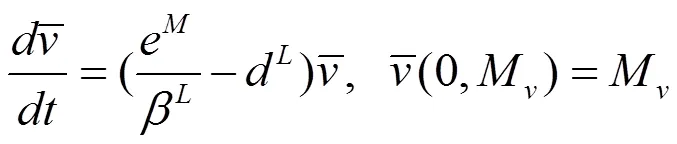
由

再次利用比较原理，可得

由脉冲条件（5）可得

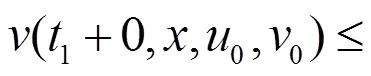
继续上述方式，可知方程（3）和（5）所对应的线性脉冲方程

参考文献：

[1] Fan M, Kuang Y. Dynamics of a nonautonomous predator–prey system with the Beddington–DeAngelis functional response[J]. Journal of Mathematical Analysis and applications, 2004,295(1):15-39.

[2] Beddington J R. Mutual interference between parasites or predators and its effect on searching efficiency[J]. The Journal of Animal Ecology,1975,44:331-340.

[3] DeAngelis D L, Goldstein R A, O'neill R V. A model for tropic interaction[J]. Ecology, 1975: 881-892.

[4] Akhmet M U, Beklioglu M, Ergenc T, et al. An impulsive ratio-dependent predator–prey system with diffusion[J]. Nonlinear Analysis: Real World Applications, 2006, 7(5): 1255-1267.

[5] Walter W. Differential inequalities and maximum principles: theory, new methods and applications[J]. Nonlinear Analysis: Theory, Methods & Applications, 1997, 30(8): 4695-4711.

[6] Smith L H. Dynamics of competition Lecture notes in mathematics[M].Berlin： Springer,1999.

[7] Samoilenko A M, Perestyuk N A. Impulsive differential equations[M].Singapore：World Scientific,1995.

[8] Liu X, Chen L. Global dynamics of the periodic logistic system with periodic impulsive perturbations[J]. Journal of mathematical analysis and applications, 2004, 289(1): 279-291.

[9] 谭德君.基于比率的三种群捕食系统的持续生存[J].生物数学学报,2003,18(1):50-56.

[10] 张正球,王志成,基于比率的三种群捕食者-食饵扩散系统的周期解[J].数学学报,2004, 47(3):531-540.

[11] 陈超,纪昆,基于比率的三种群混合扩散模型的动力学行为[J]. 纯粹数学与应用数学,2006,22(4):538-547.

[12] 史红波,具脉冲和扩散的Holling III 型捕食系统的持久性[J].兰州大学学报:自然科学版,2009,45(6):128-131.

[13] 孙树林,原存德.具有扩散和比率依赖的三种群混合模型的分析[J].系统科学与数学,2005, 25(1):87-95.

PERMANENCE OF Beddington–DeAngelis TYPE PREDATOR-PREY SYSTEM WITH IMPULSE AND DIFFUSION

PU Wu-jun

(Department of Mathematics, Longnan Teachers College, Longnan, Gansu 742500, China)

The Beddington-DeAngelis type functional response predator-prey system with impulse and diffusion under homogeneous Neumann boundary conditions were investigated. Based on the upper and lower solution method and comparison theory of differential equation, some sufficient conditions were established for the existence of positively invariant set, ultimate boundedness of solutions, permanence and the extinction of the predator in this system.

Beddington–DeAngelis functional response; impulse; diffusion; permanence

1674-8085(2015)06-0024-05

O175；Q141

A

10.3969/j.issn.1674-8085.2015.06.006

2015-05-10；修改日期：2015-06-18

蒲武军(1979-)，男，甘肃庄浪人，讲师，主要从事拓扑动力系统及应用微分方程的研究(E-mail:puwj2005@163.com).