基于p6阶第三十家族群的新LA-群

班桂宁，田 甜, 王玉琪



基于6阶第三十家族群的新LA-群

班桂宁，*田 甜, 王玉琪

（广西大学数学与信息科学学院，广西，南宁 530004）

对阶群中的进行了推广，找到了一类新的-群，并给出了这些群的一些性质，证明与验证了它们都是满足LA-猜想的LA-群。

有限-群；自由群；扩张；阶；自同构群

1 相关引理

引理1.1[9]（Van Dyek）设是由生成元和关系，所定义的群，(这些可能相同)，，，则存在唯一的满同态使得，其中为自由群，(在中的正规闭包)，。如果，则上述的为群同构(即是由生成元与定义关系，所定义的群)。

引理 1.2[1]设是有限-群，若，则正则。

引理1.3[1]设是有限群，则的全体中心内自同构组成的子群，并且它和是同构的。

引理1.4[1]设是群，且，是正整数。则有

引理1.5[1]设是群，，则

引理1.6[5]设是PN-群，和的不变型分别为和，则，其中。

2 主要结果

从而可计算出

同理可得：

(Ⅱ) 利用群扩张理论和自由群理论分3步完成定理1的证明：

如果记扩张函数:×→和:→（）有如下形状：

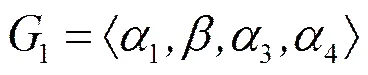
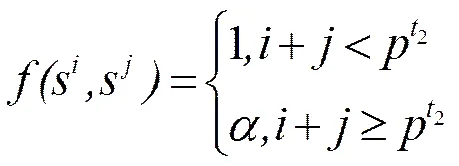
综上可得：

由此可得：

7)由文献[3]，结论显然。

定理3 由引理1.6，证明在以下情形下，

由引理1.3 有

由定理2(1)可知，

在这些情形下

[1] 徐明曜. 有限群导引（上,下）[M]. 2版.北京:科学出版社,2001.

[3] 徐尚进.有限群自同构群阶的上界[J].广西大学学报:自然科学版,1992,17(2):70-74.

[4] James R. The groups of order(an odd prime)[J]. Math. Comput,1980,34:613-637.

[5] Exarchakos T. LA-groups[J]. Journal of the Mathematical Society of Japan, 1981, 33(2): 185-190.

[6] Yu S X, Ban G N, Zhang J S. Mininal-group with automorphism groups of order[J]. Algebra Collq,1966, 3(2):97-106.

[7] Ban G N, Zhang J S ,Yu S X. The lower bound for the order of the automorphism groups[J].Proc. Roy. Irish Acad. 1996,96(2):159-167.

[8] Ban G N, Chen L Y, Zhou Y. A new series of LA-groups[J]. Journal of Guangxi Teachers Education University (Natural Science Edition),2007,24(4):5-7.

[10] 俞曙霞,班桂宁. 具有循环中心和小中心商的有限-群[J]. 广西大学学报:自然科学版, 1993,18(3):15-23.

[11] 俞曙霞,班桂宁. 关于LA-群的一个定理[J]. 广西大学学报:自然科学版,1994,19(1):1-8.

NEW LA-GROUPS BASED ON THE ORDER OF6OF THE 30th FAMILY GROUP

BAN Gui-ning,*TIAN Tian, WANG Yu-qi

(School of Mathematics and Information Sciences, Guangxi University, Nanning, Guangxi 530004, China)

We generalized the order ofofgroup and found a new series of finite-groups. Some properties of the groups are obtained and we prove them right. Finally, we proved that the groups are all new LA-groups which satisfy the LA-conjecture.

finite-group;free group;extension;order; automorphism group

1674-8085(2015)05-0014-07

O152.1

A

10.3969/j.issn.1674-8085.2015.05.003

2015-07-01；修改日期：2015-08-24

国家自然科学基金项目(61074185); 广西自然科学基金项目(0832054)

班桂宁(1962-)，男，广西南宁人，教授，硕士生导师，主要从事有限群论与控制论研究(E-mail:banguining101@sina.com);

*田 甜(1991-)，女，湖北黄冈人，硕士生，主要从事有限群论与控制论研究(E-mail:ltnco@sina.com);

王玉琪(1990-)，男，山东济南人，硕士生，主要从事有限群论与控制论研究(E-mail:944547510@qq.com)0