基于Matlab仿真的机器手臂笛卡尔轨迹规划

王涛



基于Matlab仿真的机器手臂笛卡尔轨迹规划

王涛

(江西农业大学南昌商学院, 江西南昌, 330013)

为了消除机器手臂空间轨迹规划中采用一般插补法产生尖角的问题, 结合空间直线插补和圆弧插补算法, 提出一种新的圆弧连接匀速直线插补法, 并引入“拟合度”的概念, 在Matlab环境下对算法进行了仿真。结果表明, 通过该算法以及对拟合度的调整可以获得最优规划路径。

插补算法; 笛卡尔空间; 轨迹规划; Matlab仿真

机器手臂的轨迹是指手臂的各关节在空间运动时, 随时间变化而形成位置、速度或加速度曲线。轨迹规划一般分为关节空间轨迹规划和笛卡尔空间轨迹规划。关节空间轨迹规划简单方便且不易出现特殊位形, 但是末端轨迹却存在不直观的问题。相反, 笛卡尔空间轨迹规划比较直观, 但是却常出现特殊位形, 可谓两种方法各有优缺点。目前, 学者们对关节空间的轨迹规划算法进行了大量的研究, 在较为简单的机器手臂轨迹规划中一般采用三次多项式和五次多项式插值法[1], 该类算法的优点是计算量小, 并具有连续的速度曲线, 但是却存在明显的波动。B样条曲线插值法则兼具连续速度和波动小的特点, 被更为广泛地使用, 不过B样条曲线的速度、加速度初值和终值不能同时为0。Miti等[2]通过对B样条曲线参数的优化, 获得了在约束条件下的最优规划轨迹。此外, Zhang Bin等[3]对时间进行规划, 获得满足关节速度约束条件的规划轨迹。相比之下, 对于笛卡尔空间的轨迹规划方面的研究较少, 目前被广泛使用和讨论的有空间直线插值算法和空间圆弧插值算法[4–5]等。当机器手臂的轨迹为几段连续的直线轨迹时, 会在连接处形成尖角, 从而影响轨迹的平滑性。通常的做法是将连续直线进行分离, 得到多段的独立直线, 然后对各条直线进行单独规划。这样一来就增加了轨迹的平滑性, 但电机在各段直线间会不停地启动和停止, 从而引起很大的振动和磨损[6–7]。为此, 本文在空间直线插值算法和圆弧插值算法的基础上提出了一种改进的插补算法。

1 空间匀速直线插补

空间匀速直线插补, 是指机器手臂末端从开始点沿着预定的直线轨迹匀速移动到终点的过程中, 对直线上中间点位置的确定方法[8]。设起点为0(0,0,0), 终点为1(1,1,1), 机器手臂移动的速度为, 则完成整个移动所需时间

如果令插补周期为Δ, 则插值的个数=/Δ, 同时有

(2)

其中, Δ, Δ, Δ分别为轴、轴、轴的位置增量,取整数。插值点的坐标可用式(3)表示:

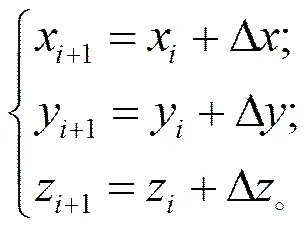
其中取整数, 取值范围为[0,]。通过式(3)可求出各插值点的位置, 然后根据逆运动学便可求出机器手臂的各个关节值, 控制关节运动, 从而使机器手臂在其末端获得直线的运动轨迹。

2 空间匀速圆弧插补

空间圆弧插补通常有4个步骤[9–10]: 第1步是根据空间中的3个点的坐标确定圆弧圆心及半径; 第2步实现空间圆弧到平面圆弧的变换, 建立坐标系; 第3步是在新的坐标系上实现圆弧插补; 第4步则是将插补后的结果映射为原坐标系的值。

设机器手臂末端从起点0经过中间点1最终到达2点。其中0(0,0,0),1(1,1,1),2(2,2,2)为空间上的3个不共线的点。则这3点可以确定一空间圆弧, 设其圆心为(,,), 则通过该空间圆弧的平面可以表示为

由3个点都在圆弧上可得

(5)

通过式(4)和式(5)可以求出圆心(,,)和圆弧半径。

以圆心为坐标原点, 建立新的坐标系, 选取→0的方向作为轴正方向, 与和组成的平面垂直的方向作为轴, 然后根据右手法则建立坐标系(图1)。

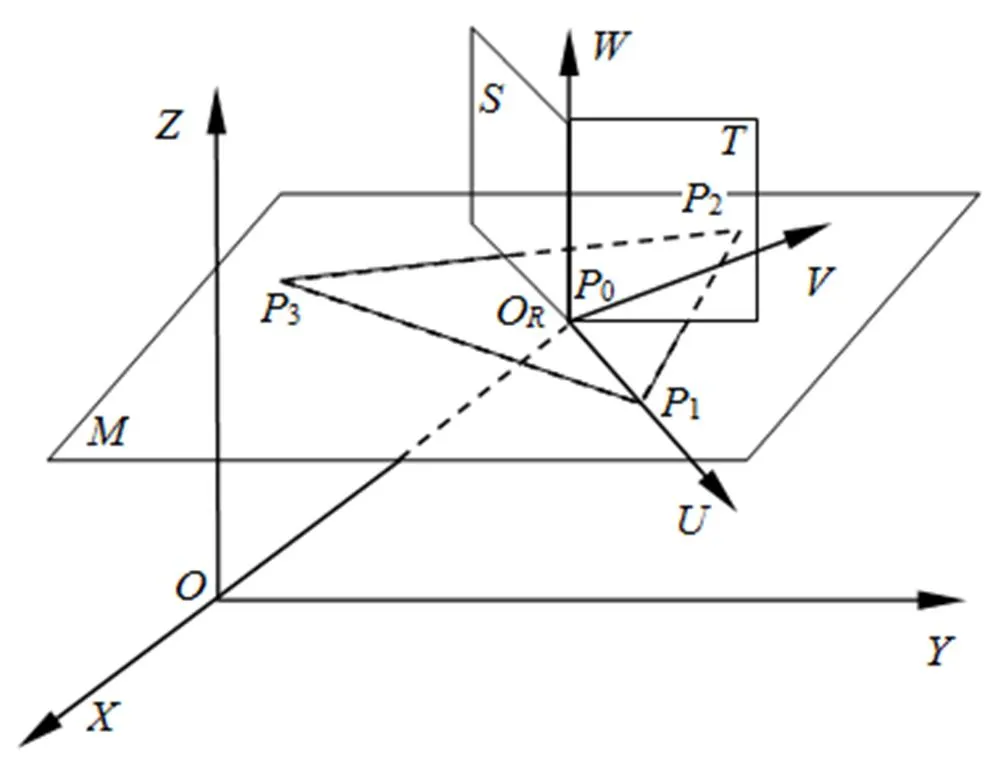
图1 XYZ–UVW坐标系图

根据上述设定, 可以求出三轴的方向向量分别为

由此可以求出原坐标系和坐标系的变换关系

。 (7)

由式(7)的变换矩阵, 可以实现坐标系和坐标系的变换,

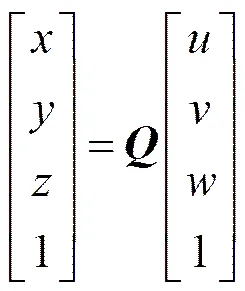
在坐标系中, 对于0,1,2和圆心, 有=== 0,0=1=2= 0,0=。

在变换后的平面内, 空间圆弧转变为了一个平面圆弧, 便可以开始坐标系下的圆弧规划了。设起点0到终点2扫过的圆弧角为, 机器手末端线速度为, 起点到终点所需时间为。令插补周期为Δ, 则插值的个数=/Δ, 第个插补点的值θ=ωΔ, 其中为角速度。则可以得出坐标下插值点, 而转换到坐标下的坐标值P(XYZ)(,,)可用式(9)求出:

3 空间圆弧连接的匀速连续直线插补

空间直线插补法和圆弧插补法是笛卡尔空间轨迹规划中最为基本的2种轨迹规划插补法。在一些简单环境工作时, 无论采用哪一种单一的插补法都能较好地实现规划任务。而当机器手臂所在的工作空间比较复杂时, 单一的插补法往往不能较好地完成任务。典型情况就是当机器手臂末端需要沿着2条直线连续运行时, 如果简单地对2条直线进行连续的直线插值, 将会使得机器手臂各关节驱动机构反复的启停动作, 从而磨损机器手臂。为此, 本文提出了一种基于空间圆弧连接的匀速空间连续直线插补法, 即通过空间的圆弧来实现对2条直线的衔接, 从而消除直线简单连接所产生的接点尖角。

空间中的2条相交的直线可以确定一个二维平面, 因此将空间中的直线转换到二维平面来分析是一个不错的选择。由图2可知, 空间上的直线1和2交于点0, 在0点处出现尖角, 为了消除其对机器手臂的不利影响, 可以选取一段同时相交于两直线的圆弧(图2)来实现两直线的连接, 交点分别为1和2。则整个机器手臂的运行轨迹为从1的起点出发经过1点, 然后通过圆弧到达交点2, 最后沿直线2到达终点。可以发现, 圆弧圆心位置的确定以及圆弧半径的大小, 将是轨迹规划的关键。

图2 直线连接图

为了使直线到圆弧的过渡更为流畅, 本文让所选定的圆弧和直线1和2同时相切, 则圆弧和1直线的切点为1, 与2直线的相切点为2。由图2可知, 由于圆弧的圆心可以自由选取, 因此内切于1和2的空间圆弧有无限多条。为了描述各圆弧相较于原始轨迹的程度, 本文定义了一个“拟合度”。被定义为圆弧连接后第1段直线轨迹长度与圆弧连接前该直线轨迹长度之比。选取不同的圆弧, 将对应不同的。因此, 其取值范围为[0, 1]。当直线与圆弧连接点与开始点重合时, 即s点为圆弧起点, 则第1段直线轨迹长度为0,取“0”值; 又有当1点选为1直线的中点时, 则为“0.5”。如果设0到1的距离为10, 直线1的长度为, 则10=× (1-)。在图2中, 由于圆弧同时相切于两直线, 因此对两直线分别作垂线, 则两垂线交点(,,)即为圆弧的圆心,1或2到点的距离则为圆弧的半径。空间圆弧连接的匀速直线插补步骤如下。

步骤1: 计算圆弧和两直线的交点坐标。设定拟合度, 根据起始点s(s,s,s)和点0(0,0,0)的三维坐标, 可计算出连接点1处的坐标,

而通过结束点e(e,e,e)和点0(0,0,0) 的三维坐标, 又可以计算出2点的坐标,

(11)

步骤2: 对s到1点之间的空间直线进行空间直线插值, 实现该段的轨迹规划。

步骤3: 计算圆弧半径及圆点。根据起点s、终点e和两直线原始交点0的坐标, 利用式(4)求出平面方程。而1和2两点在圆弧上, 因此,

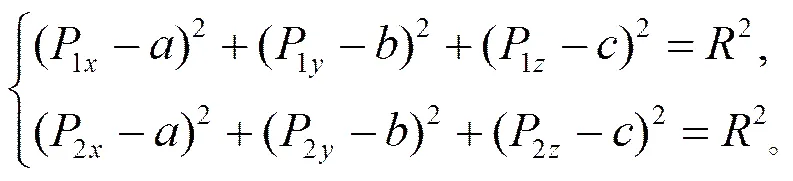
由于1和圆弧相切,的长度为圆的半径(图3), 根据勾股定理有

, (13)

其中:10为1到0的距离;d为圆心到0的距离。

根据式(4)、(12)和(13)可以求出原点()的坐标值和圆的半径。

步骤4: 构建坐标系。以圆心为坐标原点, 构建新坐标系,轴的正方向选定位→1的方向, 和、所组成的平面垂直的方向设为轴, 则可由右手法则得出轴的方向。

步骤5: 在坐标系上完成空间圆弧插补, 求出插补点P(u, v,w), 然后得出插补点在原始坐标系上的坐标值, 从而完成该圆弧段的轨迹规划。

步骤6: 对于2点到2终端的直线段, 采用空间直线均匀插值法完成轨迹规划。

通过以上6步, 可以实现空间圆弧连接的匀速连续空间直线轨迹规划。

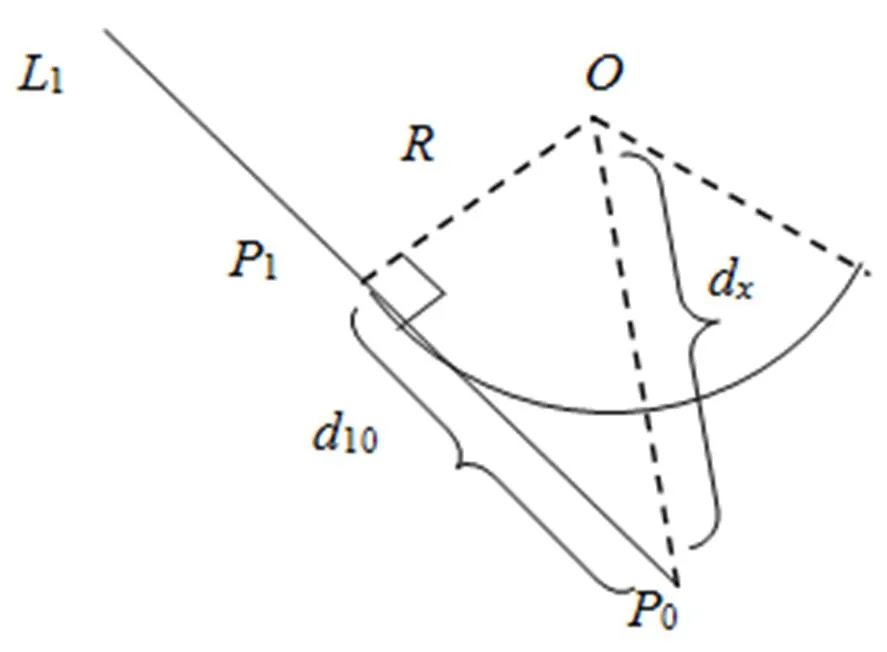
图3 圆弧和直线L1的切线

4 仿真验证

4.1 空间匀速直线插补仿真

设空间内有一条由1(200, 220, 10)和2(250, 50, 170)两点连接的直线。其中1点为机器手臂末端的起点,2为末端终点, 采用空间匀速直线插补算法绘制出笛卡尔空间轨迹规划(图4)。

仿真结果表明, 轨迹规划为直线, 满足规划要求。通过各插值点对应的坐标, 采用运动学逆解的方法可以求出机器手臂各关节需要移动的目标角度。

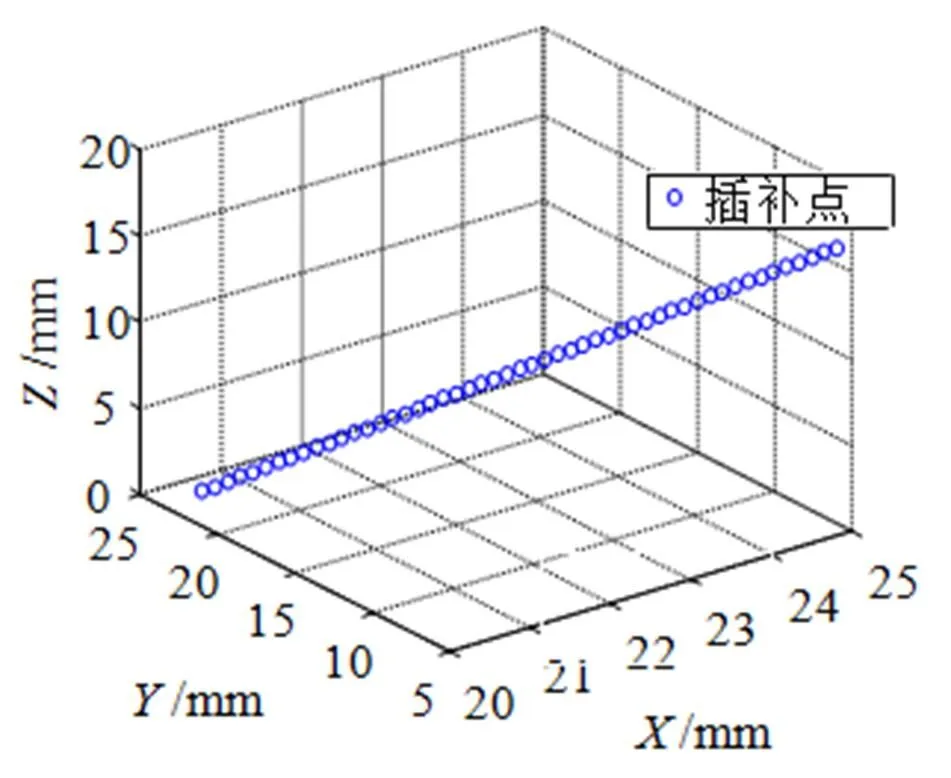
图4 空间直线轨迹规划图

4.2 空间匀速圆弧插补仿真

设空间内有不共线的任意3点1(10, 140, 130),2(150, 90, 40),3(250, 50, 70)。则3个点在空间内必定形成一个圆弧, 设1点为起点,2为中间点,3为圆弧终点。则机器手臂末端沿着该圆弧从起点运动到终点, 可以采用空间匀速圆弧插补来实现笛卡尔空间的轨迹规划(插值次数选为30), 仿真效果见图5。仿真图形显示为圆弧轨迹, 满足算法要求。

图5 空间圆弧轨迹规划图

4.3 基于空间圆弧连接的匀速连续空间直线插补法仿真

设空间内有任意3点:s(210, 120, 110),0(55, 220, 255),e(48, 28, 70), 为了使机器手臂能够平滑运行, 采用本文提出的空间圆弧连接连续空间直线插补算法, 构建一段圆弧来代替原轨迹中的尖角。首先设定一个拟合度的初值= 0.7, 然后通过Matlab软件来实现轨迹规划仿真, 仿真效果如图6(a)所示。若改变拟合度= 0.9, 可得到另一个轨迹规划仿真图6(b)。

由图6(a)可以看出, 机器手臂末端将从起点出发直线运行到1, 然后经过由1、2构成的内切于两直线的圆弧, 最后再沿直线方向到达终点。图6(a)的规划轨迹和图6(b)类似, 所不同的是2个切点的坐标发生了变化, 同时圆弧的圆心坐标也发生了变化。

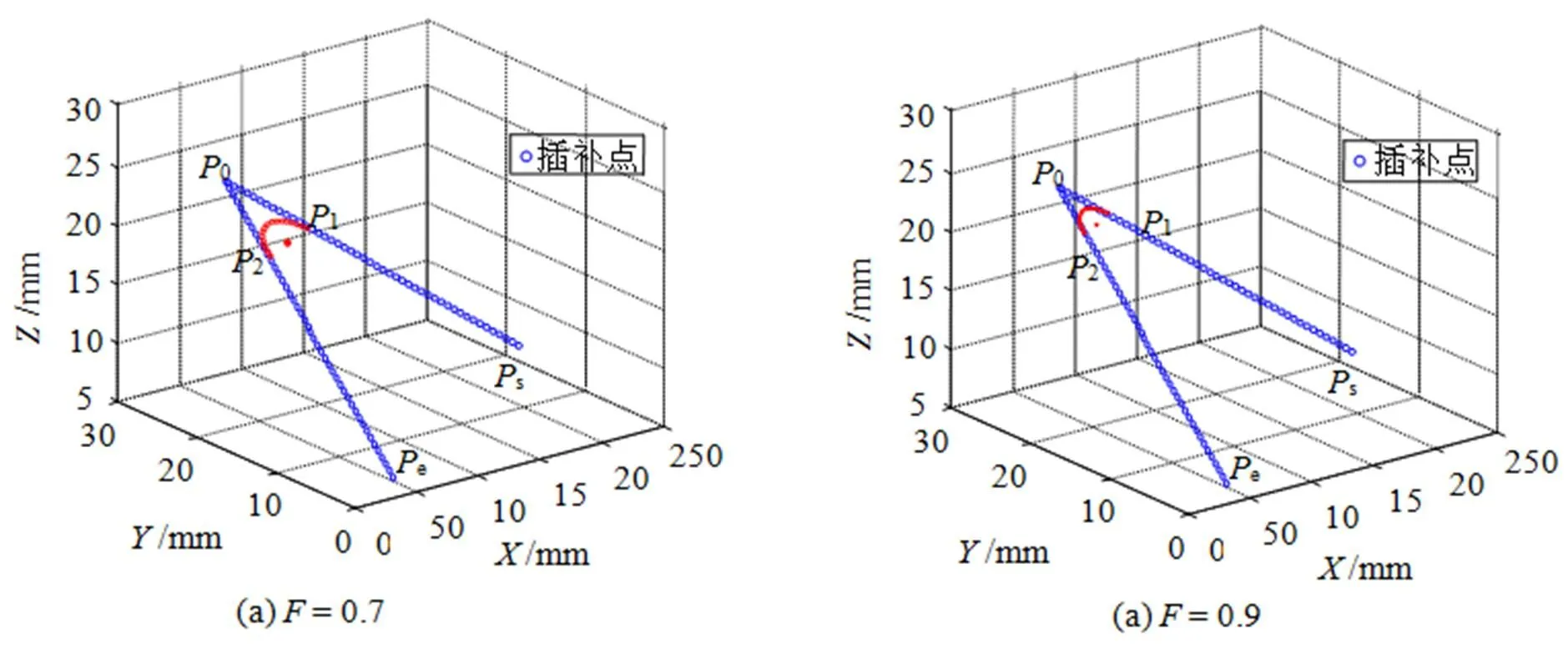
图6 基于空间圆弧连接的匀速连续空间直线插补轨迹规划图

由图6的仿真结果可以看出, 本文提出的基于空间圆弧连接的匀速连续空间直线插补轨迹规划算法符合设计要求。该算法运行稳定, 能够很好地解决连续直线中的尖角问题, 使规划轨迹变得更加平滑, 从而改善了机器手臂中各关节的磨损现象。另外, 通过选取不同的拟合度, 会形成不同的轨迹。实际规划中需要根据环境或规划要求, 选择更为适合的拟合度。一般而言, 需要高度拟合原始轨迹时, 则的取值应设置为较大值。反之, 则可以将拟合度选择得较小, 从而减少路程, 减少时间和能量消耗。

5 结论

轨迹规划对于机器手臂而言是相当重要的, 本文基于笛卡尔空间对关节型机器手臂的轨迹规划进行了分析。从空间直线插值和空间圆弧插值这2种最基本的算法着手, 针对空间连续直线出现尖角的问题, 提出了一种基于空间圆弧连接的均值连续空间直线插补算法, 并通过改变拟合度的方法实现了不同的轨迹。最后借助于Matlab软件对算法进行了仿真, 验证了本文所提出算法的稳定性, 取得了不错的效果, 具有一定的实用价值。

参考文献：

[1] 孙秀萍. 机器人手臂轨迹规划的研究[J]. 内蒙古师范大学学报(自然科学汉文版), 2009, 38(2): 174–177.

[2] Miti R, Shinichiro N. Offline and online trajectory generation with sequential physical constraints [C]// International Conference on Robotics and Biomimetics, February 21, 2009, Asian Institute of Technology, Bangkok. Washington DC: IEEE, 2008: 578–583.

[3] Zhang Bin, Fang Qiang, Ke Yinglin. Optimal time trajectory planning method for a kind of posture aligning ystem of large rigid bodies [J]. Chinese Journal of Mechanical Engineering, 2008, 44(8): 248–252.

[4] 周刚. 垂直关节型6自由度机器人笛卡尔空间轨迹规划的研究[D]. 广州: 华南理工大学, 2011.

[5] 林威, 江五讲. 工业机器人笛卡尔空间轨迹规划[J]. 机械工程与自动化, 2014, 10(5): 141–143.

[6] 林仕高. 搬运机器人笛卡尔空间轨迹规划研究[D]. 广州: 华南理工大学, 2013.

[7] 李伟光, 许阳. 搬运机器人的轨迹规划[J]. 控制与检测, 2010(5): 83–85.

[8] 陈伟华. 喷涂机器人连续直线轨迹规划的研究[J]. 机械设计与制造, 2009(8): 178–180.

[9] 衣云龙. 改进BP神经网络算法在机器人轨迹优化中的研究[J]. 沈阳工程学院学报(自然科学版), 2012, 8(01):75–78.

[10] 陈军. 多自由度机械臂实时仿真系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2012.

(责任编校:刘刚毅)

Trajectory planning of robotic arm in cartesian space based on the Matlab simulation

Wang Tao

(Nanchang Business College of Jiangxi Agricultural University, Nanchang 330013, China)

In order to eliminate the sharp corners produced in machine arm trajectory planning of general interpolation method, combined with space linear interpolation and circular interpolation algorithm, a new circular connection mean linear interpolation method is put forward. The concept of "fitting" is introduced. The algorithm is simulated in Matlab environment. The optimal planning path can obtained through the algorithm and the adjustment fitting, and the algorithm has good feasibility at the machine arm trajectory planning.

interpolation algorithm; the cartesian space; trajectory planning; Matlab simulation

10.3969/j.issn.1672–6146.2015.04.005

TP 24

1672–6146(2015)04–0020–05

王涛,husf168@gmail.com。

2015–09–21

江西省高等学校教学改革研究课题资助项目(JXJG–12–78–1)