混杂纤维钢筋自密实混凝土T-梁的抗剪承载力

尤志国，王 昊，周云龙，丁一宁

（1.华北理工大学 河北省地震工程研究中心，河北 唐山 063009；2.大连理工大学 结构工程研究所，辽宁 大连 116024）

0 引言

国内外报道了许多关于钢纤维钢筋自密实混凝土梁的抗剪性能研究成果.然而，对于混杂纤维增强的混凝土梁，国内外相关文献中没有关于合成纤维与基体粘结强度的资料，而且合成纤维与混凝土基体的粘结强度很难测出，所以不能按照钢纤维对抗剪强度贡献的方法建立经验公式.作者将纤维混凝土这种新型复合材料作为一体考虑，采用基于Rilem应力-应变法[1]和断裂力学理论的应力-裂缝口宽度法[2]计算了混杂纤维-钢筋自密实混凝土矩形梁和T-梁的抗剪承载力，并与试验值、规范计算值进行了对比.

1 抗剪承载力计算方法

1.1 RILEM应力应变法[1]

RILEM TC 162-TDF中的混凝土梁抗剪承载力的计算方法，纤维混凝土有腹筋梁的设计剪力

式中：Vcd为无腹筋梁的抗剪承载力为 钢纤维对抗剪的贡献，

1.2 RILEM应力裂缝口宽度法[2]

2 混杂纤维自密实混凝土的剩余弯拉强度和应力-裂缝口宽度关系的求解

2.1 剩余弯拉强度

材料试件梁依据RILEM TC 162-TDF[3]相关规定制作并试验.混杂纤维自密实混凝土梁的荷载-挠度曲线见图1，并计算了梁的抗弯强度及弯曲韧性，见表1.

2.2 应力-裂缝口宽度关系

根据RILEM TC 162-TDF求解裂缝口宽度和挠度的计算过程，采用matlab语言编写计算程序，求解描述应力-裂缝口宽度关系曲线的材料参数a1、a2（斜率）和2（截距）.以SF20PF0和SF20PF6为例，见图2，采用双线性的应力-裂缝口宽度曲线能够很好的预测开口梁的荷载-挠度曲线，预测得到的荷载-挠度曲线与试验采集的荷载-挠度曲线吻合良好.

表2列出反分析法得到的材料参数a1、a2和b2的值.

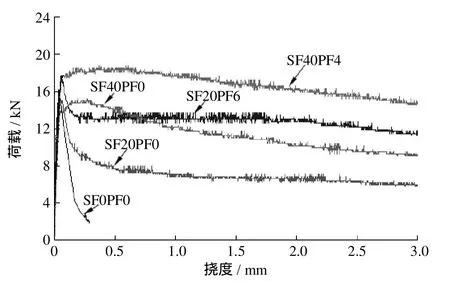
图1 混杂纤维自密实混凝土梁的荷载-挠度曲线Fig.1 Load-deflection curvesof hybrid fiber reinforced SCC beams

表1 混杂纤维自密实混凝土梁的抗弯强度及弯曲韧性Tab.1 Flexuralstrength and toughnessof hybrid fiber reinforced SCC beams

图2 SF20PF0和SF20PF6的试验荷载-挠度曲线和拟合曲线Fig.2 Load-deflection curvesof beam SF20PF0 and SF20PF6

3 混杂纤维钢筋自密实混凝土梁的抗剪承载力

3.1 试验梁参数

表2 反分析法得到的材料参数Tab.2 Materialparametersof beams based on inverse analysis

表3 梁的参数Tab.3 Parameterof beam

3.2 RILEM应力应变法

根据式 (1)和式 (2)，采用材料强度的标准值和纤维自密实混凝土的剩余弯拉强度，计算了混杂纤维-钢筋自密实混凝土矩形梁和T-梁的极限剪力，并与GB50010-2002[4]和CECS 38:2004[5]进行了对比，结果见表4．

从表4中可以看出，对于无纤维混凝土梁，采用GB50010-2002得到的预测值最接近试验值，应力-应变法次之.对于钢纤维混凝土梁，采用应力-应变法得到的预测值最接近试验值，好于CECS 38:2004.对于混杂纤维混凝土梁，采用应力-应变法能够预测梁的极限剪力，但很保守.总之，采用应力-应变法、GB50010-2002、CECS 38:2004都非常保守地（过低）估计了梁的抗剪极限承载力.

3.3 RILEM应力裂缝口宽度法

根据公式 (1)和式 (3)，计算了A系列混杂纤维-钢筋自密实混凝土梁的极限抗剪承载力，表5给出了按应力-裂缝口宽度法、应力-应变法计算的抗剪承载力的均值和变异系数.

由表5可见，对于无腹筋梁，应力-裂缝口宽度法的均值和变异系数均好于应力-应变法.采用应力-裂缝口宽度法能够较好地预测梁的抗剪极限承载力，好于GB50010-2002、CECS38:2004、应力-应变法.对于有腹筋梁，应力-裂缝口宽度法的均值好于应力-应变法.

3.4 考虑翼缘对抗剪的贡献

对于有腹筋梁或有纤维的梁，T-梁翼缘部分对抗剪的贡献不能忽略.参照文献 [8]，定义T-梁的等效有效宽度计算T-梁抗剪强度时，用有效宽度替代腹板宽度即可

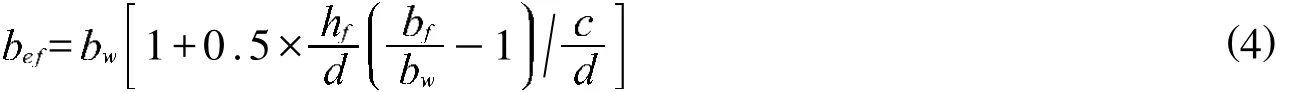
式中： 按下式计算，取正根

根据式 (4)，并采用应力-裂缝口宽度法计算了 T-梁的抗剪极限承载力，表6计算了按应力-裂缝口宽度法、应力-应变法计算的T-梁的抗剪承载力的均值和变异系数.

由表6可见，对于无腹筋 T-梁，采用应力-裂缝口宽度法计算的抗剪承载力的均值（1.04）和变异系数（0.17）均好于其它方法.对于有腹筋 T-梁，采用应力-裂缝口宽度法计算的抗剪承载力的均值（1.32）好于应力-应变法，但变异系数略大（0.18）.因此，采用应力-裂缝口宽度法很好的估计了 T-梁的抗剪极限承载力，而且应力-裂缝口宽度法可以预测混杂纤维混凝土梁的抗剪极限承载力，而其它方法只适用于钢纤维混凝土梁.

表4 梁的极限剪力Tab.4 Ultimate shear load of beams

表5 纤维-钢筋自密实混凝土矩形梁的均值和变异系数Tab.5 Mean and Coefficientof Variation of fiber reinforced SCC beams

表6 纤维-钢筋自密实混凝土T-梁的均值和变异系数Tab.6 Mean and Coefficientof Variation of fiber reinforced SCC T-beams

4 结论

采用应力-应变法和基于断裂力学理论的应力-裂缝口宽度法计算了混杂纤维-钢筋自密实混凝土矩形梁和T-梁的抗剪极限承载力，并与GB50010-2002、CECS 38:2004进行了对比，结果表明：采用应力-应变法非常保守地（过低）估计了矩形梁和T-梁的抗剪极限承载力.考虑T-梁翼缘对抗剪的贡献，采用基于断裂力学理论的应力-裂缝口宽度法能很好地估计纤维自密实混凝土无箍筋矩形和 T-梁的抗剪极限承载力；较保守估计纤维自密实混凝土有箍筋矩形梁和T-梁的抗剪承载力.

[1]RILEM TC 162-TDF，Test and design methods for steel fiber reinforced concrete--design method，final recommendation[S].Materials and Structures，2003，36：560-567.

[2]RILEM TC 162-TDF，Testand designmethods for steel fibre reinforced concrete，Design of steel fibre reinforced concrete using the -w method:principlesand applications[S].Materialsand Structures，2002，35：262-278.

[3]RILEM TC 162-TDF.Test and design methods for steel fiber reinforced concrete，BENDING TEST [J].Materials and Structures，2002，35（253）：579-582.

[4]GB50010-2010，混凝土结构设计规范 [S].北京：中国建筑工业出版社，2011.

[5]CECS 38:2004，纤维混凝土结构技术规程 [S].北京：中国建筑工业出版社，2004.

[6]Casanova P，RossiP.Analysisand design of steel fiber reinforced concretebeams[J].ACIStructural Journal，1997，94（5）：595-602.

[7]CasanovaPascal，RossiPierre，Schaller Isabelle.Cansteel fibers replace transverse reinforcementsin reinforced concretebeams[J].ACIMaterials Journal，1997，94（5）：341-353.

[8]Loannis P Zararis，Maria K Karaveziroglou，Prodromos D Zararis.Shear strength of reinforced concrete T-beams[J].ACIStructural Journal，2006，103（5）：693-670.