球面阵列基线测向算法的误差分析

司伟建，赵嫔姣，刘鲁涛



球面阵列基线测向算法的误差分析

司伟建，赵嫔姣，刘鲁涛

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨，150001)

针对传统立体基线测向算法中阵元摆放形式单一和天线盘体积受限等问题，提出球面阵列基线测向算法。首先根据简单的几何理论推导出辐射信号入射到不同基线得到的相位差公式，然后采用记忆梯度法求解3个相位差公式构成的非线性方程，得到辐射信号的来波方向。最后通过推导与化简基于球坐标下天线阵列的测向误差公式，从理论上证明球面3根天线阵列被一平面截得的圆为球大圆时测向误差最小，进而提出天线阵列的最佳摆放形式。研究结果表明：与同类算法相比，该算法中阵元位置由平面扩展到空间，摆放更加灵活，使得多模制导的导引头中基线空间位置关系不受限制；所提算法的测向性能(测向均方误差和解模糊概率)良好，对通道不一致系统具有较强的鲁棒性。

球面阵列基线法；测向性能；记忆梯度法

反辐射导弹(anti-radar missile, ARM)主要以防空系统中的无线电辐射源为目标，重点打击、摧毁防空系统雷达[1]。在现代战争中多采用多模制导技术，在天线盘体积受限的情况下天线可能无法共面排列，因此，要求天线阵列具有更加灵活的摆放形式。被动测向[2]目前主要有2类方法：空间谱估计法[3]和干涉仪测向法[4]。空间谱估计算法中比较典型的算法有波束形成(capon beam forming, CBF)[5]法、Capon最小方差(minimum variance method, MVM)[6]法、经典MUSIC(multiple signal classification method)算法[7]、ESPRIT(estimation of signal parameters via rotational invariance techniques)算法[8]、加权子空间拟合法(weighted subspace fitting ,WSF)[9]等。与空间谱估计法相比，干涉仪测向法具有实时性好、运算量小、灵敏度高等优点，但相位干涉仪测向方法在基线长度大于辐射信号波长的一半时会产生相位模糊。狄慧等[10]提出的基于联合到达时间估计的长基线测向算法具有较强的解模糊能力，但是系统复杂度较高。刘满超等[11]提出四元T形阵列干涉仪测向解模糊方法，该算法通过计算聚类中心实现解模糊，但测向精度不高。在非均匀圆阵天线模型[12]中，天线间距不受宽频带测向中高频段信号波长的限制[13]，故其测向精度高，但该算法使得多模制导的导引头中基线空间位置关系被约束在1个平面内，故在实际应用中难以实现。为此，本文作者提出一种球面阵列基线测向算法，实现阵元摆放形式从二维的平面阵列到三维的空间阵列的转变，从而使阵元摆放形式更加灵活，使得多模制导的导引头中基线空间位置关系不受限制。

1 测向原理

空间笛卡尔坐标系测向系统如图1所示，其中轴垂直向上，轴水平向右，轴代表天线视轴方向。射线为入射信号，将在空间直角坐标系内进行投影：在平面内投影与轴的夹角定义为方位角，记为；与面的夹角定义为仰角，记为；在平面内的投影与轴夹角定义为航向角，记为；在平面内投影与轴夹角定义为俯仰角，记为。这4个角具有如下关系：

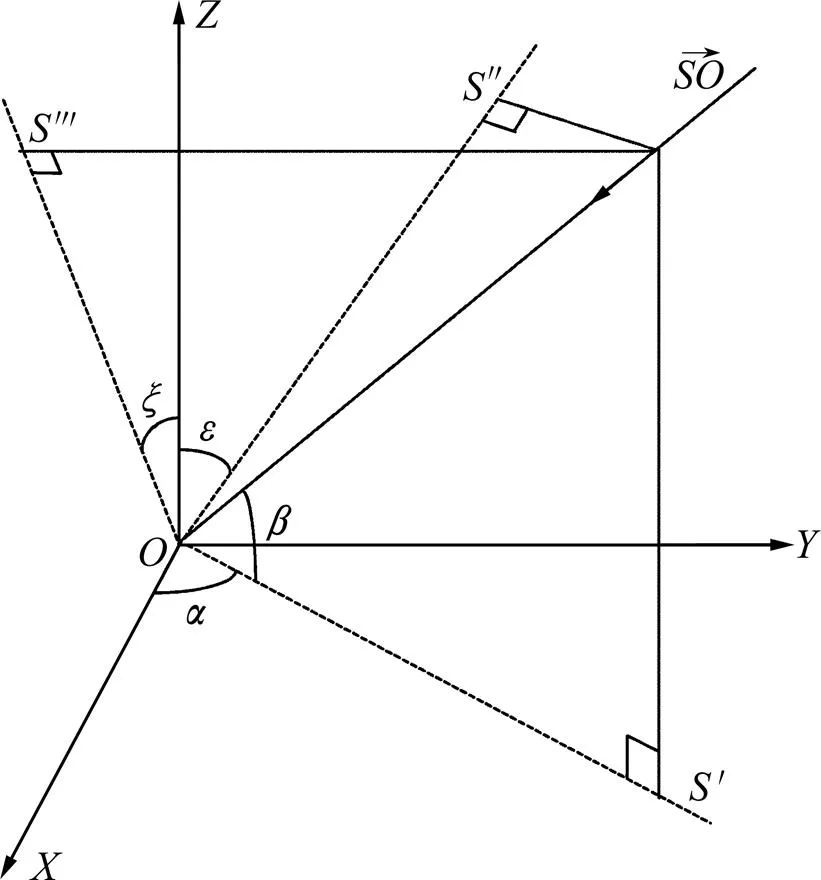
图1 入射信号模型

任意基线空间分布如图2所示，3根天线阵元位于空间笛卡尔坐标系中，空间位置坐标为(x,y,z) (=1, 2, 3)，入射信号的载波波长记为。假设不存在相位的多值模糊问题，根据简单的几何关系推导出辐射信号入射到天线1，2和3得到不同的相位差：

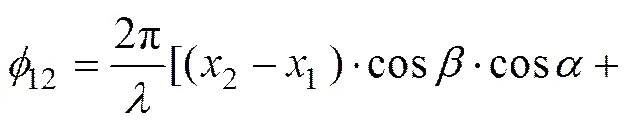
(3)

(4)

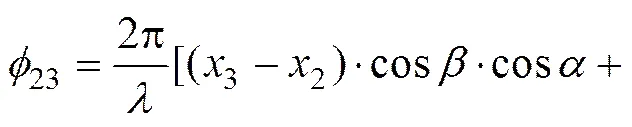
(5)

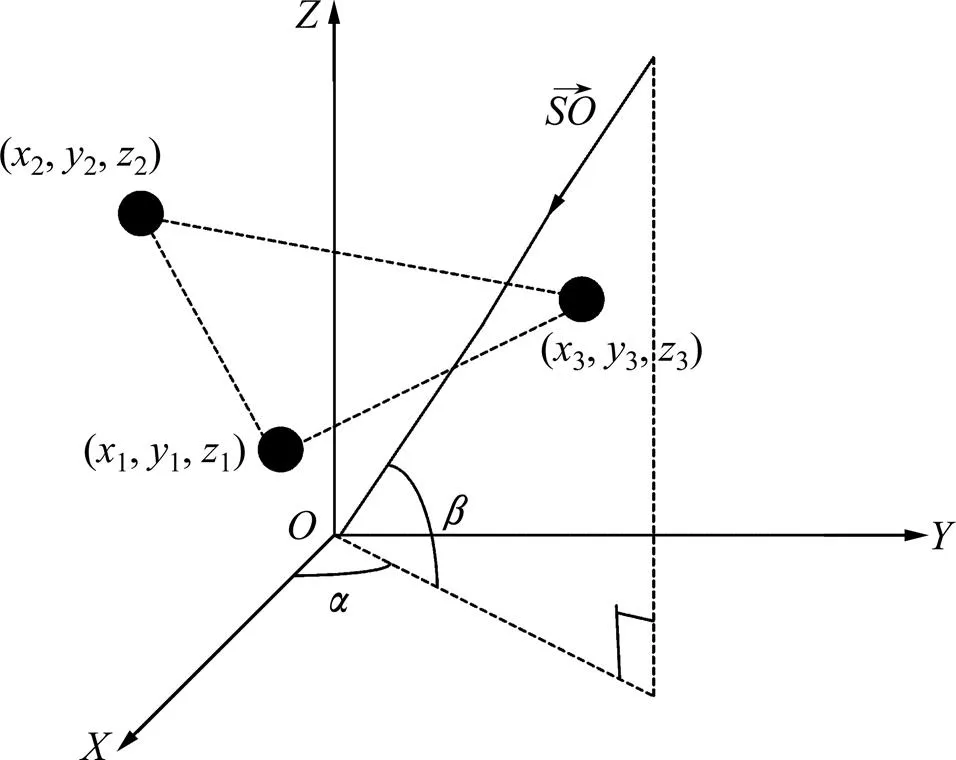
图2 任意基线空间分布

(6)

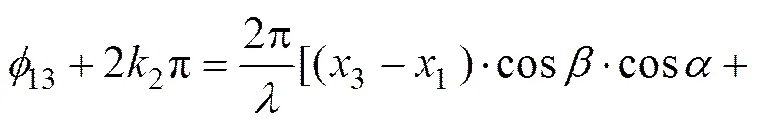
(7)

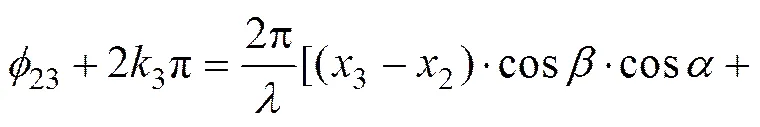
(8)

其中：k(=1, 2, 3)为任意整数。由于式(6)~(8)中任意一式可由另外2式的线性组合来表示，即三者是相关的，故通过3式中任意2式联立的方法无法求解出和的数值解。因此，本文采用记忆梯度法[14]对关于和的非线性方程组进行求解。将式(6)和(7)联立构造新的函数，有

2 球面阵列测向误差推导

3根天线分布在球表面的任意位置，如图3所示。在对测向误差进行理论推导时，假设天线基线长度小于半波长。分别对式(6)和式(7)两边变量和求偏导数后联立求解可得：

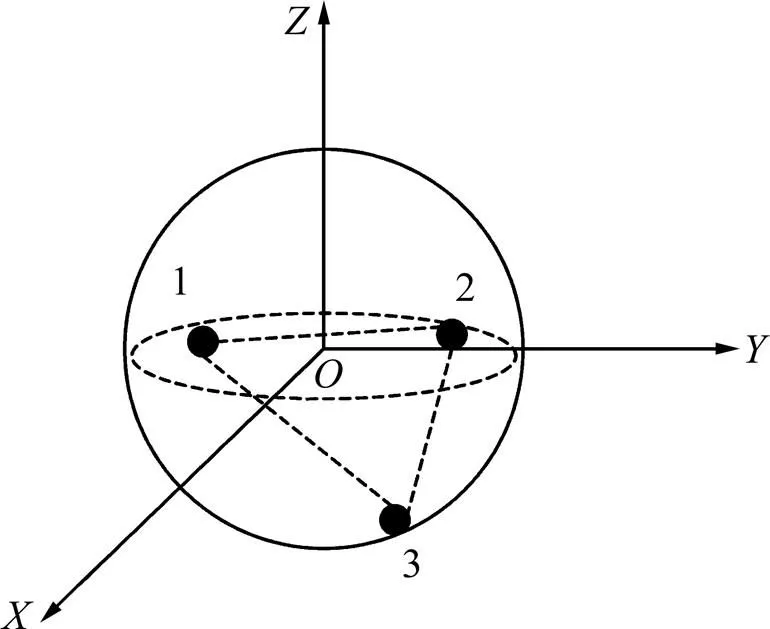
图3 球面基线空间分布

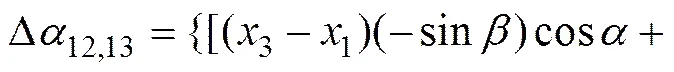
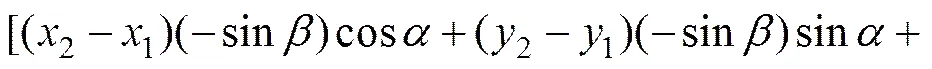
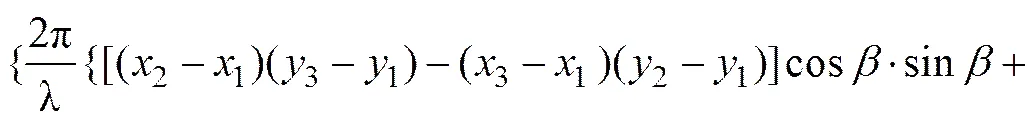
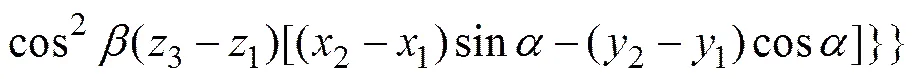
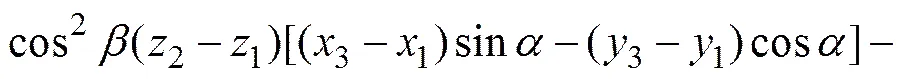
(15)

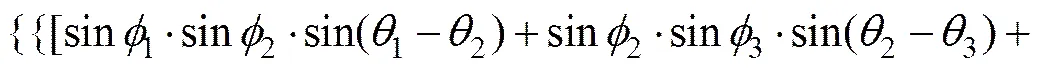
(16)

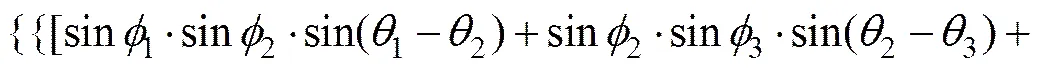
(17)

由文献[15]可得：同一平面内3根天线摆放成等边三角形阵列时测向误差最小。本文以此作为前提，研究空间位置不同的3根天线构成的等边阵列的测向性能。球面上3根天线构成的平面对球体的截面为圆，依据截面圆的大小将截面圆分成2类：球大圆和球小圆。其中，截面圆周长最大的圆为球大圆，其余为球小圆，如图4所示。图中只有，和3根天线所在平面为球大圆平面，其余全为球小圆平面。由于对下半球面阵元的研究与上半球面的原理相同，这里以上半球面为例研究空间位置对测向性能的影响。

假设在轴与上半球表面的交点处固定1根天线，记为天线1，满足90°，0°。同时，在上半球表面上以轴为对称轴取2个对称点，在这2个对称点处摆放2根天线，分别记作天线2和天线3，满足，；，。其中：和均表示区间范围内任意一个角度，且满足(0°, 90°)，(0°, 180°)。将，，，，和代入式(16)和(17)，经过化简得

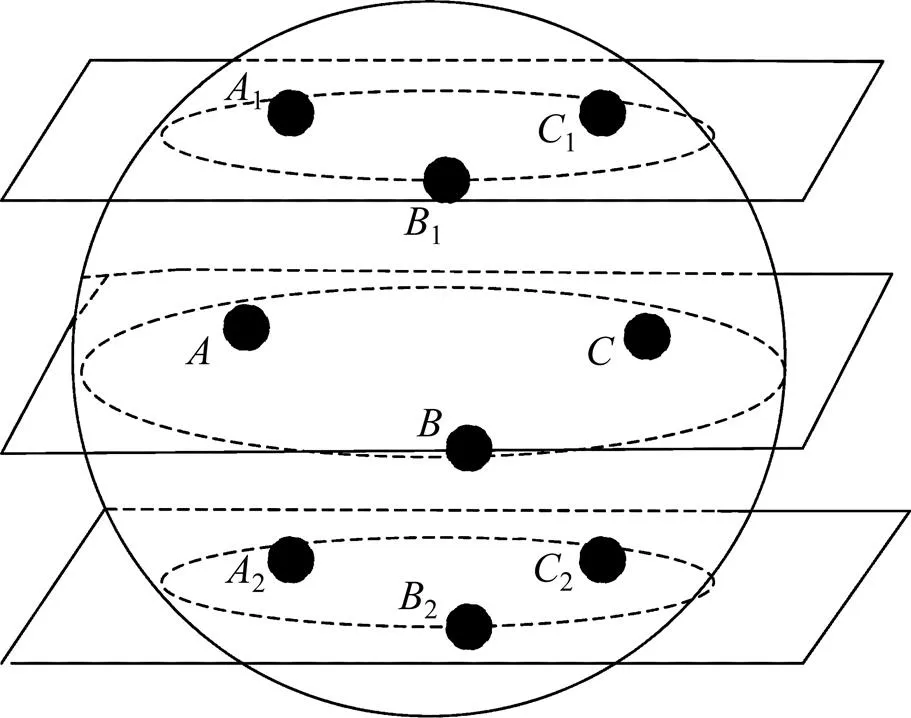
图4 球大圆平面和球小圆平面

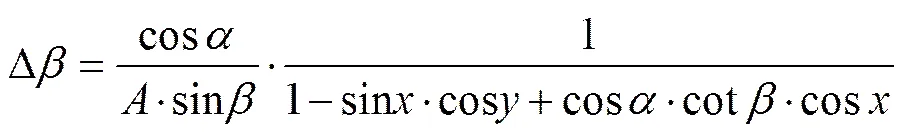
将式(21)进行三角变换，根据，和三者之间的关系可得

式(23)成立需满足条件：

解得

将式(23)进行三角变换，得

假设天线2在右半球面，天线2与原点连线在面投影与轴的夹角的取值范围为(0°, 180°)。

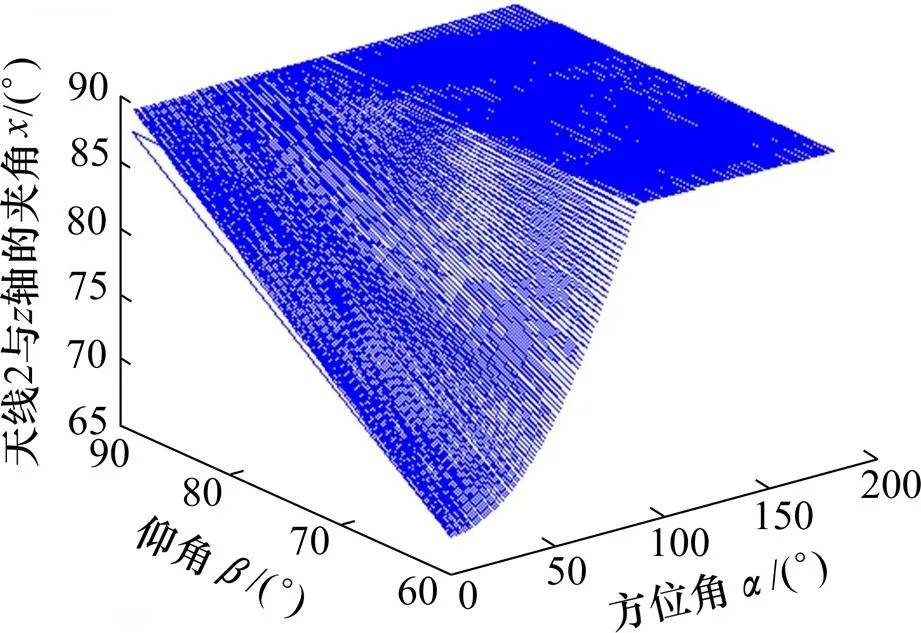
图5 天线方位角、仰角与空间位置关系

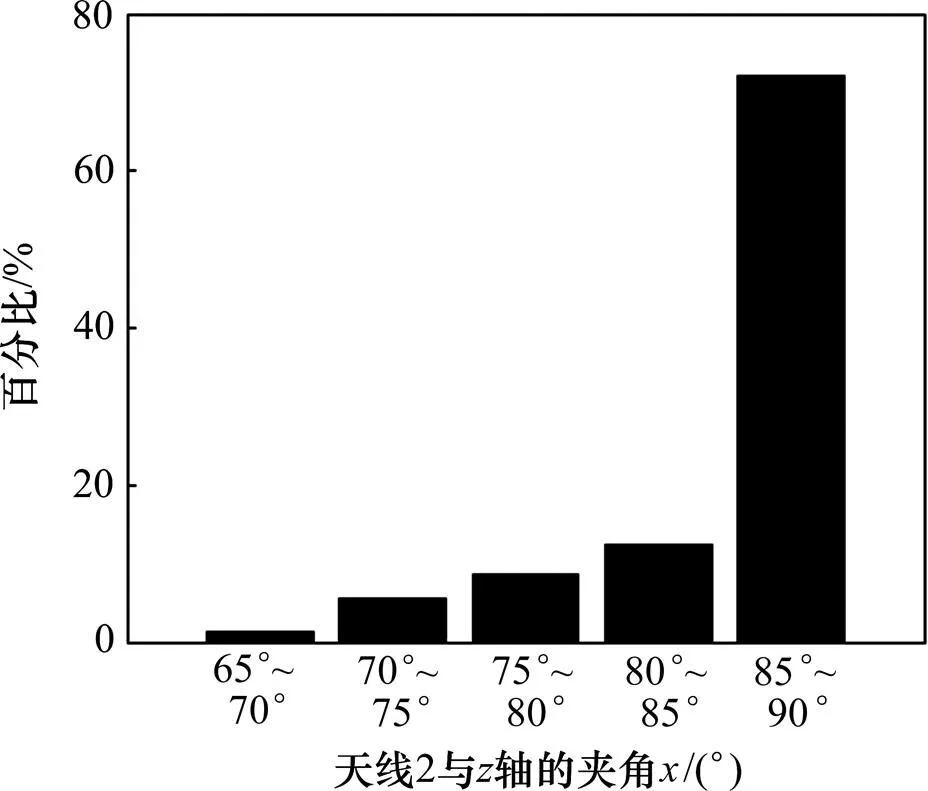
图6 图5中夹角x统计柱状图

由图5和图6可知：天线2和原点的连线与轴的夹角取85°~90°时，天线阵列对接近80%的来波方向进行测向时，可使测向误差最小。此时，天线2和3接近赤道面(用平面沿水平方向截1个球体，得到的最大圆所在平面称为赤道面)，该3根天线阵列所在平面构成近似球大圆。为此，提出球面阵列基线测向算法中使得测向误差最小的天线最佳摆放位置，该最佳摆放位置为：沿球面分布3根天线阵列摆放成球大圆等边阵列。

3 五元天线阵列的仿真模型

在实际测向中，天线间距可能大于辐射信号半波长，用由三元天线构成的一组天线阵列进行测向会得到包含模糊多值的解，因此，三元天线阵列无法完成精确测向。若用多元天线构成的多组天线进行测向，则每组天线都会得到一组测向值且各个测向值之间相差较大，真实值即为一定误差范围内各组天线共有的测向值，因此，采用多组天线进行测向可以解决测向模糊问题。但天线数目增加使得各天线间不一致性增加，因此，在实际中，大多采用五元天线阵列进行测向。五元天线阵列测向原理与三元天线阵列的测向原理相同，相当于同时进行两组三元天线阵列测向。从5个阵元中选取1个作为公共阵元，其余4个阵元平均分成2组，2组阵元分别与公共阵元组合按照前面介绍的原理重复进行2次三元天线阵列测向。其中3根天线摆放成球大圆等边三角形阵列以保证测向精度，另外2根天线与公共天线组合以解决测向模糊问题，从而实现精确测向。

在仿真过程中，取阵元所在球的半径=100 mm，根据前面的结论球面五元天线阵列中选取3根天线阵列摆放成球大圆等边三角形，另外2根天线阵列在公共天线两侧对称摆放。五元天线阵列的坐标分别为：1)；2)；3)； 4)；5)。这平面五元阵列的各天线坐标见文献[16]。在下面实验中，解模糊概率是指进行100次Monte-Carlo测向统计，将实际测出的角度与理论值进行对比得到测向误差，若100次测向中有68次误差小于设定门限值0.5°[17]，则认为计算解模糊成功，将解模糊成功次数与测向总次数相比得到解模糊概率。DOA估计结果中航向角和俯仰角的联合均方误差计算式为

实验1 取频率=12 GHz，快拍数=30，信噪比SN=12 dB。由于本文算法针对不相关信号进行波达方向估计，故选取4组不相关信号(方位角和仰角的点对)入射到阵列，分别为(80°, 24°)，(85°, 120°)，(78°, 258°)和(87°, 298°)。图7所示为本文算法进行100次Monte-Carlo试验的估计结果。

图7 4组不相关信号的方位角和仰角的估计结果

从图7可以看出：本文所提算法可以较精确地估计不相关信号的来波方向。估计结果中存在个别估计值与其他试验结果误差较大，但估计结果整体集中，各次试验的误差均在±2°之内，验证了本文所提算法的有效性。

实验2对比本文提出的球面阵列的立体基线测向算法与文献[16]中的测向算法的测向性能。仿真条件如下：频率8 GHz，方位角=60°，仰角=80°，相位差平均次数=100，信噪比分别为3，6，8和12 dB。2种算法的DOA估计的测向均方误差和解模糊概率随信噪比SN的变化分别如图8和图9所示。

由图8和图9可知：在相同信噪比条件下，本文所提算法的均方误差整体小于文献[16]中算法的均方误差，两者之间的差值在信噪比较低的情况下较明显，随着信噪比的增加两者的差值逐渐减小；在相同的信噪比下，本文所提算法的解模糊概率大于文献[16]中算法的解模糊概率。由于在求解来波方向时，本文算法采用记忆梯度法进行多次迭代，故测向精度更高。取信噪比SN分别为3，6，8和12 dB。当信噪比为 3 dB时，本文所提算法的最大均方误差为0.48°，最小解模糊概率为0.9，解模糊概率随着信噪比的增加而单调递增，最终在信噪比SN≥8 dB时解模糊概率 为1。

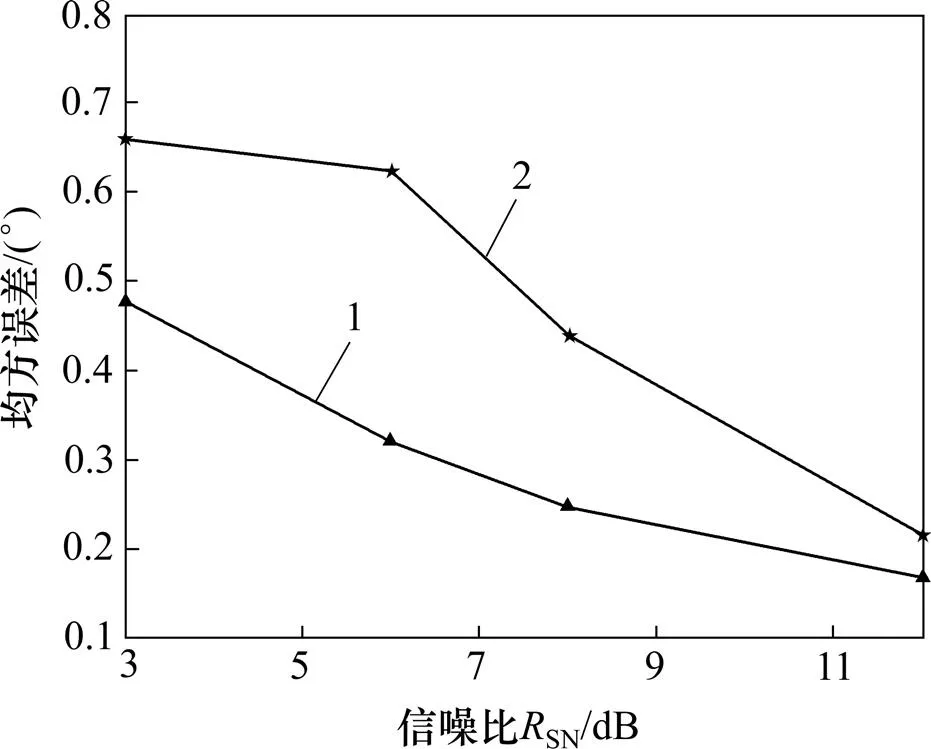
1—本文算法；2—文献[16]中算法

1—本文算法；2—文献[16]中算法

实验3系统存在通道不一致时本文算法与文献[16]中算法的测向性能分析。试验中，天线系统存在3°和10°的通道不一致(即在天线通道间人为加入的附加相位差最大值为3°和10°)，信噪比SN=12 dB，相位差平均次数分别取10，30，50，100和200次时，2种算法的DOA估计测向均方误差随相位差平均次数的变化如图10所示，2种算法的DOA估计解模糊概率随相位差平均次数的变化如图11所示。

从图10可以看出：当天线系统通道不一致(在实际测向系统中由于环境温度、湿度、器件、加工工艺等因素所致)和相位差平均次数相同时，本文算法的测向均方误差小于文献[16]中算法的测向均方误差。当相位差平均次数相同时，随着天线系统存在的通道不一致性增加，测向均方误差呈增大趋势；当天线系统存在的通道不一致性相同时，测向均方误差随相位差平均次数的增加而减小。图11中，对比本文算法和文献[16]中算法的解模糊概率随信噪比的变化曲线可以看到：解模糊概率与天线系统存在的通道不一致程度成反比，与相位差平均次数成正比。综上可以看出：当系统存在通道不一致时，本文所提算法测向性能要优于文献[16]中算法测向性能，即本文算法对系统通道不一致有较强的鲁棒性。

1—10°通道不一致，本文算法；2—10°通道不一致，文献[16]中算法；3—3°通道不一致，本文算法；4—3°通道不一致，文献[16]中算法

1—10°通道不一致，本文算法；2—10°通道不一致，文献[16]中算法；3—3°通道不一致，本文算法；4—3°通道不一致，文献[16]中算法

4 结论

1) 针对多模制导的导引头中由于空间位置受限导致基线难以共面的问题，提出了基于球面阵列的立体基线测向算法，该算法中阵元空间位置摆放灵活，使得基线的空间位置关系不受限制。

2) 该算法采用记忆梯度法求解相位差方程组，与其他求解非线性方程组的方法相比，记忆梯度法无需求解雅克比矩阵的逆矩阵，计算量较小。

3) 通过对球面3根天线阵元模型测向误差公式的数学推导，从理论上证明了球面3根天线阵列摆放成球大圆时测向误差最小这一结论，进而给出了立体基线测向算法中3根天线球面阵列的最佳摆放位置。

4) 由于实际测向中存在测向模糊，根据前面3根天线阵元模型的测向原理对5根天线阵元模型测向算法进行仿真与分析，验证了本文所提算法的有效性，且本文测向算法测向性能优于平面基线算法测向性能，本文算法对系统通道不一致有较强的鲁棒性。

[1] 吕科. 防空导弹武器系统与反辐射导弹的对抗研究[J]. 航天电子对抗, 2006, 22(4): 1−3. LÜ Ke. Countermeasures of air defense missile system against anti-radar missile[J]. Aerospace Electronic Warfare, 2006, 22(4): 1−3.

[2] ZHOU Rongguo, ZHANG Hualiang, XIN Hao. Improved two-antenna direction finding inspired by human ears[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(7): 2691−2697.

[3] ZHENG Jimeng, Kaveh M. Sparse spatial spectral estimation: A covariance fitting algorithm, performance and regularization[J]. IEEE Transactions on Signal Processing, 2013, 61(11): 2767−2777.

[4] Kebeli M. Extended symmetrical aperture direction finding using correlative interferometer method[C]// 2011 7th International Conference on Electrical and Electronics Engineering, ELECO. Bursa, 2011: II-209− II-213.

[5] Stoica P, WANG Zhizhong, LI Jian. Robust capon beamforming[C]// 2002 36th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 2002: 876−880.

[6] Capon J. High-resolution frequency-wave number spectrum analysis[J]. Proceedings of IEEE, 1969, 57(8): 1408−1418.

[7] Kaveh M, Barabell A J. The statistical performance of the MUSIC and the minimum-norm algorithms in resolving plane waves[J]. IEEE Transactions Acoustics, Speech, Signal Processing, 1986, 34(2): 331−341.

[8] Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions Acoustics, Speech, Signal Processing, 1989, 37(7): 984−995.

[9] Jansson M, Swindlehurst A L, Ottersten B. Weighted subspace fitting for general array error models[J]. IEEE Transactions on Signal Processing, 1998, 46(9): 2484−2498.

[10] 狄慧, 刘渝, 杨健, 等. 联合到达时间估计的长基线测向相位解模糊算法研究[J]. 电子学报, 2013, 41(3): 496−500. DI Hui, LIU Yu, YANG Jian, et al. Long baseline direction finding unwrapping phase ambiguity algorithm with TOA estimation[J]. Acta Electronica Sinica, 2013, 41(3): 496−500.

[11] 刘满超, 杨建红. 四元T形干涉仪测向解模糊方法研究[J]. 信息通信, 2013(2): 31−33. LIU Manchao, YANG Jianhong. Study on the methods of solving direction finding ambiguity in T-array with four antenna[J]. Information & Comunication, 2013(2): 31−33.

[12] 张春杰, 李智东. 非均匀圆阵天线模型解模糊误差研究[J]. 系统工程与电子技术, 2012, 34(8): 1525−1529. ZHANG Chunjie, LI Zhidong. Research on solving ambiguity error of nonuniform circular antenna array model[J]. Systems Engineering and Electronics, 2012, 34(8): 1525−1529.

[13] 毛虎, 杨建波, 刘鹏. 干涉仪测向技术现状与发展研究[J]. 电子信息对抗技术, 2010, 25(6): 1−6. MAO Hu, YANG Jianbo, LIU Peng. The actuality and development of phase interferometer technology[J]. Electronic Warfare Technology, 2010, 25(6): 1−6.

[14] 汤京永, 董丽.一类新的求解非线性方程组的记忆梯度法[J]. 信阳师范学院学报(自然科学版), 2011, 24(3): 311−312. TANG Jingyong, DONG Li. A new memory gradient method for solving nonlinear equations[J]. Journal of Xinyang Normal University (Nature Science Edition), 2011, 24(3): 311−312.

[15] 司伟建, 万良田. 立体基线算法的测向误差研究[J]. 弹箭与制导学报, 2012, 32(4): 13−17. SI Weijian, WAN Liangtian. The research on direction-finding with spatial baseline[J]. Rockets, Missiles and Guidance, 2012, 32(4): 13−17.

[16] 司伟建, 初萍, 孙圣和. 基于半圆阵的解模糊技术研究[J]. 系统工程与电子技术, 2008, 30(11): 2128−2131. SI Weijian, CHU Ping, SUNG Shenghe. Research on solving ambiguity technology based on semi-circle array[J]. Systems Engineering and Electronics, 2008, 30(11): 2128−2131.

[17] GU Jie. Wavelet threshold de-noising of power quality signals[C]// 2009 5th International Conference on Natural Computation, ICNC. Tianjin, China, 2009: 591−597.

(编辑 陈灿华)

Direction finding error of spatial baseline algorithm based on spherical array

SI Weijian, ZHAO Pinjiao, LIU Lutao

(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)

To deal with the scenario that the placement form of antennas is single and the placement space of antennas is finite, which is common in traditional spatial baseline algorithm, a novel algorithm based on spherical array was proposed. Firstly, the phase difference expressions of incident signal impinging on the different antennas were deduced on the basis of simple geometric theory. Then, nonlinear equations consisting of three phase-error formulas were solved by taking advantages of the memory gradient method, and the direction of arrival (DOA) of the incident signal was obtained. Finally, through derivation and simplification of error formulas of azimuth angle and elevation angle in the spherical coordinates, it was proved that when three antenna arrays were placed in the biggest circle, the direction-finding error was the miminum, thus the best format of antenna arrays in the proposed algorithm could be given. Compared with other similar existing algorithms, the arrays in the proposed algorithm could be placed in three-dimensional space instead of two-dimensional plane, which eliminates the limitation that baselines must be coplanar in the seeker of multimode guidance. The simulation results demonstrate the effectiveness and better direction-finding performance of the proposed algorithm when considering the root mean square error and solving ambiguity probability. Moreover, the proposed algorithm is robust to channel inconsistency.

spherical array baseline algorithm; direction-finding performance; memory gradient method

10.11817/j.issn.1672-7207.2015.09.022

TN911

A

1672−7207(2015)09−3317−08

2014−09−12；

2014−11−29

国家自然科学基金资助项目(61201410)；中央高校基本科研业务费资助项目(HEUCF130804) (Project(61201410) supported by the National Natural Science Foundation of China; Project(HEUCF130804) supported by the Fundamental Research Funds for the Central University)

司伟建，博士，研究员，从事宽带信号处理、检测与识别及高分辨高精度测向技术研究；E-mail: swj0418@263.net