面接触齿轮传动原理及几何设计方法

宋洪舟，魏世民，廖启征，郭磊



面接触齿轮传动原理及几何设计方法

宋洪舟，魏世民，廖启征，郭磊

(北京邮电大学自动化学院，北京，100876)

为增大齿轮齿面间接触区域，减小接触应力，提出一种基于面接触的齿轮传动形式。根据平面连杆机构中高副低代原理，在齿面之间添加滑动块、改变齿廓形状，使齿面间点、线接触转变为面接触；利用复数矢量法建立内外啮合传动的运动学模型，得到传动比、角速度、角加速度方程；研究滑动块几何参数和理想条件下的尺寸约束方程，分析齿廓与滑动块之间的相对位置，得出主动齿轮、从动齿轮齿数选择的临界条件，讨论不通过情况下的齿数选择范围。利用三维造型工具对面接触齿轮传动进行结构设计并仿真分析。研究结果表明：面接触齿轮传动仿真结果与理论预测结果一致，为其进一步推广和应用提供了依据。

齿轮；面接触；啮合；滑动块；高副低代

齿轮是机械传动中应用最广泛的部件，目前齿轮传动形式按齿面之间的接触特点可以分为点接触和线接触[1−2]，像渐开线齿轮、摆线齿轮其啮合瞬时的接触状态为直线，而大多数齿轮传动主要以点接触为主，即使是理论上为线接触的齿轮，在安装误差等因数影响下，也会转变为点接触[3]。从运动副角度来看，点、线接触均属于高副接触[4]，高副接触的缺点在于单位面积承受应力大，考虑到材料变形与齿之间作用力的影响下，接触点、线会拓展成为椭圆区域，从一定程度上减小了接触应力[5]。国外学者主要针对配对齿面的综合曲率半径、齿面修型以及接触椭圆的运动特点等方面进行了研究[6−9]；国内学者利用有限元法对齿轮进行接触分析[10−12]。齿轮传动与连杆机构有着密不可分的联系，齿轮传动是连杆机构的拓展和延伸[13]。在进行运动学分析时，通常利用平面机构中的高副低代原理[14−15]，将齿轮高副接触瞬时替代为铰链四杆机构。本文作者进一步利用高副低代原理，在保持原有自由度基础上，通过在2个齿轮之间添加构件的方法，将点、线接触转变为曲面之间的低副接触，减小齿面间接触应力，最终形成一个脉动输出运动的传动形式，这种类型的传动适用于低速、重载对传动精度要求不高的场合。

1 共轭齿廓的形成原理

1.1 齿轮传动的瞬心与齿廓曲率中心位置

图1所示为1对共轭齿廓瞬时啮合位置。从图1可见：在1对相互啮合的齿轮中，1和2是2个齿轮的回转中心，齿轮齿廓分别为和，且在点处切触，直线′是通过接触点两齿廓的公法线，从图1中可以看到两齿廓曲率中心1和2，虚线表示曲率圆，曲率半径为和。

齿轮作为构件可以用1和2来标记，机架用构件0来表示。根据瞬心定义，齿轮相对机架的瞬心就在转动副中心处，记为01和02；两齿廓接触点处的运动副类型为平面高副，齿轮1相对齿轮2的瞬心在过接触点公法线方向。

根据三心定理，2个齿轮的相对瞬心12应在直线0102与′的交点处，容易得到2个齿轮瞬时传动 比为

在啮合某一瞬时，齿廓接触点处的相对运动速度为矢量12，根据齿廓啮合基本定理，切点的相对运动速度必定在公切线方向，数学表达式为

1.2 齿轮传动中的高副低代原理

对于含有高副的平面机构进行研究分析时，可以将机构中的高副根据一定条件虚拟地以低副替代，这种方法称为高副低代[4]。进行替代时必须满足以下2个条件：

图1 1对共轭齿廓瞬时啮合位置

1) 替代前后机构的自由度相同。

2) 替代前后机构的瞬时速度和瞬时加速度相同。

在平面齿轮机构中，齿廓之间的接触形式为点接触或线接触，从运动副角度来看，这2种接触形式均为高副接触，主动、从动齿轮分别绕各自回转中心做定轴转动，那么在某一瞬时可以采用高副低代原理进行研究。在瞬时啮合点处，可用杆件12连接2个齿廓曲线和的曲率中心1和2，曲率中心分别与各自回转中心1和2连接，这样组成了铰链四杆机构1122(图2)。接触点处的高副由中间杆件两端低副1和2代替，中间连杆12作为新添加的第3个构件，瞬时替代铰链四杆机构的自由度、瞬时速度、瞬时加速度均与替代前齿轮传动机构保持不变。

1.3 面接触齿轮传动形成原理

为改变齿轮副之间的接触形式，可以考虑把齿廓之间的点、线接触转变为曲面与曲面接触。图2所示为齿轮传动等效铰链四杆机构。以图2所示的铰链四杆机构为原型，同样利用高副低代原理，将中间杆件12替换为两侧呈凹面的滑动块。图3所示为增加滑动块的瞬时替代机构。从图3可见：相应2个齿廓取凸圆弧齿廓和，其圆心在原齿廓曲率中心处，滑块两侧曲面与凸圆弧齿廓等半径且始终贴合，滑块两侧中点用1和2来标记。

忽略与原齿轮传动的瞬时速度、加速度对比，保持机构自由度数目不变，使凸圆弧齿廓作为主动轮，顺时针转动1个微小角度，齿廓推动滑动块运动，滑动块挤压从动齿廓逆时针转动，滑动块作为1个传递运动的活动构件，始终与两侧齿廓曲面贴合并且相对滑动，得到下一时刻运动状态图，如图4 所示。

图2 齿轮传动等效铰链四杆机构

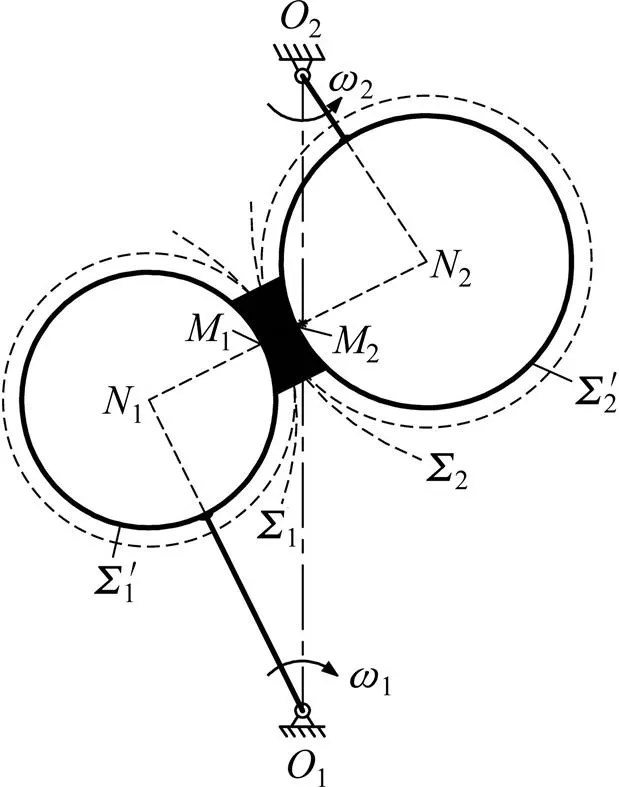
图3 增加滑动块的瞬时替代机构

上述1对齿在啮合过程中，最大特点是凸圆弧齿廓与中间活动滑块实现了曲面与曲面之间的滑动接触，齿廓单位面积压力减小，但输出传动比不再是定值，但通过优化结构尺寸能够减少传动比波动情况。

为使这种以面接触为特点的齿轮传动机构连续不间断传递运动，将圆形齿廓分别绕其回转中心圆周布置若干齿数，滑动块和其中1个齿轮齿数相同，通过复位元件使滑块贴合齿面且与齿轮径向呈一定初始角度。主动齿轮连续推动从动齿轮上的齿运动，这样形成了面齿轮传动形式。图5所示为面接触齿轮传动啮合原理图。

图4 替代机构的下一时刻姿态

(a) 外啮合传动；(b) 内啮合传动

2 面接触齿轮传动的运动学模型

用复数矢量表示为

对式(5)实部虚部分离：

对式(4)进行求导得

3 啮合特点分析

即当后面1对齿进入啮合时，必然会因为速度差而产生碰撞会导致前1对齿的脱离，在实际啮合过程中仅有1对齿处在工作状态，而且为保证面接触齿轮正常工作，从动轮齿廓必须始终在主动轮齿廓的同 一侧。

4 滑动块的几何参数与约束条件

4.1 滑动块几何参数

滑动块是实现面接触传动的重要媒介，滑动块的各项几何参数均影响传动比变化规律，为研究方便起见，定义滑动块的基本几何参数如图7所示。

图7 滑动块几何参数

滑动块的两侧曲面均为圆弧形，分别与相接触的凸圆弧齿廓曲率半径相同，最薄处厚度记为；滑动块宽度方向与中间端面对称，宽度为；滑动块两侧边缘形成的中心角分别为和，有以下关系：

4.2 尺寸约束条件

面接触齿轮的各项基本尺寸必须在一定取值范围之内，根据12与主、从动轮径向是否共线，可以得到理想条件下尺寸之间的约束关系。

满足三角形法则：

保持主动轮始终沿一个方向推动从动轮转动，而不发生反转情况：

式中：“+”适用于外啮合；“−”适用于内啮合。

5 内、外啮合的齿数选择

5.1 齿数选择范围的临界条件

对于面接触齿轮传动而言，当1个圆形齿廓和滑块能够刚好能够进入2齿之间时，是区别与分度圆内侧齿廓还是外侧齿廓啮合的临界条件，以下按照不同场合来讨论。

(a) 从动轮临界啮合位置；(b) 主动轮临界啮合位置

式中：“+”适用于外啮合；“−”适用于内啮合。

5.2 齿轮的最少齿数

实际传动中，2齿轮的齿数不能太少，必须保证2对齿在铰链四杆机构对应“死点”位置之间，否则传动就会产生中断。因此，可以得到最少齿数为

5.3 齿轮的最多齿数

齿轮齿数越多，越容易发生干涉现象，所以，要根据临界条件分别讨论主动轮、从动轮最多齿数。现以外啮合传动为例，内啮合与此类似过程。

6 齿根过渡与仿真分析

面接触齿轮传动的齿面接触应力变小，但为了提高齿根弯曲强度，相邻凸圆弧齿之间采用圆弧过渡。图9所示为齿轮安装细节。滑动块的中心角影响齿根危险截面的宽度，通过计算得知：在相同外形尺寸和齿数的条件下，采用较小的滑动块，面接触齿轮的齿根弯曲强度高于渐开线齿轮的齿根弯曲强度。

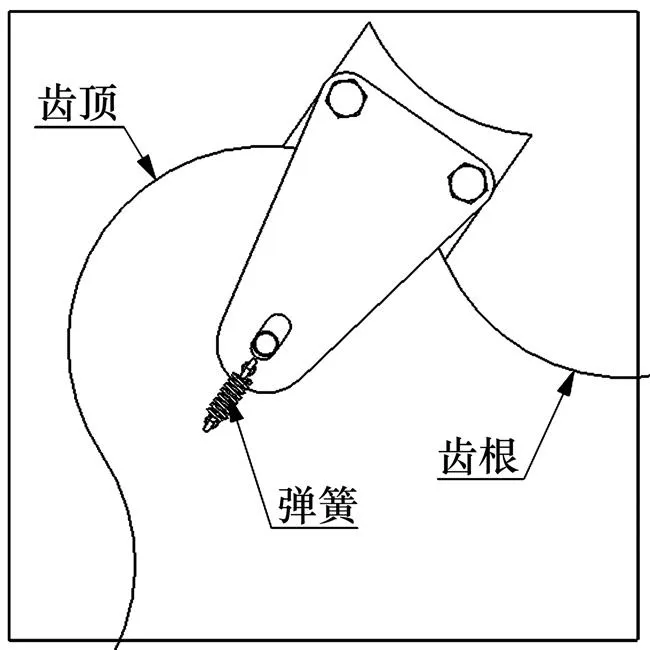
图9 齿轮安装细节

现给定以下1组基本结构参数：齿轮中心距= 100 mm；齿轮1分度圆半径1=50 mm；齿轮2分度圆半径2=50 mm；齿轮1齿廓曲率半径3=8 mm；齿轮2齿廓曲率半径4=8 mm；滑块中心厚度=2 mm；滑块的宽度=6 mm。利用齿数判断条件，初选齿轮1齿数1=8；齿轮2齿数2=8，对齿轮各元件装配并进行运动仿真。

根据式(13)可以得到传动比曲线如图10所示。从图10可见：虚线段为极限位置之间的理想传动比曲线；实线段为实际啮合过程中，1对齿的传动比变化范围；进入、脱离啮合1次过程中的平均传动比为；实际传动比变化的极差。计算结果表明：当中心距存在误差时，平均传动比的值变化很小，说明面接触齿轮传动对中心距误差不敏感，有利于实际应用。

面接触齿轮传动适用于低速重载的场合，仿真时假设主动齿轮进行慢速转动，转速为1=10 r/min。图11所示为从动轮仿真转速曲线。从图11可见：通过仿真软件得到从动轮的角度速度在62 rad/s附近，并且呈现周期性波动变化，变化趋势与理论计算相近，验证了传动可行性。

图10 传动比曲线

图11 从动轮仿真转速曲线

7 结论

1) 以增大齿轮齿面间接触面积为目标，考虑降低齿面间的运动副类型，利用平面连杆机构中的高副低代原理，在齿与齿间添加滑动块，并且改变相互啮合齿廓形状，最终形成1种面接触齿轮传动机构。

2) 建立了面接触齿轮传动的运动学模型，说明该机构的传动比为变量，当齿轮连续传动时，输出的运动为脉动形式。

3) 面接触齿轮传动齿数受到中心距、分度圆半径、滑动块等方面参数的限制，在推荐数值范围内，配对齿数有多种组合选择。

4) 滑动块作为实现面接触的中间媒介，可安装主动齿轮或从动齿轮，但须由弹性元件保证滑动块的初始位置，并起到复位作用。

5) 齿根采用圆弧过渡，其弯曲强度比一般渐开线齿轮的高。面接触齿轮传动适合低速重载场景，能够预见，以此原理研制成的减速器可用于千斤顶或船舶起抛，因此，从工程实际角度来看，该传动类型具有一定的应用价值，若要进一步推广，还需进行深入 研究。

[1] 朱孝录. 齿轮传动设计手册[M]. 北京: 化学工业出版社, 2010: 343−346. ZHU Xiaolu. Handbook of gear design[M]. Beijing: Chemical Industry Press, 2010: 343−346.

[2] 王丽娟, 黄清世, 邹雯. 齿轮发展研究综述[J]. 机械研究与应用, 2008, 21(1): 17−18. WANG Lijuan, HUANG Qingshi, ZOU Wen. Research on the summarization of the gear development[J]. Mechanical Research & Application, 2008, 21(1): 17−18.

[3] Litvin F L. Gear geometry and applied theory[M]. Cambridge: Cambridge University Press, 1994: 1−50.

[4] 孙桓, 陈作模, 葛文杰. 机械原理[M]. 北京: 高等教育出版社, 2007: 5−8. SUN Huan, CHEN Zuomo, GE Wenjie. Theory of machines and mechanisms[M]. Beijing: Higher Education Press, 2007: 5−8.

[5] 徐顺. 基于分形理论的齿轮接触模型的研究[D]. 合肥: 合肥工业大学机械与汽车工程学院, 2008: 15−26. XU Shun. Study on the gear face contact model based on the fractal theory[D]. Hefei: Hefei University of Technology. School of Machinery and Automobile Engineering, 2008: 15−26.

[6] CHEN Ningxin. Curvatures and sliding ratios of conjugate surfaces[J]. Transactions of the ASME, 1998, 120(3): 126−132.

[7] CHEN Ningxin. Edges of regression and limit normal point of conjugate surfaces[J]. Transactions of the ASME, 2000, 122(4): 419−425.

[8] Feng P H, Litvin F L. Determination of principal curvatures and contact ellipse for profile crowned helical gears[J]. Transactions of the ASME, 1999, 121(1): 107−111.

[9] Litvin F L, Chen N X, Lu J. Computerized design and generation of low-noise helical gears with modified surface topology[J]. Transactions of the ASME, 1995, 117(38): 254−261.

[10] 贾鹏, 许洪斌. 齿轮齿面接触分析TCA技术及发展动态[J]. 长春大学学报, 2006, 16(2): 40−41. JIA Peng, XU Hongbin. On the technology of tooth contact analysis (TCA) and its development tendency[J]. Journal of Changchun University, 2006, 16(2): 40−41

[11] 郭辉, 赵宁, 方宗德, 等. 基于接触有限元的面齿轮传动弯曲强度研究[J]. 航空动力学报, 2008, 23(8): 1438−1442. GUO Hui, ZHAO Ning, FANG Zhongde, et al. Research on bending strength of face-gear transmission based on contact finite element method[J]. Journal of Aerospace Power, 2008, 23(8): 1438−1442

[12] 杨生华. 齿轮接触有限元分析[J]. 计算力学学报, 2003, 20(2): 138−143. YANG Shenghua. Finite element analysis of gear contact[J]. Chinese Journal of Computational Mechanics, 2003, 20(2): 138−143.

[13] 李军. 齿轮副在平面机构分析中的探讨[J]. 机械, 2009, 36(11): 27−29. LI Jun. The discussion of gear pair at the plane mechanism analyzes[J]. Machinery, 2009, 36(11): 27−29.

[14] 贺书乾, 杨惠敏, 魏金营, 等. 机构综合中的高副低代研究[J]. 中州大学学报, 2009, 26(4): 126−128. HE Shuqian, YANG Huimin, WEI Jinying, et al. A research on lower pair replacing higher pair in synthetic mechanism[J]. Journal of Zhongzhou University, 2009, 26(4): 126−128.

[15] 牛鸣岐. 平面机构高副低代原理的证明[J].贵州工业大学学报(自然科学版), 1999, 28(4): 62−64. NIU Mingqi. The proof of the principle of a higher-pair replaced by lower-pairs in a plane mechanism[J]. Journal of Guizhou University of Technology (Natural Science Edition), 1999, 28(4): 62−64.

(编辑 罗金花)

Transmission principle and geometric design method of face contact gear

SONG Hongzhou, WEI Shimin, LIAO Qizheng, GUO Lei

(School of Automation, Beijing University of Post and Telecommunications, Beijing 100876, China)

In order to enlarge the contact area between the gear and the tooth surface and reduce the stress, a transmission method was proposed based on face contact gear. According to the lower pair replacing higher pair principle, the point contact or line contact of the tooth surface were turned into face contact with the adding of a sliding block and the changing of the shape of the tooth profile. The kinematic model of the internal and external meshing transmission was established based on the complex number vector method, and the equations of transmission ratio, angular velocity and angular acceleration were derived. The characteristics of continuous transmission and the relative position between the tooth profile and the slide block were analyzed, and the critical condition of selecting between a driving gear and a driven gear was obtained. Meanwhile, the teeth number selection range was further discussed under different situations. Furthermore, the structure design and simulation analysis of face contact gear transmission was gotten with three-dimensional modeling tool. The results show that the simulation results of the face contact gear transmission coincide with those of the theoretical prediction. Thus, a theoretical basis is provided for the promotion and application of surface contact gear transmission.

gear; face contact; meshing; sliding block; lower pair replacing higher pair

10.11817/j.issn.1672-7207.2015.09.012

TH132.4

A

1672−7207(2015)09−3245−07

2014−11−29；

2015−01−28

国家高技术研究发展计划(863计划)项目(2011AA040203)；国家科技支撑计划项目(2013BAD17B06)；粮食公益行业科研专项(201313009-06) (Project(2011AA040203) supported by the National High Research Development Program (863 Program) of China; Project(2013BAD17B06) supported by National Science and Technology Support Program of China; Project(201313009-06) supported by Special Funds for Grain Research in the Public Interest)

魏世民，教授，博士生导师，从事机械传动及机械设计研究；E-mail: wsmly@bupt.edu.cn