基于混合Petri网的单点信号优化感应控制

牟海波，俞建宁，刘林忠



基于混合Petri网的单点信号优化感应控制

牟海波，俞建宁，刘林忠

(兰州交通大学交通运输学院，甘肃兰州，730070)

为研究单交叉口交通信号感应控制问题，建立由连续Petri网描述交通流和离散Petri网描述交通信号控制的混合Petri网模型。根据连续Petri网的离散化方法，以连续Petri网中的参数为基础，提出各个相位车辆总停留时间的计算方法。为优化各个相位的绿灯时间，以车辆总停留时间最小为目标建立优化感应控制模型，并进行仿真计算。研究结果表明：采用基于混合Petri网的优化感应控制方法时，4个相位的车辆平均延误分别为18.19，15.65，14.88和15.24 s，与基于混合Petri网的一般感应控制方法、基于离散Petri网的感应控制方法相比较，平均延误的最大缩短率分别为26.26%和38.33%。基于混合Petri网的优化感应控制方法可以较好地实现单点信号控制。

交通信号控制；优化感应控制；建模仿真；混合Petri网；平均延误

随着交通需求的不断增加，城市交通问题更加严重。因为疏于管理与控制，现有道路的使用效率较低是导致发展中国家城市交通拥挤的主要因素。平面交叉口的通行能力通常远低于路段的通行能力，因此，交叉口是城市交通运输的瓶颈，也是事故和延误的根源。为保障交通安全与畅通，提高现有设施的通车效率，交通管理成为主要手段，其中最基本的方法是通过建立高效的交通信号控制系统，得到科学合理的交叉口交通信号控制方案。感应控制是根据交叉路口进口道车流的变化进行信号实时控制的一种信号控制方式，适合于交通流量随机波动较大的交叉口。经典的感应控制机理无法充分利用绿灯时间，因此，一些学者对感应控制的配时进行了深入研究。Akcelik[1]针对固定的间隔时间，讨论了到达车辆的车头时距分布情况，提出了感应控制下平均绿灯时长及周期时长的估计方法，为感应控制的时间设置优化提供重要的参考信息；Rouphail等[2]针对美国道路通行能力手册(HCM)延误模型的局限性，利用TRAF-NETSIM系统和现场数据对感应控制广义延误模型进行评估，结果表明该广义延误模型对交通流量及感应控制器设置的变化反映敏感，更适用于估计感应信号控制下的车辆延误；Viti等[3]针对感应控制下车辆到达的动态随机特性，以概率论为基础，提出了一种含有较少参数且将延误和等待时间作为时间依赖过程加以量化估计的感应控制模型；郭谨一等[4]以大量实际调查数据为基础, 运用Synchro软件对北京市典型十字交叉口在采用感应信号控制前后的延误、交叉口服务水平等数据进行了对比，说明了感应信号控制在轻交通量交叉口或轻交通量期间的有效性；Zhang等[5]建立了随机模型，通过实时队长和各个相位的交通流到达特性来动态优化感应控制中的最小和最大绿灯时间，并利用VISSIM仿真软件验证了所提出算法的效果；邵峰等[6]为减少车辆延误，提高通行能力，研究了在单路口感应控制系统中确定合理单位绿灯延时的方法；邵锦锦等[7]针对经典感应控制算法的局限性，提出一种动态相序的多相位感应控制算法，并验证了算法的有效性；Zheng等[8]提出了感应控制中确定最优控制参数的实时控制模型，模型中包含了预测到达率和转弯比率的流量预测过程，通过逐个周期的动态优化信号控制参数来满足预测的需求；Xhevat等[9]分析对比了固定信号控制和半感应信号协调控制下主干道的服务水平，并采用HCM和Synchro/Sim交通软件优化信号控制参数。然而，交通流的连续特性及交通信号的离散特性使得城市交通系统成为一个混合系统，选择一种恰当的模型来精确描述该系统的动态行为且便于仿真计算尤为重要[10]。Petri网所建的模型直观、易于理解，模型中的参数具有深刻的数学内涵，在描述混合系统方面有无可比拟的优势，因此，基于Petri网的模型很适合描述城市交通系统的信号控制问题及进行仿真计算。1994年，一般Petri网首次被应用于交叉口交通信号控制问题中，之后一些专家和学者开始采用各种类型的Petri网模型如连续Petri网、混合Petri网、着色Petri网等研究城市交通信号控制问题[11−18]，然而很少研究感应控制。尽管DiCesare等[11]采用离散Petri网方法，考虑根据当前相位的车辆到达情况延长绿灯时间，但是没有考虑其他相位的车流情况，因此，无法保证系统最优。本文作者针对经典感应控制无法充分利用绿灯时间尤其是绿灯延长时间的缺点，提出一种基于混合Petri网的固定相序优化感应控制方法，通过连续Petri网的离散化方法，以最小化系统内所有车辆的平均延误为目标，对各个相位的最佳绿灯时间进行优化，从而确定当前相位的绿灯时间，即改变相位的最佳时机。

1 混合Petri网基本理论

混合Petri网是由，，，，构成的1个五元组[13]，其中：

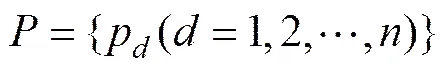
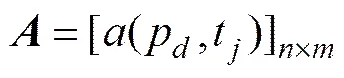
式中：为有限的库所集，可分为P和P2部分，分别为离散库所和连续库所；为有限的变迁集，可分为T和T2部分，分别为离散变迁和连续变迁，且，；和为前向关联函数矩阵与后向关联函数矩阵；为库所的标识向量，离散库所的标识为非负整数，而连续库所的标识为非负实数；p为库所集中的第个库所；t为变迁集中的第个变迁；(p,t)为t与其输入库所p之间弧上的权值；(p,t)为t与其输出库所p­之间弧上的权值，当p为离散库所和连续库所时，权值分别为非负整数和非负实数；(p)为库所p的标识，标识用托肯表示。

变迁t的输入和输出库所集用1j和2j表示，库所p­的输入和输出变迁集用1d和2d表示。据，对于离散变迁t，若均有(p)大于0，则t成为使能的变迁且立即被触发。t触发后，所有输入库所的标识变化为，所有输出库所的标识变化为。对连续变迁t，在均有(p)不小于的前提下，若有(p)大于0，则称t为强使能，若(p)等于0，则称t为弱使能。连续变迁t的触发不是一个瞬时动作，而是以非负实速度持续发生，可构成一个连续的过程。

若离散变迁的触发时间为0 s，则为瞬时变迁；若触发时间大于0 s，则为时延变迁。在用图形表示混合Petri网时，实心矩形和短线分别表示时延和瞬时离散变迁；空心矩形表示连续变迁；离散和连续库所分别用1个圆和2个同心圆表示，托肯用小黑点表示。

2 基于混合Petri网的交叉口感应控制模型

图1所示为信号控制交叉口车流方向及相位。图1(a)所示为城市交通网络中的交叉口，各方向交通流均由左转、直行、右转车流构成，1至8方向车流为进入交叉口的车流，9至12方向车流为离开交叉口的车流。采用的4相位信号控制方案如图1(b)所示。以当前相位为第1相位为例，建立交叉口混合Petri网模型如图2所示。该模型由连续Petri网和离散Petri网2部分组成，连续Petri网描述交通流变化情况，离散Petri网描述交通信号控制方案。

(a) 交叉口交通流；(b) 相位

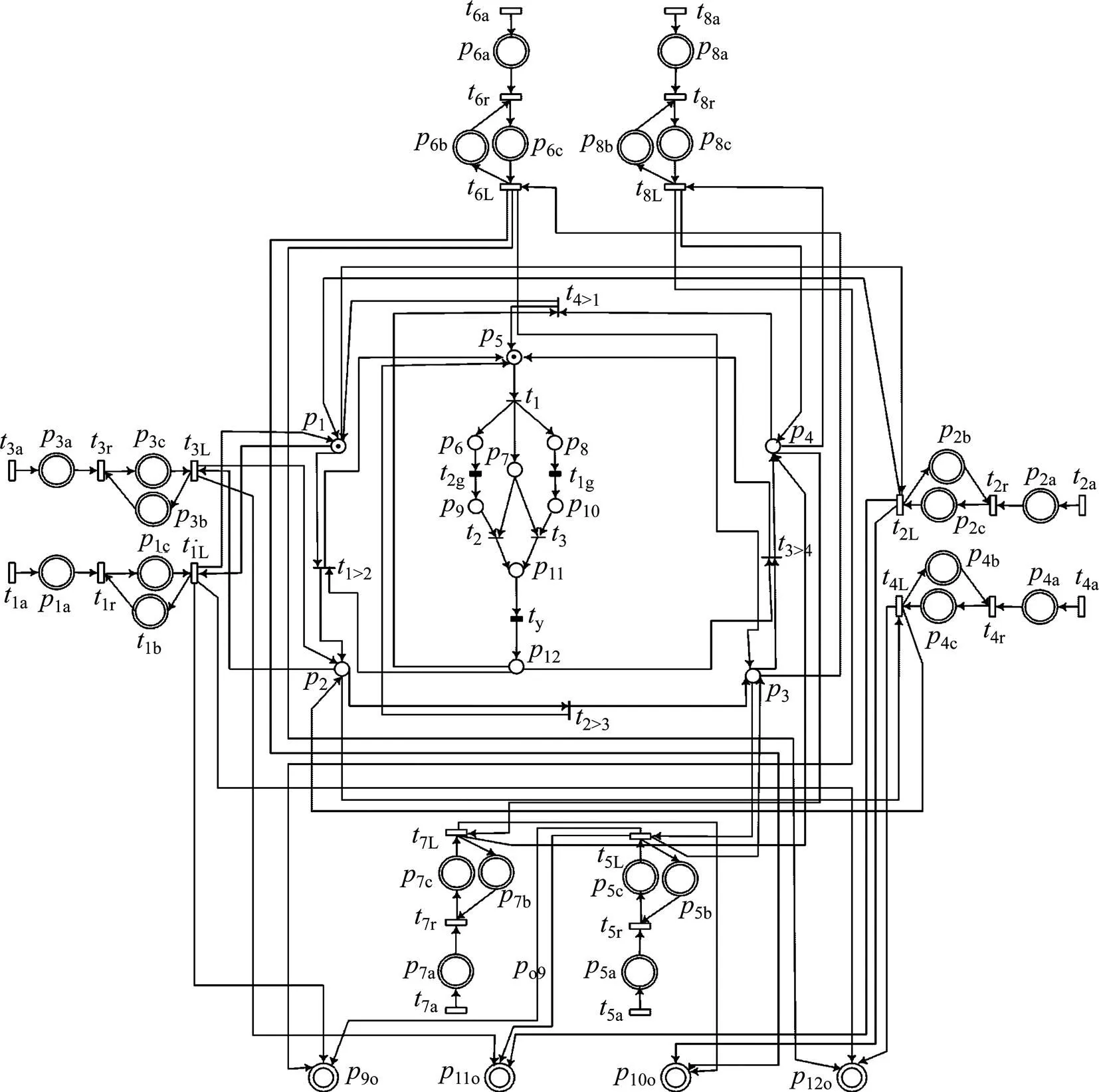
图2 交叉口混合Petri网控制模型

在连续Petri网部分，库所pa，pb和pc分别代表方向等待进入交叉口的车流、检测区内的车流以及检测区剩余位置数，=1, 2, …, 8；库所po的标识代表从方向离开交叉口的车流，=9, 10, 11, 12；变迁ta，tr和tL一旦被触发，代表方向的车流到达、车流进入检测区以及车流离开交叉口，=1, 2, …, 8。

在离散Petri网部分，库所1，2，3和4一旦得到托肯，表示当前相位是第1，2，3和4相位，5为含有初始托肯的库所；变迁1g，2g和y一旦被触发，代表实际绿灯时间结束、最大绿灯时间结束及黄灯时间结束；变迁一旦被触发，则由相位转换到相位。以从第1相位到第2相位为例说明相位转换过程。在初始状态下，1中的托肯允许1和2方向车流通过交叉口，5中的托肯使瞬时变迁1立即被触发，6，7和8各得到1个托肯。分别用1，2和3表示最短绿灯时间、实际计算绿灯时间和最长绿灯时间。若2＜3，则经过2时间后，1g被触发，8失去托肯，10得到托肯。7和10中的托肯使瞬时变迁3立即被触发，11得到托肯。若2≥3，则经过3时间后，2g被触发，6失去托肯，9得到托肯。7和9中的托肯使瞬时变迁2立即被触发，11得到托肯。由于7是变迁2和3的输入库所，因此，2被触发将使7失去托肯，从而限制了变迁3的触发。同样，变迁3被触发也将使得2不能被触发。用表示黄灯时间，一旦11得到托肯，经过后y被触发，黄灯时间结束，12得到托肯。1和12中的托肯使瞬时变迁立即被触发，2和5得到托肯，2中的托肯使得第2相位车流通过交叉口，5中的托肯使得交通信号重新进入从第2相位到第3相位的转换过程。

3 单点信号优化感应控制模型

为进行仿真计算，必须将连续Petri网离散化，采用Júlvez[14]提出的离散化方法，该方法的优点是连续Petri网的性质不会被破坏。若表示阶段通过变迁t的平均流量，v表示变迁t的最大触发速度，表示阶段开始时库所p的标识，则

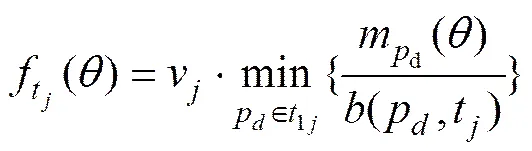
(2)

式中：为托肯流矩阵，等于前相关联函数与后相关联函数的差值；为离散化后各个时间段的长度。

首先计算当前绿灯相位的车辆总停留时间，定义e为绿灯延长时间，以第1相位为例，在e时间段内，当前绿灯相位的车辆总停留时间T为

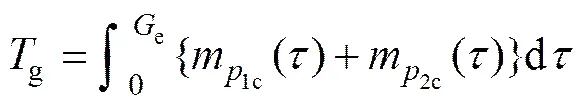
由于

(4)

故

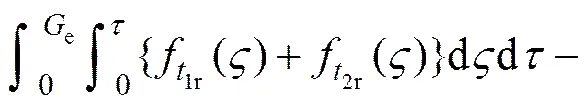
(6)

由于最小绿灯时间结束后才会转入绿灯延长时间，因此，可将最小绿灯时间结束的时刻看成绿灯延长时间的起始时刻，故令，，有

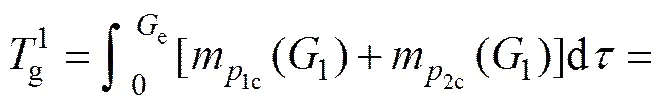
(7)

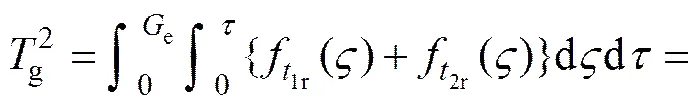
(8)

将式(8)离散化，并根据定积分的公式，有

(9)

据类似的方法可得

(10)

e时段内所有红灯相位的车辆停留时间之和h为

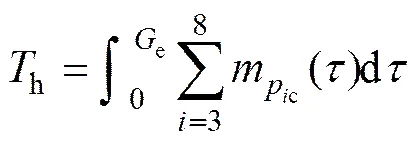
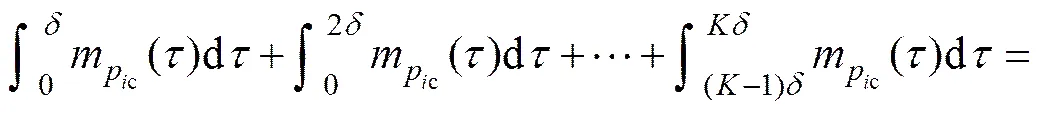
(12)

所以，

(13)

因此，绿灯相位和红灯相位所有车辆总停留时间为

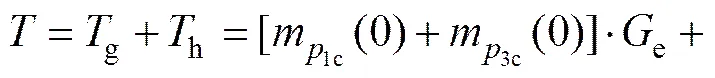
综上所述，可以得到在第1相位为通行相位时，求车辆平均停留时间最小的数学模型为

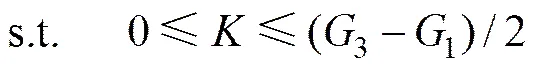
采用类似的方法可以得到第2，3和4相位为通行相位时，车辆总停留时间的表达式以及求车辆平均停留时间最小的数学模型。

4 仿真结果分析

以Matlab和C#为仿真工具，令1，2和分别为10，60和2 s，每个小时间段的长度为2 s。代表车流到达交叉口的变迁1a和2a的最大触发速度为0.33次/m，3a和4a的最大触发速度为0.09 次/m，5a和6a的最大触发速度为0.26次/m，7a和8a的最大触发速度为0.07次/m。代表车流离开交叉口的变迁tL(=1, 2, 5, 6)的最大触发速度为0.50次/m，变迁tL(=3, 4, 7, 8)的最大触发速度为0.30次/m，右转比例为20%。库所pa(=1, 2, …, 8)的初始标识为1，库所pc(=1, 2, 5, 6)的初始标识为5，库所pc(=3, 4, 7, 8)的初始标识为3。

仿真20个信号周期，将本文作者提出的交通信号优化感应控制方法、以图2所示的混合Petri网为基础不进行优化的一般感应控制方法、以及DiCesare等[11]提出的基于离散Petri网的感应控制方法得到的车辆平均延误进行比较，相位1和2的相位延迟计算结果如表1所示，相位3和4的相位延迟计算结果如表2所示。

表1 相位1和2的相位延迟计算结果

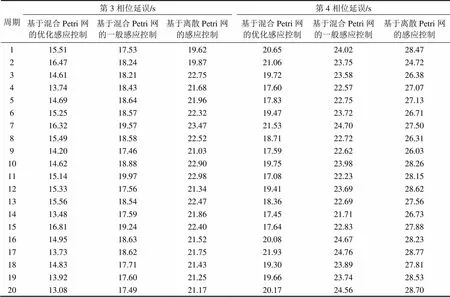
表2 相位3和4的相位延迟计算结果

由表1和表2可以看出：采用基于混合Petri网的优化感应控制方法时，每个相位的车辆平均延误比基于混合Petri网的一般感应控制方法以及DiCesare等[11]提出的基于离散Petri网的感应控制方法的车辆平均延误明显降低。采用基于混合Petri网的优化感应控制方法时，4个相位20个周期的车辆平均延误分别为18.19，15.65，14.88和15.24 s；采用基于混合Petri网的一般感应控制方法时，4个相位20个周期的车辆平均延误分别为21.50，18.19，18.35和23.46 s；采用基于离散Petri网的感应控制方法时，4个相位20个周期的车辆平均延误分别为25.04，19.92，21.81和27.48 s。与基于混合Petri网的一般感应控制方法相比较，本文作者提出的优化感应控制方法中，4个相位车辆平均延误缩短率的平均值分别为15.41%，18.87%，13.91%和18.03%，最大缩短率达26.26%；与基于一般离散Petri网的感应控制方法相比较，本文作者提出的优化感应控制方法中，4个相位车辆平均延误缩短率的平均值分别为27.23%，31.64%，21.36%和29.87%，最大缩短率达38.33%。仿真结果表明：本文作者提出的优化感应控制方法方法明显优于基于Petri网的一般感应控制方法，基于Petri网的优化感应控制方法达到了减少单交叉口车辆延误的目的。

设各相位车辆到达率服从正态分布，当期望分别为900，1 080，1 200和1 440 辆/h，方差均为180辆/h时，各相位绿灯时间如图3~6所示。

由图3~6可见：采用基于Petri网的优化感应控制方法时，为使车辆平均停留时间最小，随着到达率期望的增加，各个相位的绿灯时间增加，继而周期时长增大。当到达率期望值由900 辆/h增至1 440辆/h时，第1和第3相位的绿灯时间最大值分别由20 s和22 s增加到50 s和52 s；第2和第4相位的绿灯时间最大值分别由18 s增加到26 s和28 s；周期时长由78 s增加到150 s。由于第2和第4相位为左转相位，达到率较小，因此，第2和第4相位绿灯时间较第1和第3相位绿灯时间要短。

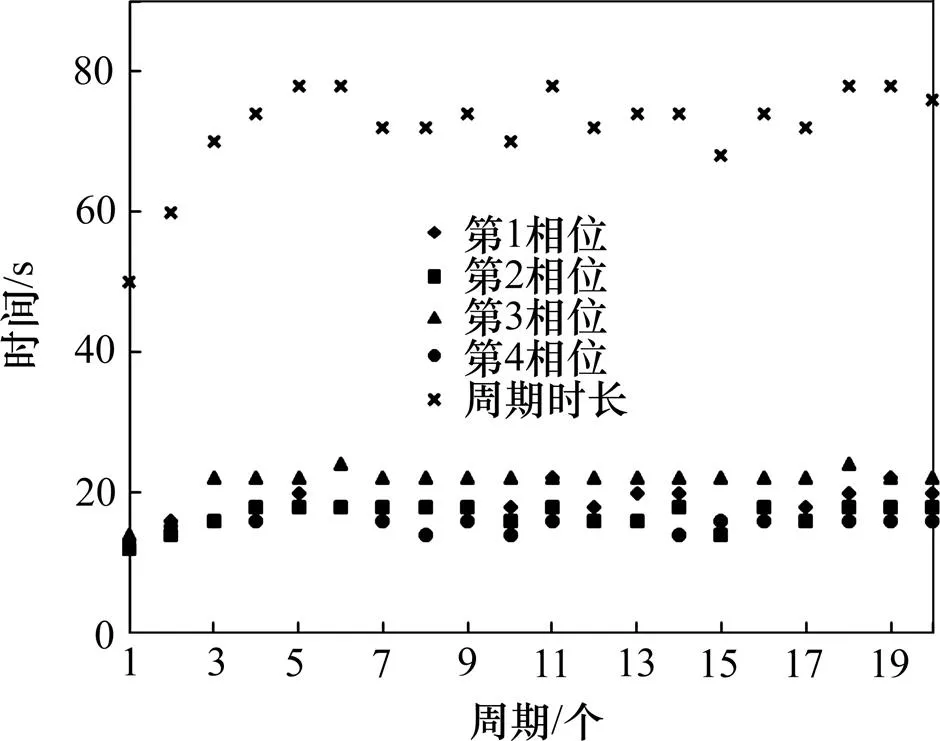
图3 期望为900 辆/h时各相位的绿灯时间

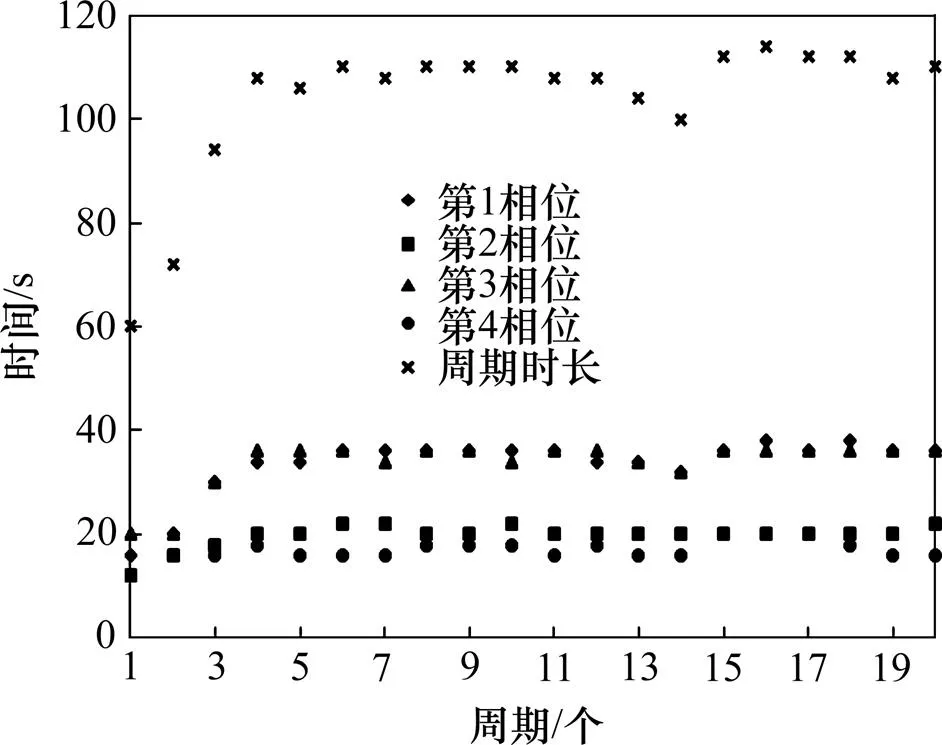
图4 期望为1 080 辆/h时各相位的绿灯时间

图5 期望为1 200辆/h时各相位的绿灯时间

图6 期望为1 440辆/h时各相位的绿灯时间

5 结论

1) 根据城市交通系统是混合系统的特性，利用Petri网在混合系统建模中的优势，结合建模与仿真分析研究单点交叉口信号控制问题，采用离散Petri网描述信号控制、连续Petri网描述交叉口交通流，建立了单点交叉口混合Petri网模型。

2) 为进行仿真计算，根据连续Petri网的离散化方法，以连续Petri网的数量指标为基础，得到了各个相位车辆总停留时间的计算方法，并以车辆总停留时间最小为目标，建立了优化模型。

3) 优化感应控制方法可以较好地实现对单点交叉口的信号控制。

参考文献：

[1] Akcelik R. Estimation of green times and cycle time for vehicle-actuated signal[J]. Transportation Research Record, 1994, 1457: 63−72.

[2] Rouphail N M, Anwar M, Fambro D B, et al. Validation of generalized delay model for vehicle-actuated traffic signals[J]. Transportation Research Record, 1997, 1572: 105−111.

[3] Viti F, Vanzuylen H J. A probabilistic model for traffic at actuated control signals[J]. Transportation Research Part C: Emerging Technologies, 2010, 18(3): 299−310.

[4] 郭谨一, 刘爽, 陈绍宽, 等. 基于Synchro的感应信号控制交叉口仿真研究[J]. 交通运输系统工程与信息, 2004, 4(4): 68−72. GUO Jinyi, LIU Shuang, CHEN Shaokuan, et al. Study on actuated signal controlled intersection a synchro-based[J]. Journal of Transportation Systems Engineering and Information Technology, 2004, 4(4): 68−72.

[5] ZHANG Guohui, WANG Yinhai. Optimizing minimum and maximum green time settings for traffic actuated control at isolated intersections[J]. IEEE Transactions on Intelligent Transportation Systems, 2011, 12(1): 164−173.

[6] 邵峰, 查伟雄. 基于单路口感应控制系统的单位绿灯延时研究[J].华东交通大学学报, 2008, 25(1): 37−40.

SHAO Feng, ZHA Weixiong. Research on the extension green time based on actuated-control system for isolated intersection[J]. Journal of East China Jiaotong University, 2008, 25(1): 37−40.

[7] 邵锦锦, 陈锋, 孙欣欣, 等. 多相位感应控制配时方案的优化设计[J]. 计算机系统应用, 2011, 20(1): 48−51. SHAO Jinjin, CHEN Feng, SUN Xinxin, et al. Optimization design of multi-phase inductive control plan[J]. Application of Computer System, 2011, 20(1): 48−51.

[8] ZHENG Xing, Recker W, CHU Lianyu. Optimization of control parameters for adaptive traffic-actuated signal control[J]. Journal of Intelligent Transportation Systems: Technology, Planning, and Operations, 2010, 14(2): 95−108.

[9] Xhevat P, Arlinda A. A sample of semi-actuated traffic control versus fixed-time traffic control[J]. Journal of Mechanics Engineering and Automation, 2013, 3(5): 334−337.

[10] 牟海波, 俞建宁,刘林忠. 基于Petri网的城市主干道信号协调优化[J]. 交通运输工程学报, 2013, 13(2): 106−113. MU Haibo, YU Jianning, LIU Linzhong. Traffic signal coordinated optimization on urban arterial road based on Petri net[J]. Journal of Traffic and Transportation Engineering, 2013, 13(2): 106−113.

[11] DiCesare F, Kulp P T, Gile M, et al. The application of Petri nets to the modeling, analysis and control of intelligent urban traffic networks[M]. Application and Theory of Petri Nets, Heidelberg: Springer Berlin Heidelberg, 1994: 2−15.

[12] Tolba C, Lefebvre D, Thomas P, et al. Continuous and timed Petri nets for the macroscopic and microscopic traffic flow modeling[J]. Simulation Modeling Practice and Theory, 2005, 13(5): 407−436.

[13] Di Febbraro A, Sacco N. On modeling urban transportation networks via hybrid Petri nets[J]. Control Engineering Practice, 2004, 12(10): 1225−1239.

[14] Júlvez J, Boel R K. A continuous Petri net approach for model predictive control of traffic systems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 2010, 40(4): 686−697.

[15] Jbira M K, Ahmed M. Computer simulation: a hybrid model for traffic signal optimization[J]. Journal of Information Processing Systems, 2011, 7(1): 1−16.

[16] Barzegar B, Ghanbari S, Bozorgi H, et al. Modeling and simulation of traffic lights and controller unit systems by colored Petri net[J]. International Journal of the Physical Sciences, 2011, 6(34): 7760−7770.

[17] Barzegar S, Davoudpour M, Meybodi M R, et al. Formalized learning automata with adaptive fuzzy coloured Petri net: an application specific to managing traffic signals[J]. Scientia Iranica D, 2011, 18 (3): 554−565.

[18] 袁绍欣, 赵祥模,安毅生. 无信号交叉口车流通行状况的混杂Petri网模型[J]. 中国公路学报, 2010, 23(1): 93−97. YUAN Shaoxin, ZHAO Xiangmo, AN Yisheng. Hybrid Petri net model of passing conditions of traffic flow at non-signalized intersections[J]. China Journal of Highway and Transport, 2010, 23(1): 93−97.

Optimization of traffic signal actuated control at isolated intersection based on hybrid Petri net

MU Haibo, YU Jianning, LIU Linzhong

(School of Traffic and Transportation, Lanzhou Jiaotong University, Lanzhou 730070, China)

To study the traffic signal actuated control at isolated intersection, a hybrid Petri net model consisting of a continuous Petri net model for modeling traffic flow and a discrete Petri net model for describing traffic signal control was presented. According to the discretization method of continuous Petri net, the formula of total vehicle residence time of each phase was presented based on the parameters of continuous Petri net. To optimize the green time of each phase, taking the minimal average vehicle residence time as objective, a mathematical model for the optimization of actuated control was established, and a simulation calculation was carried out. The results show that by adopting the optimization method of actuated control based on hybrid Petri net, average delay time of four phases is 18.19, 15.65, 14.88 and 15.24 s, respectively. Compared with a general actuated control method based on hybrid Petri net and an actuated control method based on discrete Petri net, the maximal shortening rate of average delay time is 26.26% and 38.33%, respectively. So, the optimization method of actuated control based on hybrid Petri net can better realize signal control of traffic light at isolated intersection.

traffic signal control; optimization of actuated control; modeling and simulation; hybrid Petri net; average delay

10.11817/j.issn.1672-7207.2015.07.047

U491.51

A

1672−7207(2015)07−2727−08

2014−11−06；

2015−01−30

国家自然科学基金资助项目(71361018，71161016)；甘肃省财政厅基本科研业务费资助项目(213058)；甘肃省科技支撑计划项目(212248)；兰州交通大学青年基金资助项目(2011023) (Projects(71361018, 71161016) supported by the National Natural Science Foundation of China; Project(213058) supported by the Fundamental Research Funds of Department of Finance ofGansu Province; Project(212248) supported by Science and Technology Support Plan of Gansu Province; Project(2011023) supported bythe Youth Foundation of Lanzhou Jiaotong University)

牟海波，博士，副教授，从事交通信息工程与控制研究；E-mail: mhbmmm@mail.lzjtu.cn

(编辑 罗金花)