动平衡信号的时频分析方法研究

王义君，焦勇，梅禹珊，宫玉琳

（1.长春理工大学　电子信息工程学院，长春　130022；2.长春中国光学科学技术馆，长春　130000）

动平衡信号的时频分析方法研究

王义君1，焦勇1，梅禹珊2，宫玉琳1

（1.长春理工大学电子信息工程学院，长春130022；2.长春中国光学科学技术馆，长春130000）

针对动平衡信号面向去重平衡机应用时存在的非线性、非平稳性以及实时性，本文在分析硬支撑动平衡理论的基础上，以联合时频分析方法对标准工件进行加重获得的动平衡信号为研究对象，分别用短时傅立叶变换（STFT）、Wigner-Ville分布（WVD）、小波变换和Hilbert-Huang变换（HHT）对动平衡信号进行时频分析。仿真结果表明，STFT是基于窗函数变换的分析方法，对信号局部分析能力不足且分析精度不高；WVD虽然具有好的时频聚集性，但对多分量信号存在交叉干扰项；小波变换局部分析能力强且分析精度高，但涉及小波基的选择，对非平稳信号不具有实时性；HHT可根据信号的局部时变特征对其进行自适应分解，最终给出信号的时频谱和幅值谱，能够准确描述动平衡信号的特征，具有很高的时频分辨率和时频聚集性。

STFT；Wigner-Ville分布；小波变换；HHT变换；时频分析

在动平衡系统应用中，转子不平衡量引起的噪声严重影响设备安全、可靠运行，因此，对转子的动平衡校正是重要的环节［1］。首先需要在动平衡系统工作时，采用检测设备对动平衡信号进行数据采集；其次，利用信号分析理论对动平衡信号特征进行特征分析；最后，根据分析结果提取转子振动信号的幅值和相位信息，确定转子不平衡量的位置，进行不平衡量的校正［2］。其中，对动平衡信号特征进行特征分析是整个过程的核心，分析方法的不同决定了后续校正的准确性［3］。以傅立叶变换为理论基础的传统分析方法，将时域信号映射到频域信号，揭示了信号能量的分布特征。然而，以正弦波及高次谐波为标准基的傅立叶变换，是全局性的信号分析方法，在时域和频域不能同时兼顾的矛盾对信号分析有了局限性，而且傅立叶变换主要用来分析平稳信号，对非平稳信号却无能为力。在实际应用中，往往需要分析信号频率和幅值随时间变化的实时信息，这些信号通常为非平稳信号，探索非平稳信号的分析方法对设备安全运行具有至关重要的作用。动平衡系统工作的环境复杂，由不平衡量引起的动平衡信号是一种非线性、非平稳的实时信号，需要用时频分析方法进行数值解析［4］。

时频分析方法将时间域和频率域的信息特征结合起来，通过信号瞬时频率和幅值来建立信号的能量分布，对能量分布进一步分析可以掌握信号频率和幅值随时间变化的实时信息。根据动平衡信号的特点，分别用STFT（Short-Time Fourier Transform）、Wigner-Ville Distribution（WVD）、Wavelet Transform（WT）和Hilbert-Huang Transform （HHT）方法对实测动平衡信号进行时频分析，主要分析对象为信号高低频局部信息、分辨率、时频聚集性、信号奇异成分检测及自适应性和动平衡信号的本征函数等方面进行分析。本文在仿真实验的基础上，对上述动平衡信号时频分析方法的比较，得出HHT时频谱更清楚反映了动平衡信号频率、幅值随时间变化的关系，准确反应了动平衡信号的固有特性，是一种更为有效的信号分析方法。

1　硬支撑动平衡理论分析

转子由于主、客观因素而产生的不平衡量是产生振动和噪声的根源，为此需要在旋转时对转子进行不平衡量的校正［5，6］。以刚性转子为研究对象，旋转系统不平衡矢量如图1所示。系统几何尺度a、b、c为常数；m1和m2为左、右平面上的随机不平衡量，与主轴之间的距离分别为r1和r2；不平衡量引起的离心力分别为F1和F2，旋转系统的动反力分别为N1和N2，设转子绕z轴以角速度w旋转。

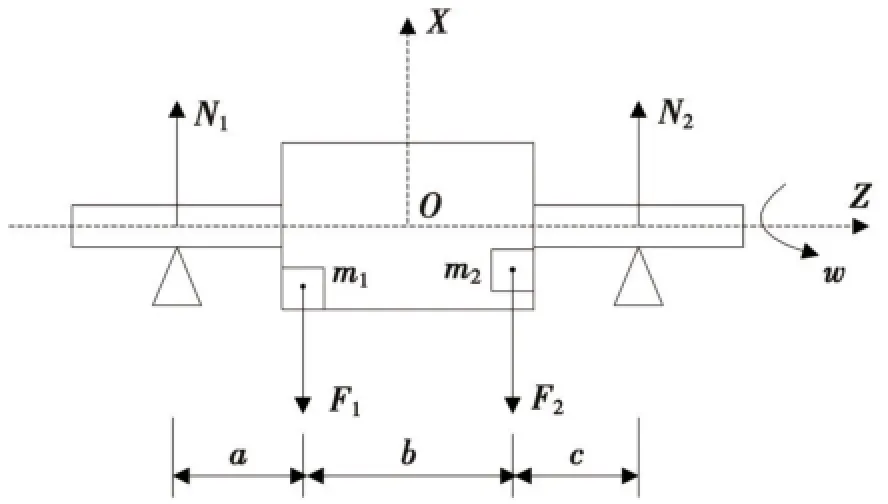
图1　旋转系统不平衡矢量示意图

由图1可知，N1、N2和F1、F2合力等大反向，映射到XOZ平面内：∑M1=0，∑M2=0，即：

同理，映射到YOZ平面内为：

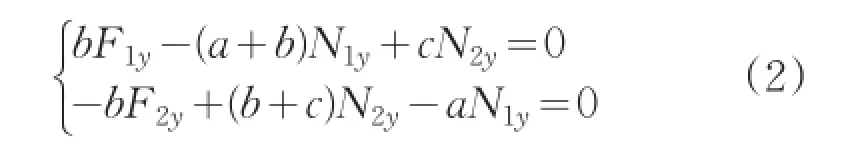
由公式（1）、公式（2）可得：

求解F1、F2可得，

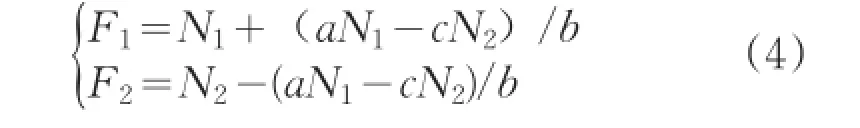
由上述：F1和F2由旋转系统受力情况及几何参数确定，N1和N2可由传感器采集并转换为易处理的电压信号。通过公式（5）确定F1和F2，当测出m1和m2距主轴之间的距离r1和r2时，由公式（1）可得到校正平面上m1和m2的大小。由此可知，对不平衡力的分析间接转化为对动平衡信号的分析。

2　时频分析基本原理

2.1短时傅立叶变换（STFT）

对于非平稳信号，需要研究信号频谱在时间轴上的动态变化，短时傅立叶变换（Short-Time Fourier Transform，STFT）可以满足上述需求，非平稳信号可视为由一系列平稳信号构成，并通过平移窗函数来遍历时间轴，然后分别进行傅立叶变换，构成非平稳信号的时频谱［7］。

设非平稳信号为x（t），h（t）是窄时沿x轴滑动的窗函数，则信号的STFT可定义为：

式中，*表示复数共轭。由于h（t）的时移和频移使STFT可以对信号进行局部分析，且将时域信号函数变换为时间-频率函数。

在工程中应用STFT分析非平稳信号时，信号x（t）可由X（t，w）完全重构来实现，设重构公式为

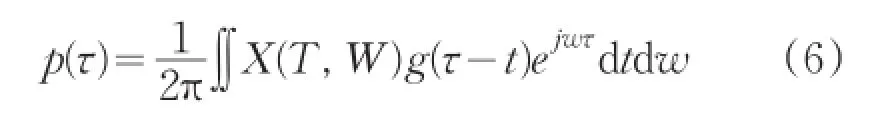
为实现信号x（t）完全重构，则要求h（t）满足∫h*（t）g（t）dt=1。

2.2Wigner-Ville分布（WVD）

设非平稳信号x（t）定义域覆盖整个时域，且为复值，即x（t）∈C，t∈R。则信号的WVD可定义为：

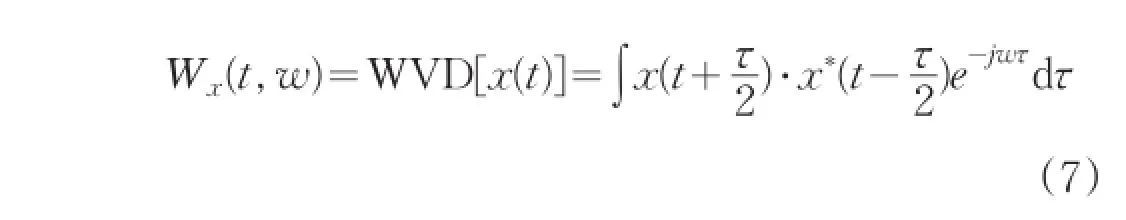
公式（7）可认为是信号x（t）的自相关函数对τ的傅立叶变换，所以信号傅氏谱的WVD可由信号WVD的时间和频率变量互换得到，即WVD的时域和频域具有对称性。

2.3小波变换（WT）

小波变换对非平稳信号分析具有多分辨率分析的特点，在时域和频域可分析信号的局部信息。在低频的频率分辨率比较突出，在高频的时间分辨率比较优越，通常用于分析微弱信号中的奇异成分［8］。

假设Ψ（t）为平方可积函数，即Ψ（t）∈L2（R），其傅氏谱为，且满足重构条件，则称Ψ（t）为母小波。令Ψa，b（t）为小波序列，a为伸缩因子，b为平移因子。则非平稳信号x（t）的小波变换可定义为：

式中，Ψ*（t）表示Ψ（t）的复共轭，其逆变换为：

2.4Hilbert-Huang变换（HHT）

HHT由经验模态分解（Empirical Mode Decomposition，EMD）和希尔伯特谱分析（Hilbert Spectrum Analysis，HAS）组成［9，10］。HHT通过EMD将复合信号抽取为一系列单一频率的本征模态函数（Intrinsic Mode Function，IMF），对IMF进行Hilbert变换，得到信号的时间-频率-能量分布；进一步可得信号的边际谱。HHT在时域上的频率有很高的精度，可以准确表达时频域上的各类信息，这也正是用来分析动平衡信号的依据［11］。

以信号s（t）为例，EMD的筛选过程如下［12］：

（1）找出信号s（t）所有的极大值点和极小值点；

（2）采用三次样条插值拟合信号的上下包络线，求上下包络线均值m1（t）；

（3）原始信号s（t）减去m1（t），得第一个分量h1（t）；

（4）判断h1（t）是否符合IMF条件，若不符合则返回步骤（1）并将h1（t）当作原始信号，重复筛选k次，直到hk（t）满足IMF的条件，即c1（t）=hk（t）；

（5）原始信号s（t）减去c1（t）可得剩余分量r1（t）；

（6）将r1（t）作为新的原始信号，重复步骤（1）到步骤（5），得到新的剩余量r2（t），重复n次，当第n个剩余量rn（t）为单调函数或常数时为止，原始信号s（t）表示为：

通过EMD抽取到IMF分量后，对每个IMF分量做Hilbert变换，可得：

式中，p为柯西主值，通过对ck（t）和（13）式构造解析信号，对相位函数求导可得瞬时频率。因此，原始信号s（t）可以表示为：

式中，信号s（t）的幅值和相位都是时间的函数，可以在三维图上显示信号的幅值和频率随时间变化的特征，即为信号的Hilbert谱。

3　时频分析方法比较

为验证各时频分析方法在分析动平衡信号时的效果，对标准平衡转子通过添加不平衡量进行试验。转子厚度为1.5英寸，半径为4.5英寸，安装在刚性动平衡测量系统上，设置主轴转速为15000rpm，仅在转子的左面放置20克的不平衡量。主轴旋转时，以固定支架上光电编码器产生矩形脉冲的上陡沿作为初始相位和信号采集的触发点，同时两侧的压电传感器采集系统的非平稳振动信号，经过电荷转换、低通滤波、增益调节等转换为适合分析的信号，采用时频分析方法分析动平衡信号的特征。其中采样频率为2000Hz，采样序列长度为1000点，选择采样时间为1000ms的信号进行分析，对其中一路信号进行分析，另一路同理，采集原始振动信号和相应的频域如图2所示。由图2可知，250Hz的基频信号在频域有明显显示，由于600Hz处的高频干扰以及基频附近的谐波干扰严重，其整个频带布满了随机噪声的干扰，使基频信号的信噪比极低，直接分析基频信号显然会造成重大误差，为了更好抑制低频分量和高次谐波的干扰，提高信噪比，本文采用联合时频分析的方法对上述采集到的信号进行分析。

图3为原始振动信号通过短时傅立叶变换后动平衡信号的时频分布特性，STFT基于固定的窗函数来分析信号，选定窗函数的同时，分辨率也随之确定。如需要不同的分辨率分析信号时，则需重新选择窗函数，所以STFT更适合分析分段平稳信号或者近似平稳信号。从信号的三维频谱图和平面图可知：对于非平稳的动平衡信号，在高频部分信号变化剧烈但是轮廓变得模糊，要求窗函数有较高的时间分辨率；在低频部分信号变化较平缓轮廓清晰，但各成分频率叠加严重，要求窗函数有较高的频率分辨率。同时，频率亮度在低频出现频率混叠现象。显然，STFT不能同时满足频率分辨率和时间分辨率最优的需求，其次窗函数选择的不唯一性，对动平衡信号的分析有一定的局限性。

图2　原始振动信号及频谱图

图3　短时傅立叶变换时频分布图

图4所示原始振动信号通过WVD变换后动平衡信号的时频分布特性，从信号三维谱图和平面图可知：WVD分析具有很高的频率分辨率和良好的时频聚集性，信号时频过度集中而出现交叉现象。对于多分量动平衡信号，平面图中低频部分由于交叉干扰而出现难以分辨的情况，使得信号和的分布不再是各自信号分布的和，对于动平衡信号的分析优于DTFT。

图5所示原始振动信号通过WT后动平衡信号的时频分布特性，采用对称的Morlet小波基函数对动平衡信号进行小波谱的分析。由信号三维谱图和平面图可知：小波变换较好反映了信号的局部特征，对信号突变部分也能准确检测；但是信号的高频部分和低频部分存在较大的差异，对信号的时间分辨率和频率分辨率不能同时兼顾，且在整个时频分析过程中自适应性较差，平面图显示频率时间亮度较为清晰。

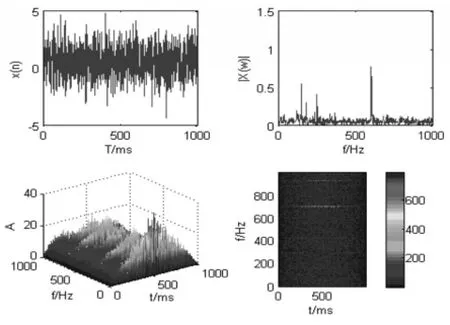
图4　WVD变换时频分布图

图5　小波变换时频分布图

图6为原始振动信号通过HHT变换后动平衡信号的时频分布特性，图6中，（a）为动平衡信号进行EMD分解后的IMF图，imf1和imf2分别对应高频噪声、imf3对应基频信号、imf4和imf5分别对应低频谐波干扰，res为信号趋势项。可见imf更好地反映了动平衡信号的振动模式，清晰显示了各频率分量，基频信号imf3表明动平衡信号的本质特征是一正弦函数；（b）显示了每个imf进行希尔伯特变换后在时频平面上的能量分布-希尔伯特谱，描述了频率随时间变化的详细特征，可直观描述每个时刻信号频率的分布及大小；（c）表示对希尔伯特谱进一步积分得到信号的边际谱，反映了在整个时间轴上，动平衡信号在各频率点处信号幅度的大小，对频率幅度的分析清楚直观；（d）显示了每个imf进行变换后得到的幅度-频率-时间的三维谱图，更清晰地描述了各分量频率在每个时刻的幅值大小及变化趋势，显示了动平衡信号的本质特性及细节成分。层次分明轮廓清晰与前面几种信号分析方法相比，基于HHT的分析方法更能准确、完整、有效的描述动平衡信号。

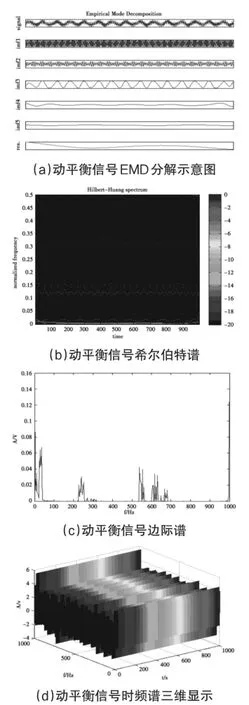
图6　HHT变换时频分布图

4　结论

本文在讨论硬支撑平衡系统理论的基础上，通过对标准平衡转子进行加重采集动平衡信号的方法来验证各种时频分析方法的效果，为进一步提取信息特征奠定理论基础。分析结果表明：STFT不能精确描述信号的局部精度，频率分辨率和时间分辨率之间的矛盾是不可调和的；WVD对信号的局部化精度有很好的描述，时频聚集性最好，但对于多分量的动平衡信号存在交叉干扰项；小波变换较好的抑制了交叉干扰项，但弱化了时频聚集性，且由于不同小波基的选择使信号高频部分和低频部分存在较大差异，在分析信号的过程中缺乏自适应性；相对而言，利用HHT变换能够清晰地给出信号的时频分布情况，EMD分解的imf函数能够准确反映动平衡信号的固有振动模式，对信号时频的分析和特征的描述更直接和有效，该方法为研究动平衡信号的特征提供了新的思想。

［1］ 王晓东，田洪伟，白羽.基于LabWindows/CVI的自动去重平衡系统设计［J］.长春理工大学学报：自然科学版，2003，26（4）：96-98.

［2］ 郭俊华，伍星，柳小勤，等.转子动平衡中振动信号幅值相位的提取方法研究［J］.机械与电子，2011（10）：6-10.

［3］ 李舜铭，郭海东，李殿荣.振动信号处理方法综述［J］.仪器仪表学报，2013，34（8）：1908-1915.

［4］ 逯志宇，王建辉，王大鸣，等.基于遗传算法的时频差快速估计［J］.计算机应用研究，2015，33（1）：1-5.

［5］ 米林，张婧.刚性转子现场动平衡校正方法分析［J］.重庆工学院学报：自然科学版，2008，22（2）：28-32.

［6］ 伍良生，马淑慧，洪豪，等.硬支撑轮胎动平衡机的振动特性研究［J］.机械设计与制造，2014，9（9）：106-108.

［7］ 向玲，唐贵基，胡爱军.旋转机械非平稳振动信号的时频分析比较［J］.振动与冲击，2010，29（2）：42-45.

［8］ 张晗博，殷奕，殷奎喜.基于小波变换的非平稳信号分析与处理［J］.南京师范大学学报：工程技术版，2014，14 （1）：63-69.

［9］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［C］. Proceeding of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences，1998，454（1971）：903-995.

［10］ Huang N E，Wu M L C，Long S R，et al.A confidence limit for the empirical mode decomposition andHilbertspectralanalysis［C］.Proceedingsof the Royal Society of London Series A-MathematicalPhysicalandEngineeringSciences，2003，459 （2037）：2317-2345.

［11］ 徐可君，秦海勤，江龙平.基于EMD和HHT的航空发动机转子—机匣振动信号分析［J］.振动与冲击，2011，30（7）：237-240.

［12］ Huang N E，Wu M L，Qu W D，et al.Applications of Hilbert-Huang transform to non-stationary financialtimeseriesanalysis［J］.AppliedStochastic ModelsinBusinessandIndustry，2003，19（3）：245-268.

Time-frequency Analysis for Dynamic Balancing Signal

WANG Yijun1，JIAO Yong1，MEI Yushan2，GONG Yulin1
（1.School of Electronics and Information Engineering，Changchun University of Science and Technology，Changchun 130022；2.Changchun China Optical Science&Technology Museum，Changchun 130000）

The balancing machine has the problems which include nonlinear，non-stationary and real-time.This paper analyzesdynamicbalancingsignalstime-frequencycharacteristicsbasedonsupportbalancingtheory， whichuses short-time Fourier Transform（STFT），Wigner-Ville distribution（WVD），wavelet transform and Hilbert-Huang transform（HHT）.And dynamic balancing signals obtained by aggravating a joint standard work piece were taken as a research object.The simulation results show that STFT on signal local capacity is insufficient and the responding accuracy is low.Although WVD has a good character of spatial-frequency concentration，multi-component signal crosstalk terms exist.Wavelet transformation has good capacity on signal local and high analysis accuracy，but it is not real-time due to the choice of the wavelet basis.The signal can be adaptively decomposed by HHT according to their local characteristics，resulting in their spectrum and amplitude spectrum.The method can accurately characterize dynamic balancing signals.It has high time-frequency resolution and time-frequency concentration.

STFT；WVD；wavelet transform；HHT；time-frequency analysis

TN98

A

1672-9870（2015）06-0140-05

2015-11-10

吉林省教育厅项目（201576）；吉林省科技厅重点科技成果转化项目（20140307009GX）

王义君（1984-），博士，讲师，E-mail：wyjs-107@163.com