具有半球形凹坑表面的滑动轴承润滑分析
2015-10-12罗星何芝仙
罗星,何芝仙
(1.安徽工程大学 机械与汽车工程学院,芜湖 241000;2.安徽工程大学 力学重点实验室,芜湖 241000)
具有半球形凹坑表面的滑动轴承润滑分析
罗星1,何芝仙2
(1.安徽工程大学机械与汽车工程学院,芜湖241000;2.安徽工程大学力学重点实验室,芜湖241000)
具有非光滑表面的滑动轴承具有一些独特的性质,适当的表面凹坑对径向滑动轴承的润滑性能可能有一定的改善作用。为研究球形凹坑对径向滑动轴承润滑特性的影响,本文建立了具有不同形式球形凹坑的径向滑动轴承润滑分析的数学模型。利用有限差分法进行求解,得到径向滑动轴承的油膜压力与承载力,并研究凹坑的个数、尺寸、分布规律及凹坑深度对径向滑动轴承的润滑特性的影响。计算结果表明:与光滑面相比,在充分润滑状态及轴承几何运动参数不变情况下,合理的凹坑个数、尺寸参数、分布形式及凹坑深度对提高径向滑动轴承的油膜压力及承载能力具有一定的改善作用。
半球形凹坑;油膜压力;Reynolds方程;油膜承载力
径向滑动轴承由于承载能力强,抗震性好,径向尺寸小,寿命长[1]等优点在机械工程中应用广泛。径向滑动轴承安全稳定运转的关键性因素就是润滑油膜的承载能力和油膜压力的分布[2],通过各种途径改善滑动轴承的润滑特性一直是很多学者关注的重要研究课题[3]。研究发现,在摩擦副表面加工出具有一定尺寸和排列的微坑或沟槽能改善滑动轴承摩擦学性能[4-9]。目前,对具有光滑面的滑动轴承的研究已经趋于成熟,但对于具有织构化表面的滑动轴承的润滑分析仍比较薄弱。本文通过建立具有球形凹坑的流体动压润滑分析数学模型,采用数值方法求解,分析凹坑的大小,个数、凹坑深度及分布形式对径向滑动轴承润滑特性的影响,为研究具有仿生表面的滑动轴承润滑特性奠定基础。
1 具有半球形凹坑表面的滑动轴承润滑分析数学模型
1.1Reynolds方程
无论轴承表面具有何种形貌,对于等粘度、等温及定常流动的径向滑动轴承在稳态工作状态下Reynolds方程[10]仍如式(1)所示:
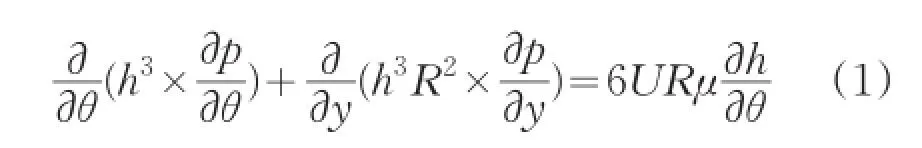
其中:h为油膜厚度,p为油膜压力,R为轴承半径,U为轴承与轴颈相对滑动速度,μ为润滑油粘度,θ为油膜起始角。
1.2光滑表面滑动轴承的膜厚方程
光滑表面滑动轴承的几何模型如图1所示。
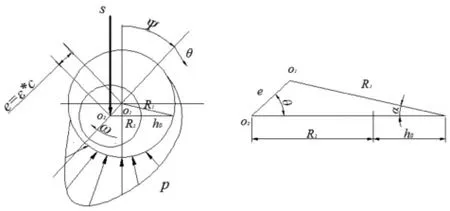
图1 滑动轴承几何模型


1.3具有半球形凹坑的滑动轴承的膜厚方程
具有半球形凹坑表面的轴承表面展开图如图2所示。其结构特点是凹陷面为球面,截面图形为圆形。假设r1为凹坑半径,(x0,y0)为凹坑球心坐标。则具有球形凹坑的径向滑动轴承任意位置的油膜厚度表达式如式(3):
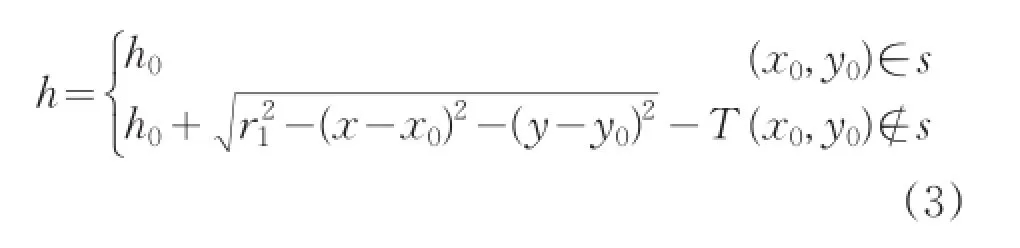

图2 凹坑结构模型
式中,s={(x,y)|(x-x0)2+(y-y0)2>r12}为非凹坑区域,T为凹坑端面到球心的距离。其油膜厚度三维示意图如图3。
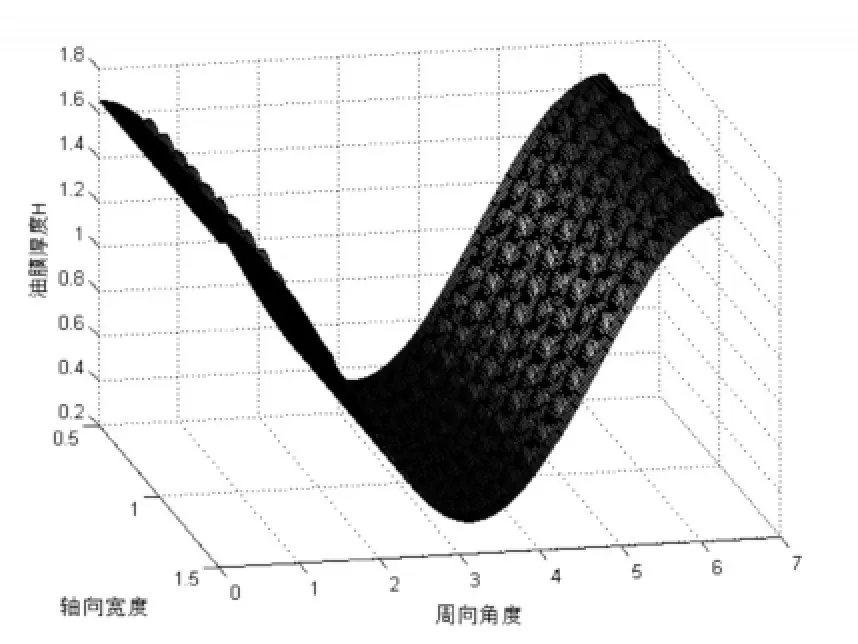
图3 凹坑面径向滑动轴承油膜厚度
1.4边界条件

2 计算步骤及分析方法
(1)输入轴承的几何参数及凹坑的几何参数。
(2)给定滑动轴承的油膜压力初始值p及边界值。
(3)根据(2)和(3)式计算轴承的膜厚。
(4)利用有限差分法求解(3)推导出轴承的油膜压力。
(5)若精度等级符合下式(4),则输出油膜压力值,反之返回步骤(3)。

式中k为迭代次数。
输出油膜力s,计算公式如式(5)。
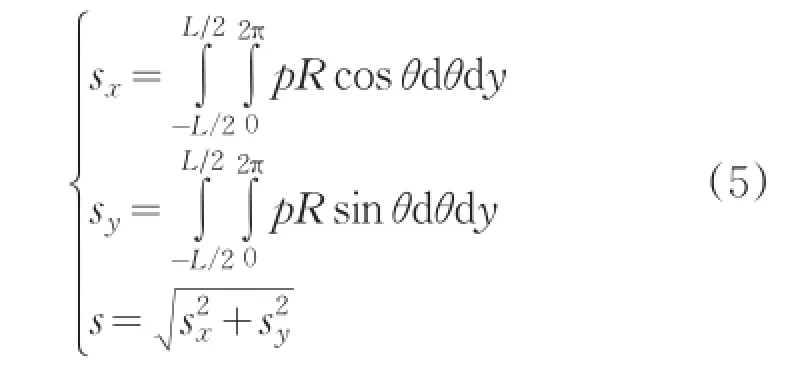
程序框图如图4所示。
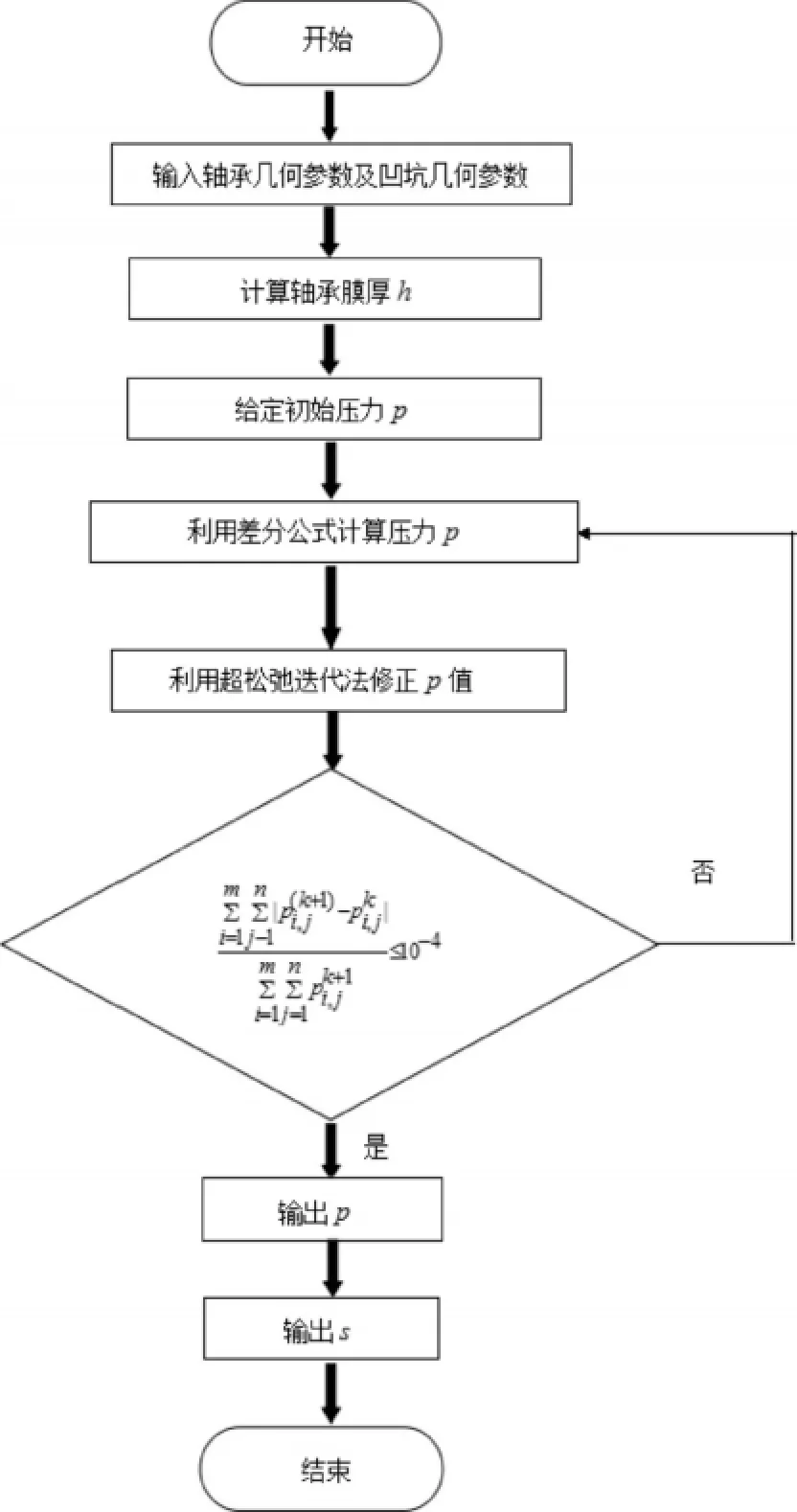
图4 计算流程
3 计算结果及讨论
计算原始数据:轴承半径R=35mm,L=65mm,半径间隙c=0.05mm,润滑油粘度为0.028PaS,轴承与轴颈的相对滑动速度U=0.5m/s。求得轴承的油膜压力及油膜力。
3.1油膜压力和承载力
图5为具有光滑表面的滑动轴承油膜压力分布图,图6为具有半球形凹坑表面(交错分布、凹坑个数为360、凹坑半径为0.04mm)的滑动轴承油膜压力分布图。可见两者油膜压力的变化总趋势基本相同,但光滑面轴承的最大油膜压力为14.97MPa,具有球形凹坑表面轴承的最大油膜压力为16.54MPa,提高了10.5%。其凹坑及其局部区域油膜压力分布如图7所示,可见具有表面凹坑轴承出现凹坑附近油膜压力增高的现象。这是由于球形表面凹坑引起轴承表面楔形效应增强,引起局部油膜压力提升,轴承最大油膜压力提高。计算结果还表明,光滑表面的轴承承载力为29.56kN,表面具有球形凹坑的滑动轴承轴承承载力31.02kN,提高了4.6%。

图5 光滑面油膜压力
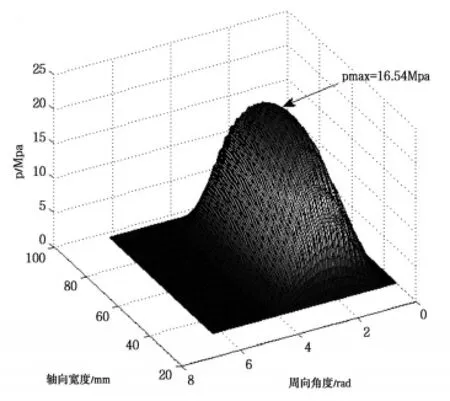
图6 凹坑面油膜压力

图7 单个凹坑局部油膜压力
3.2凹坑的个数、尺寸参数、分布形式及凹坑深度对轴承油膜压力及承载力的影响
图8为半径为0.045mm时具有半球形凹坑表面的滑动轴承最大油膜压力与凹坑数目的关系,可见,最油膜压力随凹坑数目的增加而稍有增加,但变化幅度不大,不超过0.7%。图9为当凹坑数目为360时,滑动轴承的最大油膜压力与凹坑半径的关系。

图8 凹坑数目与最大油膜压力关系
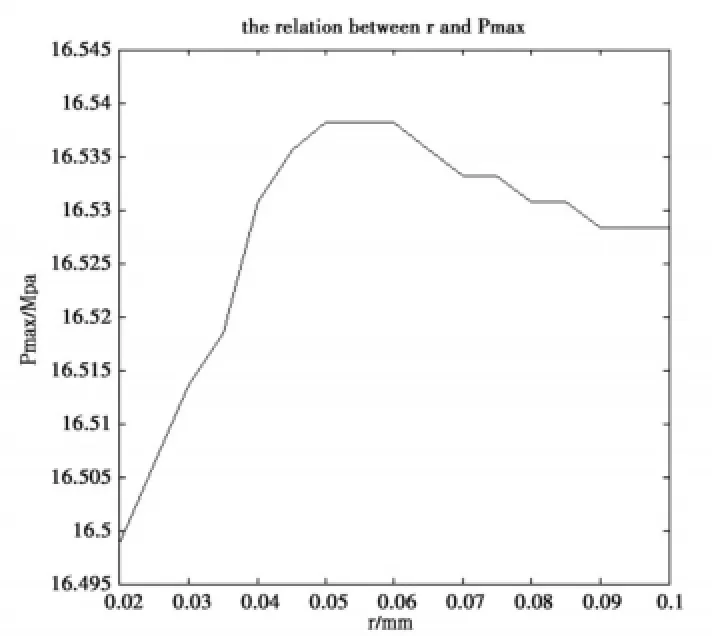
图9 凹坑半径与最大油膜压力关系
图10给出了轴承表面半球形凹坑不同分布形式、个数和凹坑半径与轴承最大油膜压力之间的关系。可见交错分布表面比阵列分布表面轴承的最大油膜压力略有增加,交错分布的最大油膜压力16.542MPa,阵列分布的最大油膜压力为16.416MPa。从图中可以看出,最大油膜压力发生凹坑个数480、半径0.06mm的交错分布情形。

图11 凹坑个数及尺寸对滑动轴承最大油膜压力的影响
图11给出了轴承表面半球形凹坑不同分布形式、个数和凹坑半径与轴承承载力之间的关系。可见其变化趋势与最大油膜压力相同。最大承载力也发生在凹坑个数480、半径0.06mm的交错分布情形,凹坑交错分布时的油膜承载力为31.02kN,凹坑阵列分布时的油膜承载力为30.965kN,仅提高了0.11%。

图11 凹坑个数及尺寸对滑动轴承承载力的影响
图12给出了轴承表面凹坑半径0.06mm、凹坑数量480时滑动轴承的油膜力与凹坑深度的关系。可见,凹坑深度对轴承的承载力影响不大,变化幅度在0.01%以内,可能淹没在计算误差中。

图12 凹坑深度对滑动轴承承载力的影响
综上所述,与光滑面轴承相比,具有半球形凹坑表面的滑动轴承的最大油膜压力和油膜承载力有大幅度提高,合理的凹坑个数、尺寸参数、凹坑深度及分布形式对提高轴承的油膜承载能力也有一定的改善作用,但改善幅度较小。
4 结论
建立具有半球形凹坑表面的滑动轴承流体动压润滑分析计算模型,利用有限差分法求解其油膜压力及油膜承载力的分布规律。计算结果表明:具有半球形凹坑表面的滑动轴承的润滑性能,其交错分布优于阵列分布,最优性能分布为凹坑个数为480,凹坑半径为0.06mm。与光滑表面轴承相比,油膜承载能力提高了4.64%,最大油膜压力提高10.5%。
合理的凹坑个数、尺寸参数、凹坑深度及分布形式对提高轴承的油膜承载能力也有一定的改善作用,但改善幅度较小。
[1] 高庆水,杨建刚.基于CFD方法的液体动压滑动轴承动特性研究[J].润滑与密封,2009,33(9):65-67.
[2] 徐武彬,王镇江,陈其兵,等.基于Sommerfeld数的滑动轴承转子系统稳定性分析[J].中国机械工程,2009,20 (23):2875-2879.
[3] 何芝仙,曹青.计入轴瓦弹性变形的内燃机主轴承润滑分析[J].轴承,2007,62(9):25-28.
[4]Etsion I,Burstein L.A model for mechanical seals withregularmicro-surfacestructure[J].Tribology Transactions,1996,39(3):677-683.
[5]Halperin G,Greenberg Y,Etsion I.Increasing mechanicalsealslifewithlaser-texturedsealfaces [C].15th Int Conf on Fluid Sealing,Maastricht:Mechanical Engineering PUBL,1997.
[6]Etsion I,Kligerman Y,Halperin G.Analytical and experimental investigation of laser-textured mechanical seal faces[J].Tribology Transactions,1999,42 (3):511-516.
[7] Hamilton D B,Walowit J A,Allen C M.A theory of lubrication by micro-irregularities[J].Journal of Basic Engineering,1966,88(1):177-185.
[8] 刘红彬,牛荣军,薛玉君,等.表面纹理对径向滑动轴承油膜承载能力的影响[J].润滑与密封,2010,35(7):19-22.
[9] 于海武,王晓雷,孙造,等.圆柱形微凹坑表面织构对流体动压润滑性能的影响[J].南京航空航天大学学报,2010,42(2):209-213.
[10] 温诗铸,黄平.摩擦学原理[M].北京:清华大学出版社,2012.
Lubrication Analysis on the Journal Bearing with the Semi-spherical Pits Surface
LUO Xing1,HE Zhixian2
(1.Institute of Mechanical and Automotive Engineering,Anhui Polytechnic University,Wuhu 241000;2.Key Lab of Engineering Mechanics,Anhui Polytechnic University,Wuhu 241000)
There are some special function for the journal bearing with non-smooth surfaces.The lubrication performance can be improved when there are proper distributing pits on surface of the bearing.The mathematical model of lubrication analysis is established to study the tribological property of the bearing with semi-spherical pits on its surface. The finite difference method is applied to solve the model.The oil film pressure distribution and the value of load of the bearing can be calculated as well as the relationship is obtained between lubrication behavior of journal bearing and the geometrical property of semi-spherical pits on the bearing surface such as the number,size,depth of pits and the distribution mode.The calculation results show that compared to the smooth surface bearing,the lubrication behavior such as the maximum oil film pressure and the oil film force of the bearing can be improved to some extent for the bearing with semi-spherical pits on the bearing surface working in the sufficient lubrication stable state.
semi-spherical pits;oil film pressure;Reynolds’equation;oil film load of bearing
TH133 31
A
1672-9870(2015)06-0067-05
2015-09-15
国家自然科学基金项目(51575001);芜湖市科技计划项目(2014cxy07)
罗星(1989-),男,硕士研究生,E-mail:460694896@qq.com
何芝仙(1963-),男,博士,教授,E-mail:hezhixian_2004@yeah.net
