T形截面钢骨混凝土异形柱框架抗震性能拟动力试验

杨涛，张喜德，钟海牛，邓志恒



T形截面钢骨混凝土异形柱框架抗震性能拟动力试验

杨涛，张喜德，钟海牛，邓志恒

(广西大学土木建筑工程学院广西防灾与工程安全重点实验室，广西南宁，530004)

制作一榀1/2比例的单跨两层的框架模型，框架由钢筋混凝土(RC)梁和T形截面钢骨混凝土(SRC)异形柱组成。采用拟动力试验方法，通过对框架施加不同峰值加速度的El Centro地震波，研究框架模型的地震响应、耗能等抗震性能。试验结果表明：地震引起的结构损伤主要集中于钢筋混凝土框架梁端部；楼盖处的动力系数介于1.08~2.25之间；框架最大层间位移角满足规范限值的要求；在经历峰值加速度为1 000 cm/s2的地震波作用后，框架抗侧刚度降低了约6%；SRC异形柱框架具有良好的抗震性能，其具备应用于高烈度地震区的可行性。

钢骨混凝土；异形柱；框架；抗震性能；拟动力试验

由于截面形状不规则，钢筋混凝土(RC)异形柱的抗震性能通常比矩形或圆形截面的钢筋混凝土柱的抗震性能差。为了改善RC异形柱的受力性能，通过在柱中配置钢骨(如型钢或钢桁架)便形成了钢骨混凝土(SRC)异形柱。在我国，陈宗平等[1−2]较早开展了对SRC异形柱受力性能的研究。近几年来，SRC异形柱结构的受力性能得到了进一步研究，如邓志恒等[3]对T形截面SRC柱的抗震性能进行了研究，薛建阳等[4−10]对SRC异形柱框架及框架节点的抗震性能开展了拟静力试验研究和有限元分析。上述研究表明，SRC异形柱结构具有良好的受力性能，其抗震性能优于普通RC异形柱结构。目前，在对SRC异形柱结构的抗震性能进行研究时多采用拟静力试验方法，此方法的局限性在于无法反映结构在地震作用下的动力响应。若采用振动台试验研究SRC异形柱结构的抗震性能，则柱中钢骨在模型中难以制作，尺寸效应等因素也会导致试验结果无法真实反映结构的地震响应。拟动力试验结合了拟静力试验和振动台试验的优点，可以较真实地获取结构在地震作用下的动力响应，并已在结构的抗震性能研究领域得到广泛应用[11−16]。为了研究SRC异形柱框架结构在不同峰值地震波作用下的地震响应，本文作者设计1榀1/2比例的由T形截面SRC异形柱与RC梁组成的单跨两层的框架模型，并对其进行拟动力加载试验。在拟动力试验的基础上，结合拟静力试验研究成果，对SRC异形柱框架的抗震性能进行综合评估。

1 试验概况

1.1 试件设计

参照我国抗震设计规范8度设防的标准，设计了1榀1/2比例的单跨两层的框架模型。框架由T形截面钢骨混凝土异形柱和普通钢筋混凝土梁组成，试件的尺寸与配筋如图1(a)所示。异形柱中钢骨由Q235级I10工字型钢加工而成，配钢率(含纵筋)为5.2%。由于型钢表面积较大，为了增强型钢与混凝土的整体工作性能，在型钢之间设置了L30×3的等边角钢，角钢连接件的设置如图1(b)所示。框架模型通过预埋在加载端内的4根直径为24 mm的高强螺杆与两台电液伺服作动器相连接。实测的混凝土轴心抗压强度为25.1 MPa。钢材的力学性能指标见表1。

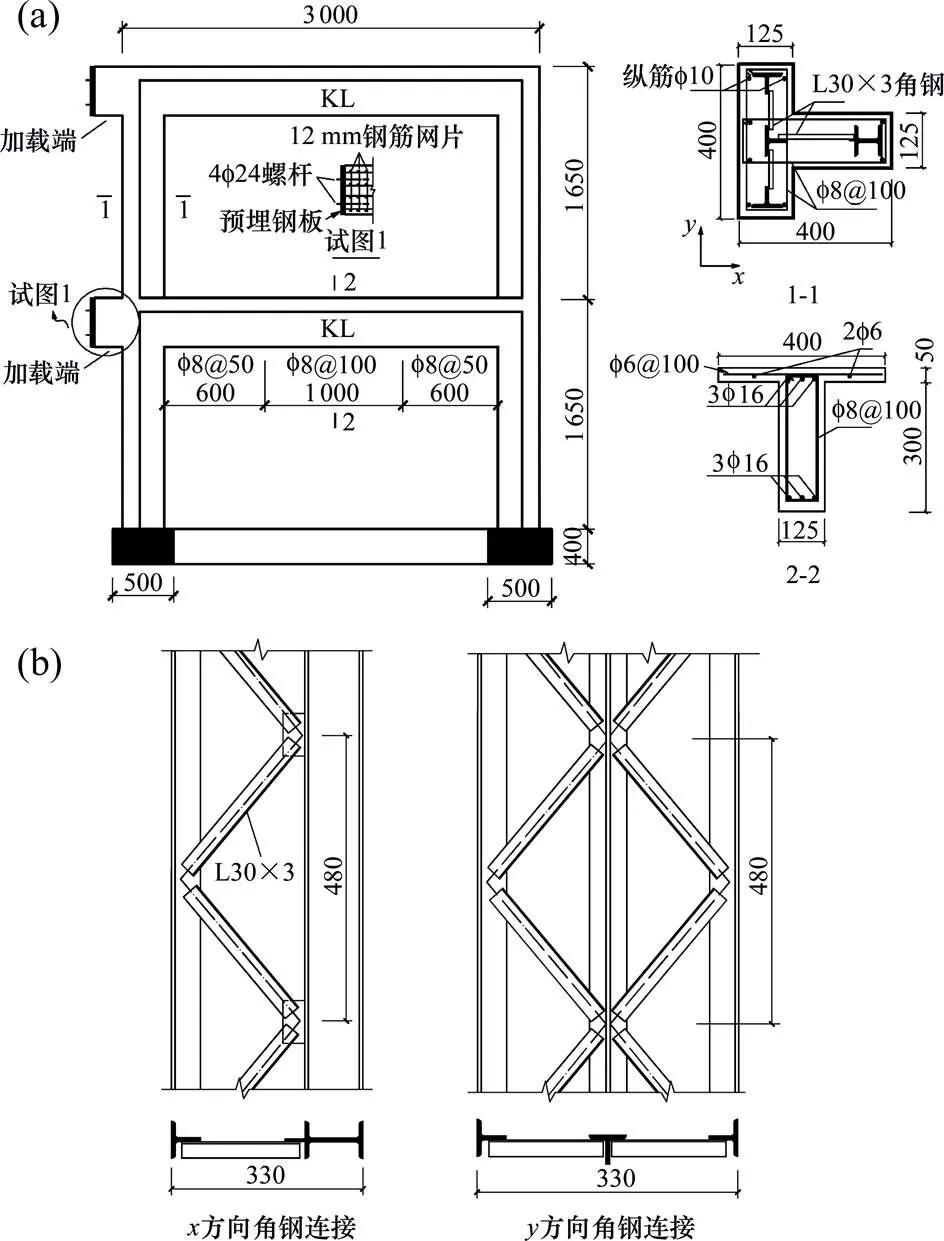
(a) 试件尺寸及配筋；(b) 角钢连接件设置

表1 钢材力学性能

1.2 加载装置

试验中在试件的顶层及底层楼盖处各安装1台行程为±250 mm的电液伺服作动器。为避免荷载作用下试件产生水平刚体位移，在框架模型底部铺垫水泥砂浆，并利用4根钢制反力梁将试件固定于试验台座上。加载装置及主要测量仪器的布置如图2所示，其中速度和加速度传感器用于测量结构的自振频率，位移传感器主要用于实时采集楼盖标高处的位移响应。由于试验条件的限制，未在柱顶施加轴向压力。

图2 加载装置与测点布置

1.3 加载方案

试验加载过程中选用El Centro (N-S)地震波，以考察在长时间地震作用下SRC异形柱框架的地震响应。选取的El Centro地震波共包含900步，步距为0.02 s，地震波总时长为18 s。按照相似条件，地震试验波相邻两数据点的步距调整为0.014 s，总时长调整为12.7 s，调整后的El Centro波如图3所示，其最大波峰为341.7 cm/s2。将地震波的加速度最大波峰分别调整为100，200，400，600和800 cm/s2，用于模拟6度、7度、8度、9度及9度强地震作用[17]。对于不同峰值试验波，结构阻尼比依次取0.05，0.05，0.07，0.09和0.11[18]。在每次试验加载后，利用加载设备实测框架模型的剩余抗侧刚度，并通过动态采集设备测试模型的自振频率。框架模型的阻尼矩阵按照下式计算：

式中：和分别为与阻尼比和结构自振频率相关的常数；，和依次为结构的阻尼矩阵、质量矩阵和刚度矩阵。

图3 El Centro地震波

Fig. 3 El Centro earthquake wave

在确定结构的质量矩阵时，认为层间质量集中于上、下两楼盖标高处，且两质点重力均取80 kN。试验中未在结构上施加配重，而是将质量矩阵输入控制程序；控制程序采用中央差分法进行迭代运算，程序的迭代计算公式如下：

式中：为结构恢复力；为地震波激励作用；和分别为各楼盖处对应的速度和加速度。

2 拟动力试验结果及分析

2.1 试验过程

拟动力试验开始前，输入加速度峰值为50 cm/s2的试验波对框架进行预加载。在验证加载装置和数据采集设备能够正常工作后正式开始试验。

首先，输入加速度峰值为100 cm/s2的试验波，整个加载过程无明显试验现象，也未在试件上发现裂缝。随后，输入加速度峰值为200 cm/s2的试验波，加载过程中在框架梁端部发现了细微的裂缝，其中梁端翼缘板上裂缝宽度相对较大，而在柱上未发现裂缝；当完全卸载时，梁上的裂缝尚可闭合。进一步调整试验波峰值至400 cm/s2，此时在框架梁端产生了新的裂缝，部分裂缝贯穿翼缘板延伸至框架梁的腹板。将试验波加速度峰值调整为600 cm/s2，加载过程中框架梁翼缘上的裂缝宽度有所增加，但梁腹板上裂缝宽度没有明显变化，此阶段仍未在柱上发现裂缝。当输入加速度峰值为800 cm/s2的试验波后，在加载点一侧底层柱脚处柱的翼缘板上发现了若干条沿柱高度方向分布的水平裂缝；同时，在梁柱节点核心区边缘出现了1条斜裂缝。

在经历加速度最大波峰为800 cm/s2的试验波作用后，除了在梁端区域发现一定数量的裂缝外，在框架的其他部位未观测到明显的损伤，故将试验波加速度最大峰值进一步调至1 000 cm/s2。在1 000 cm/s2地震波作用下，框架梁、柱上的裂缝宽度及长度并无明显的变化，试验结束。此时，框架上的裂缝分布如图4所示。

图4 裂缝分布图

2.2 动力系数

在地震作用下，结构加速度响应的最大值与地震波最大加速度之比称为结构的动力系数，它反映了结构对地震波的放大效应。在不同峰值地震波的作用下，框架模型底层和顶层楼盖处最大加速度max及与之对应的动力系数见表2。由表2可知：底层楼盖处的动力系数介于1.08~1.51之间，顶层楼盖处的动力系数介于1.35~2.25之间；随着地震波加速度峰值的增加及结构损伤的积累，楼盖处的动力系数有逐渐降低的趋势。

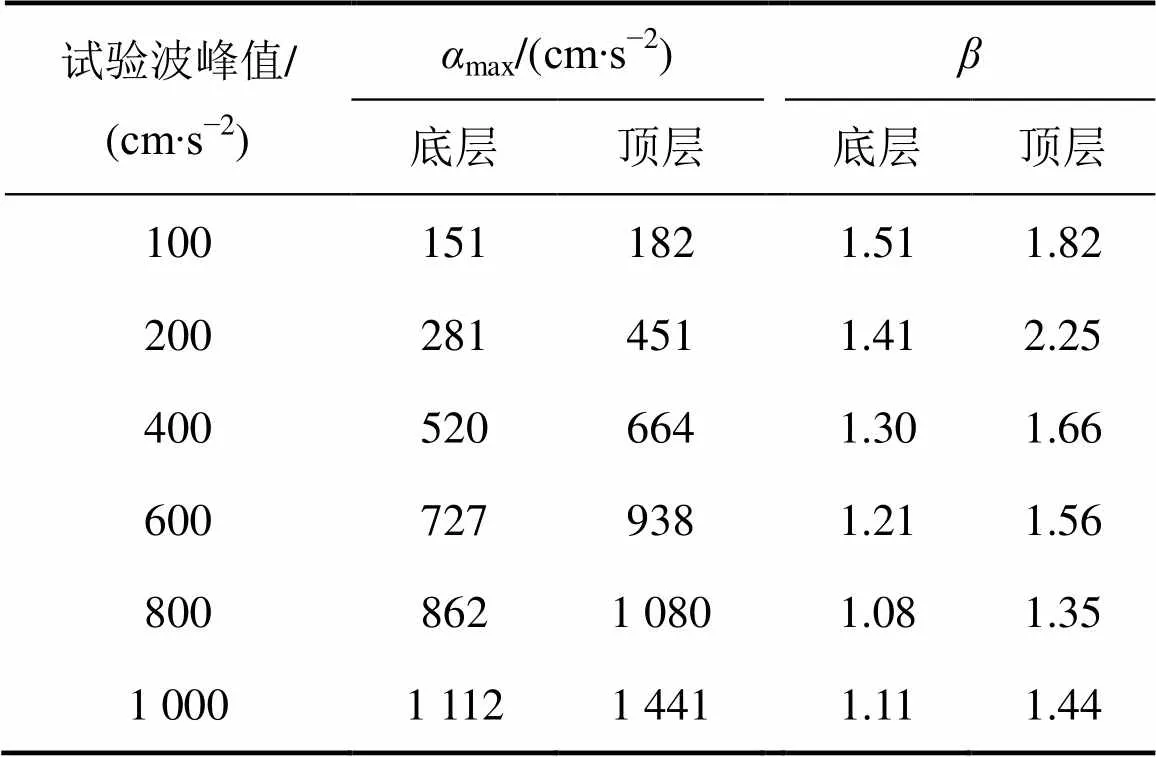
表2 楼盖处加速度峰值

2.3 位移时程曲线

框架顶层楼盖处的位移时程曲线如图5所示。比较可知：随着地震作用的增加，结构的位移峰值逐渐加大；在不同峰值地震波的作用下，结构的位移时程曲线没有发生大的突变，说明损伤未对结构的整体受力性能产生明显的影响。不同峰值地震波作用下试件楼盖处的位移包络图如图6所示。框架模型的最大层间位移角max见表3，对比可知：max可满足《建筑抗震设计规范》[17]和《混凝土异形柱结构技术规 程》[19]的相关限值要求。

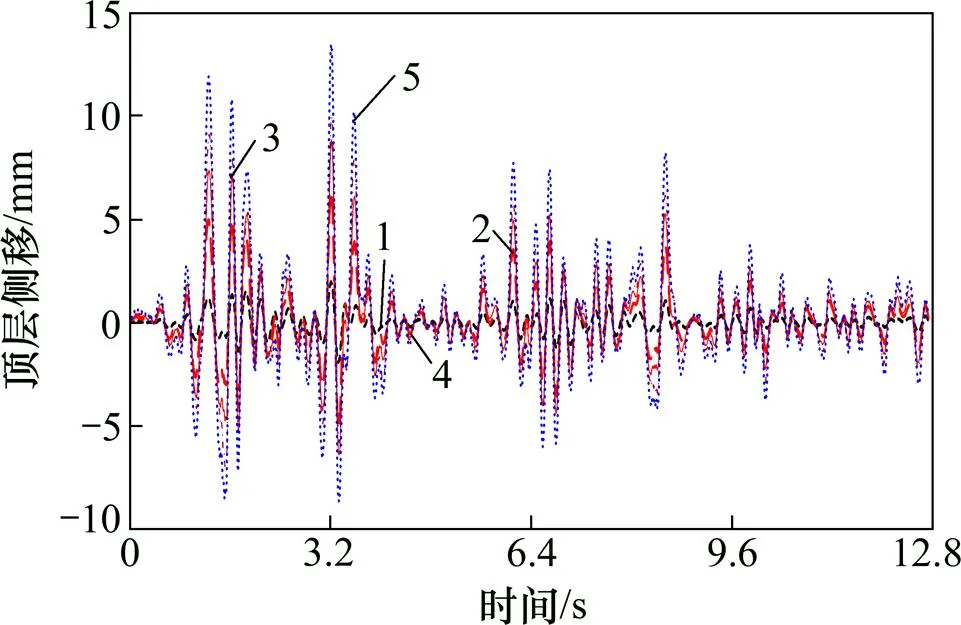
加速度峰值/(cm∙s−2)：1—200；2—400；3—600；4—800；5—1 000

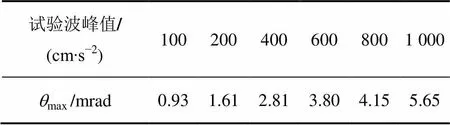
表3 最大层间位移角

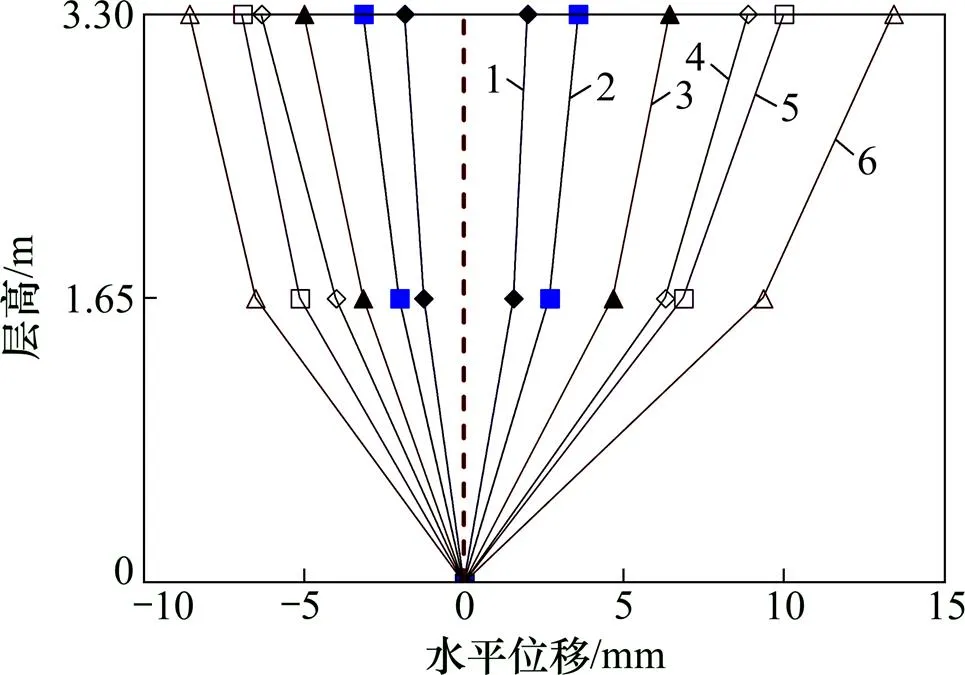
加速度峰值/(cm∙s−2)：1—100；2—200；3—400；4—600；5—800；6—1 000

2.4 荷载−位移滞回曲线

在不同峰值地震波作用下，框架模型所承受的底部总剪力−顶层位移滞回曲线如图7所示。由图7可见：滞回曲线近似呈线性分布，说明结构基本上处于弹性工作状态；同时，随着结构损伤的累积，在相同荷载作用下框架的顶点侧移有增加的趋势。

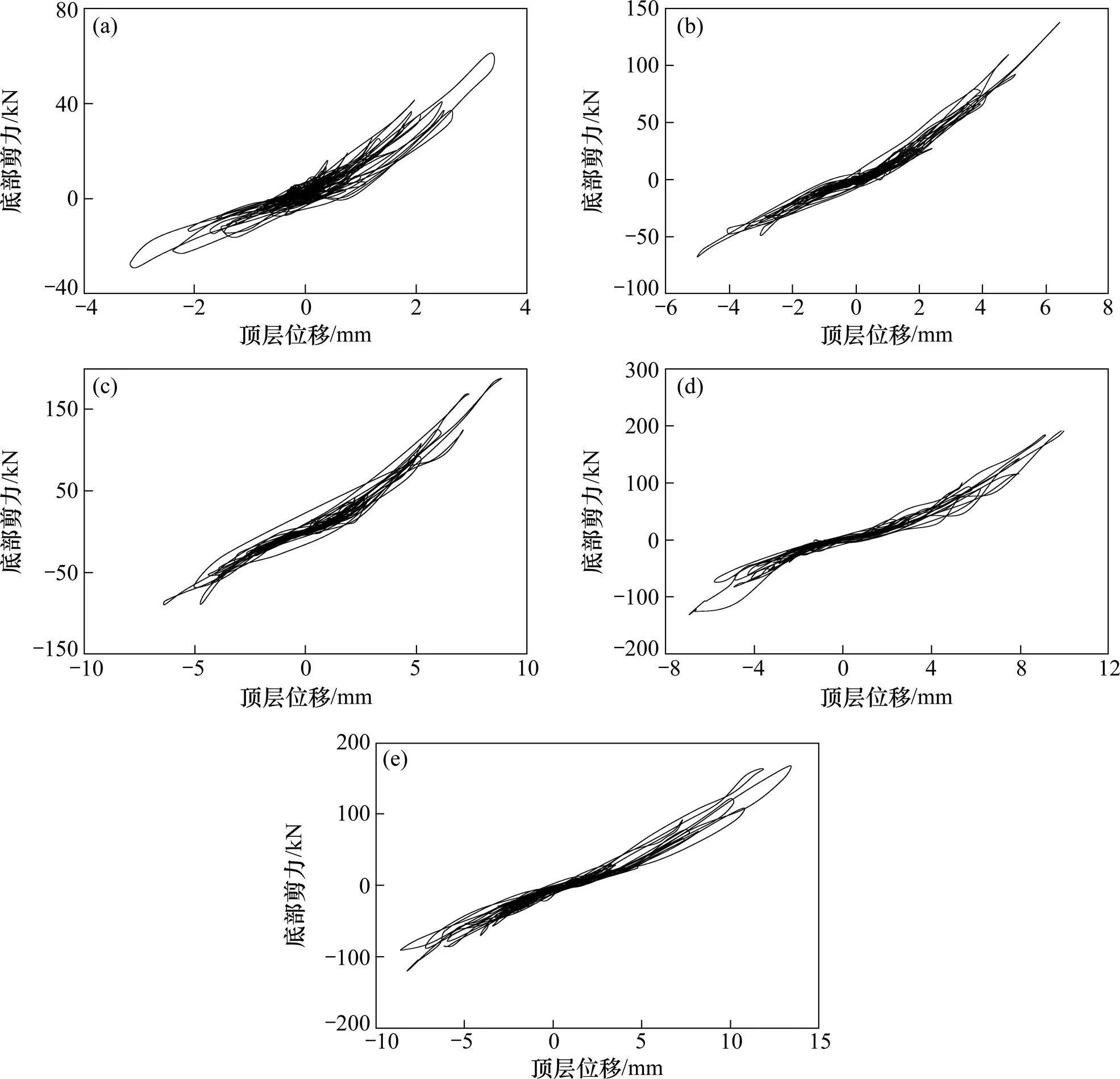
加速度峰值/(cm∙s−2)：(a) 200；(b) 400；(c) 600；(d) 800；(e) 1 000

2.5 刚度退化

地震作用下，损伤的累积将导致结构抗侧刚度的退化和自振频率的降低。在经历100，200和400 cm/s2地震波作用后，实测的层间抗侧刚度约为初始刚度的98.3%，96.2%和94.1%。在随后的加载过程中，实测的框架抗侧刚度变化不大。由此可知：在经历上述地震波作用后，结构的抗侧刚度最高降低了约6%。实测框架模型的基频变化如图8所示，图8中，f为经历相应峰值的地震波作用后结构的基频，0为结构的初始基频。由图8可知：试验结束时，结构的基频最多降低了约7%。刚度和基频变化不大说明框架的累积损伤较有限。

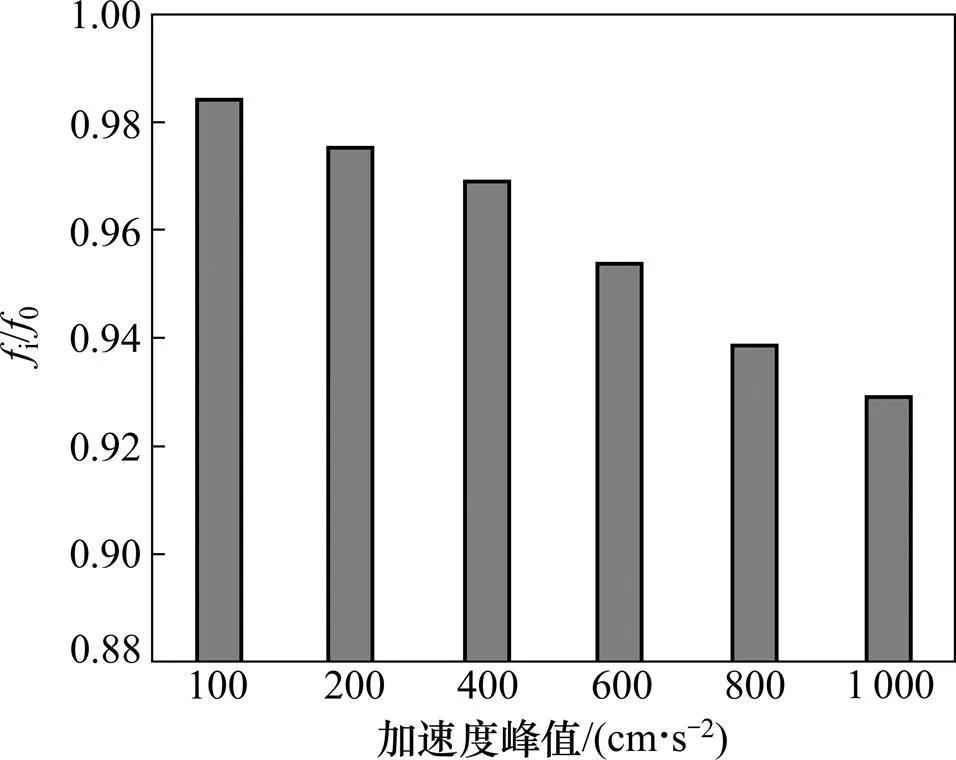
图8 基频柱状图

2.6 耗能特点

图9所示为结构的累积耗能曲线。由图9可见：累积耗能曲线呈台阶状分布。在1.0~2.0 s和3.1~3.5 s的2个时间段内耗能曲线有较明显的陡升段，上述时间段对应试验波最大峰值所处的区间。在其他时间段内，结构的耗能增加平稳。在累积耗能的陡升段，地震作用较为集中，结构中出现了一定的损伤，在宏观上表现为新裂缝出现、已有裂缝宽度增加、长度延长。结合荷载–顶点位移曲线以及结构抗侧刚度的退化程度可知，框架模型主要通过自身的弹性变形来消耗地震能量。

加速度峰值/(cm∙s−2)：1—100；2—200；3—400；4—600；5—800；6—1 000

3 抗震性能综合评估

由于试验中未在框架柱顶施加轴向压力，拟动力试验结果仅能反映原型结构顶部两层的地震响应。研究表明：在相当于9度及9度以上地震波的作用下，裂缝主要集中分布于框架梁端，梁柱核心区未发生破坏；在不同峰值地震波作用下，框架模型均处于弹性工作状态。在一般情况下，由于鞭端效应的影响，框架顶部结构的地震响应通常会增大。试验表明，SRC异形柱框架的顶部结构在高烈度地震作用下的损伤程度较小，并可满足规范对层间位移角的限值要求。

拟动力试验结束后，由于框架模型仍处于弹性状态，为了研究其在地震作用下的最终破坏形态，又对框架进行了拟静力试验。在拟静力试验中，采用了在顶层楼盖处施加单点低周反复水平荷载的加载方式，同时在每个框架柱顶施加1 000 kN的轴向压力。拟静力试验的主要试验结果见文献[20]，研究表明：SRC异形柱框架模型的耗能性能良好，塑性铰形成机制合理，结构的位移延性系数不小于3.0。

综合分析可知，SRC异形柱框架具有良好的抗震性能；通过合理设计，其具备应用于高烈度地震区的条件。

4 结论

1) 在拟动力试验中，在不同峰值地震波作用下，裂缝主要集中分布于框架梁端部；楼盖处的动力系数介于1.08~2.25之间；SRC异形柱框架层间位移角满足规范限值的要求。

2) 在经历了不同峰值地震波作用后，框架的抗侧刚度和基频分别下降了约6%和7%，这表明在高烈度地震作用下，结构尚处于弹性工作阶段，地震引起的结构累积损伤有限。

3) SRC异形柱框架具有良好的抗震性能，具备应用于高烈度地震区的条件。由于开展的试验数量有限，SRC异形柱中钢骨的合理配置以及梁柱构件的优化设计等内容有待进一步研究。

[1] 陈宗平, 张喜德, 苏益声, 等. 型钢混凝土异形柱正截面承载力的理论研究[J]. 西安建筑科技大学学报, 2005, 37(3): 345−349. CHEN Zongping, ZHANG Xide, SU Yisheng, et al. Theoretical research on bearing capacity of normal cross section of SRC special-shaped columns[J]. Journal of Xi'an University of Architecture & Technology, 2005, 37(3): 345−349.

[2] 蒋丽娜. 钢骨混凝土T形截面异形柱抗震性能试验研究[D]. 南宁: 广西大学土木建筑工程学院, 2006: 9−21.JIANG Lina. Experimental research on seismic behavior of steel reinforced concrete special-shaped column[D]. Nanning: Guangxi University. College of Civil Engineering and Architecture, 2006: 9−21.

[3] 邓志恒, 唐光暹, 向平, 等. 钢骨混凝土T形截面柱节点抗震性能研究[J]. 建筑结构, 2010, 40(6): 44−47.DENG Zhiheng, TANG Guangxian, XIANG Ping, et al. Experimental study on seismic behavior of SRC T−shaped column joints under low cyclic reversed loading[J]. Building Structure, 2010, 40(6): 44−47.

[4] 薛建阳, 王玮, 刘义, 等. 反复荷载作用下型钢混凝土异形柱框架边节点力学性能试验研究[J]. 西安建筑科技大学学报, 2011, 43(3): 323−329. XUE Jianyang, WANG Wei, LIU Yi, et al. Study on mechanical behaviors of steel reinforced concrete T-shaped column-beam joints[J]. Journal of Xi'an University of Architecture & Technology, 2011, 43(3): 323−329.

[5] 薛建阳, 刘祖强, 葛鸿鹏, 等. 实腹式型钢混凝土异形柱中框架抗震性能试验研究[J]. 建筑结构学报, 2011, 32(11): 82−88. XUE Jianyang, LIU Zuqiang, GE Hongpeng, et al. Seismic behavior of solid steel reinforced concrete middle frame with special-shaped columns[J]. Journal of Building Structures, 2011, 32(11): 82−88.

[6] 薛建阳, 高亮, 刘祖强, 等. 空腹式型钢混凝土异形柱中框架拟静力试验及有限元分析[J]. 建筑结构学报, 2012, 33(8): 31−40. XUE Jianyang, GAO Liang, LIU Zuqiang, et al. Quasi-static test and finite element analysis on lattice steel reinforced concrete middle frame with special-shaped columns[J]. Journal of Building Structures, 2012, 33(8): 31−40.

[7] 刘祖强, 薛建阳, 倪茂明, 等. 实腹式型钢混凝土异形柱边框架拟静力试验及有限元分析[J]. 建筑结构学报, 2012, 33(8): 23−30. LIU Zuqiang, XUE Jianyang, NI Maoming, et al. Quasi-static test and finite element analysis on solid-web steel reinforced concrete exterior frame with special-shaped columns[J]. Journal of Building Structures, 2012, 33(8): 23−30.

[8] 杨远龙, 杨华, 张素梅. 内置格构式圆钢管的T形型钢混凝土柱力学性能试验研究[J]. 工程力学, 2013, 30(3): 355−364.

YANG Yuanlong, YANG Hua, ZHANG Sumei. Experimental research on mechanical behavior of latticed circular tubes reinforced concrete T-shaped columns[J]. Engineering Mechanics, 2013, 30(3): 355−364.

[9] 方林, 张波, 金国芳, 等. 型钢混凝土十字形异形柱抗震性能试验及有限元分析[J]. 中南大学学报(自然科学版), 2015, 46(3): 1027−1033.

FANG Lin, ZHANG Bo, JIN Guofang, et al. Experimental study and finite element analysis on seismic behavior of steel reinforced concrete cross-shaped columns[J]. Journal of Central South University (Science and Technology), 2015, 46(3): 1027−1033.

[10] 薛建阳, 薛皓, 刘祖强. 型钢混凝土异形柱滞回性能分析[J]. 西安建筑科技大学学报, 2014, 46(6): 780−784.

XUE Jianyang, XUE Hao, LIU Zuqiang. Analysis on hysteretic behavior of steel reinforced concrete special-shaped column[J]. Journal of Xi'an University of Architecture & Technology, 2014, 46(6): 780−784.

[11] 李磊, 郑山锁, 张传超, 等. 型钢高强高性能混凝土框架拟动力试验研究[J]. 建筑结构, 2012, 42(3): 84−90. LI Lei, ZHENG Shansuo, ZHANG Chuanchao, et al. Pseudo-dynamic test on steel reinforced high strength and high performance concrete frame[J]. Building Structure, 2012, 42(3): 84−90.

[12] 陈鑫, 阎石, 季保建. 高强钢筋高强混凝土框架结构拟动力试验研究[J]. 大连理工大学学报, 2012, 52(5): 689−695. CHEN Xin, YAN Shi, JI Baojian. Pseudo-dynamic experimental research on high-strengthen concrete frame structure reinforced with high-strength rebars[J]. Journal of Dalian University of Technology, 2012, 52(5): 689−695.

[13] 宗周红, 夏坚, 林锦滔, 等. 两层预制板砖砌体结构房屋模型双向拟动力试验研究[J]. 建筑结构学报, 2012, 33(11): 62−71. ZONG Zhouhong, XIA Jian, LIN Jintao, et al. Bi-directional pseudo-dynamic test of a scaled two-story brick masonry building model with precast floor slabs[J]. Journal of Building Structures, 2012, 33(11): 62−71.

[14] 宗周红, 林东欣, 房贞政, 等. 两层钢管混凝土组合框架结构抗震性能试验研究[J]. 建筑结构学报, 2002, 23(2): 27−35. ZONG Zhouhong, LIN Dongxin, FANG Zhenzheng, et al. Experimental research on seismic behavior of a two-storey concrete filled steel tubular composite frame[J]. Journal of Building Structures, 2002, 23(2): 27−35.

[15] 王成刚, 胡波, 柳炳康, 等. 再生混凝土框架拟动力试验研究和分析[J]. 工业建筑，2013, 43(10): 50−54, 90.

WANG Chenggang, HU Bo, LIU Bingkang, et al. Pseudo-dynamic experimental and analytical study of two-story recycled aggregate concrete frame[J]. Industrial Construction, 2013, 43(10): 50−54, 90.

[16] 王焕, 宋满荣, 柳炳康. 单跨3层预压装配式预应力混凝土框架拟动力分析[J]. 合肥工业大学学报, 2012, 35(7): 947−950.

WANG Huan, SONG Manrong, LIU Bingkang. Pseudo-dynamic analysis of three-story one-span post-tensioned precast prestressed concrete frame[J]. Journal of Hefei University of Technology, 2012, 35(7): 947−950.

[17] GB50011—2010, 建筑抗震设计规范[S]. GB50011—2010, Code for seismic design of buildings [S].

[18] 邱法维, 钱嫁茹, 陈志鹏. 结构抗震实验方法[M]. 北京: 科学出版社, 2000: 95−99.

QIU Fawei, QIAN Jiaru, CHEN Zhipeng. Experimental methods for earthquake resistance of structures[M]. Beijing: Science Press, 2000: 95−99.

[19] JGJ 149—2006, 混凝土异形柱结构技术规程[S]. JGJ 149—2006, Technical specification for concrete structures with specially shaped columns[S].

[20] 杨涛, 张喜德. T形截面钢骨混凝土异形柱框架抗震性能[J]. 土木建筑与环境工程, 2009, 31(2): 33−37. YANG Tao, ZHANG Xide. Research on Seismic Behavior of Frame with T-shaped SRC Columns[J]. Journal of Civil, Architectural & Environmental Engineering, 2009, 31(2): 33−37.

(编辑 陈爱华)

Pseudo-dynamic Test on Seismic Behavior of Frame with T-shaped SRC Columns

YANG Tao, ZHANG Xide, ZHONG Hainiu, DENG Zhiheng

(Guangxi Key Laboratory of Disaster Prevention and Engineering Safety,College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China)

A half scale single-bay and two-story frame model was made, which was composed of reinforced concrete (RC) beams and T-shaped steel reinforced concrete (SRC) columns. The pseudo-dynamic test method was used to investigate seismic behaviors of the frame such as seismic responses and energy dissipation, and El centro earthquake waves with different peak acceleration were applied on the frame in the test. The experimental results indicate that structural damage due to earthquake is mainly located at the beam ends, and dynamic coefficients at the floors lie between 1.08 and 2.25. Additionalloy, the maximum inter-story drift angles of the frame meet the limitation requirement specified by Chinese codes. The lateral stiffness of the frame reduces by 6% after it is subjected to the earthquake wave with peak acceleration 1 000 cm/s2. Frames with SRC special-shaped columns possess good seismic performance and they are feasible to be applied in high intensity earthquake zone.

steel reinforced concrete (SRC); special-shaped column; frame; seismic behavior; pseudo-dynamic test

10.11817/j.issn.1672-7207.2015.06.027

TU398.2；TU317.1

A

1672−7207(2015)06−2171−07

2014−04−13；

2014−07−20

国家自然科学基金资助项目(51268005)；广西自然科学基金资助项目(2014GXNSFBA118258)(Project (51268005) supported by the National Natural Science Foundation of China; Project (2014GXNSFBA118258) supported by the Guangxi Natural Science Foundation)

杨涛，讲师，博士，从事混凝土结构与组合结构受力性能的研究；E-mail：yt48440002@163.com