常见的数学解题思想

杨英杰

（铜仁学院 数学科学学院，贵州 铜仁 554300 ）

常见的数学解题思想

杨英杰

（铜仁学院 数学科学学院，贵州 铜仁 554300 ）

常见的数学解题思想有四类：函数与方程、转化与化归、分类讨论、数形结合。本文讨论这四类数学解题思想在学习中的应用，从而引导学生学好数学。

函数与方程；化归；分类讨论；数形结合

“学好数理化，走遍天下都不怕”是上世纪 80年代非常响亮的一句口号，这也充分说明数理化在生活当中的重要意义。而数理化当中最难学好的是数学，很多学生，提到数学就头疼。那么该如何学好数学呢？要想学好数学，就要掌握数学解题思想，思想掌握了，学好数学自然就轻松多了。本文重点探讨四类常见的数学解题思想：函数与方程、转化与化归、分类讨论、数形结合，将这四类数学解题思想逐一阐述，并结合例题进行分析说明。

1.函数与方程

函数与方程的思想即是通过对问题中的各数量的依赖关系的分析，将问题定性为函数问题或方程问题，然后通过对函数或方程的讨论解决问题［1］。下面结合例题进行分析。

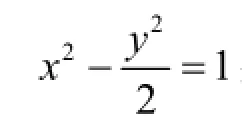
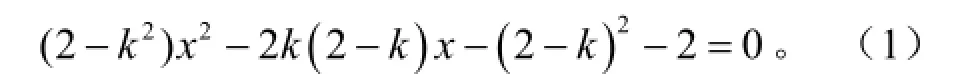
设A点坐标为（x1，y1）、B点坐标为（x2，y2），x1，x2为方程（1）的两根，那么（1）必为二次方程，所以2-k2≠0，且由韦达定理可知：

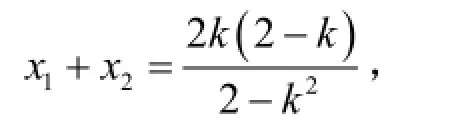
解得k=1，故直线AB的方程为：1yx=+。

本题是将所求量作为未知数置于相关量的依附中，从两个不同的方面去研究目标，建立等量关系，从而得到一个方程，进而通过解方程求得未知数的值，有一定的技巧。

2.转化与化归

转化与化归思想在于将未知的、繁杂的问题通过演绎归纳转化为已知的、相对较简单的问题，化繁为简，有利于求解［2］。常见的转化方法有：一般特殊化、等价转化、复杂简单化、变量代换等。下面结合例题进行分析。

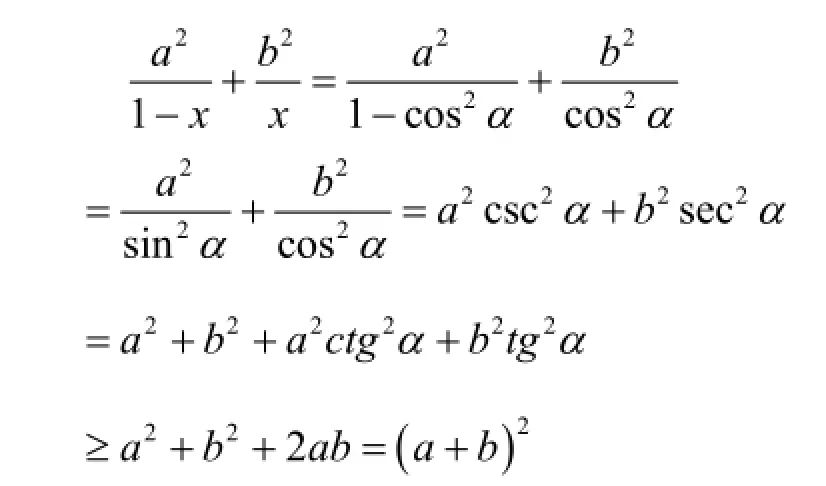
本题采用变量代换使得问题简化。在运用转化与化归的思想时，重点与难点是辅助函数的选择。辅助函数选择适当，问题就迎刃而解；反之，会使计算更加繁琐。所以选择时要慎重，有时候要反复尝试。

3.分类讨论

当一个问题因为某种相应的量或图形的情况不同而有可能导致问题的结论不同时，需要对这个相应的量或图形的各种情况进行分类讨论。分类讨论是一种重要的解题方法，常常能起到简化问题达成解决问题的作用。解题过程实质是一个变形过程，往往需要对问题做一些假设，从而引起分类讨论［3］。

例3 求函数y=（k+1）x2+x-k与x轴的交点坐标。

分析：本题的题设是不唯一的，这样的函数是什么函数？因此要进行分类讨论，一类是一次函数，一类是二次函数。

（1）如果k=-1，则函数为一次函数，那么它与x轴唯一交点为 （-1，0）；

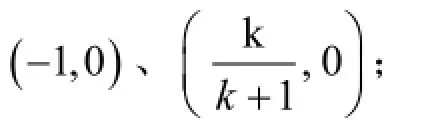
b. 当Δ=0，解得k=-1/2时，因此有一个交点，为（-1，0）；

综上所述，我们可知：

当k=-1时，与x轴交点为（-1，0）；

当k=-1/2时，与x轴只有一个交点，为（-1，0）。

由上面例子可知，对于分类讨论问题，审清题意是关键，如果不认真审题，往往会出现漏解或者重复求解的情况。因此在做此类型的题目时一定要审好题，考虑全面，把所有可能出现的情况一一罗列出来，分别讨论，这样才能做好此类问题。教师在讲解此类问题时，一定要求学生认真审题，拒绝粗心大意，考虑所有情况，从而有效解题。

4.数形结合

数形结合就是既分析数学问题的代数意义，又揭示其几何意义。几何图形更加直观，更好理解，有利于求解；反过来，图形的求解又依赖于代数来表述。因此，二者是相辅相成的关系［4］。

例4 如图1所示，在四边形ABCD中，ΔABD、ΔBCD 和 ΔABC的面积之比为3：4：1，点M、N分别在AC、CD上，且满足AM：AC=CN： CD，且B、M、N三点共线。求证：M与N分别是AC和CD的中点。

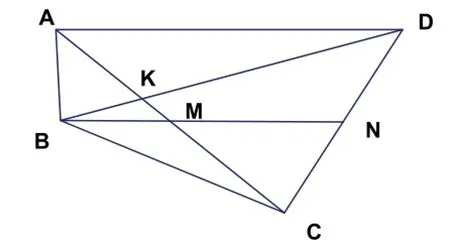
图1　例4示意图

证明：在 KDCΔ的三边（所在直线）CD、DK、KC被一直线分别截于点N、B、M，则由珻勒崂（Menelaus）定理可得，

由于AM：AC=CN： CD ，则可以假设

又由于 ABDΔ，BCDΔ和 ABCΔ的面积之比为3：4：1，则

所以

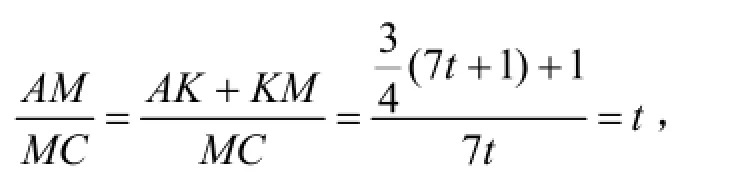
本题通过珻勒崂（Menelaus）定理把几何题转化为代数题，从而运用代数方法解决问题。

5.小结

本文探讨了常见的四类数学解题思想，并用例子加以说明，从中我们可以看出数学解题思想在学习中的应用的一个梗概。教师在数学教学中应将数学解题思想与整个基础知识的讲解、传授融为一体。“授人以鱼，不如授人以渔”，教师在教学中不但要注重传授学生数学基础知识，而且更重要的是注重传授学生数学解题思想。通过对习题的讲解使学生逐步掌握有关的数学解题思想，从而提高学生的数学能力，使学生养成良好的数学素质。在这一过程中，教师应提高自身的教学修养，提升教学理念，真正以“人”为本提高课堂效益与教学质量。

［1］张奠宙，宋乃庆.数学教育概论［M］.第二版.北京：高等教育出版社，2009.

［2］吕凤祥.中学数学解题方法［M］.哈尔滨：哈尔滨工业大学出版社，2003.

［3］华东师范大学数学系.数学分析［M］.北京：高等教育出版社，1991.

［4］张雄，李得虎.数学方法论与解题研究［M］.北京：高等教育出版社，2009.

On the Thinking of Solving the Mathematics Problems.

YANG Ying-jie
（School of Mathematics and Computer Science，Tongren University，Tongren，Guizhou 554300，China ）

Common mathematics problem-solving thoughts have four categories： function and equation，transformation and reduction，classification discussion，combination of number and shape. The paper discussed the four categories for application in study as to guide the students to learn mathematics well.

function and equations，transformation and reduction，classification discussion，combination of number and shape

G424

A

1673-9639 （2015） 04-0190-03

（责任编辑 毛志）（责任校对 徐松金）（英文编辑 田兴斌）

2014-04-17

本文系贵州省科技厅项目（黔科合J字LKT［2012］24号），铜仁学院自然科学基金（TS10018）研究成果。

杨英杰（1982-），女，副教授，硕士，主要研究方向：最优化方法、生物信息学、控制论。