基于MATLAB的设施选址0-1规划的实现
2015-10-11姚益新
姚益新
(华北电力大学,北京 102206)
基于MATLAB的设施选址0-1规划的实现
姚益新
(华北电力大学,北京 102206)
设施选址问题由于涉及的因素纷繁复杂,造成其求解的难度也一直很大。针对这个问题,本文使用matlab软件对采用0-1规划的设施选址问题进行了解答,并进行了实例的论证,结果表明在使用matlab对0-1规划的设施选址问题进行解答时,具有调用函数简单,求解方便等优点。
设施选址;0-1规划;matlab
一、前言
选址作为企业活动中最重要的长期决策之一,选址的好坏将对服务方式、服务质量、服务效率、服务成本等造成直接的影响,进而影响到企业利润及其市场竞争力。而设施选址作为众多选址问题的一个重要研究领域,更是关系到经济、政治、文化、社会、生态等各个社会方面,是一项综合的系统工程,在当前将建设资源节约型、环境友好型社会作为加快转变经济发展方式的重要着力点的时代背景下,其研究无疑具有重大现实意义[1]。设施选址规划的研究方法主要依靠运筹学、拓扑学、管理学等计量方法,这是设施选址与其他选址问题的重要区别[2]。在选址问题的讨论时,涉及到从多个地址中选择适当的个数和地点进行选址的问题,此时通常采用0-1规划来实现[3]。
二、选址0-1规划模型
0-1规划是决策变量仅取值0或1的一种特殊的整数规划。0-1变量可以数量化地描述诸如开与关、取与弃、有与无等现象所反映的离散变量间的逻辑关系、顺序关系以及互斥的约束条件,因此0-1规划非常适合用来解决如线路设计、工厂选址、生产计划安排等人们所关心的多种问题[4]。
0-1规划的基本数学模型为
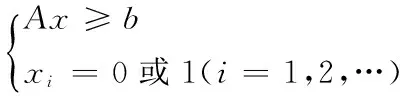
(1)
三、0-1规划的MATLAB实现
在MATLAB中由于自变量的取值非常有限,因此如果自变量个数不多的话,完全可用穷举法得到最优解。对于自变量个数比较多的情况,可以用隐枚举法求得最优解。与穷举法不同的是,隐枚举法只检查自变量取值组合的一部分,它通过找到的可行解不断改进目标值,于是它只检查优于目标值的取值组合,因此在应用隐枚举法之前必须先给一个可行解。
在MATLAB中编程实现的枚举法法函数为:ZeroOneprog。功能为用枚举法(包括穷举法和隐枚举法)求解0-1规划。其调用格式为:
[intx,intf]=ZeroOneprog(c,A,b,x0)
其中,c:目标函数系数向量;
A:不等式约束右端向量;
x0:初始可行整数解;
intx:目标函数取最小值时的自变量值;
intf:目标函数的最小值。
四、实例分析
某地政府决定计划投资5000万在某地区建立物流配送中心。已知该区域有15个社区,并有7个位置可以建设物流配送中心,但是每个配送中心只能覆盖有限个社区,且由于地理位置、气候以及交通等因素,每个可选位置建设物流配送中心的费用及覆盖范围也各有差异。社区分布及物流配送中心建设点的位置示意图如图1所示,每个位置建设物流配送中心的费用以及可以覆盖的社区如表1所示,每个社区的人口数如表2所示。
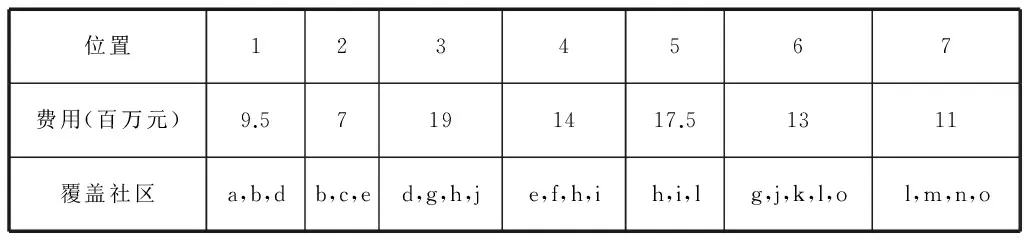
表1 各位置建设物流配送中心的费用及所能覆盖的社区

表2 各社区的人口数量
问题:要求在建设费用不超过5000万的前提条件下,在7个位置中选择合适的位置建立物流配送中心,使得使覆盖的人口尽可能的多;
(一)模型的假设。
假设一:各社区人口数量不发生变化;
假设二:各社区内居民对物流配送中心的使用率相同,均为α;
假设三:若某社区在某物流配送中心的覆盖范围之内,那么该社区中所有客户均被改物流配送中心覆盖;
假设四:各物流配送中心不会重复建设;
假设五:各物流配送中心的重复覆盖不对配送服务的质量造成影响;
(二)符号说明。
xi:各物流配送中心的建设情况(xi=1表示第i个物流中心需要建设,xi=0表示第i个物流中心无需建设);
a:物流配送中心使用率(0 M:物流配送中心的建设总成本; W:在某建设方案下,物流配送中心覆盖的等效人口。 (三)模型准备。 根据表1和表2中的信息,我们可以将所有社区对应的物流配送中心的位置情况统计如表3所示: 表3 各个社区对应的物流配送中心的位置情况 (四)建立模型。 对于该案例中的物流配送中心,只有建设和不建设这两种情况,因此,我们可以采用0-1规划的思想进行建模。设xi为每一个物流配送中心的建设情况,则有: 其中xi=1表示第i个物流配送中心需要建设,xi=0表示第i个物流配送中心不需要建设。同时需要考虑,同一个社区,有可能有多个物流配送中心覆盖,如果覆盖同一社区的物流配送中心都进行了建设之后,那么该社区的人口就会被重复计算。 本案例要求在建设费用不超过5000万的前提条件下物流配送中心覆盖的人口最大,那么我们可以根据表1和表2中的数据,将目标函数表述如下: maxW=2*x1+4*max{x1,x2}+13*x2+6max{x1,x3}9max{x2,x4}+4x4+7.5max{x3,x6}+12.5max{x3,x4,x5}+10max{x4,x5}11max{x3,x6}+6x6+14max{x5,x6,x7}+9x7+3.5x7+6max{x6,x7} (2) 约束条件为:建设物流配送中心的费用不超过5000万元的预算,表达式如下: 9.5x1+7x2+19x3+14x4+17.5x5+13x6+11x7≤50 (3) 考虑到物流配送中心需要建设与否,我们有 (4) 最终模型为 maxW=2*x1+4*max{x1,x2}+13*x2+6*max{x1,x3}+9*max{x2,x4}+4*x4+7.5*max{x3,x6}+12.5*max{x3,x4,x5}+10*max{x4,x5}+11*max{x3,x6}+6*x6+14*max{x5,x6,x7}+9*x7+3.5*x7+6*max{x6,x7} (5) (五)模型解答。 代入原模型,可将上述模型转换为: min=-2*x1-13*x2-4*x4-6*x6-12.5*x7-4*b1-6*b2-9*b3 -18.5*b4-12.5*b5-10*b6-14*b7-6*b8 在MATLAB中输入下列命令 >>c=[-2;-13;0;-4;0;-6;-12.5;-4;-6;-9;-18.5;-12.5;-10;-14;-6] >>A=[9.5 7 19 14 17.5 13 11 0 0 0 0 0 0 0;0.5 0.5 0 0 0 0 0-1 0 0 0 0 0 0 0;-1-1 0 0 0 0 0 1 0 0 0 0 0 0 0;0.5 0 0.5 0 0 0 0 0-1 0 0 0 0 0 0;-1 0-1 0 0 0 0 0 1 0 0 0 0 0 0;0 0.5 0 0.5 0 0 0 0 0-1 0 0 0 0 0;0-1 0-1 0 0 0 0 0 1 0 0 0 0 0;0 0 0.5 0 0 0.5 0 0 0 0-1 0 0 0 0;0 0-1 0 0-1 0 0 0 0 1 0 0 0 0;0 0 1/3 1/3 1/3 0 0 0 0 0 0-1 0 0 0;0 0-1-1-1 0 0 0 0 0 0 1 0 0 0;0 0 0 0.5 0.5 0 0 0 0 0 0 0-1 0 0;0 0 0-1-1 0 0 0 0 0 0 0 1 0 0;0 0 0 0 1/3 1/3 1/3 0 0 0 0 0 0-1 0;0 0 0 0 0 0.5 0.5 0 0 0 0 0 0 0-1;0 0 0 0 0-1-1 0 0 0 0 0 0 0 1] >>b=[50;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0];x0=[1;1;1;1;1;1;1;1;1;1;1;1;1;1;1] >>[intx,intf]=ZeroOneprog(c,A,b,x0) 所得结果为 intx=(0,1,0,1,0,1,1,1,0,1,1,1,1,1,1) 由计算结果可知,当选择在2,4,6,7号位置建设物流配送中心时,可以达到覆盖人口最多的目标。在这种方案下,建设物流配送中心总费用为7+14+13+11=45(百万元),覆盖2,3,5,6,7,8,9,10,11,12,13,14,15社区,总人口为109.5千人。 本文给出了物流规划与设计中的0-1整数规划模型,并通过使用MATLAB来求解。使用0-1整数规划模型能够很好的解决在数个备选地址间选择最优的选址地点的问题,优点是建模中做了适当的抽象化,将较为复杂的问题简化为数学模型,既找到合理解,又提高运算速度及效率,这对数据的分析是大有裨益的[5]。其具有较强的可操作性和一定的参考价值,得到的结果也较接近实际。缺点在于忽略了某些实际因素的影响,得到的结果与实际结果存在一定的偏差。另外MATLAB在目标函数中取最大值的问题时不能做出准确的阐述,这是一个缺憾。若要解决这个问题可用Linggo软件来求解,在同一社区,面对同时被多个物流配送中心覆盖,社区的人口就会被重复计算的问题我们可以用布尔代数的思想来避免这种情况。 [1]万波.公共服务设施选址问题研究[D].华中科技大学,2012. [2]刘海龙,李成严.物流中心选址方法研究[J].黑龙江科技信息.2010(4s):42-43 [3]丁小东,姚志刚,程高.LINGO语言与0-1混合整数规划选址模型的再结合[J].物流工程与管理.2009(10):72-75. [4]沈萍,陈燕,李捷,杨雪君.物流配送中心选址问题的0-1规划并行算法.计算技术与自动化[J].2012,09(3):80-82 [5]管志忠,吕楠.0-1线性规划模型的MATLAB实现及应用[J].徐州工程学院学报.2007(12):64-67 0221.1 A 1671-864X(2015)11-0197-02 姚益新(1989-),男,汉族,江苏常州,硕士研究生,华北电力大学,物流工程(物流与供应链管理)。
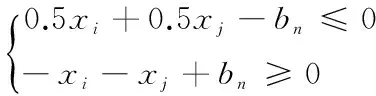
五、总结
