基于改进SIFT描述子的快速匹配算法*

钱冬云

（浙江工贸职业技术学院信息传媒学院，浙江温州325003）

基于改进SIFT描述子的快速匹配算法*

钱冬云

（浙江工贸职业技术学院信息传媒学院，浙江温州325003）

针对尺度不变特征变换（SIFT）算法中存在描述子维度高、特征点信息冗余和配准运算量大等问题，提出一种改进的ECF-SIFT（eightcircles features）算法。该算法通过高斯差分金字塔，确定特征点，并以环绕特征点的8个圆环为邻域构造64维的特征描述子，采用最近邻与次近邻之比对描述子进行匹配，最后用RANSAC算法对匹配点进行校正和消除误匹配。实验结果表明，在尺度缩放、尺度和旋转组合、视角变化、模糊变化和光照变化等条件下，ECF-SIFT算法的性能保持不变，并压缩了匹配时间，提高了匹配的准确率，算法的整体性能优于SIFT和SURF算法。

尺度不变特征变换；特征提取；特征描述子；RANSAC算法；图像配准；算法效率

0　引言

图像配准是计算机视觉和数字图像处理的重要组成部分。目前，图像配准已经被广泛应用于目标识别、目标跟踪、图像组合和三维重建等许多领域。图像配准的方法以灰度相关匹配和特征点的匹配两类为主。在灰度相关匹配方面，Moravec［1］提出角点特征，通过灰度自相关函数来考虑一个像素与其邻域像素的相似性，但是Moravec角点对图像间的亮度、尺度缩放等变化较为敏感，且计算复杂，不具备旋转不变性，抗噪声能力差等很多局限性［2］。目前大部分学者主要研究特征点的匹配算法。哥伦比亚大学的LOWEDG.［3］提出基于尺度不变特征的SIFT（scale invariant feature transform）算法。目前，SIFT算法被认为是最稳定的图像配准算法之一。SIFT算法使用128维的描述子，包含了丰富的信息量，使得SIFT算法对图像的旋转、尺度缩放和光照变化等都具有很好的鲁棒性。当图像尺寸较大，检测到特征点数目庞大时，使用128维的描述子，将出现配准计算时间长，占用系统资源过多，且实时性较差等问题。因此，很多学者在SIFT算法的基础上，提出了许多的改进算法。KE Y提出PCA-SIFT算法［4］，在归一化的梯度场中应用主成分分析（Principal Component Analysis，PCA）算法，将描述子进行降维处理，提高了算法的稳定性，但是实时性和鲁棒性有待提高；Bay［5］沿着LOWE的思路，提出了SUFT（Speeded-Up Robust Features）局部特征，SUFT描述子采用积分图像，在矩形区域内，利用Haar小波响应，来统计特征矢量，最终形成64维描述子，避免在特征矢量生成时对图像的重复计算，大幅度提高了匹配速度，但是其鲁棒性有待进一步提高；Mikolajczyk等［6］利用在环形区域内，利用对数极坐标同心圆GLOH（Gradient Location-Orientation Histogram），构建272维的特征矢量，然后采用PCA技术进行降维处理，降成128维，虽然提高算法的鲁棒性，但是计算复杂度大大提高，其运算效率较差；朱利成等［7］提出基于卡尔波曼滤波的改进的SIFT特征点匹配算法。由于卡尔波曼滤波的状态估算，造成运算效率低，实时性差。

针对SIFT算法的128维特征向量表示的计算的复杂缺陷，本文提出ECF-SIFT（eight circles features，ECF）算法，通过高斯差分金字塔，以近似R=3σ的半径，环绕特征点，划分8个同心圆，构成8个子环，然后计算每个子环内的各元素在8个方向的梯度值累加，构成64维的特征描述子，采用最近邻与次近邻之比来对64维描述子进行匹配，最后用RANSAC算法对匹配点进行校正和消除错误匹配。ECF-SIFT算法降低特征描述子的维度，降低特征点冗余和配准的计算复杂度，提高了配准的效率。

1　 SIFT算法

ECF-SIFT算法是一种基于SIFT算法的改进图像配准算法。由LOWED.G在1999年提出SIFT算法，并与2004年进行完善。SIFT算法是目前应用最广的特征检测图像匹配方法之一。SIFT算法主要包含几个步骤：（1）构建尺度空间；（2）确定关键点；（3）检测特征点；（4）描述特征点，构成特征向量；（5）匹配特征向量。

1.1构建尺度空间

一幅二维图像的尺度空间L（x，y，σ）函数表示，如式（1）所示，由不变尺度的高斯函数G（x，y，σ）与图像的I（x，y）卷积产生的函数表示。

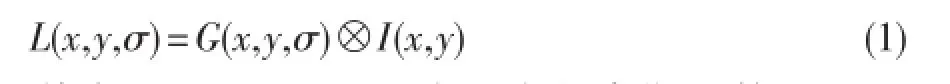
其中，G（x，y，σ）是尺度可变的高斯函数；I（x，y）表示为输入图像，表示在x和y方向上进行卷积操作；σ为尺度因子；G（x，y，σ）的值如式（2）。

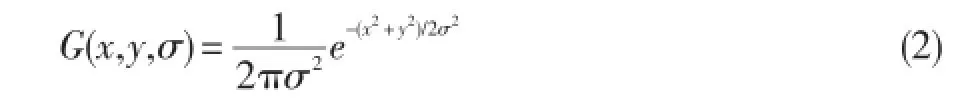
LOWE还给出了各尺度空间的σ的变化值，如式（3）。

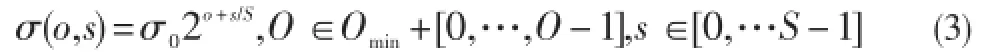
其中，σ∈R+，o∈Z，s∈N。σ0是基准层尺度，o为组（Octave）的坐标，s为层（Level）坐标。

对于特征点的检测，主要通过所在尺度空间所相邻的两个高斯尺度空间上的图像相减，然后得到一个DoG（Difference of Gaussions）的响应值图像D（x，y，σ）。

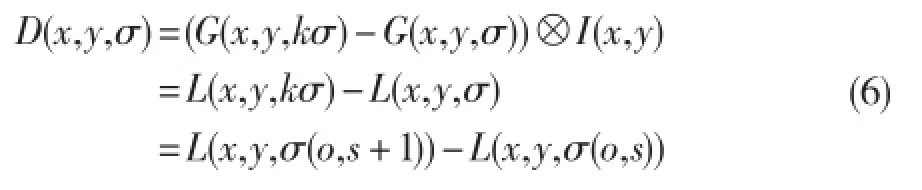
其中，k为相邻尺度空间倍数，如图1所示。

图1　高斯差分金字塔的生成

1.2关键点提取

关键点是由DoG空间的局部极值点。在同一组内，通过与DoG相邻两层的图像之间进行比较，得到初步的关键点，如图2所示。对于每个检测点，要与同尺度的围绕检测点的8个相邻点比较，还需与上下相邻尺度对应的9个点相比较，即与（8+9*2）共26个点比较，所以保证在尺度空间和二维的图像空间都检测到极值点。

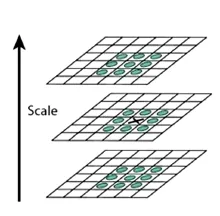
图2　DoG空间极值检测

1.3特征点检测

特征点检测主要目的要剔除低对比度点和不稳定的边缘相应点，以增强匹配的稳定性。利用三维二次函数拟合，确定关键点的位置和尺度，同时去掉对比度低的关键点和不稳定的边缘点。对空间尺度函数（7）求导，并令其为0，得到精确的位置Xˆ如式（8）和（9）。

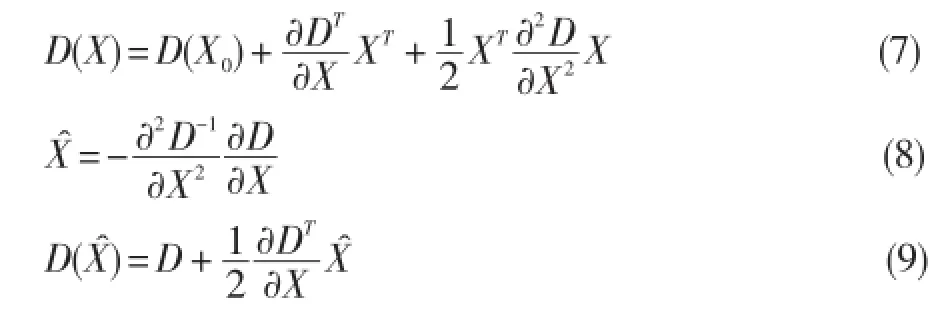
在高斯空间中设定阈值去除对比度低的关键点，若|D（Xˆ）|≥0.03，则该保留特征点，否则剔除。由于运算DoG算子会产生较强的边缘响应，对于不稳定的边缘点，可依据高斯差分算子的极值理论。一个横跨边缘的高斯差分算子有较大的主曲率，而垂直边缘方向的高斯差分算子有较小的主曲率。主曲率通过一个2×2的Hessian矩阵求出，如式（10）所示。

其中，X的值（x，y，σ）T包含特征点的位置和尺度信息的向量。由于D的主曲率和Hessian矩阵H的特征值成正比，所以可将式简化成为判断不等式。其中，令α为最大特征值，β为最小特征值，则：

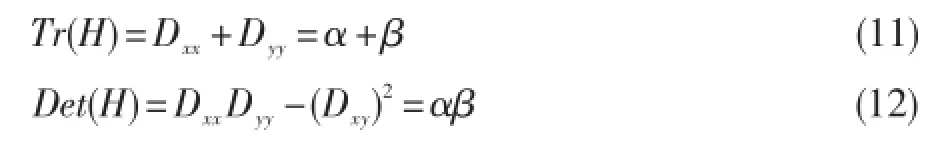
令α=γβ，则：

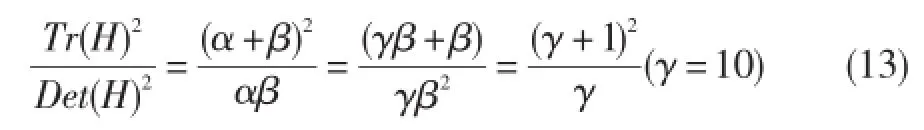
若式（14）成立，判断为边缘关键点，需剔除。

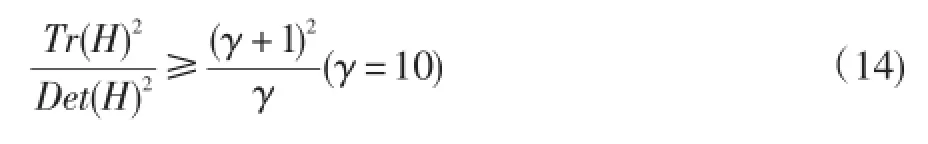
1.4特征点描述

1.4.1确定特征点的主方向

使用有限差分法，以关键点为中心，用radius为半径的邻域像素的梯度方向分为每个关键点的特征方向信息，梯度值m（x，y）和梯度方向（x，y），计算表达式分别为式（15）和式（16）。

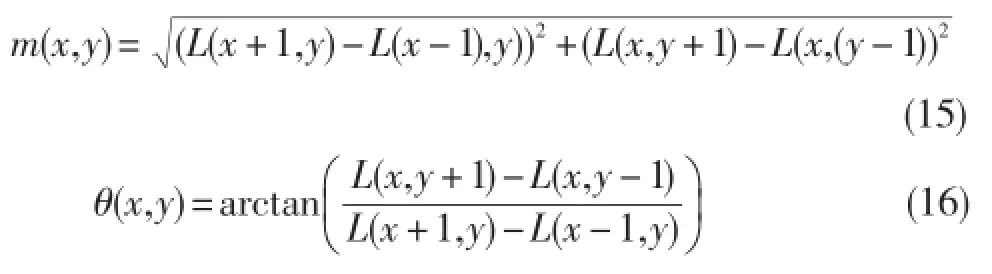
通过直方图统计关键点的邻域像素梯度方向。将直方图中的峰值表示该关键点的方向。

1.4.2特征点描述

以特征点为中心取8×8邻域为采样窗口来描述特征点。计算各块内的梯度直方图，生成向量描述符。在4×4为采样窗口的邻域内，计算每个领域的8个方向的梯度方向直方图，然后累加每个梯度方向值，形成一个种子点，每个特征点就用4×4×8= 128维向量来表征，最后对特征向量归一化消除光照的影响。

2　 ECF-SIFT算法的64维描述子的生成

ECF-SIFT算法在SIFT算法的基础改进特征点的描述子生成方式，采用64维描述子描述特征点；在特征点匹配时，增加使用RANSAC算法消除误匹配点，提高配准率。

由于圆环具有旋转不变特性，因此ECF-SIFT算法利用圆环作为邻域来构建描述子，虽然省略了旋转处理步骤，但自动具有旋转不变特征。LOWE认为在实际应用中，采用3σ为半径的邻域的综合效果最佳［1］，所以，ECF-SIFT算法采用与SIFT算法相同的邻域进行采样。以特征点为中心，以radius为半径，由式（17）得到，分别画出8个同心圆，如图3所示。在图中以不同的颜色表示最里层圆和7个圆环，将邻域划分为8个子域，使得特征描述子具有旋转不变特性。

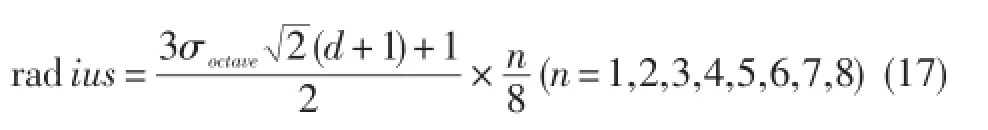
其中，σoctave为特征点所在的组内尺度。其中，当n的值取1，绘制第1个圆；当n的值取2，绘制第2个圆；以此类推，构建8个同心圆，得到1个圆V［1］和7个圆环V［i］（i=2，3，4，5，5，6，7，8）来表达。

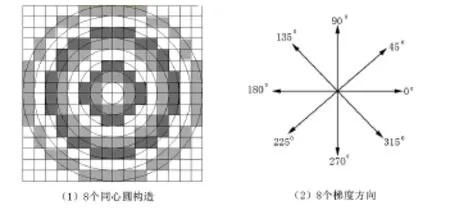
图3　ECF-SIFT算法的特征描述子的示意图

设特征点（x，y）在V［i］（i=1，2，3，4，5，6，7，8）子区域内中像素点的个数为nrρ，然后统计在每个子环内，对每个像素点在8个梯度方向的直方图定义为式（18），计算其梯度值和梯度方向，然后对每个梯度幅值乘以权重参数，生成直方图。

权重weight的计算如式（19）。

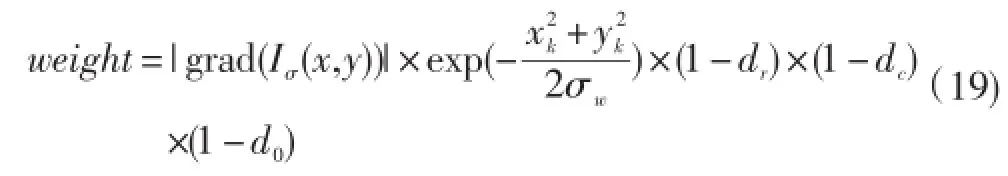
其中，xk和yk分别表示该像素点与特征点的列距离和行距离。

由式（18），按照i=1，2，3，4，5，6，7，8的顺序，计算所有子域V［i］对于的统计直方图组成一个特征向量Hi，其中的，同时将特征向量进行归一化处理，使得特征描述子对图像光照保持不变的特征，将特征向量组合（8×8）在一起构成特征描述子64维的描述子。

3　 ECF-SIFT特征点匹配

在匹配阶段，对两幅图像中同一特征点的对应位置进行匹配。本文采用欧式距离作为相似性度量函数，即根据最近邻域（Nearest Neighbor，NN）法来确定两个相匹配的特征点，选择可靠性高的匹配点对计算几何约束模型，进行精确匹配。由于旋转、光照、图像缩放和尺度变化等因素的影响，仍会存在部分的误匹配点，所以利用RANSAC算法消除误匹配。

Fischler和Bolles最先提出RANSAC（Random Sample Consensus）算法［8］。RANSAC算法中根据一组包含异常数据Outliers（偏离正常范围较远、无法适应数学模型的数据）的样本数据集，计算出数据的数据模型参数，得到有效的样本数据Inliers（可被模型描述的数据）的算法。本文使用RANSAC算法的基本思想描述如下。

（1）考虑一个最小的势为n抽样集模型和一个样本集P。集合P的样本数要求#（P）＞n。从匹配得到的结果集为样本数据集P，从P中随机选取4（n的值取4）对特征匹配对，构成P的一个子集S，由式（20）和（21）得到相应的变化模型参数矩阵H。

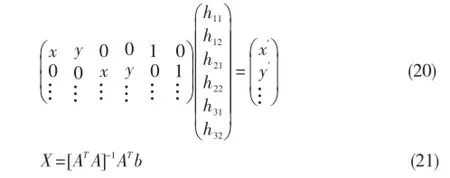
（2）计算剩余的特征点（P-4）对，经过变化矩阵的坐标值与它的匹配点之间的距离。

若小于设定的阈值T，则认为是内点，否则为外点。

（3）内点构成的集合S’为S的一致集。若一致集S中匹配点数目大于4，则使用最小二乘法重新计算新的模型H’，重新抽取4组，重复（1）到（3）步骤。

（4）在完成指定的抽取次数后，如果查找一致集算法失效，则选取在抽取后得到的最大一致集内判断内外点，最后算法结束得到最终结果。

4　实验与结果分析

为了验证ECF-SIFT算法使用描述子的有效性，将ECF-SIFT算法与传统的SIFT算法、SURF算法性能对比实验。实验仿真平台的硬件环境为：Intel（R）Core（TM）i5-337U CPU@1.80GHz，内存为4.0GB；软件Windows7操作系统，实验所采用的图片来自Mikolajczyk05标准数据集（http://www.robots.ox.ac.uk/～vgg/research/affine/）及实拍图像。

实验采用图像数据如图4到图8的5组图像所示。其中，图4为一组尺度缩放图，左侧的图片大小为384×256，右侧的图片大小为320×213；图5为一组尺度和旋转组合图片，图片大小均为850× 680；图6为一组视角变化图片，左侧的图片为1000×700，右侧的图片大小为880×680；图7为模糊变化的图片，图片大小均为1000×700；图8为一组光照变化图片，图片大小均为900×600。ECF-SIFT算法实验匹配效果如图4-图8所示，从图中可以看出ECF-SIFT算法在尺度缩放、尺度和旋转组合、视角变化和模糊变化和光照变化等都有较好的配准效果。

图4　尺度缩放

图5　尺度和旋转组合

图6　视角变化

图7　模糊变化

图8　光照变化

现采用平均匹配时间和平均匹配准确率来验证算法性能，图9和图10所示为性能实验的结果。对于时间曲线图来说，曲线与坐标轴之间的面积应当越小，效果越理想。从图9看出，ECF-SIFT算法在配准平均时间与SIFT算法相比约提升了75%左右；ECF-SIFT算法与SURF算法相比提升约45%。由于ECF-SIFT算法采用64维描述子，降低描述子生成的复杂度和冗余性，减少特征点的数目，缩短特征点配准的时间，实现了整体算法的快速匹配。匹配准确率的定义为正确匹配点数与所有匹配数之比。对于匹配准确率曲线图来说，曲线与坐标轴之间的面积应当越大，效果越理想。由图10得ECF-SIFT算法匹配准确性超过SIFT算法和SURF算法。从总体曲线构成的面积，ECF-SIFT算法与SIFT算法的准确率在同一级别上。由于SIFT算法采用128维描述子，而ECF-SIFT算法采用64维描述子。SIFT算法描述子包含大量冗余信息，虽然匹配正确率略有提升，但是匹配计算时间过长。从总体而言，ECF-SIFT算法超过传统的SIFT算法和SURF算法。

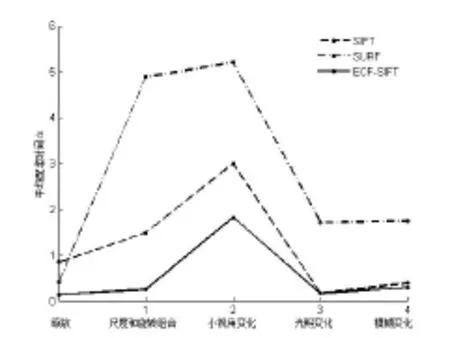
图9　平均匹配时间对比

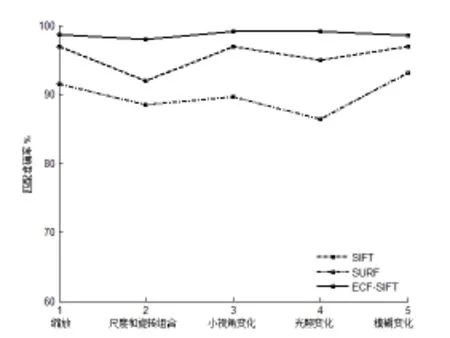
图10　平均匹配准确率对比

5　结束语

本文提出的ECF-SIFT算法降低描述子的生成复杂度，提高了算法的稳定性；并对特征向量进行归一化处理，消除光照的敏感性；使用RANSAC算法消除误匹配点，提高了配准的准确率，增强算法的鲁棒性。实验结果表明，ECF-SIFT算法对图像处理的旋转、尺度缩放、光照、模糊、视角变化具有很强的鲁棒性，并且提高了图像配准的准确度、快速性。因此，ECF-SIFT算法能广泛地应用在模式匹配领域。

［1］Moravec H P.TOWARDSAUTOMATIC VISUAL BBSTACLE AVOIDANCE［C］//International Conference on Artificial Intelligence（5th:1977:Massachusetts InstituteofTechnology）.1977.

［2］毕国玲，赵建，续志军，等.基于角点和局部特征描述子的快速匹配算法［J］.光电工程，2014，41（9）:63-68.

［3］Lowe D G.Object recognition from local scale-invariant features［C］//Computer vision，1999.The proceedingsof the seventh IEEE international conferenceon.Ieee，1999，2:1150-1157.

［4］Lowe DG.Distinctive image features from scale-invariantkeypoints［J］.International journalof computer vision，2004，60（2）:91-110.

［5］Ke Y，Sukthankar R.PCA-SIFT:Amore distinctive representation for local image descriptors［C］//Computer Vision and Pattern Recognition，2004.CVPR 2004.Proceedingsof the2004 IEEEComputer Society Conferenceon.IEEE，2004，2:II-506-II-513 Vol.2.

［6］Bay H，Tuytelaars T，Van Gool L.Surf:Speeded up robust features［M］//Computer Vision-ECCV 2006.Springer Berlin Heidelberg，2006:404-417.

［7］Mikolajczyk K，Schmid C.An affine invariant interest point detector［M］//Computer Vision—ECCV 2002.Springer Berlin Heidelberg，2002:128-142.

［8］朱利成，姚明海.基于SIFT算法的目标匹配和识别［J］.机电工程，2009，26（12）:73-74.

［9］Fischler M A，Bolles R C.Random sample consensus:a paradigm formodel fitting with applications to image analysis and automated cartography［J］.Communicationsof the ACM，1981，24（6）:381-395.

［10］常青，张斌，邵金玲.基于SIFT和RANSAC的特征图像匹配方法［J］.华东理工大学学报:自然科学版，2012，38（6）:747-751.

［11］刘辉，申海龙.一种基于改进SIFT算法的图像配准方法［J］.微电子学与计算机，2014（01）:38-42.

［12］牛俊伟，郝向阳，刘松林.一种改进的SIFT特征提取算法［J］.测绘科学技术学报，2014（02）:173-176.

（责任编辑：潘修强）

A FastMatching Algorithm Based on Im proved SIFT Feature Descriptor

QIAN Dong-yun
（Collegeof Information and Communications，Zhejiang Industry&Trade VocationalCollege，Wenzhou，325003，China）

An eight-circle-feature based scale invariant feature transform（ECF-SIFT）algorithm was developed to hurdle the problemsof the redundant feature point，large computation，and thehigh dimensionality of the scale invariant feature transform（SIFT）algorithm.The feature pointswere firstly determ ined by the difference of Gaussian.By utilizing eight concentric circlesaround the feature points，the 64-dimensional feature descriptors were created.The ratio of the first and the second closest distance was used to match the 64-dimesional vectors.Finally，thematching pointswere corrected by the RANSAC method to further remove the false matching.The ECF-SIFT algorithm demonstrated the invariance ofmatching performance for rotation，scale scaling，the changes of illum ination changes and smaller viewpoint，aswell as the blur，which is superior to the SIFT algorithm and SURF algorithm w ith the higherefficiency and betteraccuracy in imagematching.

scale invariant feature transform；feature extraction；feature descriptor；RANSAC algorithm；imagesmatching；algorithm efficiency

TP391.41

A

1672-0105（2015）03-0051-06

10.3969/j.issn.1672-0105.2015.03.012

2015-02-27

2014年度浙江省高等学校访问学者教师专业发展项目（FX2014177）；2014年度全国教育信息技术研究规划项目（146231964）；2014年度温州市科技计划项目（R20140090）

钱冬云，硕士，浙江工贸职业技术学院副教授，主要研究方向：图像分析、模式识别。