基于Bootstrap的加权FCM改进算法*

洪年松，范　渊，郭华峰

（浙江工贸职业技术学院信息传媒学院，浙江温州325003）

基于Bootstrap的加权FCM改进算法*

洪年松，范渊，郭华峰

（浙江工贸职业技术学院信息传媒学院，浙江温州325003）

为了提高模糊C-均值聚类算法的收敛速度，Yang等引入截断因子，提出了截断阈值模糊C-均值（FCMα）聚类算法，加快了算法的收敛。然而该算法也存在着聚类效果不佳的问题。针对该问题，使用Bootstrap统计方法进行特征加权，提出了基于Bootstrap的加权模糊C-均值聚类改进算法。实验表明，该算法具有更高的聚类准确率，也更有效。

FCM；截断阈值；Bootstrap；特征加权

0　引言

为了改善模糊C-均值（FCM）聚类算法的聚类效果，学者做了多方面的研究，包括特征加权和样本加权等几个方面。特征加权方面，袁正午等通过ReliefF算法实现特征权值的自动确定，提出了一种特征加权自适应FCM算法［1］，提高了算法的聚类精度。蔡静颖等则引入自适应马氏距离对特征加权进行处理，提出了一种基于马氏距离特征加权的模糊聚类算法［2］，提升了分类的有效性。样本加权方面，刘兵等提出了一种基于样本加权的可能性模糊聚类算法［3］，该算法具有更快的收敛速度和更强的鲁棒性。段林珊等则受热力学中熵定义的启发，提出了一种基于模拟退火的样本加权FCM算法［4］，提高了分类的准确数和准确率。与FCM算法类似，FCM的改进算法——FCMα算法［5］也存在着聚类效果不佳的问题。为了解决这个问题，本文将引入Bootstrap统计方法，对数据进行特征加权，改善FCMα算法的收敛效果。

1　截断阈值模糊C-均值聚类算法

为了改善FCM算法收敛速度慢的问题，YANG等引入截断因子，提出了截断阈值模糊C-均值（FCMα）聚类算法［5］，加快了算法的收敛。FCMα算法步骤如下：

①设定模糊指数1＜m＜∞，分类数2≤c≤n，迭代次数l=0，迭代终止阈值ε＞0，截断阈值0.5≤α≤1，初始化中心点起始值Z（0）。

②根据公式（1）计算隶属值μij。

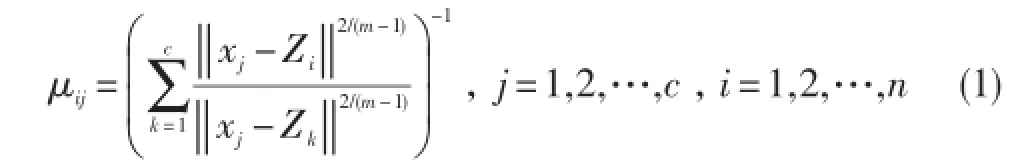
③使用以下方法更新μij，i=1，...，n，j=1，...，c：如果μis=max1≤j≤cμij＞α，那么μis=1，μis'=0，s'≠s。

④根据公式（2）计算中心点Z（l+1）。

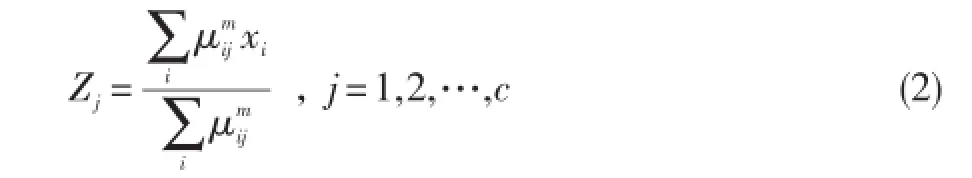
否则l=l+1，并回到步骤②。

FCMα算法虽然收敛速度得到了提升，但其聚类效果仍有改善的空间，下面将在该算法中引入Bootstrap特征加权方法。

2　截断阈值FCM算法的特征加权

2.1基于Bootstrap的特征加权方法

Bootstrap统计方法是现代统计学较为流行的一种统计方法，在小样本统计时效果很好。Bootstrap方法由B.Efron提出［6］，其主要思想是从原始数据中重复抽样以帮助我们认识样本特征，从而进一步认识母体特征。其基本步骤为：①采用重复抽样技术从原始样本中抽取给定数量的样本。②根据抽出的样本计算给定的统计量T。③重复上述B次，得到B个统计量T。④计算上述B个统计量T的样本方差。

根据Bootstrap方法的以上特点，FCMα算法所处理的数据样本可以使用该方法来计算特征权重，其计算步骤设计如下：

①给定重复抽样次数B，使用重复抽样技术从样本X=（x1，x2，…，xn）⊂RP中进行B次有放回的重复抽样，得到样本，，i=1，2，…，n，b=1，2，…，B，其中P为样本维数。

②使用公式（3）计算各次重复抽样的特征权重：

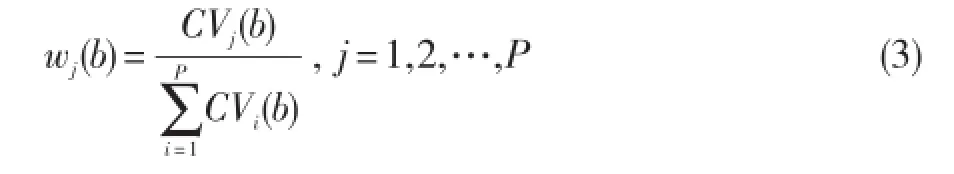
③使用公式（4）计算样本最终的特征权重：

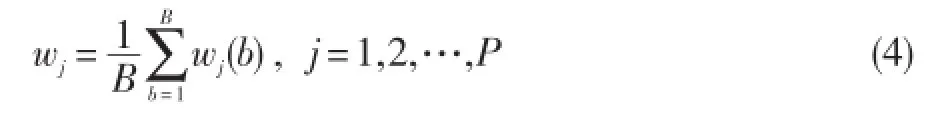
2.2基于Bootstrap的特征加权FCM改进算法

其中wk表示样本在第k个特征的加权，k=1，2，…，P。使用新距离对FCMα算法进行推算，就可以得到新的特征加权FCMα（简称WFCMα）算法，其迭代方程更新如下：

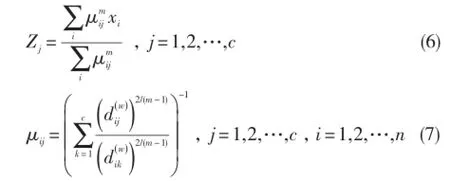
则新提出的WFCMα算法步骤如下：

①使用基于Bootstrap的特征加权方法计算样本特征权重。

②设定模糊指数1＜m＜∞，分类数2≤c≤n，迭代次数l=0，迭代终止阈值ε＞0，截断阈值0.5≤α≤1，初始化中心点起始值Z（0）。

③根据公式（7）计算隶属值μij。

④使用以下方法更新μij，i=1，...，n，j=1，...，c：如果μis=max1≤j≤cμij＞α，那么μis=1，μis'=0，s'≠s。

⑤根据公式（6）计算中心点Z（l+1）。

否则l=l+1，并回到步骤③。

观察算法可以发现，与FCMα算法相比，WFCMα算法多了第一步，即特征权重的计算，以及特征权重到算法的代入。为了验证WFCMα算法的效果，进行如下实验。

3　仿真实验

3.1数据集

采用正态分布的二维人工数据集和真实的高维数据集来验证算法的有效性。其中二维人工数据集有两个。第一个数据集分别以（3，4）、（7，4）为期望，单位矩阵I2为协方差矩阵。随机生成2堆正态分布的数据点，每堆100个数据，共200个数据点，如图1所示。第二个数据集分别以（3，4）为期望，单位矩阵I2为协方差矩阵，（7，4）为期望，矩阵为协方差矩阵。随机生成2堆正态分布的数据点，每堆100个数据，共200个数据点，如图2所示。真实的高维数据集则采用经典的Iris数据集［7］。

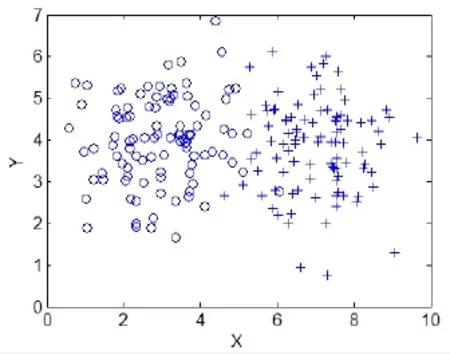
图1　随机生成的正态分布数据集1

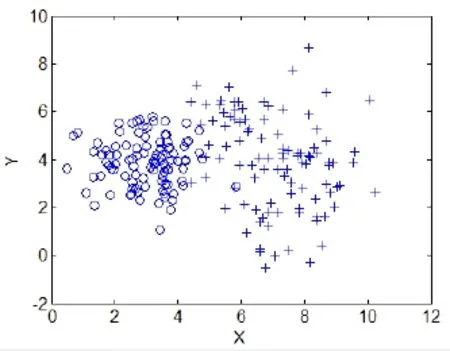
图2　随机生成的正态分布数据集2

3.2实验

在图1和图2所示的数据集中使用新提出的WFCMα算法和FCMα算法，取模糊度m=2，分类数c=2，截断阈值α=0.6，其他的初始条件也设置相同，执行上述两种算法，得到如表1所示的结果：

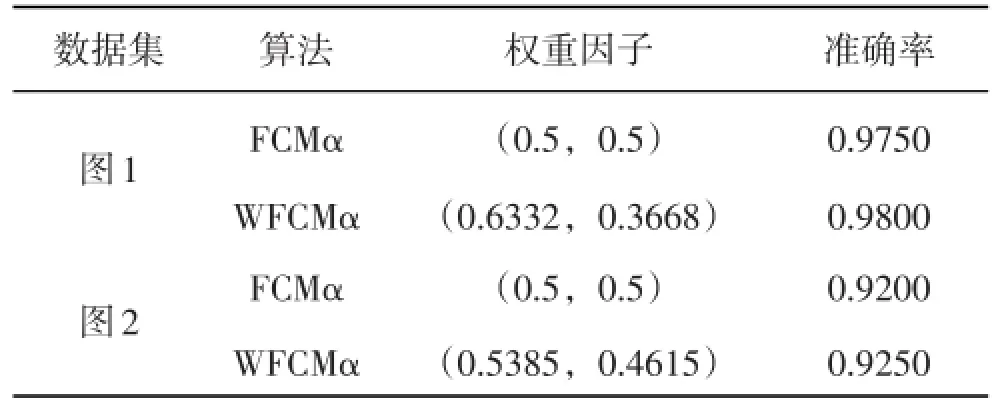
表1　WFCMα算法和FCMα算法对图1和图2数据集的聚类结果

从表1的结果可知，相对于FCMα算法的平均权重，WFCMα算法给出了更自然的权重因子，其聚类准确率也得到了一定的提升。以上是算法在人工数据集中的表现，下面进行真实高维数据集的实验。

实验二，在Iris数据集中分别使用WFCMα算法和FCMα算法，设定分类数c=2，截断阈值α=0.6，其他的初始条件也设置相同，在模糊指数m等于1.2，2.0，5.0，10.0的情况下，执行上述两种算法，得到如表2所示的结果：

表2　WFCMα算法和FCMα算法对Iris数据集的聚类结果

表2的数据表明，在真实的数据集中，WFCMα算法的表现非常优异，在不同的模糊指数下都取得了更好的准确率，聚类精度更高。这说明，相比较FCMα算法的平均特征权重取值，使用Bootstrap方法得到的特征权重更符合实际，基于Bootstrap的WFCMα算法也更有效。

4　结论

为了提高FCMα算法的聚类效果，在算法中引入Bootstrap统计方法，提出了基于Bootstrap的特征加权FCM改进（WFCMα）算法。仿真实验表明，相对于FCMα算法的平均权重，WFCMα算法得到的样本特征权重更自然，更适用于实际情况，改进后的算法也具有更好的聚类效果，更有效。

［1］袁正午，魏荣，叶明星.一种适用于基因表达数据的特征加权FCM算法［J］.计算机应用研究，2010，27（7）:2483-2485.

［2］蔡静颖，谢福鼎，张永.基于马氏距离特征加权的模糊聚类新算法［J］.计算机工程与应用，2012，48（5）:198-200.

［3］刘兵，夏士雄，周勇，韩旭东.基于样本加权的可能性模糊聚类算法［J］.电子学报，2012，40（2）:371-375.

［4］段林珊，刘培玉，谢方方.基于模拟退火的样本加权FCM算法［J］.计算机工程与设计，2013，34（6）:2004-2008.

［5］M.S.Yang，K.L.Wu，J.N.Hsieh，etal.Alpha-cut implemented fuzzy clusteringalgorithmsand switching regressions［J］.IEEE Transactionson Systems，Man，and Cybernetics，2008，38（3）:588-603.

［6］B.Efron.Bootstrap Methods--Another Look at the Jackknife［J］.The AnnalsofStatistics，1979，7（1）:1-26.

［7］C.L.Blake，C.J.Merz.UCI repository ofmachine learning databases.［http://archive.ics.uci.edu/m l/］.Irvine，CA:University of California，Departmentof Information and Computer Science，1998.

（责任编辑：潘修强）

Weighted Im proved Fuzzy C-MeansClustering Algorithm based on Bootstrap

HONGNian-song，FAN Yuan，GUOHua-feng
（Collegeof Information and Communications，Zhejiang Industry&Trade VocationalCollege，Wenzhou，325003，China）

To improve the convergence speed of the fuzzy C-means clustering algorithm，alpha-cut factor is introduced by Yang etal.and thealpha-cut threshold fuzzy C-means（FCMα）clustering algorithm is proposed，which accelerates the convergence.However，the FCMαalgorithm also has the problem of poor clustering effect.To solve the problem，the Bootstrap statisticalmethod isused to carry on the featureweighting，and theweighted im proved fuzzy C-mean clustering algorithm based on Bootstrap is proposed.The experimentsshow that the proposed algorithm hashigher clustering accuracy and beenmoreeffective.

FCM；alpha-cut threshold；Bootstrap；featureweighting

TP301.6

A

1672-0105（2015）03-0057-03

10.3969/j.issn.1672-0105.2015.03.013

2015-07-25

温州市公益性科技计划项目（G20140049），浙江工贸职业技术学院教师科技创新活动计划项目（X140203）

洪年松，硕士，浙江工贸职业技术学院讲师，主要研究方向：模式识别、图像处理；范渊，硕士，浙江工贸职业技术学院讲师，主要研究方向：图像处理；郭华峰，硕士，浙江工贸职业技术学院讲师，主要研究方向：图像处理、模式识别。