Gompertz模型在人口增长预测问题中的应用

阎慧臻

（大连工业大学信息科学与工程学院，辽宁大连　116034）

Gompertz模型在人口增长预测问题中的应用

阎慧臻

（大连工业大学信息科学与工程学院，辽宁大连116034）

Gompertz模型是常用的动物种群生长模型，可用于描述种群的生长发育规律。利用分离变量的方法求出了Gompertz模型的解析解，利用MATLAB软件描绘了Gompertz模型解析解的图形。基于Gompertz模型，运用最小二乘法，对1985—2012年中国人口数据进行非线性拟合，建立了中国人口增长的近似公式，运用此公式估算了中国历年人口数量，并对中国2020、2030和2050年的人口数量进行了预测。估算的中国人口数量与实际统计结果吻合情况良好。

Gompertz模型；人口数量；预测

0　引　言

中国是一个人口大国，人口问题始终是制约我国发展的关键性因素之一。人口预测就是根据现有的人口状况并考虑影响人口发展的各种因素，按照科学的方法，测算在未来某个时间的人口规模、水平和趋势［1］。众所周知，人口增长规律符合S型生长曲线。但在实际生活中，由于灾难、疾病等各种客观因素的干扰，使得人口增长的规律并不是理想中的完全对称的S型，因此，如果用Logistic模型［2］进行人口预测，并不能很好地描述人口增长的实际情况。Gompertz模型［3］是当前使用较多的用以描述生物种群生长发育规律的生长曲线模型。不仅如此，Gompertz模型在医学、软件开发、交通运输等领域的应用都非常广泛。作者利用Gompertz模型，以中国1985—2012年人口数据为依据，通过曲线拟合，建立了中国人口增长的近似公式，并对中国未来人口进行预测。

1　Gompertz模型

Gompertz种群增长模型的基本方程是

式中：y（t）表示在t时刻种群个体的数量；k称为种群的相对增长率，即平均出生率减去平均死亡率；M表示环境的最大容纳量。

式（1）的平衡点为y＝M。由微分方程稳定性理论［4］可知，y＝M是稳定平衡点。

1.1Gompertz模型的解析解

由于方程（1）是可分离变量的微分方程，因此分离变量即可求得式（1）的解析解：

令M、k及初值y0为下面两组数值：

①M＝60，y0＝15，k＝0.4

②M＝90，y0＝35，k＝0.8

将两组数值分别带入式（2），利用MATLAB编制计算程序，计算所得结果见表1。

1.2利用MATLAB软件描绘解析解图形

Gompertz模型解析解的图形可以利用MATLAB软件描绘。

令式（1）M＝90，k＝0.8，初值y0分别取为y01＝5，y02＝30，y03＝90，y04＝120，y05＝150。其中y01，y02小于M，y03等于M，y04，y05大于M。

利用MATLAB编制绘图程序，程序执行后得到Gompertz模型解析解的图形如图1。图1绘制了初值不同的5个解析解的图形。由图1可以看出，无论Gompertz模型的初值y0n是小于、等于还是大于环境容量M，随着时间t的无限增大，总有种群个体的数量y（t）→M，也就是说种群个体的数量将最终稳定在环境容量M上。

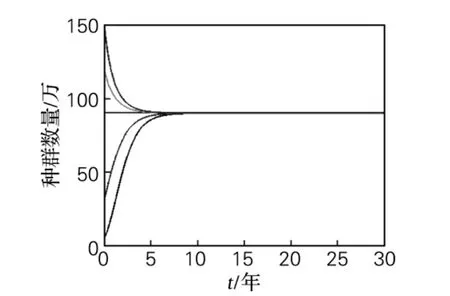
图1　解析解图形Fig.1　Figure　of　analytic　solution

1.3用龙格－库塔数值解法求Gompertz模型的数值解

龙格－库塔法是高精度的数值计算方法，在实际中有着广泛的应用。用MicrosoftVisual C＋＋编译软件编制Gompertz模型数值解的计算程序，计算结果见表1。

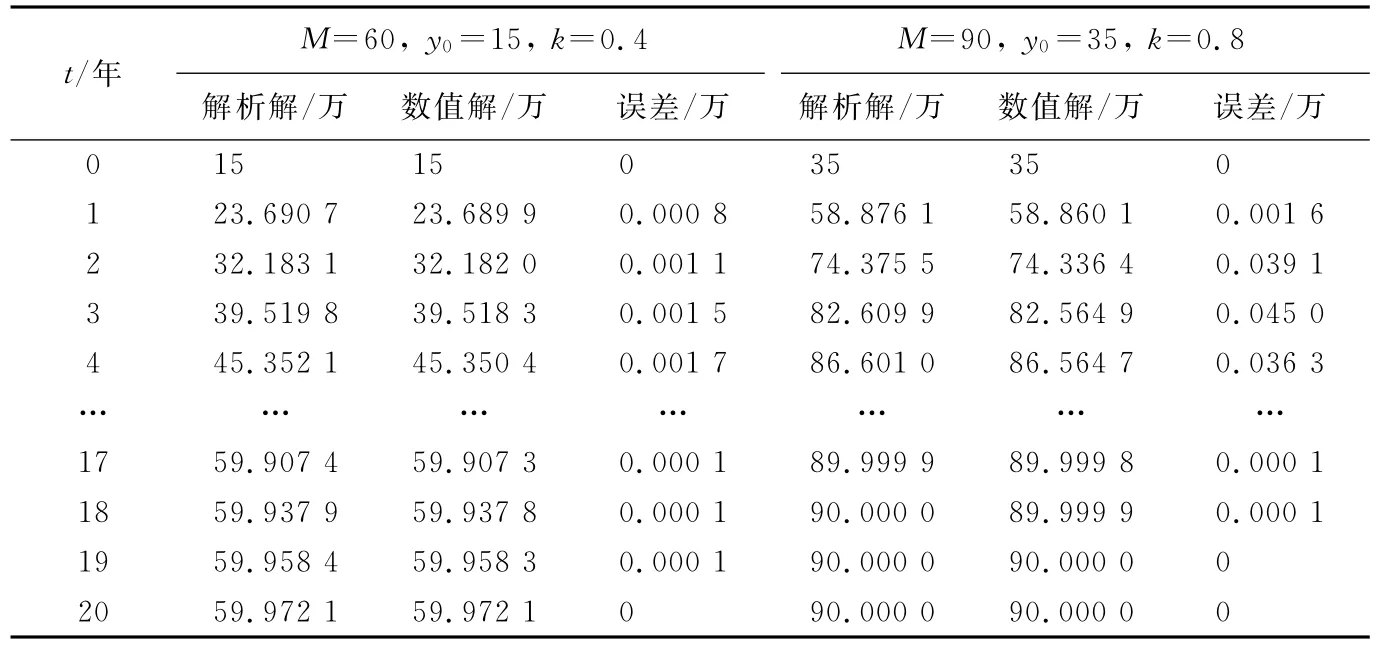
表1　Gompertz模型解析解与数值解Tab.1　Analytic　solution　and　numerical　solution　of　Gompertz　model

2　基于Gompertz模型的人口增长预测

在Gompertz模型中，当y（t）表示人口数量时，Gompertz模型即为人口增长模型。利用该模型对我国人口增长规律进行预测。模型（2）为三参数（M，β，k）S型增长模型，对于3个参数的拟合可以先确定其中的M，并通过变换将其线性化，这样便可由最小二乘法估计出另两个参数值。

式（2）取对数：

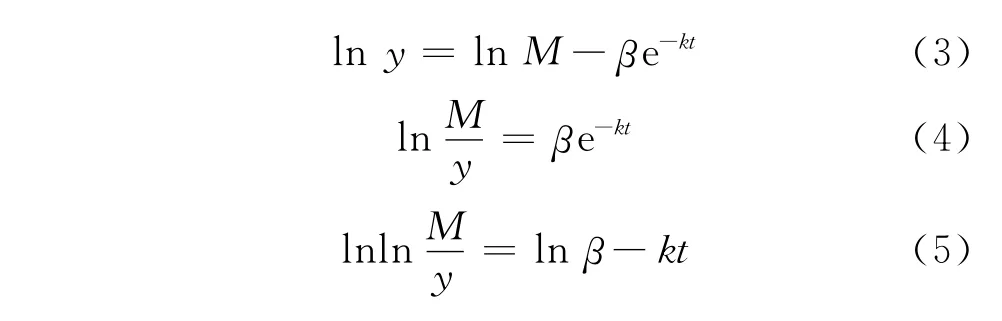
设n组观测值为（ti，yi），i＝1，2，…，n，取M＝ 20亿，令由最小二乘法得

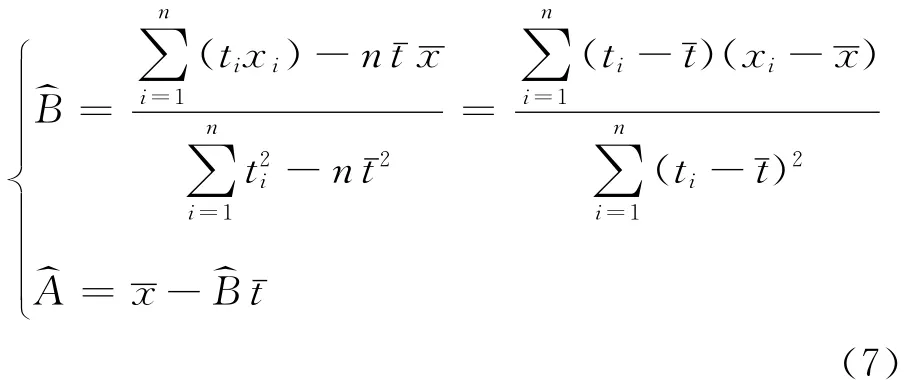
由文献［5］获得我国历年人口基本数据见表2。由于数据取1985—2012年，因此选择这28年相应的人口数据为观测数据：y0＝10.5851， y1＝10.7507，y2＝10.9300，…，y26＝13.4735，y27＝13.5404。

令1985年为0年，则t0＝0，t1＝1，…，t26＝26，t27＝27。

用MicrosoftVisualC＋＋编译软件编制数据拟合程序，利用以上观测值，得β＝0.6109532，k＝0.0178916，则

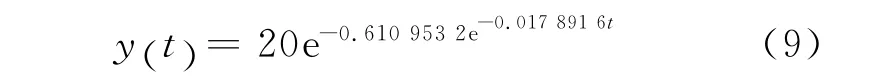
式（9）即为中国人口增长的近似预测公式，利用此公式，可估算中国1985—2012年的人口数量，结果见表2。从表2可以看出，利用Gompertz模型进行人口数量估算，估算结果与实际统计结果吻合良好。

表2　中国1985—2012年实际人口与预测人口Tab.2　Actual　value　and　predicted　value　of　China　population　from　1985to　2012

利用人口预测公式（9）分别对我国2020、2030、2050年人口数量进行预测，结果见表3。

表3　中国人口数量预测值Tab.3　Predicted　value　of　China　population

3　结　论

利用Gompertz模型及已知的28年人口统计数据，给出了中国人口增长规律的预测公式。利用此公式，估算了中国1985—2012年的人口数量。结果显示，用此预测公式对我国人口进行估算的结果与实际人口数量吻合很好，最大预测误差为2.5655%。同时，运用此公式，给出了中国2020、2030及2050年人口数量的预测结果，预测值分别为：2020年约为14.4271亿，2030年约为15.2201亿，2050年约为16.5233亿。

［1］蒋辉.我国人口预测分析［J］.科技管理研究，2005（11）：142－145.

［2］阎慧臻.Logistic模型在人口预测中的应用［J］.大连工业大学学报，2008，27（4）：333－335.（YANHui－zhen.ApplicationofLogisticmodelin populationprediction［J］.JournalofDalianPolytechnicUniversity，2008，27（4）：333－335.）

［3］辛秋红，尹海东.基于Gompertz模型的黑龙江省人口预测［J］.统计观察，2008（23）：82－83.

［4］马知恩，周义仓.常微分方程定性与稳定性方法［M］.北京：科学出版社，2004：41－51.

［5］中华人民共和国国家统计局.2012中国统计摘要［M］.北京：中国统计出版社，2012：39－40.

ApplicationofGompertzmodelinpopulationprediction

YANHuizhen
（SchoolofInformationalScienceandEngineering，DalianPolytechnicUniversity，Dalian116034，China）

Gompertzmodelisacommonlyusedmodelforbiologicalpopulationgrowth，whichcan describethelawsofpopulationgrowth.Inthispaper，theanalyticalsolutionofGompertzmodelis obtainedwiththemethodofseparatingvariables，andthefigureofanalyticalsolutionisacquiredwith thehelpofMATLAB.Thenanapproximateformulaisestablishedbydoinganon－linearfittingtothe actualpopulationsofChinafrom1985to2012withGompertzmodelandtheleastsquaremethod，and thepopulationsofChinaarepredictedbyusingthisapproximateformula.Theresultsshowedthatthe calculationswereinconformitywiththestatisticaldatainprinciple.Atlast，thepopulationsofChina in2020，2030and2050canbepredictedbyusingtheapproximateformula.

Gompertzmodel；population；prediction

O29；Q141

A

1674－1404（2015）02－0150－03

2014－08－07.

辽宁省教育厅科技研究项目（2009A075）.

阎慧臻（1965－），女，教授.