场内敛平衡方程组
2015-10-08王明理
王明理

【摘 要】万有引力与电荷力的形成机制是自然界最复杂、最深刻的自然规律,本篇论文用“等价场力学”思想实现磁力、弱力、强力和引力的统一。场内敛率◎包含5个方面的内容:(1)对象体系整体性的◎值、所表示的为该体系的运动能力;(2)对象体系在空间的◎值分布规律;(3)一个体系在空间各区域场内敛以及场失衡的程度;(4)若干个独立体系相互场扰动在“群”的中心所能达到的最高◎值;(5)单元体系在群内的系统性表现。一个体系的“非平衡区”随其体系◎值的增加而内移、伴随“非平衡区”内移其“场平衡行为”因信息传递的距离变小其磁场的波动周期变小,物质◎值在0.5≤◎≤1区间内其外部近程上的力学作用不在表现有电荷性但其远程上系统性的电荷性存在并未消失。物质远程力与近程力的主导性博弈是本篇论文价值的精髓之一,对象体◎值不同其远程力(负电性的成份)的主导程度不同从而使对象体的磁场在空间以光速C所运行的轨迹不同,◎值高的对象体其磁场信息更倾向于向远方直线运行、◎值低的对象体其磁场信息更倾向于在近距空间涡旋。“◎h值守衡张量”是自然界体系性对特定空间出现的增加其“场平衡态下◎h值”的阻遏力,“场张量”的大小随“场平衡态下◎h值”的增大而增大、力的方向为逆心力方向,“场张量”是一个矢量其造成“宇称守恒”的时间不对称。
【关键词】场失衡能QE;惯性质量的正负性;反电荷间远程引力;辐射力力程方程;远程力与近程力主导性博弈方程;饱和型场平衡;范场与阱场;◎h值守衡张量
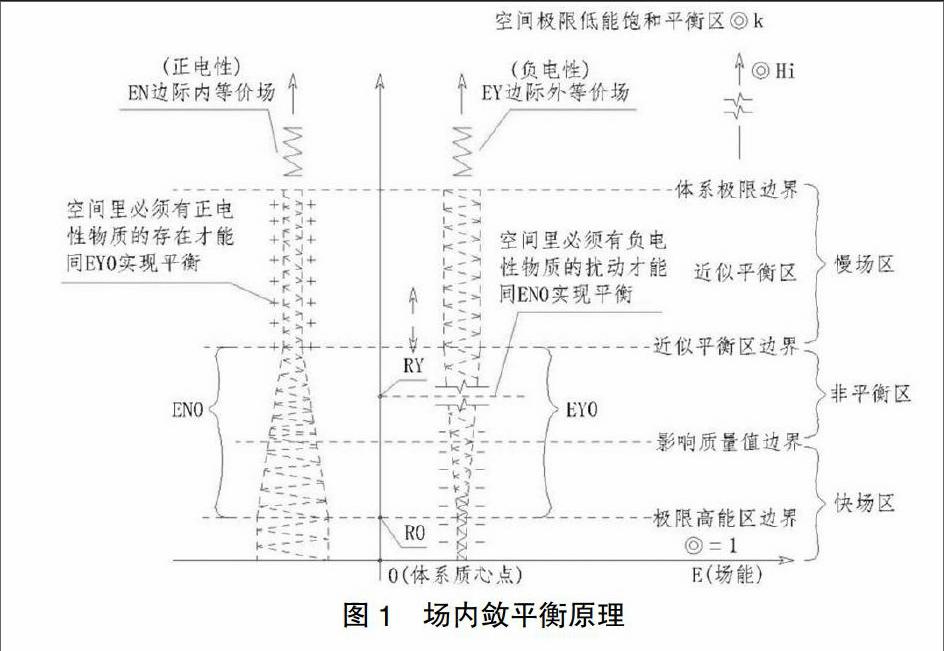
1 场内敛平衡原理(图1)
任何物质都在自体的外部存在一个与自体质能值相等的等价场体系,等价场体系由边际内等价场体系(EN)与边际外等价场体系(EY)构成且场能值EN=EY,EN与EY的磁场流分布规律为反对称的关系、EN与EY交替向外部空间衍生,以整体来看EY体系位于EN体系的外部、空间的位置关系使EN磁场能量的密度以极微小的程度大于EY,等价场体系在其存在范围内系统性的受到空间里“磁波”的扰动进而发生场内敛,EN与EY场能量密度的差异性导致两者场内敛的程度不同、EN内敛的程度大而EY内敛的程度轻,等价场这种内敛效应的偏置性最终积累于一个体系的近距空间,场内敛的能量造成其所存在空间的场失衡,场失衡需要特定物质对所在空间的边际外等价场进行扰动使其场内敛的程度与边际内等价场达到平衡。宏观星系等价场的失衡性需要若干特定的物质体对其扰动以使整个体系实现场平衡,从宏观星系的角度看物质存在是一个体系实现场内敛平衡的手段,物质在实施“场内敛平衡”的行为中被赋予动能,物质的运动属性是所在体系实现场内敛平衡的需要。
2 慢场区、非平衡区、快场区(图1)
体系场内敛的能量所沉积的区域将其称为“非平衡区”,“非平衡区”随体系的速度增加而内移或随体系场内敛率的增加而内移、从而使体系场平衡信息传导的距离发生改变、进而使体系场内敛率的波动周期发生改变。在一个宏观体系的空间里◎>0.5区为EN0>EY0、◎=0.5区为EN0=EY0、◎<0.5区为EN0 3 万有引力的形成机制(图1) 自然界任何物质都具有一定值的引力,与磁力相比物质所具有的引力极为微小。在“等价场力学”中电荷力、弱核力、强核力的终极来源都由体系的万有引力所赋予,“等价场力学”用“静态场内敛率对应性关联方程”来表述一个体系万有引力的作用。物质等价场体系在空间里相互扰动,扰动的结果使物质的等价场体系发生场内敛和场失衡,“等价场力学”用“场内敛率◎”来表示一个物质单元场内敛的程度或一个体系内某一位置上空间场内敛的程度,场内敛的能量引发其所沉积空间的场失衡,空间的场失衡需要特定物质对所在空间的等价场体系进行扰动来实现场平衡,物质体系场内敛的程度决定其远程上与近程上场扰动的能力。 “等价场力学”用对象体的“场内敛率”来描述物质体系相互间引力与斥力的关系,一个体系有若干个物质单元构成,物质单元相互间会产生对各自等价场的扰动,扰动的结果在体系的中心区域场内敛率最高,各物质单元按自体在体系内所存在的位置来获得特定的“场内敛率”,场扰动不仅使自体的场内敛率增加也引发体系内其它对象体场内敛率的增加,在一个宏观体系里其宏观单元体只能存在于同自体的◎i值完全相同的空间里。 对象物质在不同的◎h值环境里其◎i值会发生变化这是“等价场力学”一个极重要的规则,在◎h=1的环境里物质的场内敛率最高、同环境◎h=1不对应的低◎值物质不能够到达该区,在◎h=1环境里同为负电荷性的对象物质其相互间在近程上场扰动效用发生的作用力极其微小、单元体相互间的向心力近似于零值呈现为自由态、向心环绕速度近似于零值各自近似于静止态,◎i≥0.5的物质在离开高能空间到达低能空间后其场内敛率会一定程度的变小,场内敛率◎值反央的是一个物质体系其磁场内敛的程度和一个物质体系其磁场在空间各区域场失衡的程度。场内敛率◎以物质体的运动速度为基准而建立,物质体的速度在其◎i≥0.5而其◎h≤0.5条件下为光速并达到最大值,考虑到◎h环境的影响物质体在◎h>0.5的环境里速度会变慢、◎h=1时物质体的速度等于◎i≌0所对应的速度,物质体◎i值的降低需要一个极其漫长的时间来进行释放。“物质群”的质量值越大以及“群”内单元物质的◎i值越高、在其“物质群”外部空间所存在的“场平衡施体”就会越多,这些“场平衡施体”是“物质群”以一个体系存在的屏障与力学基础,“物质群”的规模太小其“场平衡施体”的规模就会太小、体系整体上的磁场规模就不能够阻断其中心区高◎值质心体与外部空间的反电荷远程引力作用。
物质体◎值若发生变化其运动能力、电荷量以及电荷性质都会发生变化,低速物质◎值变化对其场形态的影响不大,高速的光子类物质◎值变化对其场形态的影响就会非常大,频率的差异与场形态特征的差异影响对象粒子间的场扰动能力,◎值相同的粒子其频率相同、场的形态特征也会极相似、相互间能够达到最佳的扰动效果。
一个体系质量值的规模与体系R0区体积的大小成正比,有若干个单元体构成的体系、体系中心区所能达到的最高场内敛率取决于体系质量的总规模。物质体系的合并由各自“慢场区”的部分共有开始,“慢场区”的中心点为体系的场心点,体系内单元体场内敛率的分配以体系的场心点为基准点按“静态场内敛率对应性关联方程”来分配,主体质量值相对于客体越大或客体的分布越均匀其体系场心点与体系主体的质心点两者吻合的程度越高,主体质心点与体系场心点间的距离大小决定其客体轨道的偏心率,客体轨道进动的产生与主体围绕场心点的运动周期有关而该周期取决于主体在体系内的◎值分配。
“等价场力学”将引力分为3个类别:(1)单元体相互间的扰动能力所产生的引力;(2)场平衡施体与场失衡主体间的引力关系;(3)性质为反电荷间相互远距作用的远程引力,“慢场区”物质为正电荷性、“快场区”物质为负电荷性,“慢场区引力”具有均匀性和分散性2个特征,光子的◎i≥0.5在其离开高能空间的屏蔽后受到“反电荷远程引力”的作用,当光子成为近似◎k值的正电性物质时其只能存在于一个星系外围的“慢场区”。
4 惯性质量的正负性
(8)物质的动能质量VM公式
VM=M×◎;
M为一个物质体系的质量值,◎为该体系的动态场内敛率;
(9)物质的阻动质量FM公式
FM=M×(1-◎);
M为一个物质体系的质量值,◎为该体系的动态场内敛率;
(10)惯性质量GM公式:
GM=(FM-VM)=> GM=M×(1-2◎i);
当物质◎i<0.5时成为正质量物质;当物质◎i=0.5时成为电中性物质;当物质◎i>0.5时成为负质量物质;
当物质◎i≥0.5、◎h≤0.5时其惯性质量为零值。
5 场内敛平衡方程组
(1)场内敛率公式组
◎k≤◎≤1 ; (◎k为自然界所存在的极限最低场内敛率)
Vi=◎i×2C;Vi≤C;(◎i=◎h;◎h≤0.5;◎i为对象体系的场内敛率值,◎h为对象体系所在环境的场内敛率值;C为光速,Vi为对象体的向心环绕速度其大小由所在环境的场失衡程度所赋予;)
Vi=C(1≥◎i≥0.5;◎i≥◎h;◎h≤0.5;C为光速;)
Vi=(1-◎i)×2C;Vi≤C;(1≥◎i≥0.5;◎i=◎h;◎h≥0.5;C为光速;)
(2)静态场内敛率对应性关联方程(场平衡效率方程)
◎i=RO/√Ri;(天体或物质体的质量值与其常数半径RO值的体积成正比,在一个体系内只要测得其任意一个环绕客体“场平衡态下的公转周期与轨道半径”(无需知道该环绕客体的质量值)就可以计算出所在体系的常数半径RO值,不同于牛顿力学这是一种完全崭新的质量计算方法,太阳系八大行星可分别独立计算出大致相同的(太阳系的)常数半径RO值,太阳系中太阳与其各行星的RO值见表1)
(◎i为对象体的场内敛率值或一个体系场内敛率值在周边空间距离上的分布,RO^2为一个体系场内敛率◎=1的区域,Ri为对象体到体系中心的瞬时距离,施体的Ri越小其场平衡的效率越高说明所在空间场失衡的程度越大。)
(3)场失衡能QE(图1)
QE=EN0-EY0;
(QE为物质体系携带的能量,EN0、EY0分别为边际内等价场体系与边际外等价场体系在“非平衡区”两者对应场的总能量值,在空间里只要有磁波这种传播方式的存在EY0就不可能与EN0绝对等值,◎k为自然界所存在的极限最低场内敛率、场内敛率为◎k的物质其位移速度近似于静止。)
物质体速度增加其“非平衡区”内移,在◎≤0.5区间物质体场失衡能QE随其速度增加而减小,正电性粒子的特征体现在其“非平衡区”距离其中心较远,物质的◎=◎k时其QE为正最大值、并在远程上具有最大的力学效用,宏观天体最外围粒子的场内敛率值最低。1≥◎i≥0.5区间粒子的近程作用效果呈电中性但其负电荷性并未消失,体系近距上的负电荷性(QE为负值)以体系远距上大范围系统性存在的正电性(QE为正值)存在来实现(图1示),体系近距上的正电荷性(QE为正值)以体系远距上大范围系统性存在的负电性(QE为负值)存在来实现。
(4)辐射力力程方程
Rf1=(R0/◎i) ^2×@1;
(Rf1为光子的辐射力力程,R0为该体系的常数半径,◎i为辐射粒子所在空间的场内敛率值,@1为一个常数)
(5)电荷力力程方程(远程力与近程力主导性博弈方程)
Rf2=(1-2◎i)limQE×@2 ; (Rf2为粒子远程上的电荷力力程,◎i为该粒子的场内敛率值,limQE为该粒子所携带的最大值电荷能,@2为一个常数;)
◎i=0.5时粒子的电荷力力程为零值;◎i≌0时粒子的正电荷力力程达最大值;◎i=1时粒子的负电荷力力程达最大值,“非平衡区”过度内移使物质在近距上力学作用的能量被压缩导致场内敛的能量在空间无法产生场扰动效用,“非平衡区”过度内移使体系力学作用所依赖的“场非平衡区”变成高度场平衡的近似中性区,高◎值使体系整体性、系统性变为均匀极弱性的EN0
(6)粒子场内敛率与电荷量的关系
QEi=(1-2◎i)limQE;=>◎i=0.5-QEi/2limQE;
(QEi为物质动态所携带的电荷能,◎i为物质动态的场内敛率,limQE为物质最大值的场失衡能;◎i<0.5时物质带正电荷,◎i>0.5时物质带负电荷,◎i=0.5时物质呈现为电中性;)
(7)光子对体系的场内敛率贡献率
QEg=(1-2◎g)limQEg;
(QEg为光子动态所携带的电荷能,◎g为光子动态的场内敛率,limQEg为光子最大值的场失衡能,◎g≌0时光子带有最大值的正电荷能,◎g=1时光子带有最大值的负电荷能,带正电荷物质的“非平衡区”距离其中心较远具备可测量条件,带负电荷物质的“非平衡区”距离其中心较近可测量条件差,高◎的负物质其场体系表现为系统性以极高程度均匀性的弱电性存在、而在近区则表现为极高程度的场平衡性。
(0.5-(QEg+QE)/2limQE)=◎
(QEg为光子动态所携带的电荷能,QE为体系所携带的电荷能,limQE为体系最大值的场失衡能;◎为光子被体系吸收后体系所达到的场内敛率值)
光子与光子间因电性相同不存在电荷性引力只存在万有引力,“光子群”的规模如果非常小在其外部自然界中就不会存在能满足其场平衡条件的合适“场平衡施体”,由光子为单元构成的扰动体系符合“静态场内敛率对应性关联方程”的场内敛率分配规律,非近距接触的光子其“范场”与“阱场”不能够为相同态,场扰动不仅使自体的场内敛率增加也引发体系内其它对象体场内敛率的增加,一个群内的光子单元体其场体系拥有共同的部分,一个光子的场内敛率增加等价于该粒子对体系内其它单元体的扰动能力增加、并致使体系内其它单元体的场内敛率同步增加,对象光子间距离大到一定定值时其场体系实现较大程度的分离致使其“共同场部分”相对丧失、进而使光子单元体间量子纠缠的同步性丧失。
6 中子电中性的形成机制
中子的场内敛平衡由数量众多的光子完成,光子群对中子边际外等价场的扰动行为是以全方位角覆盖的方式来进行的,这种特性使质子的EY0相对以更大的效率实现了其体系场内敛的平衡,上述特征在源头上由中子所在空间特定场内敛率值的环境所赋予,也就是说在源头上并不是光子群赋予了中子较大的◎值。在原子体系里质子的场内敛率要低于中子,用“等价场力学”原理可以推理出中子位于原子体系相对接近中心的位置而质子位于次中心的位置,中子的较大场内敛率值由原子体系内其它单元体的场扰动所赋予,物质群内属性相等的粒子随时间推移其单元体◎值的等值性会被打破从而形成层次性分布。中子在离开原子体系后其所在新环境的场内敛率变小就要回归到新环境影响下的场内敛率,中子非平衡区的能量包含2部分:(1)体系场内敛的磁场能量、(2)对“非平衡区”进行场平衡的物质粒子;这两部分的能量值相等两者的关系为反对称的关系,在中子“非平衡区”外移过程中这两部分的反能量合并,合并的结果就是将特定空间的场内敛率增加形成新物质,“反中微子”为“非平衡区”场内敛弱势的EYO部分,电子为“非平衡区”场内敛强势的ENO部分与“EYO部分存在的场平衡施体”两者的合并体。
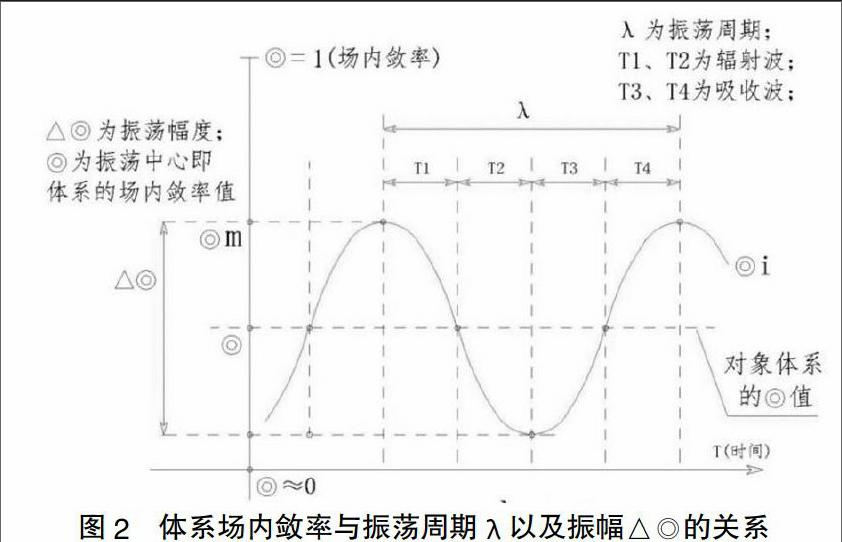
7 体系的场内敛率振荡周期与体系场内敛率值的关系(图2)
物质体的场内敛率越小其◎值振荡周期越长、振幅越大,物质◎值的振荡周期与其◎值成反比。在物质的◎≌0时其电磁波的振幅中心将在◎=0的附近。
(12)振荡周期λ与物质◎值的关系
λa/λb=△◎a/△◎b=◎b/◎a;
λa、λb为物质体场内敛率的振荡周期,△◎a、△◎b为物质体场内敛率的振荡幅度,◎a、◎b为物质体的场内敛率振幅中心(图2所示)。一个体系的◎值越大其“非平衡区”距离体系中心的距离越小,光子的◎值越大其“场平衡行为”所发生的空间距离光子越近、体系对场平衡调整信息的传导就越快、从而使光子的波动周期与波动幅度变小;现实中光子因速度极高其速度以匀衡的方式存在。
8 电子场内敛率与质子场内敛率的关系(图3)
质子◎<0.5,质子如果增加其◎值将减小其QE向电中性粒子发展,质子吸收一个光子后引起边际外等价场EY0场内敛的程度增加,电子存在的作用就是对质子的EY0进行扰动使其场内敛的程度与EN0场内敛的程度实现平衡,质子吸收一个光子后场内敛率的增加使其QE减小、QE减小直接使电子的动能减小,电子一定程度的外移使质子在吸收一个光子后达到新的平衡,电子外移的惯性使质子边际外等价场EY0场内敛的程度减弱从而导致质子的QE增大,质子QE的增大使质子赋予给电子的动能增加、进而引发电子内移,电子内移引起质子场内敛率的增加,电子到达内移的极限位置时质子要释放光子,电子到达外移的极限位置时质子要吸收光子;电子外移时只有释放出光子才能降低其自体的场内敛率、才能到达低能区,电子内移时只有吸收光子才能增加其自体的场内敛率、才能到达高能区。
(13)◎p=◎e;(◎p、◎e分别为质子与电子场内敛率的振幅中心)
(14)△◎e×sin(ψ+∏)/2+◎e=◎pi;(△◎e为电子的场内敛率振幅,ψ为电子的瞬时相位角,◎e为电子的振荡中心,◎pi为质子与电子在同一个时间上所对应的瞬时场内敛率值。)
(15)◎g=◎m; (◎g为质子所辐射光子的场内敛率,◎m为质子场内敛率振幅的极限上值)
9 饱和型场平衡
“微观粒子其等价场体系在空间有非常大的存在范围,近距上的场内敛程度由粒子等价场体系系统性的特性所造成,“饱和型场平衡体系”是一个体系近距上的场失衡状态与其等价场体系全范围完全实现深度平衡的体系,“饱和型场平衡”是一个物质体系在极大的空间里经过极长时间的传导过程才能系统性完整的实现与环境真正对等的高能或低能的场平衡。
低能空间的本质是存在较小的场失衡能(QE)其能够实现较高程度的场平衡,高能空间的本质是存在非常大的场失衡能(QE)而其能够实现极高程度的场平衡,从体系的整体性来讲◎值近似于0.5的物质具有最高程度的场平衡,低能物质在近距上的局部以快速的方式实现场平衡达到高能状态、这种平衡的本质为局部平衡,因为其等价场体系里系统性场失衡能(QE)的存在会迅速将体系近距上场内敛所集聚的能量稀释掉。人工高能所造新物质的寿命取决于其单元体系所具有“饱和型场平衡”的成分。
10 范场与阱场(图4)
在“体系场内敛的平衡”这篇论文中对“空间旋极限性全无阻合并”进行了描述,如果没有宇宙背景的“宇宙平衡系统”场内敛率◎就会具有无限性,最终物质就无法以单元体的方式进行循环,同时空间将是“一体、连续的静态空间”,宇宙空间场内敛的极限性只能同宇宙背景的“宇宙平衡系统”达到平衡态,即使在宇宙场内敛极限区的内部其空间的独立性与系统关联性这两个特征不会发生任何改变、这样物质体系的能量循环才能具有系统性关联的可能,有了宇宙背景的“宇宙平衡系统”自然界只要“空间旋合并”这种形式存在、“空间旋体系”就必然会受到空间里磁波能量的扰动进而产生场内敛现象,“空间旋体系”发展到一定规模其中心空间的场内敛率在达到◎=1后这一区域就必然要诞生出物质,星系的场体系中只有存在了场失衡状态天体才能够实现在空间的独立存在,而星系的演化取决于宇宙空间慢物质的分布趋势,慢场过于强大的星系其慢场部分会形成新的星系,“饱和体系”不能够支撑宇宙里所有星系都处在成长趋势,“饱和体系”的规则是体系内只能永恒性一半处于成长趋势而另一半处于衰弱趋势。
“范场”的定义:“空间旋合并体”的中心以光速C在空间位移的轨迹,“阱场”的定义:“空间旋体”以光速C在空间位移的轨迹,物质的定义:在一个局部空间里有若干个“空间旋合并体”的集合,集合的规模因场内敛使中心区出现了高密度的能量特征,集合内是其单元体间“同向范场”与“同向范场”的合并以及“同向阱场”与“同向阱场”的合并,一个体系内的单元构成具有同一的范场方向和阱场方向,一个体系内在同一条轨道上的物质体如果范场的方向相同、范场的倾角相似两者最终会合并成一个体系。在客体与主体◎值近似的条件下、在一定值的距离内两者范场的方向与范场倾角会自动调整为同一态进而合并为一体,◎值不相似的两个对象体不能够近距离的合并为一个体系。
11 ◎h值守衡张量对宇称守恒的影响(图5、图6)
◎值变化
空间环境的场内敛率◎h值为一个体系系统性场平衡的结果,“◎h值守衡张量”是自然界体系性对特定空间出现的增加其“场平衡态下◎h值”的阻遏力,“◎h值守衡张量”简称为场张量,场张量的大小随环境“场平衡态下◎h值”的增加而增加,场张量为一个矢量具有方向性,场张量的方向为逆心方向。如果对象物质增加了所在空间“场平衡态下的◎h值”或者改变了“场平衡态下◎h的运行规律”就会受到体系场张量的作用力。
弱相互作用为对象体◎h值由高能态向低能态发展、对象体“非平衡区”的运行规律表现为外移与场张量的方向相同。正物质转变为其对称的反物质其实质是由低能态转变为高能态、其“非平衡区”的运行规律表现为内移与场张量的方向相反,正物质在其◎值增加的过程中受到体系场张量的阻遏力,负物质转变为其对称的正物质其实质是由高能态转变为低能态、其“非平衡区”表现为外移与场张量的方向相同。
事物由内向外发展为内因性、事务由外向内发展为外因性,外因性的特征为相对的由面及点,外因性使对象由低能态发展为高能态对“场平衡态下环境”的影响更大,内因性的特征为相对的由点及面,内因性使对象由高能态发展为低能态对“场平衡态下环境”的影响相对小,外因性所受体系的场张量大于内因性所受体系的场张量,场张量的规律说明物质任何方式的演化其本质都是对特定空间场平衡态的打破。
正物质与反物质湮灭的本质是一对低能反物质其等价场体系的合并,在空间完全性重组过程中产生巨大的能量使一对对称粒子的场内敛率都发生了增加,当两个粒子的核心区都达到最高场内敛率时具备了逃出合并体系的条件,大质量粒子在其外围必然存在场平衡施体而这些场平衡施体会将大质量粒子质心高能部分反电荷性质的远程力屏蔽起来,也就是说自然界只有质量值极小的“能量空间”能够获得自由,光子的“场平衡施体”不是物质而是场。在高◎值区如果自然界存在规范性限制那么这些逃出来的自由体的大小也必然存在限制因为如果其总能量值太大的话这些自由体根本逃不出所在体系,大质量值的高◎“物质体系”离开特定的高能环境后在其场平衡施体的作用下会迅速转换为质量值更大的低能物质。光子质量值的规范性来源于自然界◎=1的规范性,而◎=1必须建立在空间是系统性、规范性存在的基础上(图6)。
“场平衡态下◎h值”的增长性波幅越大场合并过程中受到体系的阻遏力越多、受阻遏力越多的场合并重组过程其周期相对要长(图6),“◎h值守衡张量”与“场平衡态下◎h值”所能增加的程度存在对应性关联,“◎h值守衡张量”造成物质宇称守恒中的时间不守恒。
对象体◎值不同其远程力(负电性的成份)的主导程度不同从而使对象体的磁场在空间以光速C所运行的轨迹不同,◎值高的对象体其磁场信息更倾向于向远方直线运行、◎值低的对象体其磁场信息更倾向于在近距空间涡旋,物质远程力与近程力的主导性博弈使对象体◎值不同其运动轨迹也相应不同,远程力占主导性的物质与近程力占主导性的物质在总体上比较两者的手征性相反,远程力占主导性的物质为负电性其运动性质为反电荷间的远程引力作用(逆心的张量力),近程力占主导性的物质为正电性其运动性质为体系场平衡施体的向心力运动,反电荷间的远程作用力完全具备张量力的特点,张量力:(1)力源的方向可任意性、(2)只要◎i>◎h任何空间对于“物质体”均都表现为斥力、(3)存在范围◎h<0.5、(4)张量力为斥力。光子的运动是张量力与反电荷间远程引力两者作用的叠加,当◎i=◎h时张量力就不存在了对象与空间仅表现为场平衡施体的关系,◎i=◎h为场平衡态。
弱相互作用的本质是对象体系的◎i值大于其存在环境的◎h值,在场张量的作用下体系的◎i值逐步向◎h值回归,伴随着对象体系“非平衡区”的外移其辐射粒子的频率对应性同步降低。弱相互作用中粒子发生衰变的环境决定其“非平衡区”外移的程度,一个体系存在环境的◎h值变化越大其需要吸收或释放的能量也越大、进而影响体系内新物质系形成的规模。
[责任编辑:汤静]
