基于有限元方法的高温高压空气导管的应力分析

刘超

【摘 要】在详细分析空气导管所受到的载荷、飞机结构的约束及其对管系作用机制的基础上，以某型飞机空气导管为例，采用有限元分析方法，对管系进行应力分析，并据此基于米塞斯校核标准对管系进行应力安全性评估。同时，考察了球形接头的特性参数对管系应力集中程度的影响。研究结果表明：球形接头的补偿效果随着最大转动角度的增大而增大，随着起动力矩的增大而减小。

【关键词】空气导管系统；有限元；冯米塞斯准则；应力补偿

【Abstract】Based on the analysis of the loads of pneumatic duct system， constraints of aircraft structure and its mechanisms applying to the duct system， the finite element model of the pneumatic duct system in a certain aircraft was developed and static analysis was carried out by means of finite element method. Using the Von Mises criterion， stress safety evaluation was established according to the stress results. Meanwhile， effects of ball joint property on the stress performances of the duct system were also investigated. The results of the study show that stress compensation effect will be improved by the bigger maximum bending angle and the smaller starting moment.

【Key words】Pneumatic duct system； Finite element； Von Mises Criterion； Stress compensation

0 引言

空气管理系统是飞机的重要机载系统之一，其作用是负责完成飞机座舱压力、温度、湿度、供气量、空气品质等参数的调节和控制，电子设备的冷却，发动机和机翼防冰，燃油箱、液压油箱和饮用水增压以及为发动机启动提供气源等[1-2]。空气导管作为高温高压空气的载体，是飞机空气管理系统的重要组成部分。导管不仅需承受高温高压空气施加机械应力和热应力；同时导管与机身之间的连接部件还会将飞机机动载荷引起的结构位移和振动传递给管道，影响约束边界，形成附加应力；由于导管穿过机翼、发动机吊挂、机身等多个区域，应力集中引起的管道形变和疲劳破裂，不仅影响空气管理系统功能的实现，而且会给其它系统的安全带来隐患，因此在设计阶段对空气导管系统进行详细的应力分析与校核是非常重要的。本文在分析空气导管受到载荷、约束等边界条件的基础上，采用有限元分析方法，基于米塞斯强度准则，对空气导管系统进行应力分析与校核，并考察各种不同边界条件对管系应力分布的影响。

1 计算对象及校核准则

1.1 计算对象简介

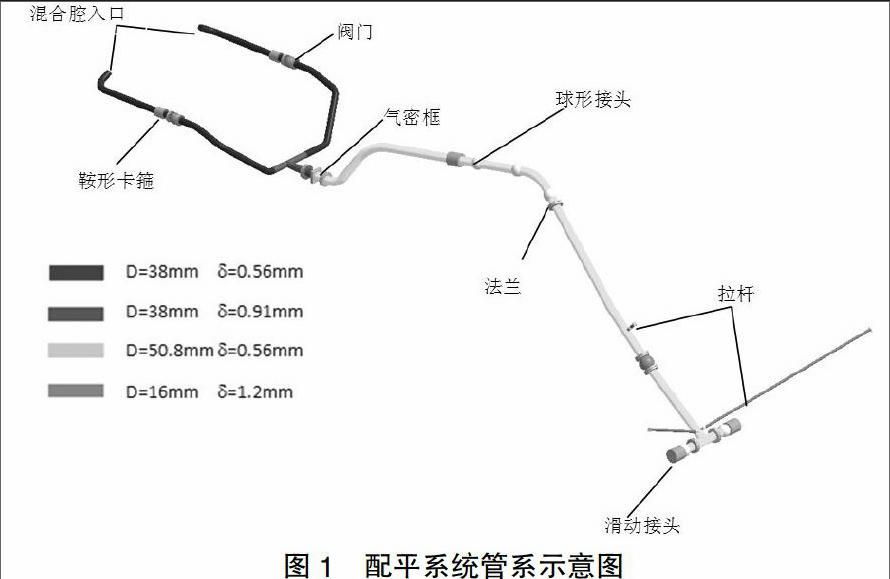
以某型飞机配平导管系统为例，导管与飞机气密框处固定连接，将配平系统分为两个部分，两部分之间不传递力和力矩，气密框下游的部分称为Part1，隔舱壁上游的部分称为Part2，如图1所示。

由图1可知，配平系统的管路主要由导管、导管连接件、补偿装置、阀门、支撑结构等组成，管系结构复杂。支撑结构和补偿装置的布置直接影响了管路系统的应力和位移特性。

1.2 校核准则

在应力计算中，由于不同材料、部件的物性和结构特性存在差异，相应的应力判据也有所不同，同时不同载荷产生的应力集中对材料的破坏程度不同，选择合适的应力准则是应力计算的基础，目前主要的应力准则有：最大拉应力理论，最大伸长线应变理论，最大切应力理论和米塞斯屈服准则等。其中，米塞斯屈服准则是指在一定的变形条件下，当材料的单位体积形状改变的弹性位能达到某一常数时，材料就屈服。它更符合金属管道的特性分析[3]。本文即以米塞斯屈服准则作为判据，进行管道应力计算和安全性判断。

2 管系有限元建模

2.1 系统建模

由于空气导管为薄壁结构，因此采用壳单元来模拟导管结构。而对于导管系统中的阀门、法兰、拉杆、鞍形卡箍、球形接头及滑动接头等部件的建模，是通过对这些部件的功能模拟来反映其对管系的作用效果。

2.1.1 拉杆

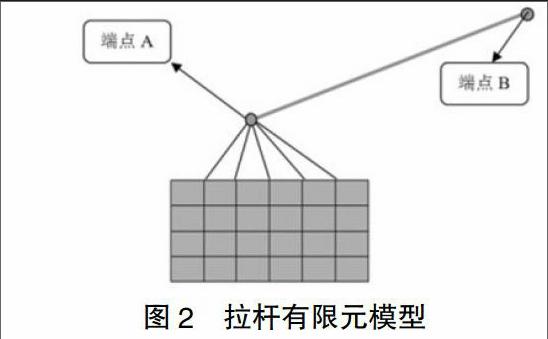
拉杆对空气导管系统起到支撑重量、约束位移变形和防振的作用[4]，并能补偿一定的安装公差，其示意图如图2所示：

由图2可知，拉杆通过“rod”单元进行模型，分别释放端点A和端点B的三个转动自由度，约束其三个平动自由度。

2.1.2 滑动接头

滑动接头（Sliding seal）可进行轴向补偿，并能在任意方向内转动。但其在各个方向运动的幅值有一定的要求：其轴向伸缩量为20mm，转动角度最大值为7度，侧向偏移9mm。基于滑动接头的工作特性，在有限元模拟过程中将空气导管连接有滑动接头的部位释放，视其为自由端，并根据空气导管在滑动接头处偏移的位移量去校核滑动接头的补偿能力。

2.1.3 球形接头

球形接头是空气导管系统中用于热补偿和增加管道柔性的金属元件[5-6]。如图3所示，球形接头主要由波纹节、导流片和限位器组成。该部件在弯矩的作用下具有侧向转动自由度且最大偏转角度为7.5度，不具有扭转和平动自由度。球形接头的转动特性如图4所示。

球形接头在PATRAN中主要是通过多点约束和弹簧单元进行模拟。

2.1.4 法兰和阀门

法兰和阀门在空气导管系统中作为连接件使用，不具有应力补偿和位移约束的作用，在管系应力分析过程中，将法兰和阀门处视为集中质量处理[7]。

2.2 网格划分

本文采用四边形单元，利用PATRAN提供的网格划分工具生成有限元模型，计算精度较高，速度快[8]。配平系统Part 1和Part 2的节点数分别为26302、17133，单元数分别为26102、17088。

2.3 材料属性

空气导管材料为不锈钢，型号为CRES321（A312 TP321）。A312 TP321在典型温度下的材料属性如表1所示。计算过程中，其它温度点的材料属性可通过线性拟合获得。

2.4 边界条件

由于混合腔入口处的接头具有轴向、径向移动±10mm的补偿能力，因此两侧空气导管端面在设置时释放其6个自由度；而导管与气密框固定连接，因此在连接处约束6个自由度；左右两侧的鞍形卡箍释放其轴向平动自由度以及扭转自由度。管内空气温度为260℃，环境温度为20℃，管内空气工作压力为4barg。

3 计算结果

根据上述建立的有限元模型和边界条件，在NASTRAN中采用非线性静力分析求解器，以配平系统part1为例，其应力分布如图5所示。

由图5可知，配平系统Part 1在弯管处及拉杆处出现的应力最大，其中弯管处应力最大值130MPa，小于材料屈服极限149MPa（260℃）；由此可见，配平系统的part1强度满足要求。

4 应力影响因素分析

球形接头在管系中通过增加角位移来补偿管系的应力集中，由于其重量轻、无泄漏、能自我约束等特点而广泛应用在空气导管系统的补偿设计中。球形接头本身特性的不同必然会产生不同的补偿效果，引起管系不同的应力分布情况。球形接头特性参数主要有：最大转动角度、起动力矩和转动刚度。本文通过分析球形接头在各种不同的最大转动角度和起动力矩下的管系应力分布情况，来考察球形接头参数对球形接头补偿效果的影响。配平系统仅在Part1中存在3个球形接头，因此选取配平系统Part1为研究对象。最大转动角度选取范围为：5°、6°、7°、8°、9°、10°；起动力矩选取范围为：10N·m、15N·m、20N·m、25N·m、30N·m。图6为配平系统Part1的示意图，图中颜色加深部位的弯管两端设置有球形接头，在热应力作用下，球形接头通过偏转补偿该处弯管的应力集中程度。

以下分析以该弯管的最大应力值和平均应力值为研究对象，根据其受球形接头参数影响的变化规律来考察球形接头参数对球形接头补偿效果的影响。弯管段的最大应力值及平均应力值随球形接头最大转动角度和起动力矩变化的曲线如图7和图8所示。

由图7可知，弯管处的最大应力值与平均应力值随球形接头最大转动角度变化的趋势是一致的，均随最大转动角度的增大而减小，由此表明，最大转动角度越大，补偿处弯管的应力集中程度越小，球形接头对弯管的补偿作用越好。

由图8可知，弯管处的最大应力值与平均应力值随球形接头起动力矩变化的趋势是一致的，均随起动力矩的增大而增大。由此表明，起动力矩越大，弯管处的应力集中程度越强，球形接头对弯管的补偿作用越差。

5 结论

本文在分析空气导管所受到的载荷、飞机结构的约束及其对管系作用机制的基础上，建立了某型飞机空气导管的有限元模型并进行了静态应力计算分析，获得了管系的应力分析结果，并据此采用米塞斯校核标准对管系进行安全性评定。在此基础上，考察了球形接头特性参数对管系应力分布的影响。研究结果表明：球形接头最大转动角度越大，起动力矩越小，补偿效果越好，越有利于减小管系的实际应力等级。

【参考文献】

[1]C.A.R.P. Baptista， M.J.R. Barboza， A.M.L. Adib， M. Andrade， C. Otani， D.A.P. Reis.High temperature cyclic pressurization of titanium ducts for use in aircraft pneumatic systems[J].Materials&Design， 2009，30（5）：1503-1510.

[2]A.M.L. Adib， C.A.R.P. Baptista， M.J.R. Barboza， C. Haga， C.C.F. Marques.Aircraft engine bleed system tubes： Material and failure mode analysis [J].Engineering Failure Analysis， 2007，14（8）：1605-1617.

[3]范钦珊，殷雅俊.材料力学[M].北京：清华大学出版社，2008.Fan Qinshan，Yin Yajun. Material Mechanics [M]. Beijing： Tsinghua University Press， 2008（in Chinese）.

[4]陈敏，张周红.复杂管道应力分析中的支吊架布置方法[J].压力容器，2009（03）：21-25.Chen Min， Zhang Zhouhong. Study on Support and Hanger Layout of Complex Piping Stress Analysis [J].Pressure Vessel， 2009（03）：21-25（in Chinese）.

[5]严宗达，王洪礼.热应力[M].北京：高等教育出版社，1993.Yan Zongda，Wang Hongli.Thermal stress[M]. Beijing： High Education Press， 1993（in Chinese）.

[6]肖健昌.管道应力分析及热补偿在外管工程设计中的应用[J].云南化工，2000（03）.Xiao Jian-chang .Application of Pipe Stress Analysis and Thermal Compensation on the Design of Piperack Engineering [J].Yunnan Chemical Technology， 2000， （03）：26-30（in Chinese）.

[7]Chang Kyong-Ho，Jang Gab-Chul，Shin Young-Eui，etal. The behavior of welded joint in steel pipe members under monotonic and cyclic loading [J].International Journal of Pressure Vessels and Piping， 2006，03：280-298.

[8]古成中，吴新跃.有限元网格划分及发展趋势[J].计算机科学与探索，2008（03）：248-259.Gu Chengzhong； Wu Xinyue .A review of FEM and trend of development[J].Journal of Frontiers of Computer Science & Technology，2008（03）：248-259（in Chinese）.

[责任编辑：汤静]