储层不确定性建模研究进展

戴危艳，李少华，谯嘉翼，刘诗宇（.长江大学油气资源与勘探技术教育部重点实验室，武汉43000；.长江大学地球科学学院，武汉43000）

储层不确定性建模研究进展

戴危艳1，李少华2，谯嘉翼2，刘诗宇2
（1.长江大学油气资源与勘探技术教育部重点实验室，武汉430100；2.长江大学地球科学学院，武汉430100）

由于资料的不完备性及储层的非均质性，使得储层及其属性分布预测结果存在较大的不确定性。随机建模技术通过改变随机模拟路径并建立多个实现来刻画地质模型中的不确定性。储层不确定性建模是在随机建模的基础上发展起来的一项新技术，更加强调从数据获取、建模参数设置到模型响应各个阶段的不确定性表征与评价。在大量文献调研的基础上，对储层建模过程中的不确定性来源进行了分类，对储层建模中的局部不确定性、空间不确定性和响应不确定性进行了系统的阐述，并提出了一些降低不确定性的方法。现阶段储层不确定性的研究主要集中在2个方面，即不确定性评价和如何降低不确定性，而针对不确定性建模方法的研究有待进一步加强。

非均质性；随机模拟；储层地质模型；不确定性

0　引言

由于储层存在非均质性，尤其是陆相碎屑岩储层非均质性严重，使得用有限的资料来预测储层的属性存在较大的不确定性［1-3］。近年来，不确定性在油藏开发工作中备受关注，许多学者对储层建模过程中的不确定性进行了研究［4-9］。不确定性问题解决得好，储层建模的结果就会更合理，更符合地质认识，也就能更好地指导油田的开发工作［10-14］。现阶段储层不确定性的研究主要集中在2个方面，即不确定性评价和如何降低不确定性，而针对不确定性建模方法的研究则相对较少。目前常用的储层建模方法是随机建模，它利用随机模拟方法，对井间产生可选的、等概率的预测结果，从而对储层进行不确定性评价，可满足储层开发风险性分析的需要［15-16］。不确定性建模即建立表征不确定性的模型，它是在随机建模的基础上发展起来的，两者之间既相互联系，也存在差别。相对于随机建模来说，不确定性建模对不确定性的针对性更强，它能利用数学方法表征随机模拟方法所构建的储层地质模型的不确定性。因此，加强储层不确定性建模的研究，对于油气的勘探开发，尤其是非均质性严重的储层的勘探开发具有十分重要的意义。

笔者在已做研究和文献调研的基础上，详细分析储层建模过程中不确定性的来源，对储层表征中的3类不确定性及其建模方法进行系统的总结和阐述，提出一些降低不确定性的方法，以期为油田开发提供借鉴。

1　不确定性来源分析

对不确定性的来源，不同的人有不同的认识，比较系统的划分是客观世界的不确定性和认知的不确定性［17-18］。弄清储层建模过程中不确定性来源对准确预测储层内部结构至关重要，因为只有如此，才能寻求合适的方法来评价并降低不确定性带来的影响。Manceau等［19］总结出储层建模过程中不确定性来源主要有5个，即静态模型、模型粗化、数值模拟、生产数据整合以及生产方案与经济评估。Singh等［20］提出在油田开发阶段早期，不确定性来源主要有4个，即地球物理的不确定性、地质的不确定性、岩石物理特征的不确定性及动态的不确定性。吴胜和等［21］研究认为，地下储层表征中的不确定性源于资料的不完善和研究人员对储层概念模式认知的不足及分歧。Zee Ma等［22］提出造成储层建模不确定性的主要因素有油藏建模数据的质量、不同算法参数的选取以及研究者自身的理论基础和实践经验。总结不同学者对储层不确定性来源的认识可知，储层建模过程中的不确定性来源除了建模资料不完善外，还有建模软件本身的局限性、模拟算法的选取、参数的设置以及建模人员对研究区认识程度和对软件熟悉程度等因素。储层非均质性及资料的不完善会使随机模拟的结果存在多解性；建模过程中若不能选取合适的模拟算法并设置模拟参数，会使构建的静态地质模型存在不确定性；在进行油藏数值模拟之前，考虑到计算时间及成本的限制，需要对精细地质模型进行粗化，而这一过程也会产生不确定性。上述所有来源的不确定性最终将会导致储层预测结果的不确定性。

2　储层表征中的不确定性

在储层表征过程中，主要有3类不确定性：局部不确定性、空间不确定性和响应不确定性［23］。局部不确定性指未取样点处变量值的不确定性，在储层地质模型中表现为单个网格模拟值的不确定性。空间不确定性指几个点的联合不确定性，在储层地质模型中表现为多个网格模拟值的不确定性。由于储层存在非均质性，特别是陆相碎屑岩储层非均质性严重，使得用有限的资料来预测储层的属性存在很大的不确定性。在实际研究中，通常需要建立多个模型，然后从中优选出一个或几个模型进行数值模拟研究，这些模型的联合不确定性就称为空间不确定性。响应不确定性指储层预测结果的不确定性，它由转换函数造成。如在实际建模过程中，为了节省时间，通常用粗化后的静态模型进行数值模拟，但在粗化模型时针对不同的属性要选择不同的粗化算法，还要对多个参数进行数值设定，这一过程会产生较大的不确定性，特别是对于那些非均质性严重的储层，粗化后的网格不能充分体现其内部复杂的非均质性，而这种不确定性就称为响应不确定性。在这3类不确定性中，最易描述的是局部不确定性，其次是空间不确定性，而响应不确定性的描述则最为复杂。

2.1局部不确定性建模

局部不确定性建模的目的是表征模型中单个网格模拟结果的不确定性，目前主要利用累积概率分布曲线法表征这种不确定性［24］。

累积概率分布曲线法是一种数理统计方法，它是通过计算随机模拟生成的多个实现中正确的模拟结果所占的比例，来表征模型的局部不确定性。Goovaerts［25］利用序贯高斯模拟算法构建了多个三维地质模型，分别在离井较近处和离井较远处随机选取2个点u1和u2（图1，图中不同颜色的点表示渗透率值已知的井点），再从各个模型中提取出这2个点的渗透率模拟结果，进而统计分析这些值出现的频率，绘制累积概率分布图，并根据由该图得出的所有属性模拟值中正确的值所占的比例，评价了模拟结果的局部不确定性。图2（a）和图2（b）分别为u1和u2模拟结果的累积概率分布图，图中箭头所指处为实际渗透率值。u1处有约35%的模拟值与实际渗透率值接近，而u2处只有约1%的模拟值与实际渗透率值接近。造成这种情况的原因是u1离井较近，与条件数据的空间相关性较大，而u2离井较远，与条件数据的空间相关性较小，对u1进行模拟时会受到条件数据的约束，所以u1模拟结果的不确定性要小于u2。

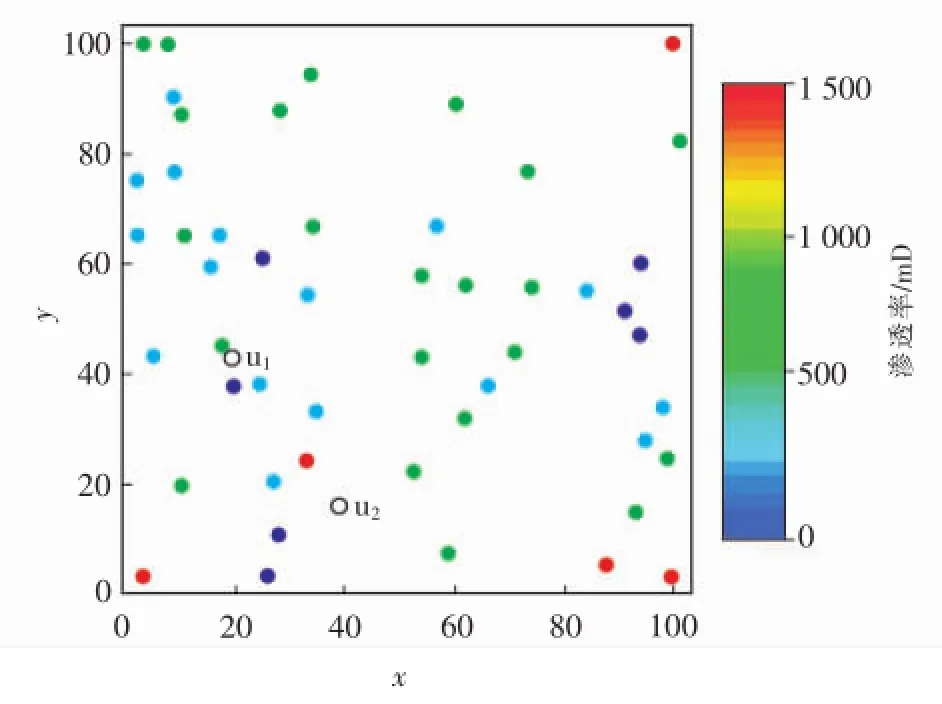
图1　取样点位置分布（据文献［25］修改）Fig.1Location of samples

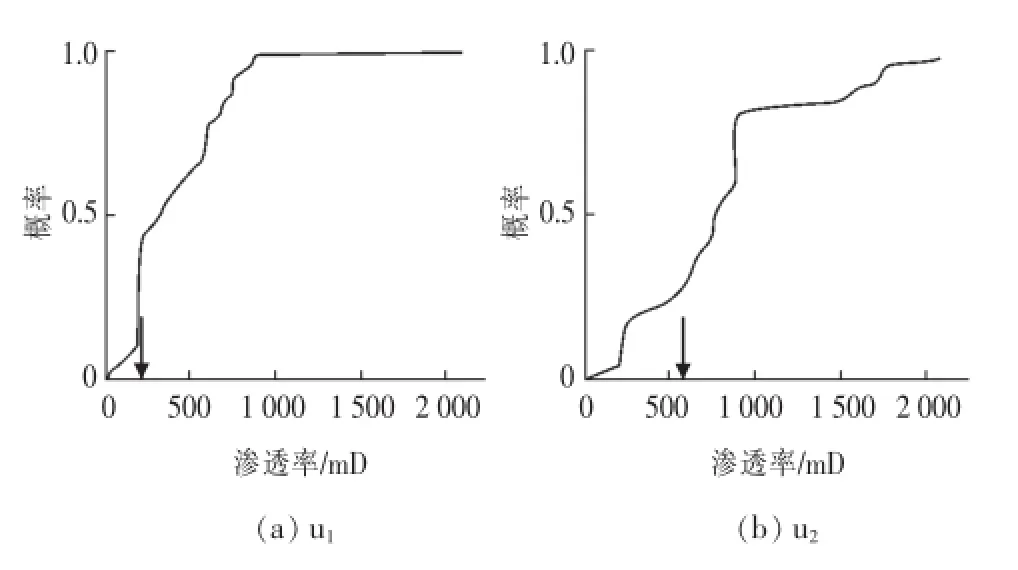
图2　累积概率分布图［25］Fig.2Cumulative probability distribution

局部不确定性、空间不确定性和响应不确定性三者相互关联，局部不确定性越大，空间不确定性和响应不确定性就越大。因此，要降低空间不确定性和响应不确定性，首先得降低局部不确定性。在井点稀少的研究区，可应用地震资料来增加横向储层分布预测的可靠程度，以降低因取样点少而带来的不确定性。地震资料在空间上提供了众多数据点作为约束条件，井资料为计算变差函数提供了准确的数据，这些都能在一定程度上降低建模过程中的不确定性。应用从构造、沉积及成岩背景相似的成熟研究区提取的资料来约束建模过程，也可降低储层建模过程中的不确定性。此外，还可通过改善算法或使用多种算法来降低建模过程中的不确定性。当然，选择合理的建模策略也很重要，许多研究人员在实际建模过程中，针对不同类型的储层采取不同的建模策略，节省了不少人力和物力。不同建模方法各有其适用条件，研究人员应了解各种建模方法的优缺点，以便合理使用。

2.2空间不确定性建模

2.2.1散点图法

散点图是度量两变量关系强弱的最直观的图形。通过观察2个网格模拟结果的散点图，可以直观地看出在2个网格上模拟结果都正确的点所占的比例，该比例越大，表示空间不确定性越小；反之，则表示空间不确定性越大。Goovaerts［26］通过绘制相同模拟条件下由同一算法建立的多个模型中2个不同网格属性模拟值的散点图，计算图中在2个网格上模拟结果都正确的点所占的比例，并据此比例值评价了模拟结果的空间不确定性（图3）。图3中箭头所指位置为实际渗透率值，越靠近2个箭头的交会点，不确定性就越小。

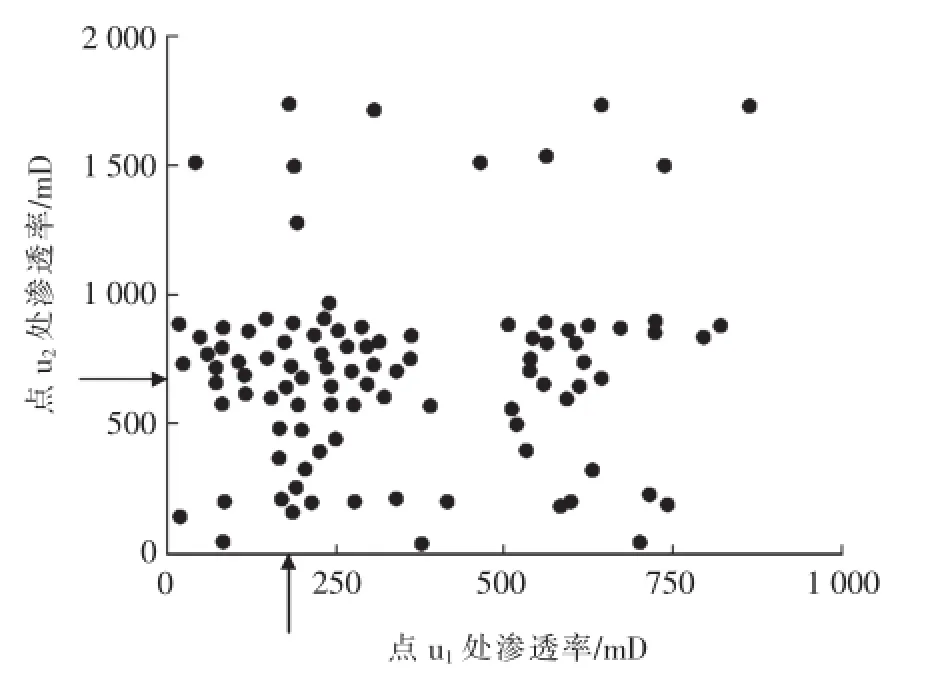
图3　点u1和u2处100个渗透率值的散点图（据文献［26］修改）Fig.3Scatter plot of 100 permeability values at u1and u2

2.2.2距离法

距离法利用距离函数计算各个模型之间的差异，然后根据差异的大小来判断模拟结果的不确定性，差异越大，不确定性就越大，差异越小，不确定性就越小。度量差异的距离函数有很多，如欧氏距离、马氏距离、切比雪肤距离、曼哈顿距离及明考斯基距离等等［27-30］。其中，最常用的是欧氏距离，也称欧几里得距离，它是在m维空间中2个点之间的真实距离。在二维和三维空间中的欧氏距离就是两点之间的距离［31-32］，其计算公式为

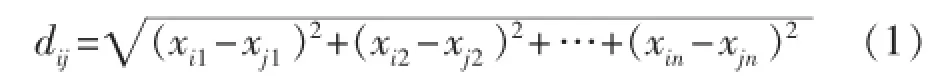
式中：i和j分别表示2个模型；n为模型网格总数；xin和xjn分别为这2个模型第n个网格的属性值，可以是渗透率或孔隙度，亦或其他一些特征值。该公式的原理是先计算2个模型相对应的每个网格属性值差的平方和，然后取平方根得到的结果，即为2个模型的欧氏距离。欧氏距离是2个模型所对应的每个网格属性模拟值差异的累加，可以用该距离函数来刻画模型的差异。

Scheidt等［33］提出利用欧氏距离来表征模拟结果的空间不确定性，即利用多个点模拟结果的差异来判断空间不确定性的大小（图4）。首先提取出各个模型中这些点的模拟值，再以这些模拟值为原数据，利用距离函数计算模型之间的差异，差异越大，表示模拟结果的空间不确定性越大。图4中δ表示模型与模型之间的差异。

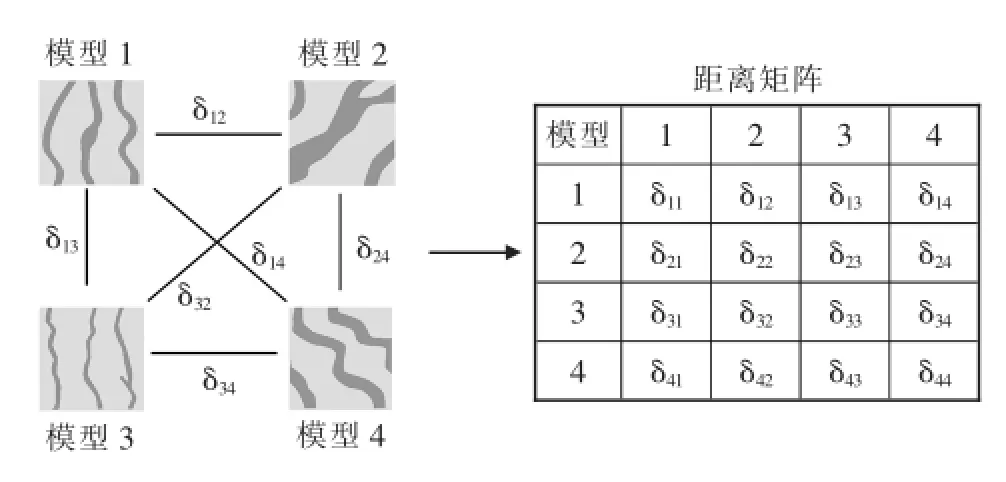
图4　欧式距离矩阵［33］Fig.4Representing spatial uncertainty of simulated results using distances

由于空间不确定性是多个点的联合不确定性，所以只要单个点模拟结果的不确定性（局部不确定性）较大，就会使得这些点模拟结果的联合不确定性较大，即空间不确定性较大。因此，要降低模拟结果的空间不确定性，首先就得降低模拟结果的局部不确定性。

上述2种空间不确定性建模方法中，散点图法表征的是各模型对2个网格模拟结果的联合不确定性，当要表征模型中2个以上网格模拟结果的联合不确定性时，该方法就不适用了，而距离法表征的是对所有网格模拟结果的联合不确定性，它能够得出各模型中所有网格模拟结果之间的差异，因而可以直观地反映模拟结果的空间不确定性。

2.3响应不确定性建模

响应不确定性建模的目的是为了研究各种不确定性因素对响应值（产油量、储量和见水时间等）的影响。目前，研究响应不确定性的方法主要有标准偏差法、方差分析法和敏感性分析法。这些方法可分别从不同角度对响应不确定性进行表征。

2.3.1标准偏差法

标准偏差反映数值相对于平均值的离散程度。标准偏差法通过计算模拟结果的标准偏差来判断不确定性因素对响应值的影响。Goovaerts［34］分别用序贯指示模拟、序贯高斯模拟、概率场模拟和模拟退火等算法建立渗透率的三维地质模型，然后在模型中随机选取一个网格，计算各算法在实现个数不同时，对该网格的模拟结果的标准偏差，并统计了随着实现个数增加，各算法模拟结果的标准偏差的变化。结果表明，当实现个数小于10时，随着实现个数的增加，模拟结果的标准偏差急剧增大，而当实现个数大于10时，标准偏差基本不再变化（图5）。这说明当随机模拟生成的实现个数较多时，其模拟结果的不确定性会降低。

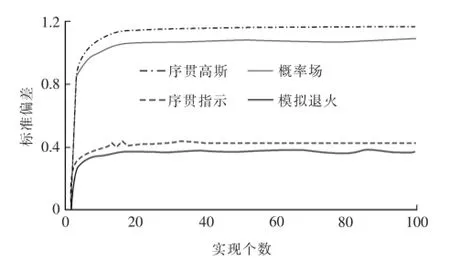
图5　实现个数和算法对模拟结果的影响［34］Fig.5Impact of simulation algorithm and number of realizations on the simulated results

2.3.2方差分析法

方差分析是统计学的一个概念，又称“变异数分析”或“F检验”，用于2个及2个以上样本均数差别的显著性检验，是一种比较不同数据间是否有明显差别的方法［35］。李少华等［36］利用方差分析得到了影响河流相储层砂体连通体积因素的重要性排序（表1）。其中，NTG和河宽对砂体连通体积的影响特别显著，井距对砂体连通体积的影响显著，曲率对砂体连通体积有影响但不显著，而宽厚比与偏离角则对砂体连通体积无影响，各影响因素的重要性依次为NTG、河宽、井距、曲率、偏离角和宽厚比。Loska等［37］通过方差分析对雷布尼克储层沉积物中重金属来源进行分析，得到了沉积物中重金属的主要来源和次要来源。Gill［38］利用方差分析对储层进行评价，取得了一定的成果。

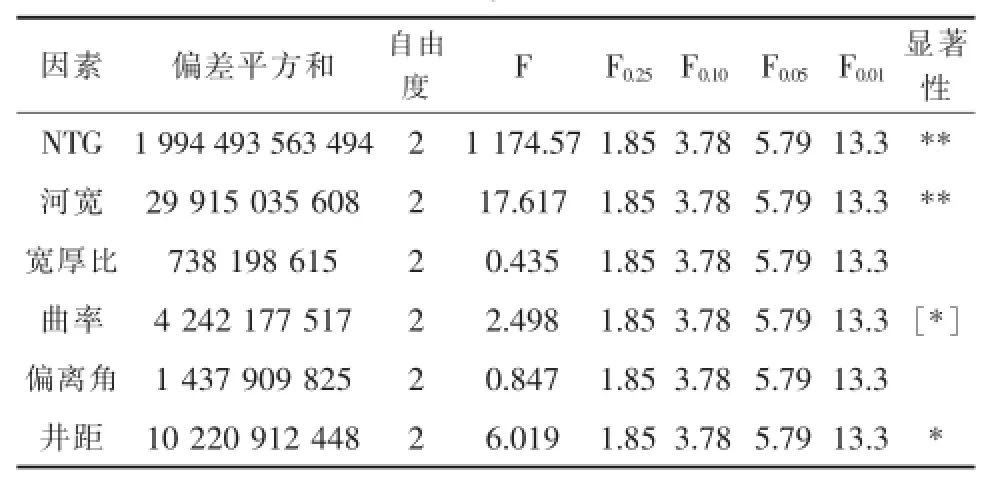
表1　方差分析［36］Table 1Analysis of variance

2.3.3敏感性分析法

敏感性分析是指从众多不确定性因素中找出对分析对象具有重要影响的敏感性因素，并分析、测算其对分析对象的影响程度和敏感性程度，是一种不确定性分析方法，已在石油地质学领域得到广泛应用［39-40］。敏感性分析主要包括以下几个步骤［41-42］：①确定分析的对象；②选定不确定性因素，并设定其变化范围；③计算不确定性因素的变化对分析对象的影响程度，并找出敏感性因素；④绘制敏感性分析图。崇仁杰等［43］通过敏感性分析对影响模型地质储量计算的不确定性因素进行了分析（图6），得出孔隙度下限的变化对模型地质储量影响最大，其次是气水界面（其值越大，模型地质储量也越大），再次是岩相体积比，而沉积微相变异函数、沉积微相体积比以及孔隙度变异函数对模型地质储量影响不大。Caers［44］利用敏感性分析方法对某油田影响累计产油量的4个不确定性参数进行了分析，得出河道厚度对产油量的影响最大，其次为河道曲折度和河道宽厚比，而砂岩含量对产油量的影响最小。Fenwick等［45］通过敏感性分析认识到相对渗透率和渗透系数对累计产油量有较大的影响。

标准偏差、方差分析和敏感性分析等方法都能对响应不确定性进行定量表征，但标准偏差法一次仅能考虑一种因素的影响，若要研究多个不确定性因素的影响，则需要做多次模拟实验，且不能给出各因素对响应值的影响程度。相比较而言，方差分析法和敏感性分析法则能同时考虑多个不确定性变量对响应值的影响，且能计算各个影响因素的重要性，因此，这2种方法在响应不确定性建模研究中更为实用。

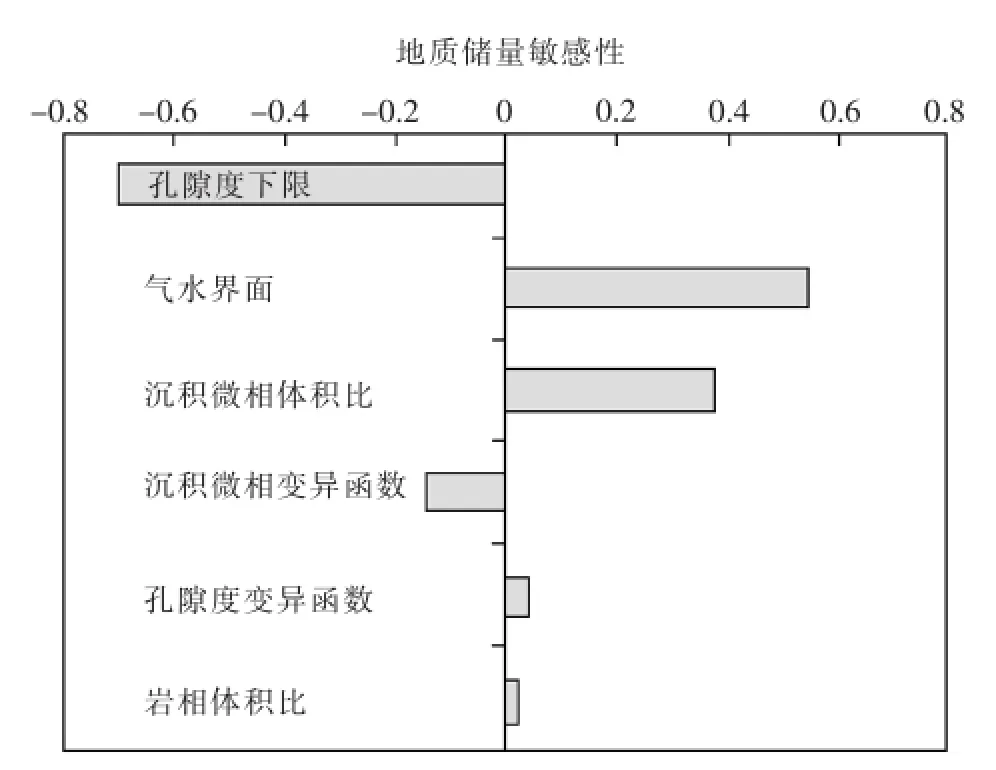
图6　地质储量敏感性分析［43］Fig.6Sensitivity analysis of geologic reserves

3　结论

（1）储层建模过程中的不确定性来源包括建模资料不完善、建模软件本身的局限性、模拟算法的选取、参数的设置以及建模人员对研究区认识程度和对软件熟悉程度等因素，其中建模资料不完善是主要影响因素。

（2）局部不确定性在储层地质模型中表现为单个网格模拟值的不确定性，可通过绘制累积概率分布曲线对其进行表征。通过分析地震数据和在相似露头区收集的资料、优化算法以及合理选择建模方法，可降低模拟结果的局部不确定性。

（3）空间不确定性在储层地质模型中表现为多个网格模拟值的不确定性，可通过欧氏距离法和绘制模拟结果散点图对其进行表征。散点图法适用于表征各模型对2个网格模拟结果的联合不确定性，而要表征模型中2个以上网格模拟结果的联合不确定性时，距离法比散点图法更实用。

（4）响应不确定性指储层预测结果的不确定性，它由转换函数造成，可通过标准偏差法、方差分析法和敏感性分析法对其进行表征。标准偏差法一次仅能考虑一种因素的影响，且不能给出各因素对响应值的影响程度，而方差分析法和敏感性分析法能同时考虑多个不确定性参数对响应值的影响，且能计算各个影响因素的重要性。方差分析法和敏感性分析法在响应不确定性建模研究中更为实用。

（5）储层不确定性建模研究对油气勘探和开发具有重要的意义，尤其是对于非均质性严重的储层，更应加强对其储层不确定性建模的重视和深入研究。目前，国内对储层不确定性的研究集中在不确定性评价和如何降低不确定性等2个方面，今后还需进一步加强对不确定性建模方法的研究。

（References）：

［1］李少华，张昌民，彭裕林，等.储层不确定性评价［J］.西安石油大学学报：自然科学版，2004，19（5）：16-19. Li Shaohua，Zhang Changmin，Peng Yulin，et al.Assessment of reservoir uncertainty［J］.Journal of Xi'an Shiyou University：Natural Sciences Edition，2004，19（5）：16-19.

［2］孙立春，高博禹，李敬功.储层地质建模参数不确定性研究方法探讨［J］.中国海上油气，2009，21（1）：35-38. Sun Lichun，Gao Boyu，Li Jinggong.A discussion on the method to study uncertainty of geologic modeling parameters［J］.China Offshore Oil and Gas，2009，21（1）：35-38.

［3］Oberkampf W L，de Land S M，Rutherford B M，et al.Error and uncertainty in modeling and simulation［J］.Reliability Engineering& System Safety，2002，75（3）：333-357.

［4］Bárdossy G，Fodor J.Evaluation of uncertainties and risks in geology：New mathematical approaches for their handling［M］.Germany：Springer，2013.

［5］霍春亮，刘松，古莉，等.一种定量评价储集层地质模型不确定性的方法［J］.石油勘探与开发，2007，34（5）：574-579. Huo Chunliang，Liu Song，Gu Li，et al.A quantitative method for assessing uncertainty of the reservoir geological model［J］.Petroleum Exploration and Development，2007，34（5）：574-579.

［6］Zafari M，Reynolds A C.Assessing the uncertainty in reservoir description and performance predictions with the ensemble Kalman filter［J］.SPE Journal，2007，12（3）：382-391.

［7］Smalley P C.Handling risk and uncertainty in petroleum exploration and asset management［J］.AAPG Bulletin，2008，92（10）：1251-1261.

［8］Maschio C，de Carvalho C P V，Schiozer D J.A new methodology to reduce uncertainties in reservoir simulation models using observed data and sampling techniques［J］.Journal of Petroleum Science and Engineering，2010，72（1）：110-119.

［9］Armstrong M，Ndiaye A，Razanatsimba R，et al.A scenario reduction applied to geostatistical simulations［J］.Mathematical Geosciences，2013，45（2）：165-182.

［10］薛艳霞，廖新武，赵春明，等.基于随机建模技术的油田开发初期河流相储层不确定性分析方法——以渤海A油田为例［J］.岩性油气藏，2012，24（1）：80-83. Xue Yanxia，Liao Xinwu，Zhao Chunming，et al.Uncertainty analysis of fluvial reservoir in oilfield early development period based on stochastic modeling：A case study from A oilfield in Bohai Bay［J］.Lithologic Reservoirs，2012，24（1）：80-83.

［11］罗文生，孙立春，郑洪印，等.蒙特卡罗法在海上某油田储量评价中的应用［J］.岩性油气藏，2014，26（1）：105-109. Luo Wensheng，Sun Lichun，Zheng Hongyin，et al.Application of Monte-Carlo method to OOIP estimation of an offshore oilfield［J］. Lithologic Reservoirs，2014，26（1）：105-109.

［12］Srivastava R M.The visualization of spatial uncertainty［J］.AAPG Computer Applications in Geology，1994（3）：339-345.

［13］Kupfersberger H，Deutsch C V.Ranking stochastic realizations for improved aquifer response uncertainty assessment［J］.Journal of Hydrology，1999，223（1）：54-65.

［14］张婷，徐守余.储层地质建模技术研究与展望［J］.长春理工大学学报：高教版，2009，4（4）：191-192. Zhang Ting，Xu Shouyu.Research and prospect of reservoir geologic modeling technology［J］.Journal of Changchun University of Science and Technology，2009，4（4）：191-192.

［15］于兴河.油气储层表征与随机建模的发展历程及展望［J］.地学前缘，2008，15（1）：1-15. Yu Xinghe.A review of development course and prospect of petroleum reservoir characterization and stochastic modeling［J］.Earth Science Frontiers，2008，15（1）：1-15.

［16］苏进昌，张岚，马新福.河流相储层开发初期地质建模［J］.岩性油气藏，2008，20（3）：114-118. Su Jinchang，Zhang Lan，Ma Xinfu.Geological modeling in initial stage of development of fluvial reservoir［J］.Lithologic reservoirs，2008，20（3）：114-118.

［17］McVay D A，Lee W J，Alvarado M G.Calibration improves uncertainty quantification in production forecasting［J］.Petroleum Geoscience，2005，11（3）：195-202.

［18］Floris F J T，Bush M D，Cuypers M，et al.Methods for quantifying the uncertainty of production forecasts：A comparative study［J］. Petroleum Geoscience，2001，7（S1）：S87-S96.

［19］Mezghani I Z，Manceau E，Feraille M.Uncertainty management：From geological scenarios to production scheme optimization［J］. JournalofPetroleumScienceandEngineering，2004，44（1）：11-25.

［20］Singh V，Hegazy M，Fontanelli L.Assessment of reservoir uncertainties for development evaluation and risk analysis［J］.The Leading Edge，2009，28（3）：272-282.

［21］吴胜和，杨延强.地下储层表征的不确定性及科学思维方法［J］.地球科学与环境学报，2012，34（2）：72-80. Wu Shenghe，Yang Yanqiang.The uncertainty and scientific thinking method of reservoir characterization［J］.Journal of Earth Science and Environment，2012，34（2）：72-80.

［22］Zee Ma Y，La Pointe P.Uncertainty Analysis and Reservoir Modeling［M］.American：AAPG，2011.

［23］Goovaerts P.Geostatistical modeling of the spaces of local，spatial，and response uncertainty for continuous petrophysical properties［J］.AAPG Computer Applications in Geology，2006（5）：59-79.

［24］Goovaerts P.AUTO-IK：A 2D indicator kriging program for the automated non-parametric modeling of local uncertainty in earth sciences［J］.Computers&geosciences，2009，35（6）：1255-1270.

［25］Goovaerts P.Impact of the simulation algorithm，magnitude of ergodic fluctuations and number of realizations on the spaces of uncertainty of flow properties［J］.Stochastic Environmental Research and Risk Assessment，1999（13）：161-182.

［26］Goovaerts P.Geostatistical modelling of uncertainty in soil science［J］.Geoderma，2001，103（1）：3-26.

［27］Groenen P J F，Jajuga K.Fuzzy clustering with squared Minkowski distances［J］.Fuzzy Sets and Systems，2001，120（2）：227-237.

［28］de Maesschalck R，Jouan-Rimbaud D，Massart D L.The mahalanobis distance［J］.Chemometrics and intelligent laboratory systems，2000，50（1）：1-18.

［29］Sim D G，Kwon O K，Park R H．Object matching algorithm using robust Hausdorff distance measures［J］．IEEE Trans．Image Process，1999，8（2）：425-429．

［30］Rote G.Computing the minimum Hausdorff distance between two point sets on a line under translation［J］．Information Process Letters，1991，38：123-127．

［31］贺玲，吴玲达，蔡益朝.高维空间中数据的相似性度量［J］.数学的实践与认识，2006，36（9）：189-194. He Ling，Wu Lingda，Cai Yichao.Similarity measurement of data in high dimensional spaces［J］.Journal of Mathematics in Practice and Theory，2006，36（9）：189-194.

［32］Carter R L，Morris R，Blashfield R K.On the partitioning of squared Euclidean distance and its applications in cluster analysis［J］.Psychometrika，1989，54（1）：9-23.

［33］Scheidt C，Caers J.Representing spatial uncertainty using distances and kernels［J］.Mathematical Geosciences，2009，41（4）：397-419.

［34］Goovaerts P.Geostatistical modelling of spatial uncertainty using p-field simulation with conditional probability fields［J］.International Journal of Geographical Information Science，2002，16（2）：167-178.

［35］吕栋雷，曹志耀，邓宝，等.利用方差分析法进行模型验证［J］.计算机仿真，2006，23（8）：46-48. Lü Donglei，Cao Zhiyao，Deng Bao，et al.Application of variance analysis in model validation［J］.Computer Simulation，2006，23（8）：46-48.

［36］李少华，李强，李君.影响砂体连通体积因素的定量评价［J］.天然气地球科学，2014，25（5）：643-648. Li Shaohua，Li Qiang，Li Jun.Quantitative evaluation of the factors controlling the sand body connected volumes［J］.Natural Gas Geoscience，2014，25（5）：643-648.

［37］Loska K，Wiechula D.Application of principal component analysis for the estimation of source of heavy metal contamination in surface sediments from the Rybnik Reservoir［J］.Chemosphere，2003，51（8）：723-733.

［38］Gill D.Application of a statistical zonation method to reservoir evaluation and digitized-log analysis［J］.AAPG Bulletin，1970，54（5）：719-729.

［39］马功联.断块油藏特高含水期水驱开发因素敏感性分析［J］.海洋石油，2005，25（1）：46-49. Ma Gonglian.Sensitivity analysis of waterflooding development factors in extra high water cut period of fault block reservoirs［J］. Offshore Oil，2005，25（1）：46-49.

［40］赵静，赵泉.低渗透分支井井网产能预测及参数敏感性分析［J］.西南石油大学学报：自然科学版，2010，32（1）：112-116. Zhao Jing，Zhao Quan.Deliverability for recast for multi-lateral well pattern and parameter sensitivity research in low-permeability reservoirs［J］.Journal of Southwest Petroleum University：science&Technology Edition，2010，32（1）：112-116.

［41］Oakley J E，O'Hagan A.Probabilistic sensitivity analysis of complex models：A Bayesian approach［J］.Journal of the Royal Statistical Society：Series B（Statistical Methodology），2004，66（3）：751-769.

［42］Van Griensven A，Meixner T，Grunwald S，et al.A global sensitivity analysis tool for the parameters of multi-variable catchment models［J］.Journal of hydrology，2006，324（1）：10-23.

［43］崇仁杰，于兴河，李婷婷.应用实验设计优选随机建模的储层模型［J］.石油与天然气地质，2012，33（1）：94-100. Chong Renjie，Yu Xinghe，Li Tingting.Selecting reservoir model built by stochastic modeling through experimental design［J］.Oil and Gas Geology，2012，33（1）：94-100.

［44］Caers J.Modeling Uncertainty in the Earth Sciences［M］.Chichester：Wiley Blackwell，2011.

［45］Fenwick D，Scheidt C，Caers J.Quantifying asymmetric parameter interactions in sensitivity analysis：Application to reservoir modeling［J］.Mathematical Geosciences，2014，46（4）：493-511.

（本文编辑：于惠宇）

Progress of reservoir uncertainty modeling

Dai Weiyan1，Li Shaohua2，Qiao Jiayi2，Liu Shiyu2
（1.Key Laboratory of Exploration Technologies for Oil and Gas Resources，Ministry of Education，Yangtze University，Wuhan 430100，China；2.School of geosciences，Yangtze University，Wuhan 430010，China）

Due to the incomplete information and reservoir heterogeneity，it is unable to accurately determine the distribution of reservoir and its properties.Stochastic modeling technique can characterize the uncertainty of geologic model by generate multiple realizations through changing the stochastic simulation path.Reservoir uncertainty modeling is a new technology developed on the basis of the stochastic modeling，and it paid more emphasis on the characterization and evaluation of uncertainty that resulted from data acquisition，modeling parameter and response of models.Based on a large number of relevant references，this paper classified the sources of uncertainty in the process of reservoir modeling，expounded the local uncertainty，spatial uncertainty and response uncertainty in reservoir modeling，and put forward some methods to reduce the uncertainty.The research of the reservoir uncertainty mainly focused on the aspects of uncertainty evaluation and uncertainty reduction at present，and the research of uncertainty modeling methods should be strengthen.

heterogeneity；stochastic simulation；reservoir geologic model；uncertainty

TE121.1+5

A

1673-8926（2015）04-0127-07

2014-12-10；

2015-02-22

国家自然科学基金项目“点坝砂体内部非均质性的层次建模法”（编号：41272136）和非常规油气湖北省协同中心创新基金项目“页岩气储量计算的概率体积法”（编号：HBUOG-2014-14）联合资助

戴危艳（1991-），女，长江大学在读硕士研究生，研究方向为地质建模和油藏描述。地址：（430100）湖北省武汉市蔡甸区大学路特1号长江大学地球科学学院。E-mail：879573435@qq.com

李少华（1972-），男，教授，博士生导师，主要从事地质统计学、地质建模方面的研究与教学工作。E-mail：jpishli@163.com。