双层规划模型在高校图书馆投资中的应用
2015-09-26石彩英
石彩英,陈 源
(1.衡阳师范学院图书馆,衡阳湖南 421002;2.衡阳师范学院数学与统计学院,衡阳湖南 421002)
双层规划模型在高校图书馆投资中的应用
石彩英1,陈源2
(1.衡阳师范学院图书馆,衡阳湖南 421002;2.衡阳师范学院数学与统计学院,衡阳湖南 421002)
高校图书馆投资具有 “双层”的特点,利用双层规划模型研究高校图书馆投资问题具有重要意义。该文分析了重点专业优先发展的策略下高校图书馆最优投资的层次与步骤,建立了重点专业优先发展的最优投资双层规划模型,给出了上、下两层最优投资方案的确定方法。
重点专业;高校图书馆;最优投资;双层规划模型
0 引言
高校图书馆投资,是指在一定时期内投入到高校图书馆的人力、财力和物力的总和[1]。高校图书馆针对各学科专业的投资主要有以下方面:纸质文献的投资、电子文献的投资、精品课网的投资、图书馆员的投资。所谓重点专业,就是重点建设的专业或重点发展的专业,是专业主体根据社会发展的需要和专业自身发展的规律和实际,采取各种措施和手段促进专业发展和专业水平提高的一种社会实践活动[2]。高校的重点专业是指经过充分认证和评估而确立的,旨在为高校自身办学确定目标和品牌特色,这样才能够找到高校自身发展的方向和坐标。图书馆的建设是学校建设发展的推动器,而重点专业的建设是学校发展的发动机,因此,图书馆的发展和重点专业的建设对高校的发展起到重要的作用。
部分高校由于受过去计划经济的影响,专业文献配置上简单地搞平均主义。这样做的主要原因有两个方面:一方面是为了好体现公平公正的原则,减少图书馆与系科间的矛盾,另一方面是经费配置单一,避免操作繁琐。看似比较公平也少了不少麻烦,但是这样做对高校的建设和发展毫无益处:高校馆藏结构无重点、主次之分,学校既没有对重点专业、特色专业、特殊专业的文献进行应有的加强,也没有对边缘科学、新兴科学等的文献进行必要的补充,学校对一些时效性强、半衰期短的专业文献(如计算机科学、应用电子、精细化工、现代生物技术、临床药学等文献老化淘汰快)既没有提供更多的经费也没有及时进行补充更新。所以,高校图书馆在进行投资时应综合考虑,制定符合具有本校特色的投资计划[3]。
具体做法如下:首先高校必须全面摸清其设置专业和重点专业以及馆藏文献,根据这些专业发展所必须使用的文献、主要参考文献的类别、品种、数量、文种等内容来决定各专业的经费投入比例,对优先发展的重点专业进行投资。其次高校必须在入藏文献专业系统性和完善性得到保障的前提下,用科学的方法(如文献计量法),筛选老化文献,让资金向重点专业、地方特色专业和扩招后新组合新设置专业倾斜,做好吐故纳新工作,满足新增专业的文献需求。最后用剩余资金对所有专业进行无差别投资。
高校图书馆如何进行投资决策,事实上,我们参照1994年Luis N.Vicente给出的一般双层规划模型BP(Bilevel programming)[4]。据我们研究,高校图书馆投资也具有“双层”的特点,上层为高校决策层,下层为各专业内部,以下我们建立在优先发展重点专业策略下高校图书馆最优投资双层规划模型。
1 模型的建立
1.1提出问题
某高校有s个专业,其中重点专业有m个(m<s),经过预算,高校用于高校图书馆的投资总量为Q,假设对每个重点专业的投资额度为xi(i=1,2,…,m)。每专业有n个方面需要投资,由于专业不同,所需的学习、科研资源也不尽相同,因此每招收一位学生所需的方面投资也就不会相同。为保证高校图书馆质量,要求每个专业必须满足基本生均办学条件,基本条件不达标者不可超招学生。由于重点专业是国家大量需要专业人才的专业,假设要求重点专业的在校生人数不少于Qi。
设第i专业每增加一名学生在第j方面需投入的费用为aij(i=1,2,…,s,j=1,…,n),Nij为专业i当前第j方面资源保有量(以该项资源所能够负担学生数量表示),xij为第i专业计划对第j方面资源的投资额(以j方面资源最多可以负担在校生的数量表示)。问高校图书馆如何分配资金Q,才能保证在重点专业优先发展的前提下,为高校的建设作出最大的贡献。
1.2高校图书馆投资决策的层次
上层为图书馆对s个专业的投资决策xi(i=1,…,s),图书馆可分配资金总量为Q,记修第i专业的学生数量为N(xi),则应满足:

下层为专业自身内部投资,各专业自身内部对高校领导决策层分配下来的投资xi(i=1,…,s)拥有二次投资的自主分配权,通过制定对自身合适的投资计划,以最大限度地扩大本专业在校生容量,从而提高本专业在高校中的整体地位。第i专业可用于改善办学条件的资金为xi,应满足:

对于下层第i专业内部来说,它必须合理使用高校决策层分配下来的资金,使得本专业在校生容量达到最大。第i专业在校生容量取决于它的办学资源中最少的资源,第i专业的目标函数为

对于高校领导决策者而言,它的目的是保证重点专业优先发展前提下在校生总容量达到最大,因而它的目标函数为:

1.3优先发展重点专业策略下的高校图书馆最优投资决策过程
保证m类重点专业优先发展的投资,在满足重点专业投资的基本规模Qi(i=1,…,m)后,再充分利用剩余资金以追求在校生总容量最大为目的,对高校所有专业进行无差别投资,具体投资过程如下:
首先,对重点专业的发展进行优先投资:
先保证m类优先发展专业资源所能负担的在校生总量分别达到Qi(i=1,…,m),其目的是为了保证优先发展重点专业基本在校生规模的投资额度最少,尽可能多地把留有的资金进行下一步投资。分别对m类优先发展重点专业建立如下个m数学规划模型:

其次,为了达到使所有专业按在校生人数最大的目的,高校应该把剩余资金对所有专业进行无差别投资:
假设求解规划模型(1)得到最优解x1,…,xm;y11,…,y1n,…,y1m,…,ymn,保证m类优先发展重点专业基本在校生规模Qi(i=1,,…,m)后,剩余资金数量为,此时优先发展专业i当前资源拥有量变为

对高校所有专业i=1,…,s,再按以下方法对当前资源拥有量重新赋值:

用剩余资金对该高校所有专业进行无差别投资,目的是使在校生总容量最大,建立如下的数学规划模型:

2 图书馆最优投资方案的确定
假设求解模型(1)得到最优解为

求解模型(2)得到最优解为
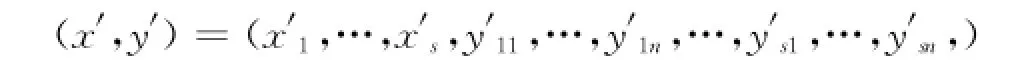
对于任意的第i专业(i=1,…,s),分以下情况确定其最优投资方案:
(1)如果1≤i≤m,此时假设第i专业在解(1)中的决策分量为(xi;xi1,…,xin),在解(2)中的决策分量为(x′i;x′i1,…,x′in),则得到第i专业的最优投资方案为(xi+x′i;ai1(xi1+x′ij),…,ain(xin+ x′in)),其中(xi+x′i)为高校图书馆对第i专业的最优投资额,aij(xji+x′ij)(j=1,…,n)为第i专业对第j方面的第二次最优投资额。
(2)如果m+1≤i≤s,此时不妨设第i专业在解(2)中的决策分量为(x′i;x′i1,…,x′in),则得到第i专业的最优投资方案为(x′i;ai1x′i1,…,ainx′in),其中x′i为高校图书馆对第i专业的最优投资额,aijx′ij(j=1,…,n)为第i专业对第j方面的第二次最优投资额。于是该高校在重点专业优先发展的投资方案前提之下即可得到总投资额为Q的最大在校生容量。
3 模型转换
引进新的变量ti,令ti≤Nij+xij,(i=1,…,m;j=1,…,n.),则(1)可转化为以下的线性规划问题:

令ti≥N′ij+xij,(i=1,…,m;j=1,…,n.),则(2)可转化为以下的线性规划问题:

运用单纯形的方法即可求解模型(1′)和(2′).
4 结语
重点专业优先发展的高校图书馆最优投资双层规划模型,不仅适用于对一般的本科院校图书馆的投资决策,而且还适用于对职业院校图书馆和其他地方图书馆等的投资决策,可以说,本模型对一般的较大型的图书馆的投资决策均有普遍的借鉴作用。
[1]全昌淑,金海燕.高校图书馆投资问题初探[J].科技情报开发与经济,2010,20(27):34-35.
[2]罗云.论大学专业建设[J].高等教育研究,2005(7):45-50.
[3]杨海鸥,王智群.西部地区地方性高校图书馆经费投入及配置合理化研究[J].四川图书馆学报,2005(2):6-9.
[4]Luis N,Vicente.Bilevel and multilevel programming:a bibliography review[J].Journal of Global Optimization,1994,5:291-306.
Application of Bi-level Programming Model in University Library Investment
SHI Cai-ying1,CHEN Yuan2
(1.Library of Hengyang Normal University,Hengyang Hunan 421002,China;2.College of Mathematics and Statistics,Hengyang Normal University,Hengyang,Hunan 421002,China)
The investment of the university library has the characteristics of“bi-level”and it has significant meaning in studying the investment of the university library by using the bi-level programming model.This paper analyzed the level and step of the most priority investment in the university library under the policy of priority development of the key specialties,established a bi-level programming model and gave a determined method of the upper and lower layers optimal investment program.
key specialty;university library;optimal investment;bi-level programming model
G255.2,O221.1
A
1673-0313(2015)06-0035-03
2015-04-16
湖南省高校图工委科研项目(2013L014);湖南省“十二五”重点建设学科资助项目(湘教发[2011]76号)
石彩英(1971-)女,湖南祁东人,馆员,研究方向:图书管理。
