基于RANSAC策略优化的稀疏矩阵指纹匹配算法
2015-09-26曹中琰施琳琳卢恩雪陈思达李全彬江苏省先进激光材料与器件重点实验室江苏师范大学物理与电子工程学院徐州221116
曹中琰,施琳琳,卢恩雪,陈思达,李全彬(江苏省先进激光材料与器件重点实验室,江苏师范大学物理与电子工程学院,徐州 221116)
基于RANSAC策略优化的稀疏矩阵指纹匹配算法
曹中琰,施琳琳,卢恩雪,陈思达,李全彬
(江苏省先进激光材料与器件重点实验室,江苏师范大学物理与电子工程学院,徐州221116)
0 引言
指纹识别技术是生物识别技术中最重要﹑应用最广泛的技术,具有易采集性、唯一性的突出特点。例如很多大型企事业单位已经用指纹考勤代替了传统的IC卡、磁卡等考勤方式,从而有效地提升了单位的管理效率,从根本上避免了代打考勤的现象。
指纹匹配算法是自动指纹识别系统的重要研究内容,准确且快速地提高指纹匹配算法是研究的一大热点。但是指纹数字图像识别技术仍面临着很多问题,如识别速度慢,识别成本较高,系统昂贵,系统鲁棒性差,识别错误率较高等问题,特别是采集指纹的过程中,诸如局部形变、光照条件变化、部分遮挡等因素常常导致同一指纹在不同的图像中具有较大的差异,这些都是指纹图像匹配所需要解决的难点[1]。
为了解决现有指纹匹配算法在匹配速度与准确率难以统一的问题,本文提出了基于RANSAC策略优化的稀疏矩阵的指纹匹配算法。
1 指纹匹配算法研究现状
目前,常用的指纹匹配算法主要分为三种:基于点模式的匹配方法,基于全局结构特征的匹配方法,基于融合特征的匹配方法。其中,以点模式匹配方法研究最多,应用最为广泛。Ranade和Rosenfeld利用松弛法进行特征点匹配[2]。Ratha等提出一种基于点模式的匹配,用一般的Hough变换来恢复两幅指印间的位置变换。Jiang等使用定义在局部结构特征间的相似度衡量方法以此来比对两个模式,而后得到两个细节点序列间的匹配分数。Wahab等提出一种利用细节点组来定义局部结构特征的方法。王伟希等提出了一种由指纹参考点和参考方向构成极坐标系,用极坐标表示指纹特征信息的新的点模式匹配算法[3]。曹国等通过一系列实验得出一种快速指纹混合匹配方法。首先我们应该定位指纹的中心点及其方向,然后提取指纹的图像特征并建立指纹细节点匹配模板,最终应用多级匹配的方法实现了指纹识别[4]。
除了点模式匹配法以外,在全局结构特征匹配方法上,Chen和Sherlock都分别对指纹的拓扑结构进行了研究,基于这些信息进行匹配,得以改善指纹图像的噪声、旋转和变形对识别的干扰。Tan和Bhanu提出作用于遗传算法的指纹匹配方法,利用了指纹的整体结构信息来寻找不同指纹间的最优变换。在融合匹配算法上,如Prabhakar等人提出基于决策层的融合算法,融合四种匹配算法,在一定程度上提高匹配准确率[5]。
2 稀疏矩阵指纹匹配算法
如果一个矩阵的非零元素相当少,远远小于其零元素的数量,而且该矩阵中的非零元素杂乱无章的分布在整个矩阵中,那么该矩阵就是稀疏矩阵。得益于稀疏矩阵计算速度快、存储容量较小的优点,采用稀疏矩阵可以改善指纹匹配速度。也即通过矩阵分解,取得加强指纹局部化特征的效果。
为了找到恰当的基对矩阵进行分解,本文假设已知非负矩阵V找到适合的非负矩阵因子W与H,确保V≈WH。附加定义U=[uij]=WTW,V=[vij]=HTH然后增加以下3个稀疏性限制条件:
(1)使H最大稀疏化。H必须包括尽可能多的零元素,使W的列向量更富于表现局部特征的能力;
(2)最大化W的局部表现能力。如约束1所述,H的稀疏化和W的局部化能力是息息相关的。这里进一步加强了约束1中的最大稀疏化。当且仅当∑ivij=max时局部表现能力最强;
(3)最大化W的正交性。加约束条件∑i≠juij=min,和约束1比较后,改为∑∀i,juij=min。
将上述3个约束合并起来,就可以建立如下的目标函数:
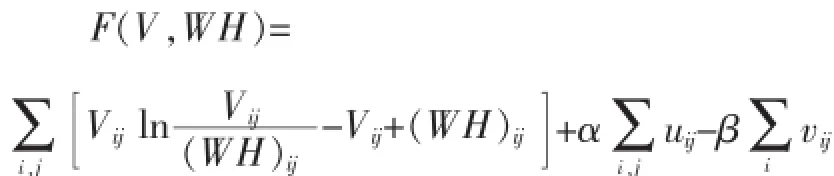
其中,α,β是大于零的常数,最小化算法可以消除它们。通过迭代计算可以得到目标函数的结果。由迭代规则可知,F(X,WH)为非增序列函数,满足收敛到局部最小点这一要求,其收敛性可以证明。非负矩阵分解的方法在处理数据时,并不假设矩阵V具有稀疏性,但是得到的分解结果具有稀疏性,然后利用分解结果稀疏的特点进行存储。本方法多用于进行矩阵数据的预处理[6]。
稀疏矩阵匹配算法更加注重指纹图像的局部特征,由于局部范围内指纹形变的可控性,因此可以很好地解决指纹图像的形变问题。但同样由于仅对局部特征进行匹配,容易造成总体误匹配率升高。
3 基于RANSAC优化的指纹匹配算法
为了提高匹配准确率,本文通过RANSAC策略进一步优化稀疏矩阵算法。在运用稀疏矩阵匹配算法进行初匹配的基础上,通过RANSAC策略进一步剔除误匹配特征点,从而提高整体算法准确率。
RANSAC策略依据一组含有异常数据的样本数据集,计算得出有效数据的数学模型参数,最终得出有效样本数据的算法,在1981年由Fishchler和Bolles第一次提出[7]。RANSAC算法的基本思路如下:
(1)从已有样本集P中选定最小需求的数据样本,并使用最小数据样本求出初始模型;
(2)通过初始模型求取问题的约束条件,当数据样本符合解的约束条件,则称其为内点,否则称为外点;
(3)如果内点的数目大于等于设定的阈值,则用内点数重新估计模型参数并结束本轮运算;如果内点的数目小于设定的阈值,则重新在数据集中选取数据样本,重复上述的步骤;
(4)经过N次采样,选取包含内点数目最多的模型,并使用这些内点重新计算模型的参数,完成计算。
在通过稀疏矩阵指纹匹配算法进行初匹配之后,减少了总体匹配所需要的特征点。RANSAC算法具有良好的鲁棒性,能够稳定地提取正确的匹配点对,消除误匹配点对。
本文RANSAC匹配算法的具体步骤如下:
(1)将初匹配得到的匹配点对作为初始数据集,要将初匹配中的误匹配点对去除。
(2)对输入指纹特征点集进行平移、旋转、尺度变换,将初匹配得到的匹配点对用直线连接起来,并计算线段与水平方向的夹角α(i),以及匹配点对方向的夹角β(i),分别对α(i)和β(i)进行统计,将最大的统计值设定为αM和βM的标准值,将α(i)和β(i)分别与αM和βM进行比较,如果误差在±3°范围内,则判定连线平行,这两对匹配点划分为内点,否则为外点;
(3)如果得到的匹配点对数目大于设定的阈值(本文采用初始匹配点数目的85%作为阈值),则保留本次计算结果。结束计算,使用内点重新估计指纹的变换参数;否则,重复上面步骤;
(4)经过N次采样,得到N个内点集,从中选取内点数目最多的一次采样,使用最小二乘法对内点集进行估计,并代入变换公式,求出变换参数,然后再进行一次整体匹配过程,得出最后的匹配点数。当匹配点数大于设定的阈值,判定两个指纹匹配,否则断定不匹配。具体算法流程图如图1所示:
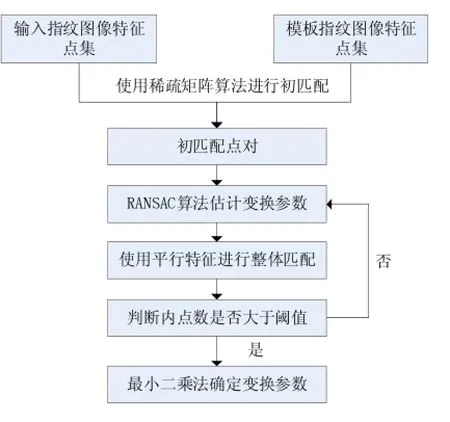
图1 总体算法流程图
4 算法结果及分析
评价算法准确率的主要指标为误识率(FAR)和拒识率(FFR)。EER代表误识率和拒识率相等时的值,EER越小,代表指纹匹配算法的准确性越高。
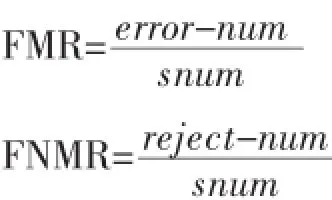
其中error-num表示不该匹配但匹配的次数,reject-num表示该匹配却没有匹配的次数,snum表示匹配的总次数。
利用FVC2004指纹数据库对本文算法进行测试,整个指纹数据库中共计100枚指纹图像[9]。算法1为文献[5]所用的指纹匹配算法,算法2为未用RANSAC策略进行优化的稀疏矩阵匹配算法,算法3为本文所用算法。表1为从数据库中提取10枚指纹图像进行测试时,三种算法的表现能力。表2为本文所用算法和未进行优化的稀疏矩阵匹配算法在进行不同数量指纹图像匹配时,在准确率和匹配速度方面进行的比较。

表1 本文算法和其他算法效果比较
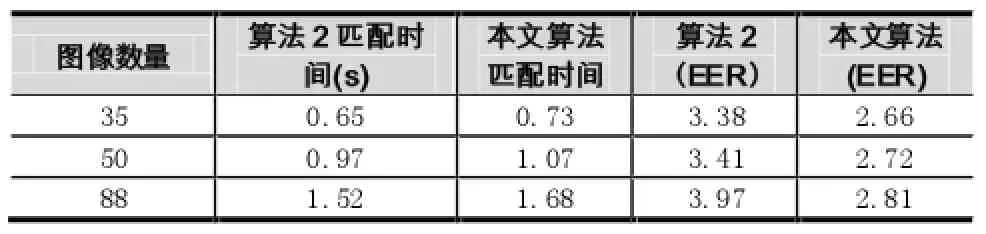
表2 本文算法和其他算法的实验测试结果比较
从表1可知,本文所使用算法与算法1相比,无论是匹配速度还是匹配精度上都有一定提高。从表2中可以看出,本文所提出的算法在匹配准确率方面有较好表现,同时并未影响算法匹配速度。
5 结语
本文所采用的基于策略优化的稀疏矩阵指纹匹配算法,在不影响匹配速度的情况下,有效提高了系统的匹配准确率。本文为了保证匹配速度,并没有设置很高的阈值,基于RANSAC算法对于迭代次数的要求,在设置更高阈值的情况下,准确率将会有进一步提高。
[1]刘舒,于瑞华.生物特征识别中的关键技术与发展趋势[J].中国人民公安大学学报:自然科学版,2006,47(1):63-65.
[2]Fischler,M.A.,Bolles,R.C.Random sample consensus:A paradigm for model fitting with applications to image analysis and automated cartography.Communications of the ACM,1981,24(6):381-395.
[3]王伟希,袁杰,臧炅.基于局部特征的点模式指纹匹配算法[J].南京大学学报:自然科学版,2009,45:18-23
[4]曹国,毛志红,梅园.快速的多级指纹混合匹配方法[J].模式识别与人工智能,2009,22:787-793
[5]于明,皮海龙,王岩.基于k近邻法和脊线追踪的指纹匹配算法[J].吉林大学学报:工学版,2014,44:1806-1810
[6]石光明,刘丹华,高大化等.压缩感知理论及其研究进展[J].电子学报,2009,37:1070-1081
[7]Wan,Dingrui,Zhou,Jie.Fingerprint recognition using model-based density map.IEEE Transactions on Image Processing,2006
[8]Cappelli R,Ferrara M,Maltoni D.Fingerprint Verification Competition at IJCB 2011.Biometrics[C].2011 International Joint Conference on Digital Object Identifier,2011,11(10):1-6
[9]Jain A K,Prabhakar S,Hong L,et al.Filterbank-based fingerprint matching.IEEE Transactions on Image Processing,2000
Fingerprint Matching;Sparse Matrix;Random Sample Consensus Strategy
Sparse Matrix Fingerprint Matching Algorithm Based on the Strategy Optimization of RANSAC Algorithm
CAO Zhong-yan,SHI Lin-lin,LU En-xue,CHEN Si-da,LI Quan-bin
(Jiangsu Key Laboratory of Advanced Laser Materials and Devices,School of Physics and Electronic Engineering,Jiangsu Normal University,Xuzhou 221116)
江苏高校优势学科建设工程资助项目(No.PAPD)、2013年江苏省高等教育教改研究课题(No.2013JSJG155)、
1007-1423(2015)23-0042-04
10.3969/j.issn.1007-1423.2015.23.010
曹中琰(1995-),男,江苏徐州人,本科,研究方向为人工智能
施琳琳(1993-),女,江苏海门人,本科,研究方向为智能信息处理
卢恩雪(1994-),女,浙江台州人,本科,研究方向为数字信号处理
陈思达(1994-),男,福建福州人,本科,主研究方向为计算机软件开发
李全彬(1977-),男,山东临沂人,教师,博士,研究方向为人工智能
2015-06-16
2015-08-06
基于改进点模式指纹匹配算法在匹配速度与匹配准确率上的不足,提出一种新的指纹匹配算法。稀疏矩阵具有计算速度快、储存容量小的优点,本文将稀疏矩阵应用到指纹匹配算法中,通过稀疏矩阵进行指纹图像初匹配,并进一步通过RANSAC算法进行总体二次匹配,在提高算法速度的基础上,维持匹配的准确率。实验证明,该算法匹配速度快、误识率低、准确性高,是一种有效实用的匹配算法。
指纹匹配;稀疏矩阵;RANSAC策略
江苏省现代教育技术研究2013重点课题(No.2013-R-24729)
Aiming at the deficiency of the matching speed and accuracy of the fingerprint matching algorithm based on point pattern,proposes a new fingerprint matching algorithm by discussing the existing algorithms.According to the sparse matrix computing speed and storage capacity of small features,the sparse matrix is applied to the fingerprint matching algorithm to handle initial fingerprint image matching in this paper.And through the RANSAC algorithm for the second time overall matching,to maintain a higher algorithm speed,at the same time,to ensure the accuracy of the matching.The experimental results show that the algorithm has good matching speed,low error rate,high accuracy,and has good performance in all aspects,and it is expected to be a practical and effective matching algorithm.
