Excel软件在回归分析教学中的应用
2015-09-25刘力平
刘力平
(常德市二中 湖南常德 415500)

回归分析是高中数学必修3、选修1-2以及选修2-3的学习内容,数学必修3之后,学生已经学习了两个变量之间的相关关系,包括画散点图、最小二乘法求回归直线方程等内容。在人教A版选修1-2、2-3《回归分析的基本思想及其初步应用》这一节中进一步介绍回归分析的基本思想及其初步应用。这部分内容包括:线性回归模型的数学表达式,随机误差项产生的原因,使学生能正确理解回归方程的预报结果,并能从残差分析角度讨论回归模型的拟合效果,从相关系数、相关指数角度探讨回归模型的拟合效果,以及建立回归模型的基本步骤,介绍两个变量非线性相关关系等。
一、回归分析的基本思想及其步骤
回归分析在经济学、统计学、遗传学及日常生活中应用得非常广泛。例如,某种农作物的产量和温度有密切的关系,但产量不仅与温度有关,还和日照时间、湿度等有关。又如,人的身高和体重是相关的,但影响人的身高还有其他的因素。像这样的两个变量之间的关系我们称为相关关系,显然相关关系是一种不确定的关系,那么这种关系怎样用函数关系去表示呢?表示出来后的拟合程度怎样?这就是回归分析的内容。其方法过程可分为以下几个步骤:
1.画出两个相关变量的散点图;
2.根据散点图的大致形状,选择回归模型,若是线性相关关系的,可利用最小二乘法
3.对求得的回归方程的可信度进行检验,求出解释变量对预报变量变化的贡献率R2,画出残差图,并进行残差分析。
二、Excel在回归分析教学中的应用
由于回归分析的应用性和实践性很强,因此计算量大,如果采用常规的分析和手工计算或者计算器计算,不仅教师难教,学生也感觉枯燥。针对这种情况,笔者在教学中有意加强了Excel软件的应用,提高学生利用计算机进行数据分析处理的操作技能,不仅教学过程轻松,学生也取得了不错的学习效果。
下面以教材选修2-3中例1为例,详细介绍在教学中用Excel做回归分析的方法与步骤。
例1.从某大学中随机选取8名女大学生。其身高和体重数据如下表所示:
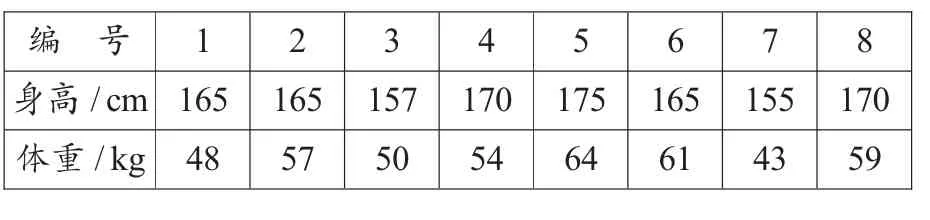
编 号 1 2 3 4 5 6 7 8身高/cm 165 165 157 170 175 165 155 170体重/kg 48 57 50 54 64 61 43 59
(一) 绘制散点图
1.打开Excel软件,在表格中输入身高和体重的数据(图1)

▲图1
2.选定身高与体重的全部数据,在插入菜单中打开图表(H)弹出如下对话框(图2),在图表类型中选择XY散点图,点击2次下一步。

▲图2
3.弹出图表选项对话框(图3),在标题选项中输入图表标题名称:散点图,在数值(x)轴、数值(y)轴中分别输入x轴和y轴,再单击下一步、完成,弹出散点图(图4)。
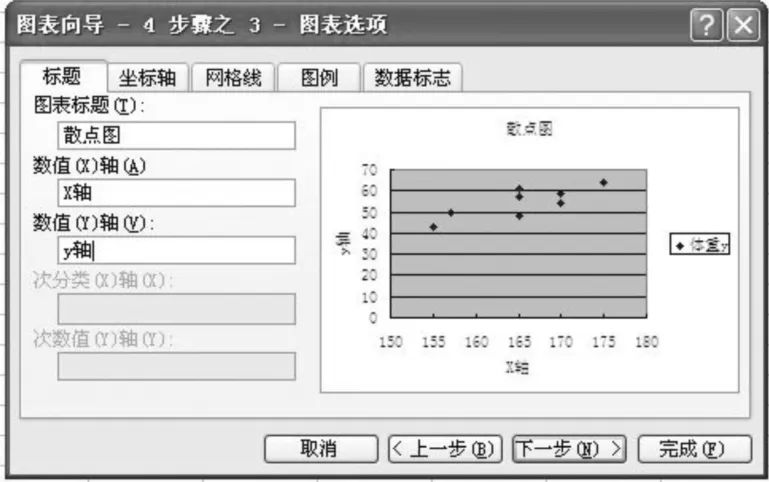
▲图3

▲图4
4.双击图表(图4) 的坐标区域,弹出图表区格式对话框(图5),可以对图表绘图区颜色、字体大小进行设置。双击击图表(图4)的x、y轴,弹出x、y轴格式对话框(图6),可以选取适当的刻度单位、最值等。如x轴格式对话框中最小值和最大值根据数据特点可以分别设为145和180,主要刻度单位可以选择5;y轴格式对话框中的最小值可以选择40,最大值选择70。
▲图5

▲图6
5.完成图表(图7):

▲图7
(二)回归直线方程的建立及拟合系数R2求法
观察散点图,让学生判断散点分布是否具有线性趋势。通过散点图可以判断,散点是呈条状分布的,说明身高和体重有比较好的线性相关关系,因此选择用回归直线y=bx+a来近似刻画它们之间的关系。
接下来,用Excel来求回归方程,步骤如下:
1.选中散点,点击鼠标右键,选择添加趋势线,弹出添加趋势线对话框,在选项卡中选择线性(图8),点击确定即可得到拟合直线(图 9)。

▲图8

▲图9
2.双击直线,弹出趋势线对话框,点击选项,选择显示公式和显示R平方值(图10),点击确定,即可得到回归直线的方程以及R2=0.6376, (图 11)。

▲图10

▲图11
这就是所求回归直线的方程,b=0.8485是回归方程斜率的估计值,说明身高每增加一个单位,体重y就会增加0.8485个单位,这说明体重和身高具有正的线性相关关系。R2=0.6376为拟合系数,表示解释变量与预报变量的相关关系,R2越接近1,表示回归的效果越好,R2越接近0,模型的拟合效果越差。图中表明“女大学生的身高解释了64%的体重变化”或者“女大学生的体重差异有64%是由身高引起的”。
(三)残差分析
1.将自变量X的数值由小到大的顺序进行排列,将图1中的数据重新进行排序,先选中编号、身高X、体重Y在内的所有数据。然后打开数据菜单,选择排序(S),弹出排序对话框(图12),在主要关键字中选择“身高X”,(其余不用选),选中升序排列。最后点击确定,得到身高从小到大排列好的数据(图13)。
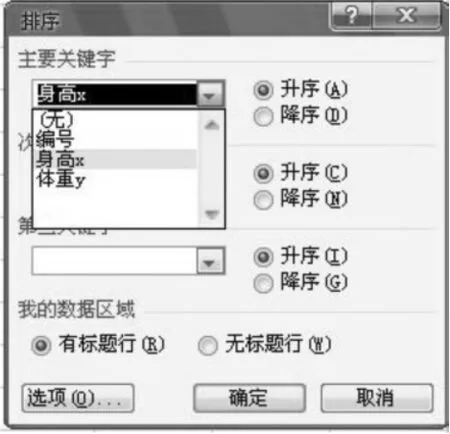
▲图12
▲图13
2.在工具菜单选项中选择数据分析选项,出现数据分析对话框(图14),在对话框中选择回归,点击确定,弹出回归对话框。

▲图14
3.在输入选项中,首先输入Y值区域:$D$2:$D$9和X值区域:$C$2:$C$9,也可以用鼠标在工作表中直接选中,然后选择置信度95%。在输出选项中,选择新工作表组,并命名。残差选项中选择残差和残差图。如图15所示:

▲图15
4.点击确定,在工作表中取得残差分析结果,如图16红色标注部分。此时得到的残差值和残差图是按自变量X的升序排列的。

▲图16
5.将得到的残差数据复制到工作表中,然后重新进行排序,再分别画出以编号、残差为变量散点图(图17)。

▲图17
三、小结
在回归分析教学中,Excel是很好的教学工具软件,利用这个工具软件,我们可以有效地解决回归分析教学中的难点问题,取得事半功倍的效果。同时,我们可以在教学过程中让学生自己动手操作,培养学生的动手能力,提高学生的信息技术素养,激发学生的学习兴趣。
[1]王黎明.应用回归分析[M].复旦大学出版社,2008.
[2]董凤鸣,周萍.excel在一元线性回归分析中的应用[J].科技信息,2007 (12):144-145.
[3]张海燕.解一元线性回归问题[J].天津农学院学报,2002(4) .
