数据库表与MATLAB矩阵间的转化推理及其应用

柴俊霞，薛瑞，刘道华

（1.北京市东城区职业大学计算机系，北京　100020；2.信阳师范学院计算机与信息技术学院，信阳　464000）

数据库表与MATLAB矩阵间的转化推理及其应用

柴俊霞1，薛瑞2，刘道华2

（1.北京市东城区职业大学计算机系，北京100020；2.信阳师范学院计算机与信息技术学院，信阳464000）

0　引言

在专家系统知识库的建造上，目前形式多样，有基于谓词的逻辑表示；有基于层次结构的树状表示；有基于面向对象的框架表示；有基于神经网络的节点表示［1］。随着近年来网络的发展，建造分布式协同专家系统的需求已迫在眉睫，然而在基于Internet网络的数据库中知识的访问就要考虑到知识库的存放形式，也就是要分析专家系统知识库存放的空间复杂度，以及其推理速度上的时间复杂度［2～4］。然而基于SQL Server及Access等大型综合数据库是网络数据存放的最好形式，因此这种数据库存放知识的形式也是建造分布式协同专家系统知识库的理想形式，同时其数据存放的规范性便于专家系统知识的获得，也有利于推理机对数据的访问［5］。一定知识库的存放形式也决定了一定形式的推理机制，以往的推理机制形式多样，但大都没考虑应用前景，而在许多工程专家系统的建造中，要用到许多工程计算及工程设计的优化，因此以往的专家系统推理机制很难与工程计算及优化相接合［6］。本文正是基于此种思想，利用MATLAB强大的矩阵处理能力图形可视化功能，建造了专家系统中知识库的数据表与MATLAB矩阵间的转化推理机制，并给出该种机制的推理实例，同时分析了其在专家系统建造中的应用。

1　专家系统中知识的数据库存放形式

专家系统中知识的表示存在确定性及不确定性两种，其推理的规则也有其规则的可信度，因此对于产生式规则由于其有规范的构成形式，如：

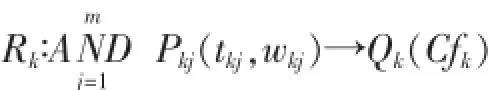
式中Pkj（Pk1，Pk2，…，Pkm）分别表示规则的前提断言（子前提）；tkj为第k条规则第j个断言的可信度值，表示该断言的确定性程度；wkj为规则的权重，满足关系；Qk表示第k条规则的结论；Cfk为第k条规则的可信度，其为一数值。为了保证数据表的一致规范性，在建立知识库时均用特定的标号来存放其对应的事实及其相关可信度因子，为了提高推理机搜索速度，在知识库表的存放时，把具有相同类的规则进行分组处理，将描述某一问题的关系规则存放在一张数据表中，因此其表的形式如下：规则编号（C，3）、事实编号1（C，3）、编号1可信度因子（N，3）、事实编号2（C，3）、编号2可信度因子（N，3）、…、结论事实编号1（C，3）、结论事实编号2（C，3）、…、规则的可信度因子（N，3）。

2　数据表与矩阵间的推理方法

将要推理的事实规则进行归一化处理，并将归一化处理后的结果映射到数据库一张表上，之后将已知推理事实映射到m×n的矩阵中，将矩阵的基本操作改变为矩阵结论部分映射的矩阵列的值，然后再将处理后的矩阵再映射返回到事实表中，且将推理出的结果部分值在事实表的编号中寻找，从而获得新的事实表，如果出现有多条结论，系统将采用冲突消解，之后由得到的事实表再一次映射到矩阵中，如此循环，一直到最终获得结论为止。

为了简化规则中出现的可信度计算及多结论事实的出现（其实存在也一样），假设存在有如下规则库（表1）。

则有上规则库对应的规则库表如表2所示。

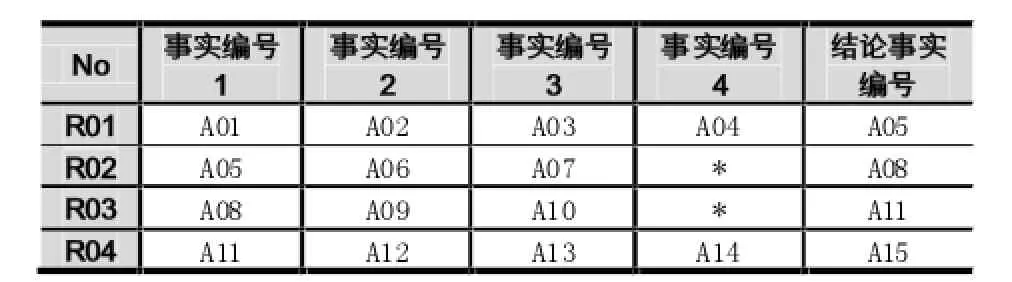
表2　规则库表

现假设存在如下已知推理事实：

机构运动形式为精确（A01），机构结构形式为紧凑（A02），机构传动效率高（A03），机构响应速度快（A04），传动比确定（A06），载荷计算满足（A07），为重载荷 （A09），为重要应用 （A10），齿轮材料为40（r）（A12），为中等冲击（A13）

则由上已知推理事实映射对应的数据库表如表3所示。

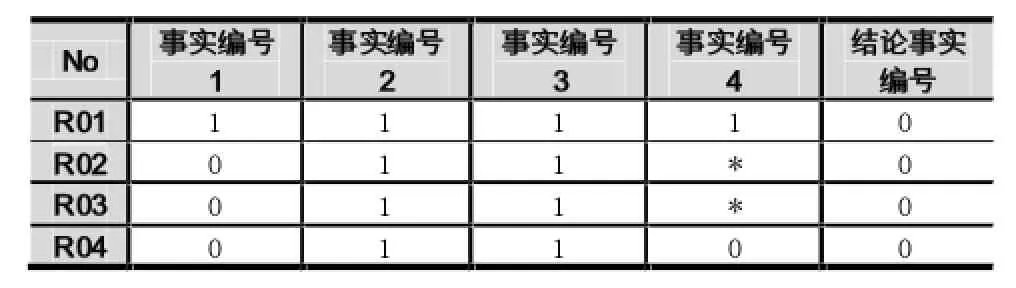
表3　数据库表

当矩阵多行同时存在“1”时，则采用冲突消解进行处理。

由上处理后的矩阵转化为事实表如表4所示。

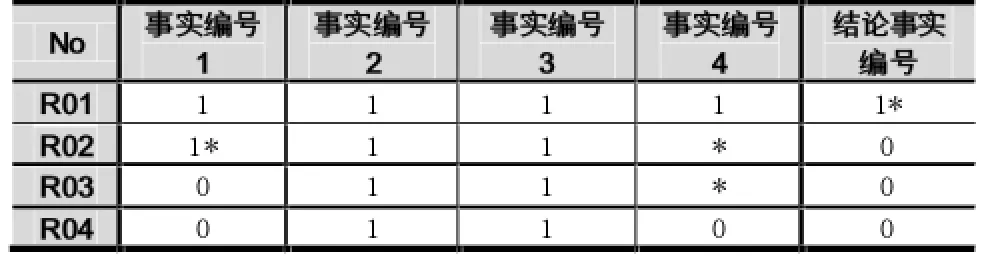
表4　矩阵运算后的转化的事实表

由表4的事实表再转化为矩阵，其结果如下：

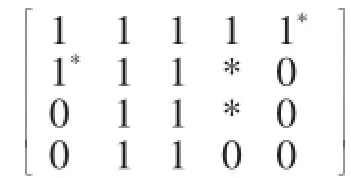
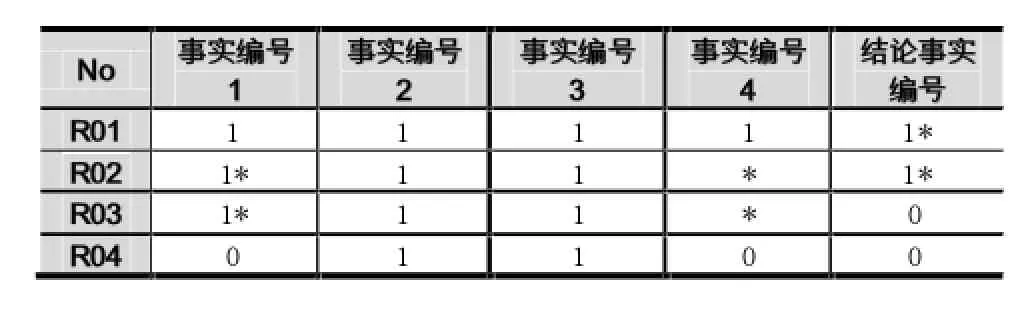
表5　矩阵运算后的转化的事实表

由表5的事实表再转化为矩阵，其结果如下：

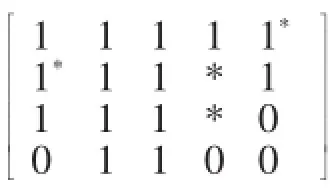
由上处理后的矩阵转化为事实表如表6所示。

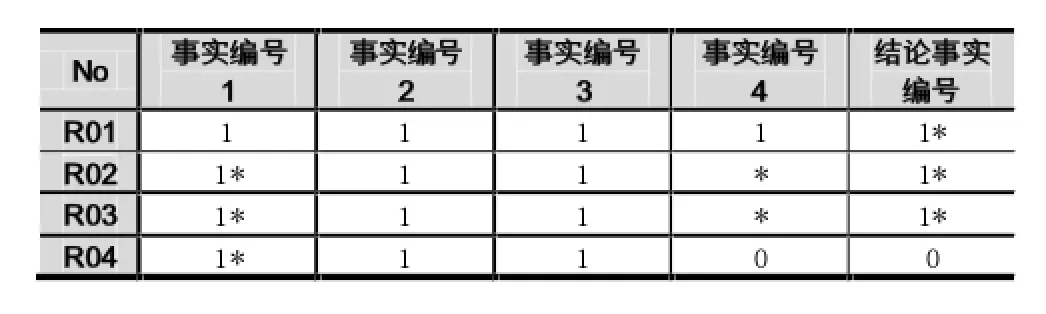
表6　矩阵运算后的转化的事实表

由表6的事实表再转化为矩阵，其结果如下：

（1）当A14存在时，推出结论为A15，即：用整体淬火热处理方式；

（2）当A14不存在时，推出结论为A11，即，选硬齿面形式。

3　专家系统应用中的推广

基于符号处理的专家系统具有易解释的机制但其存在推理速度慢的局限性，而具有形象思维的连接机制具有并行快速推理但难以解释的局限性，因此人们想方设法获得两者的优点，而建立混合智能专家系统又是目前研究的热点，然而两者很难在知识表达上相互转化，基于本文提出的数据库表与MATLAB矩阵的转化推理中出现了对应的“0-1”结构，因此利用规则的数据表转化为对应的MATLAB矩阵中的每一行正好对应为规则库中的一条规则，这样就很容易把此条规则作为ART1（Adaptive Resonance Theory）神经网络的输入，对于出现的非“0-1”结论，仍可采用数据归一化处理后转化为［0，1］区间内的任一实数值，此时可采用神经网络ART2结构形式作为神经网络的输入，这样规则库中的每一条规则经MATLAB转化后的矩阵行均可作为神经网络的训练样本，通过网络的训练来固化网络的权值，也就是将知识的表示转化为网络的权值及阈值表达上，进而采用基于模糊的神经网络推理机制来实现快速的并行处理，同时在转化中对改变值的地方采用二维数组记录推理中的规则变化，便于作混合智能专家系统的解释使用。

4　结论

本文分析了专家系统中知识库的存放形式；给出了数据库表与MATLAB矩阵间的相互转化的推理原理，分析了这种表-阵转化中出现的“0-1”结构在神经网络及遗传演化算法中的应用，该机制是建立分布式协同混合智能系统的很好结合点。

［1］尹朝庆，尹皓.人工智能与专家系统［M］.北京：中国水利水电出版社，2002

［2］栗然，卢锦玲.基于关系数据库的电网结构知识表示［J］.电力系统自动化，2002，21（5）：71～72

［3］袁璐，刘峰，廖洁.基于知识的土地利用数据综合［J］.2010，30（12）：3385～3387

［4］Raed I H，Syed I A，Rafat P.Designing Genetic Regulatory Networks using Fuzzy Petri Nets Approach［J］.International Journal of Automation and Computing，2014，7（3）：403～412

［5］Iluju K，Alfredo G.Synthesizing Advanced Transaction Models using the Situation Calculus［J］.Journal of Intelligent Information Systems，2014，35（2）：157～212

［6］王生生，刘大有，谷方明，等.基于ALC的空间语义知识库［J］.吉林大学学报，2011，41（2）：424～429

Database Form；MATLAB Matrix；Form-Matrix Reasoning of Transforming；0-1

Transformation Reasoning Between Database Form and MATLAB Matrix and
Its Application

CHAI Jun-xia1，XUE Rui2，LIU Dao-hua2
（1.School of Computer，Beijing Dongcheng District Vocational University，Beijing 100020 2.School of Computer and Information Technology，Xinyang Normal University，Xinyang 464000）

河南省基础与前沿计划研究项目（No.142300410393）、河南省教育厅科学技术研究资助项目（No.14A520001）

1007-1423（2015）09-0043-04

10.3969/j.issn.1007-1423.2015.09.010

柴俊霞（1978-），女，山西运城人，硕士，讲师，研究方向为神经网络及其应用

薛瑞（1979-），女，河南信阳人，硕士，讲师，研究方向为智能算法

刘道华（1974-），男，河南信阳人，博士，教授，研究方向为智能算法

2015-01-13

2015-02-13

分析基于产生式规则的数据库存放形式，提出专家系统中规则的数据库表与MATLAB矩阵间的转化推理方法，给出这种表-阵转化的推理实例，进而由表-阵转化推理的“0-1”结构分析其在神经网络及遗传演化算法中的应用。

数据库表；MATLAB矩阵；表-阵转化推理；“0-1”结构的应用

Analyzes database form that is based on producing type regular data stock，proposes the transformation reasoning method among the regular database form and MATLAB matrix in the expert system，provides this kind of form-matrix reasoning instances，and then by the form，matrix transform"0-1"of reasoning structure，analyzes their evolve the application of algorithms in neural network and heredity.