基于压缩感知的自旋目标平动速度及周期估计算法

陈雁泳，邓振淼（厦门大学通信工程系，厦门　361000）

基于压缩感知的自旋目标平动速度及周期估计算法

陈雁泳，邓振淼
（厦门大学通信工程系，厦门361000）

0　引言

近年来，目标微动特征提取在雷达目标探测与识别中受到广泛关注［1～4］。微动是指雷达目标除质心平动以外的小幅振动、转动和其他高阶运动，由微动产生的多普勒频率为微多普勒频率，不同的微运动会产生不同的微多普勒。对于空间目标成像雷达而言，有些目标在高速飞行过程中常带有自旋运动。如飞机螺旋桨、导弹弹头，和空间碎片等都具有自旋的特性。此种自旋特性表现在时频谱上即为目标的微多普勒。此时对目标的微多普勒的参数估计，如自旋周期和平动速度等，在目标识别、弹道导弹防御系统等领域有重要的应用价值。文献［5］分析了基于微多普勒特征估计的弹道导弹识别的方法，文中采用了短时傅里叶变换分析了导弹的微多普勒频率，并基于实际弹头数据提出了时频变换最优的滑动窗窗宽长度。在雷达ISAR（SAR）成像中，目标微多普勒的存在会降低图像的可读性，为了提高成像质量，需要将微多普勒从目标回波中分离出来。文献［6］和文献［7］中介绍了如何消除微多普勒对ISAR （SAR）成像中的影响，提高雷达ISAR（SAR）成像质量。另外，由于远程探测雷达在探测时为获得可靠的目标距离测量值而普遍采用低重复频率工作方式，从而对目标微动引起的微多普勒会产生严重的模糊。文献［8］分析了微多普勒模糊产生的具体原因，但没有提出解决方法。文献［9］和文献［10］提出了基于压缩感知理论的多普勒解模糊，但是对于目标的微动不适用。如果雷达发射高重复频率的脉冲用于提取目标微动特性，则一方面会浪费雷达的时间资源，雷达的时间资源对需要同时跟踪多目标的相控阵雷达来说是非常宝贵的；另一方面，因高重复频率的脉冲串信号脉冲宽度受限，相应的回波信号较弱，导致作用距离受限。本文研究在不提高雷达的工作频率情况下如何从雷达回波中提取自旋目标的周期及平动速度，从而能够更好地为后续提取目标无模糊的微多普勒时频谱打下基础。

在以上工作的基础上，本文提出了一种新的基于随机稀疏采样的加窗压缩感知的自旋目标周期提取方法。首先，对传统固定重复频率的脉冲发射时刻加上随机扰动构成脉冲发射时刻序列，为了进一步减少脉冲发射序列，再从具有随机扰动的脉冲发射时刻中随机抽取部分脉冲，构成稀疏的具有随机扰动的脉冲发射时刻序列，雷达按这些时刻发射信号，回波经过匹配滤波之后可以看成是稀疏采样的包含目标特性的回波。接着利用发射时刻序列构造相应的感知矩阵，利用构造的感知矩阵和压缩感知重构算法恢复出滑动窗内信号的频率值，提取目标微多普勒时频谱，然后再利用压缩感知算法估计出自旋周期，进而可以利用估计的自旋周期估计出目标的平动速度。

1　信号模型

首先给出目标模型，如图1所示，假设经过运动补偿后目标的残余速度为v，由于在相关时间内雷达和目标相对转角很小，假设可以忽略。目标以角速度ωs绕轴自旋运动，则目标上一点（Ricosθi，Risinθi）到雷达的瞬时距离为：

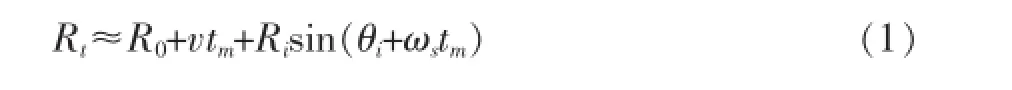
其中R0为起始时刻目标与雷达的距离，v为径向速度，ωs为目标自旋角速度。

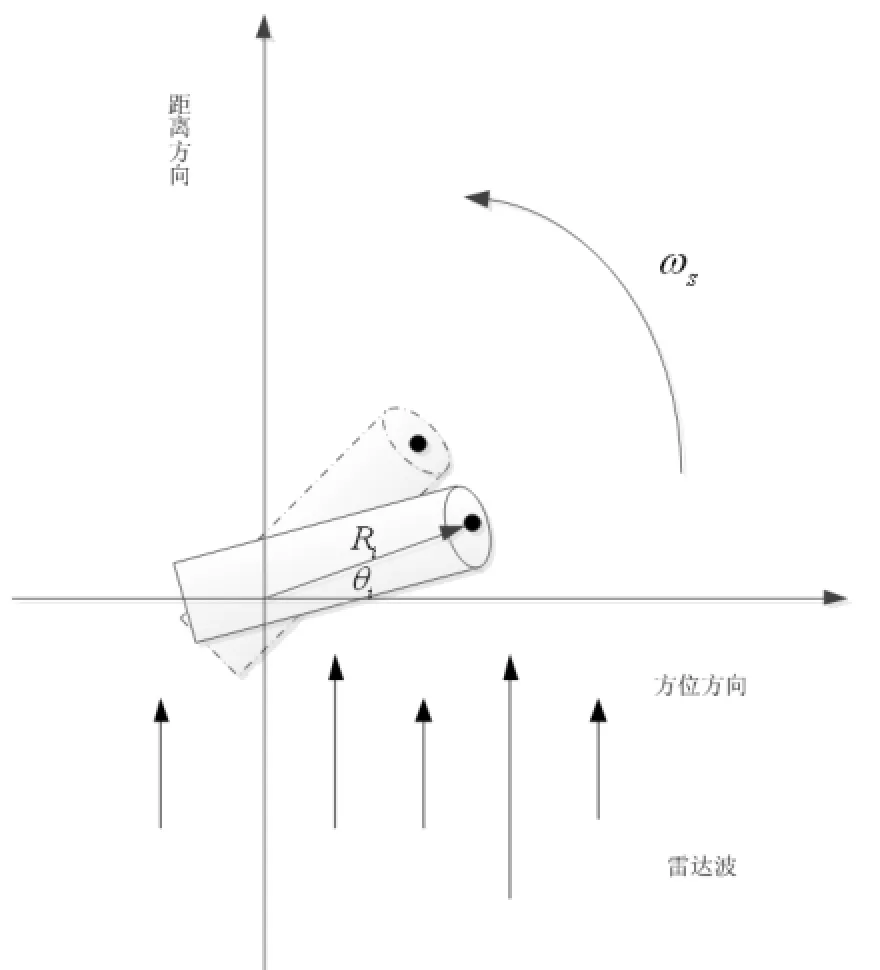
图1　

假设雷达发射的LFM信号为：

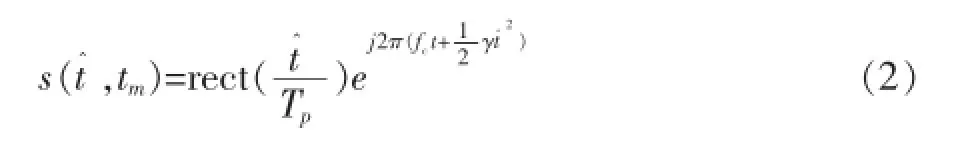
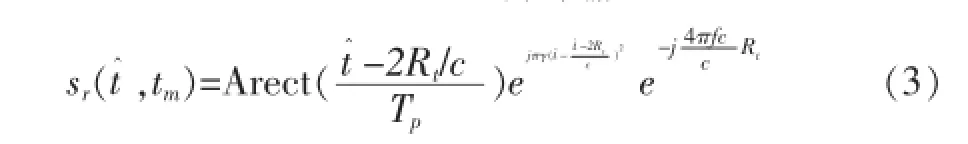
其中：A是散射点回波的幅度，c是光速，Rt为雷达与目标之间的瞬时距离。回波信号经过匹配滤波并变换到距离频域之后，其信号表现形式r（fr，tm）为：

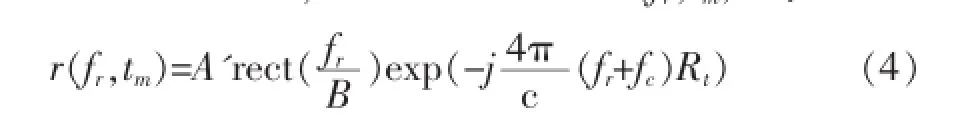
其中：B是信号带宽。

式（1）代入式（4）可以得到慢时间域雷达回波

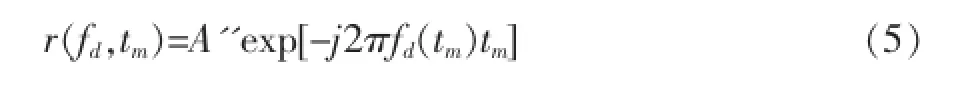
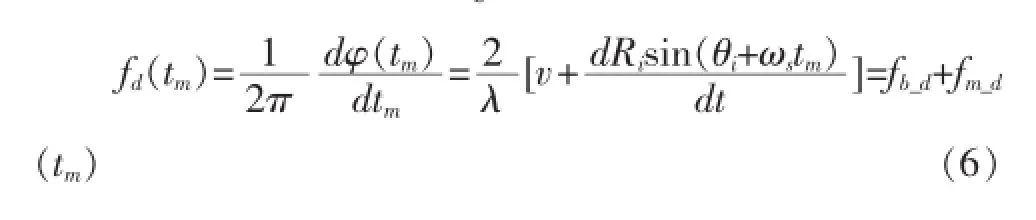
由式（6）可见，fb_d将时频谱沿频率轴整体移动而不改变谱的形状，fm_d（tm）决定谱的形状，这两项对时频谱的作用分别如图2和图3所示。

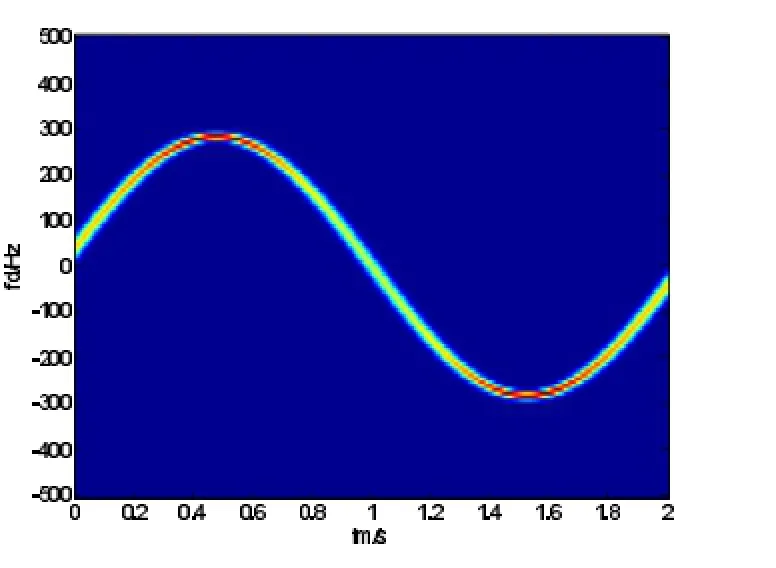
图2　

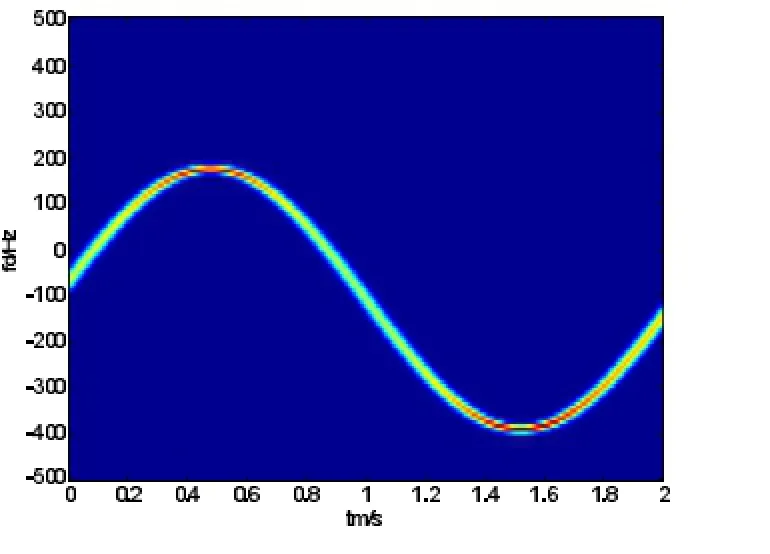
图3　

若目标上有多个散射中心，则目标回波表现为多个散射中心的回波的线性叠加：

体现在时频谱如图4和图5所示：

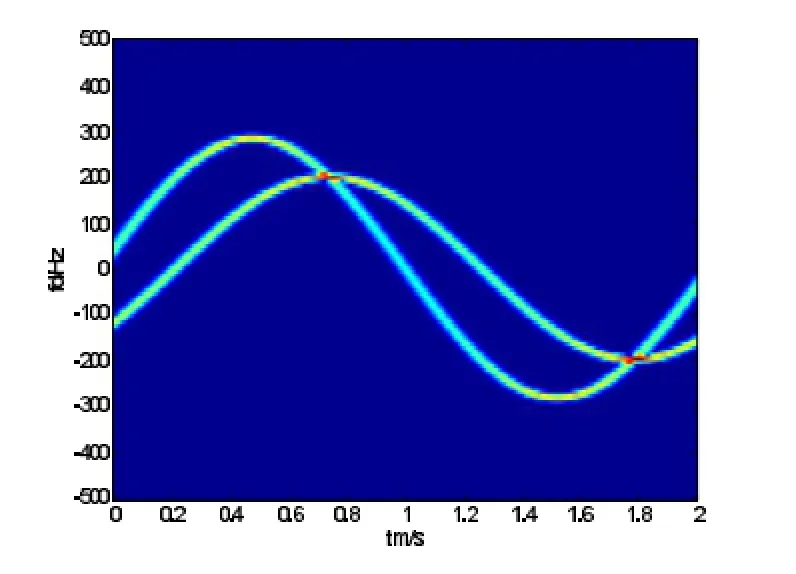
图4　

图5　

2　利用压缩感知提取目标自旋周期

分析式（6）和图3可以看出，自旋运动的微多普勒时频谱为正弦波形，且目标的自旋频率即为正弦波的频率，由此可以想到利用压缩感知来提取正弦曲线的频率。本文提出一种基于压缩感知的周期提取方法。首先利用加窗压缩感知的方法来提取目标的时频谱 （区别于以往的短时傅里叶变换），然后利用压缩感知对时频谱进行估计，提取出正弦波的频率，即为目标的自旋周期。

2.1压缩感知

压缩感知理论指出：如果信号x（x∈RN）经过正交变换基Ψ投影后是稀疏或可压缩的，则可设计一个与Ψ不相关的测量矩阵φ线性测量信号，得到只包含信号主要信息的M（M＜N）个测量值y（y∈RM）

通过对这M个测量值求解优化问题，可以实现原信号的近似重构。由于x是可稀疏的

式中Θ=φψ为M×N的矩阵，称为感知矩阵。只要矩阵Θ服从“有限等距性质（Restricted Isometry Property，RIP）”，稀疏信号就能够从M个测量值y重构。

从式（6）可以看出，在某段时间（fk_d（tm）可看作为常数）内，r（fd，tm）在傅里叶变换域上可稀疏，因此稀疏矩阵ψ可取为傅里叶变换基，即：

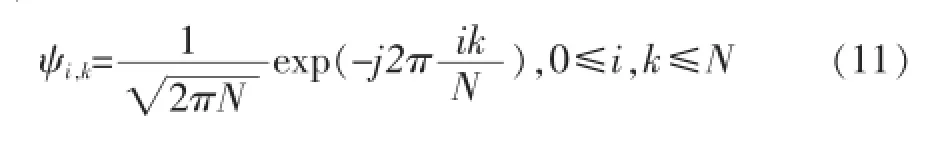
信号重构是从测量值y中重建原始信号~x。最简单的方法是解l0范数最小化问题，如：

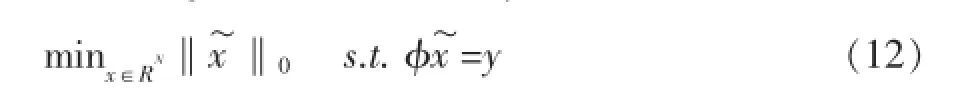
l0最小化问题在理论上是最优的，但在数值上是不可行的，属于NP难题，需要列出x非零值的种可能组合，求解的数值不稳定。Donoho等人提出用l1范数代替l0范数会得到相同的解［13］。

解l1范数是一个凸优化问题，可以转化成线性规划问题求解。

为了得到精确的重构信号，通常M的取值与φN×N和稀疏矩阵Φ的相关度u（ΦN×N，ψ）需满足一定的关系式：

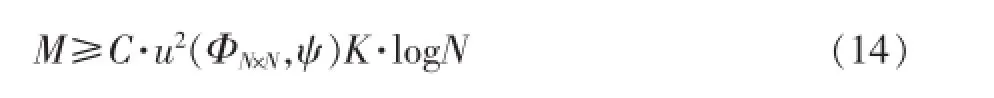
C为确定常数，相关度u（ΦN×N，ψ）越小，信号完全重构需要的M值越小。相关度u（ΦN×N，ψ）的定义为［14］：

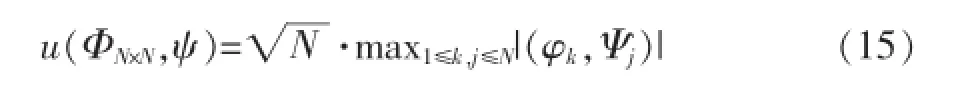
典型的恢复算法有基追踪法和贪婪匹配追踪法。基追踪算法具有全局最优的优点，但计算复杂度高；贪婪匹配追踪算法，如正交匹配追踪、迭代阈值法和正则化正交匹配追踪算法等，是一种局部最优化方法，比BP算法的处理速度快［14］。

2.2加窗压缩感知

远程雷达的脉冲重复频率fs较低，当雷达工作于固定重复频率时，慢时间域雷达回波存在严重的多普勒模糊。如果在脉冲发射时刻上叠加随机扰动Δi，得到新的脉冲发射时刻序列t'i=ti+Δi等效于从一个高重复频率的脉冲发射时刻序列中随机抽取得到。

而且由于微多普勒的特殊形式，无法找到合适的感知矩阵可以直接利用重构算法恢复微多普勒时频谱。但由式（6）可以看出，在一个短时间twindow内，fd（tm）可近似为一个常数，故可采用以下办法：对接收到的回波信号加滑动窗（滑动窗的大小使得fd（tm）近似为常数），则窗内信号变为：

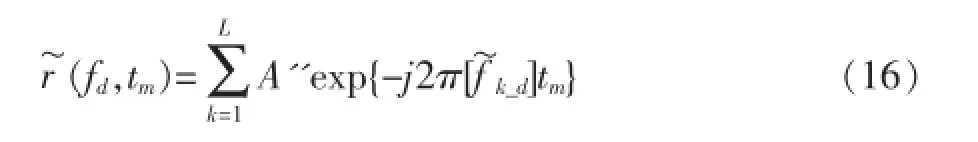
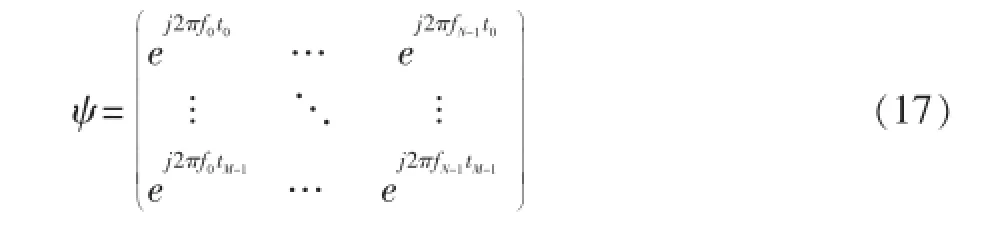
其中tn，n=0，1，…，M-1为滑动窗所对应的时间序列，fn，n=0，1，…，N-1为细化的多普勒频率。滑动窗每滑动一个时刻，利用滑动窗的时间序列构造相应的感知矩阵，然后利用重构算法恢复出窗内信号（fd，tm）的多普勒频率k_d。最后，将得到的多普勒频率沿着时间轴排列，即得到微多普勒时频谱。若要提高估计窗内信号的无模糊多普勒频率的精度，可以采用文献［15］提出的感知矩阵自适应细化方法，从而得到更高分辨率的多普勒频率。

只要感知矩阵满足RIP特性并且测量值个数满足式（14），利用重构算法就可以从（fd，tm）中恢复出滑动窗内信号的多普勒频谱，因此ti'可以进一步稀疏。首先从传统雷达固定重复频率发射时刻t1，t2，…，tn中随机选择M个时刻，然后给每个选择出的发射时刻加上随机扰动Δk，其中Δk～N（0，ξ2）。这样，雷达脉冲发送时刻可以表示为：

其中k代表时间的索引值，是｛1，2，…，n｝的一个子集，即k=｛k1，k2，…，kn｝｛1，2，…，n｝。

在实际应用中，基于以下两个因素扰动项Δk不能完全随机：（1）雷达必须按照雷控的时钟节拍工作，因此Δk的精度不能高于雷控的时钟精度；（2）理论上Δk的精度越高，通过细化基矩阵，多普勒无模糊范围越大。然而，由于基矩阵采用的是DFT基，而文献［15］指出，DFT基的细化倍数与稀疏测量样本个数之间满足该文中式（20）的关系，即随着DFT基细化倍数的增加，样本个数也要相应增大，二者之间存在折衷的关系。除此以外，细化倍数越大，重构算法的性能受测量噪声的影响越大。

利用加窗压缩感知的方法提取出目标微多普勒时频谱后，因为自旋目标的微多普勒时频谱为正弦曲线，故此时再次利用压缩感知估计自旋目标时频谱的频率，最后得到目标的周期。具体算法流程图如图6所示：

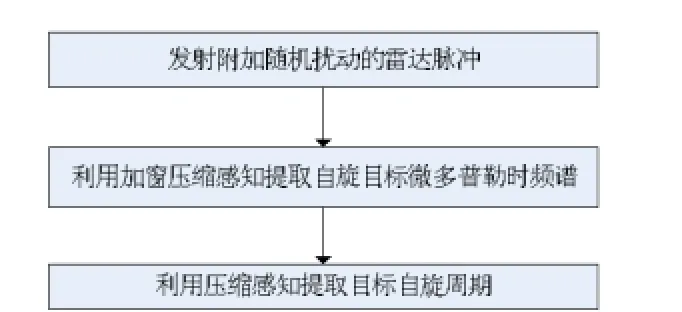
图6　

3　利用提取出的微多普勒曲线估计残余速度的算法

由式（6）可知，自旋目标微多普勒时频谱为：

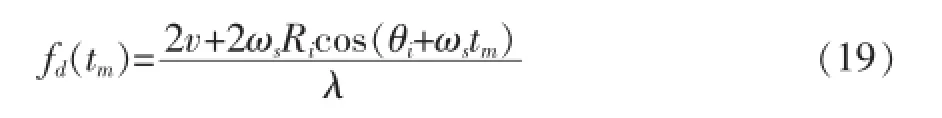
对（19）进行积分，积分区间为整数倍周期可得：

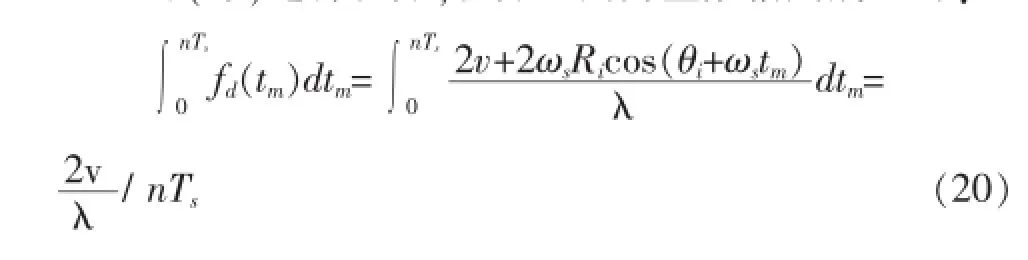
故可以通过（20）计算出实际物体的残余运动速度。

4　仿真实验

对本节算法进行仿真，仿真条件如表1所示：

表1

利用2.1中加窗压缩感知的方法提取出目标自旋的微多普勒时频谱如图7所示：

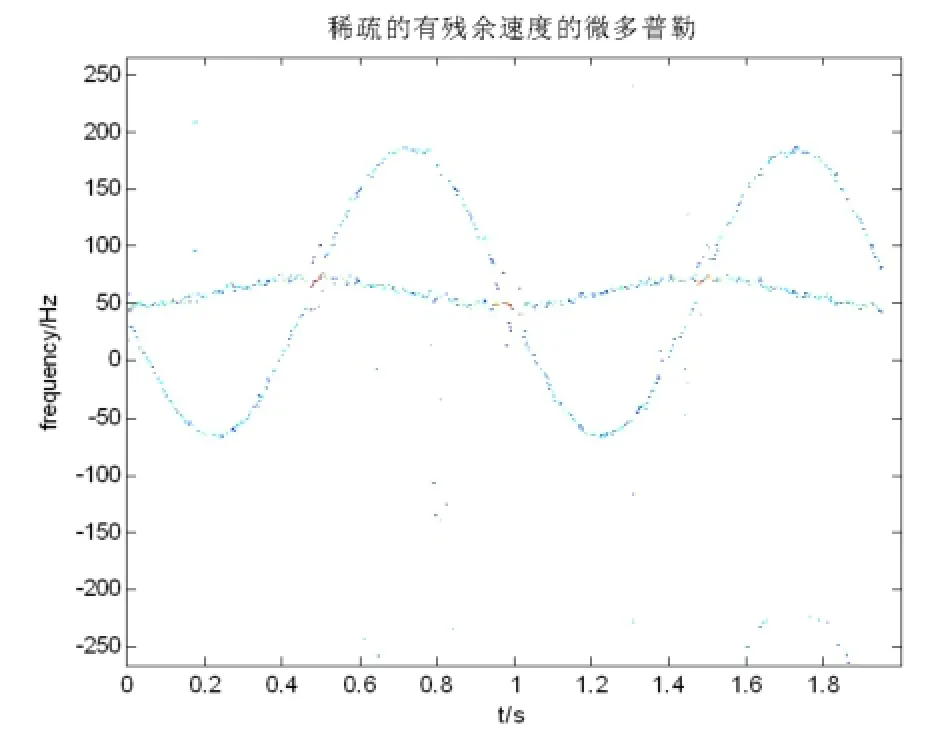
图7　

由图 7可知为正弦曲线，由于已经具有随机特性，故可直接2.1所述的压缩感知来估计正弦曲线的频率，估计出的频率如图8所示。

如图8所示：可得正弦曲线的频率为1Hz，故微动的周期Ts=1s。由 （20）进而估算出目标残余速度v= 0.89m/s。与上述仿真参数一致，验证了算法的有效性。

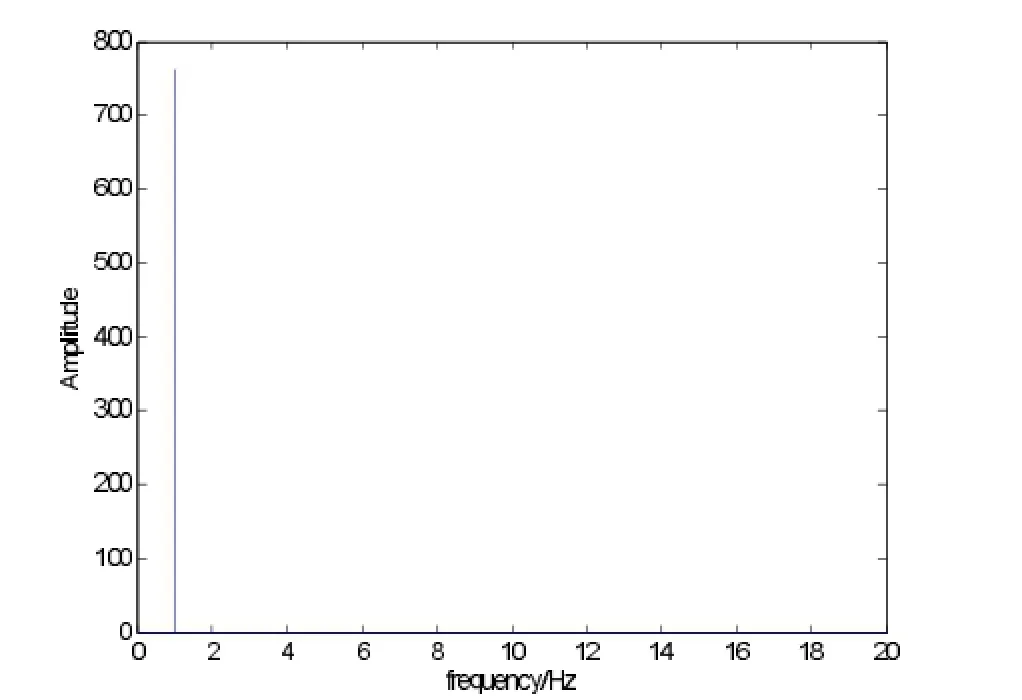
图8

5　结语

基于雷达回波信号的频域稀疏特性和压缩感知理论的结合，本文提出了一种基于压缩感知的提取微多普勒周期的新方法。通过合理地设计雷达脉冲发射时刻，可以得到慢时间域稀疏雷达回波测量值，然后利用重构算法和加滑动窗的方式首先提取出目标自旋的微动时频谱，然后再次利用压缩感知提取出目标的自旋周期，对提取的时频谱进行积分，最后估计出目标的残余速度，具有很高的应用价值。

［1］T.THayaparan L.J.Stankovic，M.Dakovic，V.Popovic，Micro-Doppler Parameter Estimation from a Fraction of the Period.IET Signal Processing，10.1049/iet-spr.2009.0093

［2］K.Li，Y.Liu，K.Huo，W.Jiang，X.Li，Z.Zhuang，Estimation of Micro-motion Parameters Based on Cyclostationary Analysis，IET Signal Processing.10.1049/iet-spr.2009.0044

［3］T.Thayaparan，P.Suresh，S.Qian，K.Venkataramaniah，S.SivaSankaraSai，K.S.Sridharan，Micro-Doppler Analysis of a Ratating Target in Synthetic Aperture Radar，IET Signal Processing 10.1049/iet-spr.2009.0094

［4］T.Thayaparan，L.Stankovic，I.D，Jurovic，Micro-Doppler-Based Target Detection and Feature Extraction in Indoor and Outdoor Environments.Journal of the Franklin Institute 345（2008）700～722

［5］Lihua Liu，DesMcLernon，Mounir Ghogho，Weidong Hu，Jian Huang，Ballistic Missile Dection Via Micro-Doppler Frequency Estimation from Radar Return.Digital Signal Processing 22（2012）87～95

［6］S.B.Colegrove，S.J.Davey，B.cheung，Separation of Target Rigid Body and Micro-Doppler Effects in ISAR Imaging，IEEE Transactions on Aerospace and Electronic Systems Vol.42，No.4 October 2006

［7］Ljubisa，Stankovic，Thayananthan，Thayaparan，Milos，Dakovic，Vesna.Popovic-Bugarin，Micro-Doppler Removal in the Radar Imaging Analysis，IEEE Transactions on Aerospace and Electronic Systems Vol.49，No.2 April 2013

［8］高红卫，谢良贵，文树梁，匡勇.弹道导弹目标微动特性的微多普勒分析与仿真研究.系统仿真学报，2009

［9］Y.H.Quan，L.Zhang，M.D.Xing，Z.Bao.Velocity Ambiguity Resolving for Moving Target Indication by Compressed Sensing.ElectronicsLetters 27th October 2011 Vol.47 No.22

［10］Zhang Yu-xi，Sun Jin-ping，Zhang Bing-chen，et.al.Doppler Ambiguity Resolution Based On Compressive Sensing Theory［J］.Journal of Electronics&Information Technology，2011，33（9）：2103～2107

［11］Mallat S.Zhang Z.Matching Pursuit with Time-Frequency Dictionaries［J］.IEEE Trans.on Signal Processing，1993，41（12）：3397～3415

［12］Chen S，Donoho L，Saunders M.Atomic Decomposition by Basis Pursuit［J］.Siam Review，2001，43（1）：129～159

［13］David L.Donoho，Michael Elad.Optimally Sparse Representation in General（Nonorthogonal）Dictionaries Via Minimization［J］. PNAS，March，2003，100（5）：2197～2202

［14］Wang Jun-hua，Huang Zhi-tao，Zhou Yi-yu，et al..Generalized Inchoherence Principle in Compressed Sensing［J］.Signal Processing，2012，28（5）：675～679

［15］Hu Lei，Shi Zhi-Guang，Zhou Jian-Xiong，et.al.Compressed Sensing of Complex Sinusoids：An Approach Based on Dictionary Refinement［J］.IEEE Trans.on Signal Processing，2012，60（7）：3809～3822

Micro-Doppler Time-Frequency Spectrum；Compressed Sensing；Random Perturbation；Sliding Window Compressive Sensing

Translational Velocity and Cycle Estimation of Spin Target Based on Compressed Sensing

CHEN Yan-yong，DENG Zhen-miao
（Department of Communication Engineering，Xiamen University，Xiamen 361000）

1007-1423（2015）09-0003-06

10.3969/j.issn.1007-1423.2015.09.001

陈雁泳（1989-），男，江苏无锡人，硕士研究生，研究方向为雷达信号处理

2015-02-26

2015-03-16

给出一种新的利用压缩感知来估计自旋目标周期及平动速度的算法。该算法的基本原理是雷达在随机的时刻序列发射脉冲信号，采集匹配滤波后的信号值，通过对信号值加滑动窗，利用加窗压缩感知的方法提取出目标的微多普勒时频谱，再次利用压缩感知算法提取出目标的旋转周期，进而提取出目标的残余平动速度，具有很高的应用价值。

微多普勒时频谱；压缩感知；随机扰动；加窗压缩感知

邓振淼（1977-），男，福建龙岩人，博士，副教授，研究方向为雷达信号处理

Proposes a novel method based on CS theory to estimate the translational velocity and cycle of spin target.Transmits a pulse train with the random and sparse transmitting time and obtains the received signals after matched filtering.The signal is multiplied by a sliding window and the unambiguous micro-Doppler time-frequency spectrum can be obtained based on the sliding window compressive sensing.By the compressed sensing，estimates the circle and translational velocity of spin target.This method has very high practical value.