协作通信网络基于能量效率的博弈模型*

谈 程，吉庆兵

0 引言

协作通信由于充分利用空间分集和多用户分集带来系统性能提升受到越来越多关注，作为4G通信关键技术，更成为了通信领域的研究热点。协作通信思想可以追溯到Cover等人对中继信道信息论特性的研究［1］。协作通信综合了分集技术和中继技术，在不增加天线情况下，实现了虚拟多天线传输。虽然如此，但网络中用户能量有限一定程度上限制了网络性能的提升，因此能量效率是衡量协作通信系统性能好坏的一个关键指标。

在多用户OFDM协作通信网络中，资源分配问题主要包括中继选择［2］和子载波和功率的分配［3］。用户将部分子载波用于转发他人数据，其余用于发送自身数据。被帮助用户的功耗因此减少，而提供帮助的用户的功耗会增加，但通过资源的合理分配，能够达到节省总功耗的效果。

联盟博弈［4］作为有效理论工具可用来研究网络资源分配问题。用户间数据交换形成网络拓扑，只要通过直接链路或多跳路径，用户间就能建立通信关系组建联盟，而形成联盟能使资源共享。在一个稳定联盟中，没有用户希望脱离当前联盟，因为达到了一种“均衡”状态。目前大部分文献都未说明如何达到“均衡”状态，例如文献［5］阐述了只要总联盟中用户支付属于核心解，那么一定能形成总联盟，但没说明形成过程。本文就OFDM－TDMA接入方式分别研究非协作与协作这两种传输情形，最后通过建立动态联盟博弈模型来具体分析协作传输下的能量效率。

1 模型建立

假设整个OFDM通信系统在一个准静态衰落环境中运行，并且数据收发端都掌握CSI。用户各子载波上的信号在接收端的噪声均为加性高斯白噪声，满足 CN(0，N0)分布。K={1 ，2，…，K}表示用户节点集合，N={1 ，2，…，N}表示每个用户可用子载波，每个子载波所占带宽为W。每个数据传输周期分成K时隙，用户分别各占用一个时隙。在某一时隙，有N个子载波供对应用户传输数据。设P是一个K行N列的功率分配矩阵，行表示用户，列表示子载波。对于k∈K，n∈N，P中第k行第n列元素Pkn表示用户k分配在子载波n上的功率。p为K维向量，其第k个分量pk表示用户k分配在N个子载波上的总功率，即

设用户功率上限向量为pmax=(pmax1，…，pmaxK)，则有p≤pmax。用户k的数据传输率记作Rk，

Rkn为k在子载波n上的数据子流的传输率。

假设采用MPSK调制机制，如果接收信号的信噪比为γ，那么数据误码率为［6］

其中b=sin2(π/M)。假设φ0是可接受最大误码率，则 φ(γ)≤φ0。但(3)中被积项不可积，φ(γ)≤φ0很难进一步化简。而φ(γ)关于γ递减，如果找到 γ0使得 φ(γ0)=φ0，只需满足 γ≥γ0，通过龙贝格求积公式可近似得到γ0。

2 非协作传输

在非协作情形下，用户将自己发送的高速数据流分成N个并行低速数据子流，各子流被调制到不同子载波上。gkn表示用户k与基站之间的基于子载波n的信道增益，对应信噪比为

那么k基于子载波n的传输率(bit/s)为

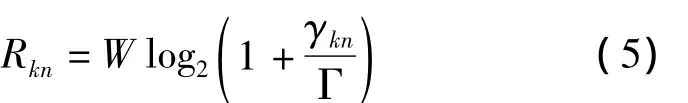
Γ表示理论与实际信道容量间的差异。用ηk评估k的能量效率，即消耗单位功率给k带来的传输率，

Rk和 pk分别乘以传输时间 ΔT，RkΔT 表示 ΔT 内k传输的数据比特，pkΔT表示ΔT内k消耗的能量，实际上ηk表示的是k消耗单位能量传输的数据比特。令 η =(η1，η2，．．．，ηK)，在误码率性能限制下，为最大化各用户的能量效率，有

在非协作情形下，各用户的传输是相互独立的，因此上述优化问题可分割成K个独立的子问题，具体求解我们后面会介绍SQP［7］算法。

3 协作传输

在协作通信系统中，当用户发送数据至基站时，由于无线通信网络的广播特性，其他用户也可以接收到该用户发送的信号，某些用户可充当该用户的中继。根据子载波的用途，可以分成三类:

1)发送自己的数据，数据没有被转发;

2)发送自己的数据，数据被转发;

3)转发其他用户的数据。

前两类子载波与用户传输率有关，3)类与其他用户传输率有关。对1)类子载波带来的传输率可通过(4)和(5)计算得到，而第二类子载波带来的传输率不仅与直接信噪比有关，也受到中继信噪比的影响。

设 glmkn(k，l∈K，n，m∈N)为用户 k 基于子载波n与用户l基于子载波m间的信道增益。为了符号统一化，将(4)中的gkn表示成gknkn。此外，对于任意k∈K，gkmkn=0(n≠m)。I是一KN阶方阵，表示子载波分配情况，Ilmkn为I的第［N(k－1)+n］行第［N(l－1)+m］列元素，要么等于1，要么等于0，具体意义如表1所示。

表1 I中元素的意义Table 1 Denotation of each element in I

那么用户k基于子载波n信号的信噪比为

上式右边第一项为k的直接传输信噪比，第二项为中继传输信噪比。在协作传输情形下，k的传输率可通过上式以及(2)和(5)得到。

4 联盟博弈理论引入

在联盟博弈中，称部分拥有共同利益的成员形成的集团为联盟，单个成员组成的集团称为单联盟，由所有成员形成的集团称为总联盟。在各联盟内部，成员间进行合作，通过合作获得的总收益在内部成员之间按某种规则进行分配。

4． 1 协作通信网络中联盟和联盟结构

用箭头表示协作关系，箭头从被帮助用户指向提供中继服务的用户。(m，n)表示被帮助的用户在子载波m上的数据被提供服务的用户通过子载波n转发。如图1所示，共有7个用户，每个用户有3个子载波可用。用户2通过子载波1帮助用户3，用户4通过子载波1帮助用户2，用户6通过子载波1和2帮助用户5。用户1和2互相帮助对方转发数据，而用户7不帮助其他用户也没有其他用户帮助他。如果有箭头相连，那么这两个用户间存在协作关系。将箭头替换为无向边，可得到三个连通分支。在协作通信网络中，定义联盟为通过协作形成的连通分支上的用户集合，记作S，且S⊂K。

图1 用户间协作关系例子Fig．1An example of cooperation among users

若分配给各用户一单位能量，当形成联盟S时，S内用户的能量集中起来进行调度分配，即有S单位能量供S内用户进行数据传输。对于一个联盟，其形成及维护需要用户间进行额外信息交换，将此类信息数据量抽象成联盟成本。设联盟成本为

α表示联盟成本与联盟大小之间关系。

定义1 在OFDM协作通信网络中，η(S)为联盟S的能量效率，即消耗S单位能量传输的有效数据总量

在功率分配矩阵P中，行表示用户功率分配情况。将P中与S中用户相关的行按原先顺序整合成一个新功率分配矩阵，记作PS。类似地，划去子载波分配矩阵I中与S中用户不相关的行和列，得到一个只和S有关的子载波分配矩阵，记作IS。其中，PS是一个S行N列矩阵，IS是一个S N阶方阵。由(1)，(2)，(5)和(8)可得，

对 k，l∈S，Pkn和 Plm均为 PS中元素，Ikknn和 Ilkmn均为IS中元素，因此η(S)与PS和IS有关。

定义2 将总联盟K分割成多个互不相交的小联盟，我们称之为对K的一个划分，得到的小联盟集合 C= {S1，S2，…，SC}为K的联盟结构，并满足

定义3 在OFDM通信网络中，联盟博弈模型由 K={1 ，2，…，K}和K上的集合函数v:2K→ℝ 组成，其中v(Ø)=0，记作 ( K ;v)。对于非空联盟S⊂K，v(S)为S的联盟值，即为S中用户通过协作获得的总收益。在这里，定义

其中

并且v(S)在S中用户间进行分配。

v(S)为满足一定限制条件下，通过在联盟内部分配子载波和功率得到的η(S)的最大值。当Ikknn=0时，k未用子载波n发送自己的数据，信噪比γkn=0，为表示方便，用 γk+n取代 γkn。

由(12)，已知IS求η(S)最大值是一个与(7)类似的带不等式约束的非凸最优化问题，这里结合SQP算法进行功率分配。将(12)转换为标准形式

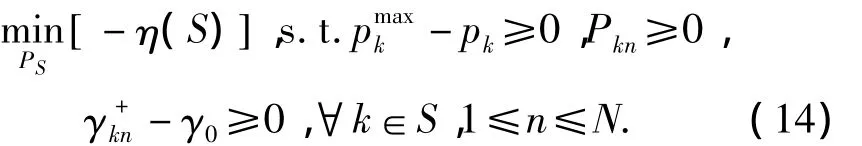
由于 pk，γk+n和η(S)均与 PS中元素有关，我们将PS中所有行按顺序整合成一个N S维向量x，表示联盟S中用户功率分配情况。f(x)表示－η(S)，用

表示(14)中(2N+1)S个不等式的左项，(14)即为

构造凸二次规划子问题

d为搜索方向，正定矩阵B∈ℝNS×NS为拉格朗日函数Hessian矩阵的近似。给定x，引入拉格朗日乘子构造广义拉格朗日函数求解得到最优搜索方向。先定义罚函数

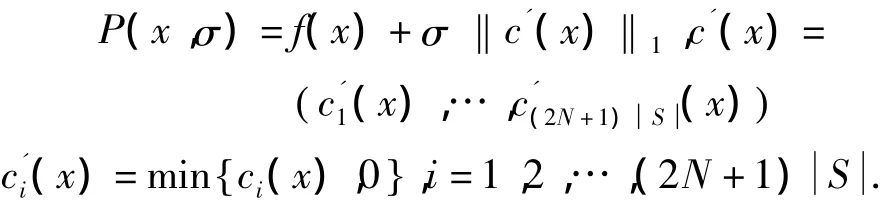
σ＞0为罚因子。下面给出具体功率分配算法:

1)取 x0∈ℝNS，δ＞0，σ ＞0，ε≥1，B0∈ℝNS×NS为正定矩阵，k=0。

2)xk和 Bk代入(17)求出 dk，若‖dk‖ ＜ ε，停止。

3)在[0，δ]内找到 αk，使得

上述算法将非凸问题转换成多次求解凸二次规划。B为正定保证了优化问题的凸性，求得的dk是唯一的。步骤5)运用了拟牛顿法中BFGS公式，迭代得到的新矩阵也能保证正定性。

特别注意，设置IS的取值时必须保证S是一个联盟(即S中用户通过协作形成的网络结构图是连通的)。后面我们在联盟合并算法中通过比较各种IS下η(S)的最大值，最终得到v(S)。

4． 2 联盟形成及合并算法

这里先给出联盟形成基本步骤:

1)初始化联盟结构为 {{1}，{2}，…，{K } }。

2)随机选取两联盟，若用户在合并形成的新联盟中支付均大于原先联盟内的支付，联盟进行合并，更新联盟结构;否则重新选择两联盟，进行上述操作。

3)若某个联盟结构中的所有联盟对都无法进行合并，停止。

对于步骤2)联盟合并的具体细节，将在后面联盟合并算法中详细给出。

定义4 对于联盟S中的用户k，其分配得到的支付为

Sk表示合并成S的两个联盟中包含k的联盟。

定理1 两个不相交的非空联盟S1和S2能够合并形成一个新的联盟，当且仅当

证明:令 S=S1∪S2，显然S≥2。由定义4，

要使S1和S2合并成一个新联盟，当且仅当对S1中任意用户k1和S2中任意用户k2，满足φk1(S)＞φk1(S1)和φk2(S)＞φk2(S2)(即所得支付均大于在先前联盟中的支付)，等价于

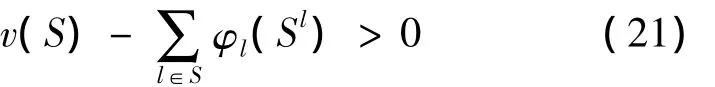
由(20)得到v(S1∪S2)－v(S1)－v(S2)＞0。证毕。

由于频率选择性衰落特性，用户与基站间基于不同子载波的信道增益值是不一致的，为表述简便，后面提到的增益都是基于用户与基站间的信道。如果用户将增益小的子载波用于发送自己的数据，在此子载波上分配较多功率也只能获得较低的传输率，而总功率有限，会影响到增益较大的子载波的传输率。哪怕用户在增益小的子载波上分配功率减少，也必须保证误码率性能。如果用户将增益小的子载波用于转发数据，其他用户也会乐意帮助该用户转发数据，因此增益小的子载波比增益大的子载波更适合转发数据。取常数g0，规定用户优先选择增益小于g0的子载波转发数据。对S1和S2组成的联盟对，下面给出联盟合并算法:

1)初始设置v=v(S1)+v(S2)。

2)取S1和S2中增益小于g0的1)类子载波最多的用户，记作k，不妨设 k∈S1，取 S2中增益大于g0的1)和2)类子载波最多的用户，记作l。

3)k选择一个增益小于g0的1)类子载波转发l的数据，通过SQP算法得到η(S1∪S2)。比较得到最大 η(S1∪S2)及对应 n 和 m，若 η(S1∪S2)＞v，令，v= η(S1∪S2)，更新 PS1∪S2和 IS1∪S2。

4)取S2中增益小于g0的1)类子载波数量最多的用户，记作k'，S1中增益大于g0的1)和2)类子载波数最多的用户，记作l'。

5)k'任选一个增益小于g0的1)类子载波转发l'的数据，通过SQP算法得到η(S1∪S2)。比较得到最大η(S1∪S2)及对应 n'和 m'，若 η(S1∪S2)＞v，令 Ik'n'k'n'=0，=η(S∪S)，更新 P和 I。12S1∪S2S1∪S2

6)随机配对S1和S2中用户(除k和l，k'和l')，按步骤3)进行，每次配对保证不重复，该步骤进行q次(q≤ S1S2－2)。

7)若v＞v(S1)+v(S2)，S1和S2合并成新联盟S1∪S2，令 v(S1∪S2)=v，更新联盟结构。

上述算法是在多种IS下调用SQP功率算法最终求解比较得出v(S):SQP功率算法是在求解最优功率分配矩阵，而联盟合并算法是在配置子载波分配矩阵。该算法说明了协作传输情形下的能量效率不低于非协作情形，因为每一次两个联盟合并后，整个网络的能量效率要更高一些。通过合理分配子载波和功率，有效提高了整个网络的能量效率。每个联盟可看作是一个通信子网，通过在内部合理分配子载波和功率使其能量效率更高。

5 结语

本文通过引入联盟博弈理论，以联盟概念描述用户间协作通信关系，通过引入一种联盟合并算法，有效解决了功率和误码率性能限制下的多用户OFDM通信网络能量效率优化问题:通过合理配置子载波分配矩阵和功率分配矩阵，使消耗相同能量下获得更大数据传输量。

［1］ COVER T，GAMAL A E L．Capacity Theorems for the Relay Channel［J］．IEEE Transactions on Information Theory，1979，25(5):572 －584．

［2］ 李易，邱玲，柳卫平．基于译码——转发的多中继协作节点选择方法［J］．通信技术，2010，43(04):56 －58．

LI Yi，QIU Ling，LIU Wei－ ping．Multi－ Relays Selection Scheme in Cooperative Networks Based on Decodeand － Forward Protocol［J］．Communications Technology，2010，43(04):56 －58．

［3］ HAN Z，HIMSOON T，SIRIWONGPAIRAT W P，et al．Energy－Efficient Cooperative Transmission over Multiuser OFDM Networks:Who Helps Whom and How to Cooperate［C］//Wireless Communications and Networking Conf－ erence，WCNC005．IEEE，2005，2:1030 －1035．

［4］ DRIESSEN T．Cooperative Games，Solutions and Appliations［M］．Dordrecht:Kluwer Academic Publishers，1988．

［5］ CHEN T，ZHU L，WU F，et al．Stimulating Cooperation in Vehicular ad Hoc Networks:A Coalitional Game Theoretic Approach［J］．IEEE Transactions on Vehic － ular Technology，2011，60(2):566 －579．

［6］ SIMON M K，ALOUINI M S．A unified Approach to the Performance Analysis of Digital Communication over Generalized Fading Channels［J］．Proceedings of the IEEE，1998，86(9):1860 －1877．

［7］ HAN S P．Superlinearly Convergent Variable Metric Algorithms for General Nonlinear Programming Problems［J］．Mathematical Programming，1976，11(1):263 －282．