PMC模型下的一个贪婪诊断算法*
2015-09-22宣恒农张润驰刘凌波
宣恒农,张润驰,何 涛,刘凌波
(1.南京财经大学信息工程学院,江苏 南京 210046;2.亚信科技(南京)有限公司,江苏 南京 210036)
PMC模型下的一个贪婪诊断算法*
宣恒农1,张润驰1,何 涛2,刘凌波1
(1.南京财经大学信息工程学院,江苏 南京 210046;2.亚信科技(南京)有限公司,江苏 南京 210036)
提出了一种PMC模型下基于矩阵运算的贪婪诊断算法——MGFD算法。算法结合作者曾经提出的“绝对故障基”思想,首先剔除绝对故障基,得到一个维度减小的矩阵,之后根据该矩阵求得集团。在文献[10]提出的四个贪婪诊断算法的基础上,提出集团的内贪婪因子、外贪婪因子、综合贪婪因子等概念,设计了新的贪婪准则。论证了 MGFD算法的正确性,并对算法进行了实验仿真。实验结果表明,MGFD算法相比文献[10]提出的贪婪诊断算法,具有较高的诊断正确率。
系统级故障诊断;PMC模型;绝对故障基;集团;贪婪诊断算法;综合贪婪因子;MGFD算法
1 引言
随着大数据时代的到来,计算机系统在社会生
活中扮演着越来越重要的角色,系统的可靠性和稳
定性也成为人们日益关心的话题。尤其是在军事、航天航空、电子商务等重要领域,系统发生故障经常会引起灾难性的后果,同时造成巨大的经济损失,因 此故 障规 避[1,2]与 模块冗 余[3]就成 了人们 解决这个问题的关键措施。然而,这两种措施在具体实现上、在控制系统成本和维护开销上,有很大的难度和一定的局限性。于是,通过测试、诊断来确定系统中故障单元的系统级故障诊断,就成为保证整个系统安全与稳定非常重要的手段。
对系统级故障诊断的研究是建立在故障模型基础之上的。当前主要的研究模型包括PMC (Preparata-Metze-Chien)模型[4]、BGM模型、Chwa&Hakimi模型与Malek模型等。其中,根据PMC模型的定义,任意一对互测单元的测试结果根据双方的故障状态分为四种情况:正常单元测试正常单元,其结果必为正常;正常单元测试故障单元,其结果必为故障;故障单元测试正常单元或故障单元,其结果可能为正常,亦可能为故障。设存在一个由有限个单元组成的系统X={x1,x2…xn},∀xi∈X,令xi=1表示xi正常,xi=—1表示xi存在故障,xi=0表示xi可能为正常,也可能为故障。令wij=1表示xi测试xj结果为正常,wij=—1表示xi测试xj结果为故障,wij=0表示xi对xj无测试。将全部这样的wij以i为行号、j为列号的规则存储在一个n行n列的矩阵A中,称矩阵A为系统X的一个测试症候矩阵。
系统级故障诊断近几年的主要研究成果包括基于图论 的 诊 断 算 法[5~10]和基 于 方 程 的 诊 断算法[11~14]两 大 类 。基于 图 论 的 诊 断算 法 将 测试 症 候矩阵与图论原理相结合,通过逻辑推导与图论运算,求出各单元的故障状态;基于方程的诊断算法将系统级故障诊断问题以方程的形式表现出来,通过对测试症候矩阵的方程运算求得相容解。相关理论分析与实验仿真均表明:当系统中故障单元数远小于总单元数的一半时,基于图论的诊断算法具有较高的诊断正确率,尤其是文献[10]提出的贪婪算法1,其诊断正确率接近100%,且时间复杂度不高;当系统中故障单元数远大于总单元数的一半时,基于图论的诊断算法正确率明显下降,此时文献[11~14]提出的基于方程的诊断算法具有较高的诊断正确率。然而,当故障单元数接近系统中总单元数的一半时,上述各算法均不能得到较为满意的诊断结果。本文在文献[9~12]的基础上,提出了一个在PMC模型下基于矩阵运算的贪婪诊断算法——MGFD(Matrix based Greedy Fault Diagnosis)算法。
MGFD算法主要分为三个步骤:首先,结合作者曾经提出的“绝对故障基”概念,通过剔除绝对故障基,降低测试症候矩阵的维数;接着,根据降维后的测试症候矩阵求出集团;最后,以提出的“综合贪婪因子”作为算法的贪婪准则,进行贪婪诊断。经实验验证,当系统中故障单元数接近一半时,MGFD算法具有明显的优越性。
2 贪婪诊断算法
根据诊断结果的精确程度,诊断算法可分为确定性诊断与概率性诊断两类。确定性诊断算法能够诊断出系统中的所有故障单元(完全诊断),且无正常单元被误诊断为故障单元(正确诊断),但往往具有较高的时间复杂度,且对系统的结构与连通度具有一定的要求;概率性诊断以牺牲诊断结果的精度为代价,换取诊断过程的低开销,同时诊断结果的正确性也保持在可接受的范围之内,从而提高算法的诊断能力,因此应用范围较广。贪婪诊断算法作为概率性诊断算法的一种,其特点是算法的每一次迭代均以当前信息为基础,根据某个贪婪准则作出当前最优选择,而不考虑各种后续步骤的情况,从而省去了为搜索全局最优解要穷尽所有可能而必须耗费的大量时间。每做一次选择,就将所求问题简化为一个规模更小的子问题,通过每一步的贪心迭代,得到问题的一个最优解。与其它诊断算法相比,贪婪诊断算法具有实现简单、时间复杂度低、诊断正确率较高等特点。
文献[9]提出了集团的概念:
对任一连通图G(U,E)(其中U为图中单元集,E为图中单元间边集),H叫做连通图G(U,E)的一个集团,当且仅当:
(1)H中如果多于一个单元时,H中任意两单元之间至少有一条权全为1/1的通路。
(2)对任意一个单元xi∈H,如果与H外的单元xj相邻接,则wij、wji不同时为0。
集团的性质1 集团H中的所有单元,要么同时为正常单元,要么同时为故障单元。
集团的性质2 正常集团的邻接集全部为故障集团。
文献[10]提出了四个基于集团理论的贪婪诊断算法,四个贪婪诊断算法的差别在于贪婪准则不同,这四个算法也同样适用于PMC模型。其中,算法1与算法2分别以各集团所含单元数目的大小作为算法的贪婪准则:算法1优先选取包含单元数最多的集团为正常集团,算法2优先选取包含单元数最少的集团为故障集团。算法3与算法4分别以各集团的相邻集团所含单元数目的大小作为算法的贪婪准则:算法3优先选取相邻集团包含单元数最少的集团为正常集团,算法4优先选取相邻集团包含单元数最多的集团为故障集团。四个贪婪算法中,算法1的诊断正确率相对最高。若记第i个集团为Hi,集团Hi的邻接集为C(Hi),Hi中的单元数目为|Hi|,则算法1的主要过程可表述如下:
步骤1 根据测试症候矩阵生成集团。
步骤2 识别绝对故障集团。
步骤3 对剩余集团按各自节单元数进行排序,设排序后满足|H1|≥|H2|≥…≥|Hi|。
步骤4 选择包含单元最多的集团为正常集团,其相邻基团置为故障集团。若存在两个集团|Hp|=|Hp+1|,设C(H')为 C(H)中 已 判 定 为 故 障 集 团 的 集 团,若|C(Hp)|—|C(H'p)|≤|C(Hp+1)|—|C(H'p+1)|,则置Hp为正常集团。
步骤5 若还存在未被确定状态的集团,重复步骤4;否则,算法结束。
3 MGFD算法的主要过程
3.1 剔除绝对故障基
文献[11]提出了绝对故障基的概念。同时,文献[12]给出了基于测试症候矩阵的绝对故障基求法。设A为一个n维PMC模型的测试症候矩阵,TA为关于A的绝对故障基(即包含所有必存在故障的单元的集合),则TA可按如下方式得到:
将A—A'中元素2所在行的行数代表的单元[11]合并组成TA。其中A'为A的转置矩阵。
在求得绝对故障基TA后,将测试症候矩阵A中各绝对故障单元所在的行、列删除,得到不包含绝对故障单元的症候矩阵B。矩阵B相对于测试症候矩阵A降低了维数,减少了后续运算的数据量。
3.2 求集团
文献[9]提出了一种求集团的算法,该算法的时间复杂度为O(n2)。在求得各集团后,将各集团中所有的点归并为一个集团点,按矩阵B中的连接方式相连,形成集团间的测试矩阵C。
3.3 设计贪婪准则
概率性诊断算法以“相信大多数”作为基本诊断原理,即“相信系统中大多数单元为正常单元,从而接受大多数单元的测试结果”。若与集团的思想相结合,其诊断原理可引申为:某一集团所含单元数越多,且其邻接集包含的单元数越少,该集团为正常集团的可能性越大。假设系统中各单元是否出现故障是随机且相互独立的,系统中每一单元xi出现故障的概率为p,该系统可根据矩阵B划分为若干个集团,对其中的任一 集团Hi,用ni表示集团Hi所含单元的数目,mi表示集团Hi的邻接集C(Hi)中各集团所含单元数之和,P(Hi=1)表示Hi为正常集团的概率,P(C(Hi)=—1)表示Hi的邻接集所含集团均为故障集团的概率。在不考虑各集团中实际连接边数等前提下,可将“相信大多数”的诊断原理归纳为以下两个诊断准则:
诊断准则1 对任意两个集团Hi、Hj,若mi=mj且ni>nj,则P(Hi=1)>P(Hj=1)。
诊断准则2 对任意两个集团Hi、Hj,若ni= nj且mi>mj,则P(Hi=1)<P(Hj=1)。
证明 先暂不考虑各集团邻接集的存在。根据集团的性质1,对任一集团 Hi,若其为故障集团,则集团中的每个单元均为故障单元,又由于系统中各单元是否出现故障是随机且相互独立的,有Hi为故障集团的概率为pmi;又由于“Hi为故障集团”与“Hi为正常集团”构成一对对立事件,其概率和为1,故Hi为正常单元的概率为
现考虑存在邻接集的情况。根据集团的性质2,可知对任一集团Hi,Hi与C(Hi)的故障分布只可能有以下三种情况:Hi为正常集团且C(Hi)为故障集团、Hi为故障集团且C(Hi)为正常集团、Hi与C(Hi)均 为 故 障 集团。此 时,有,同理,对集团Hj,有由于p∈(0,1),当mi=mj, ni>nj时,故P(Hi= 1)>P(Hj=1),诊断准则1得证;当ni=nj,mi> mj时,因为,故P(Hi= 1)<P(Hj=1),诊断准则2得证。
由于贪婪诊断算法按照贪婪准则,每做一次贪婪选择后,结果不可改变,后一次贪婪选择在前一次贪婪选择结果的基础上进行,因此算法诊断效果的好坏主要与算法的贪婪准则选取有关。较好的贪婪准则使得算法具有较好的爬坡能力,能够得到与最优解十分近似的较优解。我们结合文献[10]提出的四个贪婪诊断算法的诊断思想与概率性诊断的诊断准则1、诊断准则2,对贪婪准则进行优化,以“综合贪婪因子”作为算法的贪婪准则,兼顾了各集团本身所含单元数目与邻接集中单元数目对贪婪准则的综合影响。
首先,给出对每一集团Hi的内贪婪因子αi、外贪婪因子βi与综合贪婪因子gre_index[i]的定义:
集团Hi的内贪婪因子αi=f(ni);
集团Hi的外贪婪因子βi=g(ni,mi);
集团Hi的综合贪婪因子gre_index[i]=αi* βi;
其中,f(·)为ni正相关的函数,g(·)为与ni正相关、与mi负相关的函数。内贪婪因子αi体现的是诊断准则1对贪婪准则的影响,外贪婪因子βi体现的是诊断准则2对贪婪准则的影响。显然,综合贪婪因子越大,则该集团为正常集团的概率亦越大。
我们对若干组不同的f(·)、g(·)目标函数(包括取线性、指数、对数等)进行了组合实验,选取了一个实验结果最好的综合贪婪因子目标函数:
αi=f(ni)=log ni,βi=g(ni,mi)=ni/mi,综合贪婪因子:

结合式(1),显然对任意ni>0,mi>0,我们有:

即gre_index[i]为关于ni的递增函数,亦为关于mi的递减函数。对任意两集团Hi、Hj,若mi=mj且ni>nj,有gre_index[i]>gre_index[j],即P(Hi=1)>P(Hj=1),符合诊断准则1;若ni=nj且mi>mj,有gre_index[i]<gre_index[j],即P(Hi=1)<P(Hj=1),符合诊断准则2。
在划分出各集团之后,分别求出各集团的综合贪婪因子gre_index[i],接着以综合贪婪因子作为算法的贪婪准则,进行集团的划分。
4 算法步骤与效率分析
在上一部分的基础上,我们将 MGFD算法的完整步骤总结如下:
输入:测试症候矩阵A。
输出:各单元的经诊断的故障状态。
步骤1 按文献[12]的方式,通过A—A'运算,求得绝对故障基TA。
步骤2 将测试症候矩阵A中各绝对故障单元所在的行、列删除,得到矩阵B。
步骤3 根据矩阵B,求得集团,并得到集团连接矩阵。
步骤4 按式(1)求出各集团的综合贪婪因子,对输入的各集团按综合贪婪因子从大到小排序,结果存储在队列Q中,并初始化各集团故障状态值,统一置为0。
步骤5 取Q中的队列头部(以下简称“队头”)集团,若队头集团的状态值为0,则将该集团判断为正常集团,同时其邻接集中各集团判断为故障集团;否则(队头集团已被判断),重复步骤5。
步骤6 若队列非空,重复步骤5;否则,继续步骤7;
步骤7 将各集团的诊断结果映射为各单元的诊断结果,同时与步骤1求得的绝对故障基结果相结合,得到所有单元的诊断结果,并输出。
显然,上述七个步骤顺序执行,则最复杂步骤的时间复杂度代表了算法的整体时间复杂度。其中,步骤1与步骤3的时间复杂 度最大,均为O(n2),故算法的整体时间复杂度为O(n2)。
5 实验仿真
文献[10]对提出的四个贪婪诊断算法进行了实验仿真,其实验结果表明:在相同参数条件下,贪婪算法1的诊断正确率远高于其它三个贪婪算法,故我们只与贪婪算法1进行比较。为便于比较,所选测试图与文献[10]一致,均为k-正则图。实验参数完全采用文献[10]中的设置:单元总数均为100,故障单元随机产生,故障单元数从1到60变化,对每一种组合,各做1 000次实验,取其平均诊断正确率。
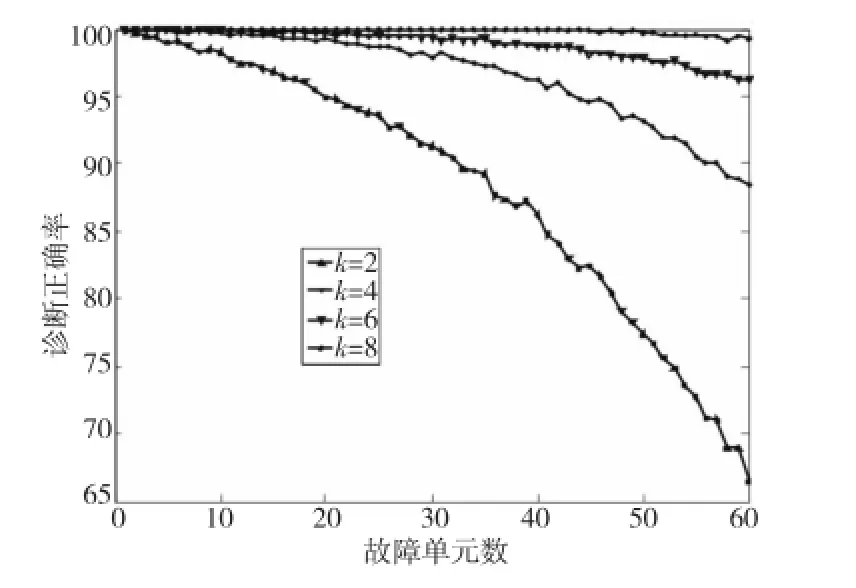
首先,我们分别在连通度为2、4、6、8的随机生成测试图中对 MGFD算法的诊断效果进行了独立实验,MGFD算法在不同连通度下的诊断正确率如图1所示。
接着,我们对MGFD算法与文献[10]提出的贪婪算法1分别在不同连通度的随机测试图中进行了比较实验。图2a、图2b、图3a、图3b分别展示了两个算法在连通度为2、4、6、8时的诊断正确率。
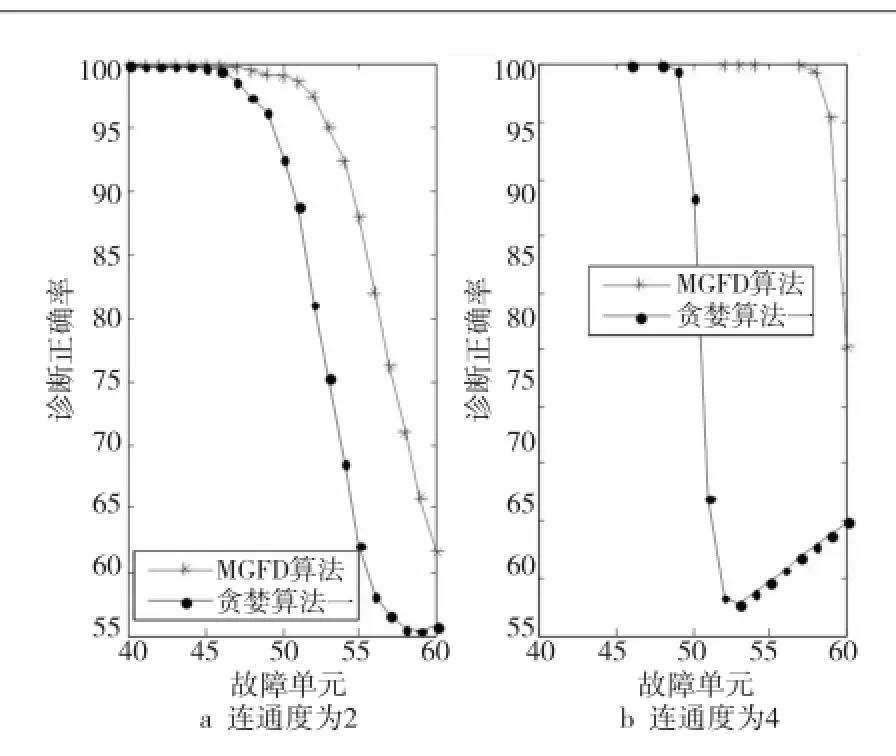

分析以上的实验结果,我们得到如下的结论:
(1)在同一个测试图中,当故障单元数较少时,MGFD算法与贪婪算法1的诊断正确率均接近100%;当故障单元数约为系统中单元总数一半左右时,MGFD算法的诊断正确率明显高于文献[10]提出的贪婪算法1。
(2)当系统中单元数目固定时,随着系统连通度的上升,更多的故障单元可能被检测出属于绝对故障基,或表现出更明显的故障特征,测试症候矩阵所含信息价值更大,因此集团的划分愈精确,MGFD算法的诊断正确率逐渐升高。
(3)在相同的系统中,随着故障单元数目的上升,MGFD算法的诊断正确率逐渐降低,但在高连通度的系统中算法诊断正确率降低的幅度明显小于在低连通度系统中降低的幅度。
实验表明了当系统中故障单元数目较少时,MGFD算法的诊断正确率接近100%;当故障单元数目接近系统中总单元数的一半时,MGFD算法相比较于贪婪算法1,确实具有优越性。
6 结束语
本文提出了一个在PMC模型下基于矩阵运算的贪婪诊断算法——MGFD算法。算法适用于高维诊断模型与故障单元数目接近系统中总单元数的一半时的情形。
算法首先剔除绝对故障基,再求集团,由此降低了测试症候矩阵的维数,进而提高了诊断效率,因此尤其适用于高维诊断模型。同时,相关研究表明:当故障单元数目接近系统中总单元数的一半时,基于图论的诊断算法与基于方程的诊断算法均不能取得让人较为满意的诊断结果。MGFD算法有机地结合了图论诊断与方程诊断的部分思想,设计出基于综合贪婪因子的贪婪准则。实验表明,当故障单元数较少时,MGFD算法的诊断正确率能够达到100%;当故障单元数目接近系统中总单元数的一半时,诊断正确率随着网络连通度的提高而逐渐上升,且始终高于现有的贪婪诊断算法。
MGFD算法不仅适用于PMC模型,只要根据特定模型的特性,对该算法稍作修改,即可应用于BMG模型、Chwa&Hakimi模型和Malek模型,因篇幅所限,在此不再赘述。接下来的研究主要有综合贪婪因子合适目标函数的定量选取,基于高维诊断模型的实验仿真等。
[1] Sun Y,Chen M,Liu B,et al.FAR:A fault-avoidance routing method for data center networks with regular topology[C]∥Proc of 2013 ACM/IEEE Symposium on Architectures for Networking and Communications Systems(ANCS),2013:181-189.
[2] Amagasaki M,Inoue K,Zhao Q,et al.Defect-robust FPGA architectures for intellectual property cores in system LSI[C]∥Proc of 2013 the 23rd International Conference on Field Programmable Logic and Applications(FPL),2013:1-7.
[3] Yin P Y,Chen Y H,Lu C W,et al.A multi-stage fault-tolerant multiplier with triple module redundancy(TMR)technique[C]∥Proc of 2013 the 4th IEEE International Conference on Intelligent Systems Modelling&Simulation(ISMS),2013:636-641.
[4] Preparata F P,Metze G,Chien R T.On the connection assignment problem of diagnosable system[J].IEEE Transactions on Electronic Computer,1967,16(12):848-854.
[5] Falcon R,Almeida M,Nayak A.A binary particle swarm optimization approach to fault diagnosis in parallel and distributed systems[C]∥Proc of 2010 IEEE Congress on Evolutionary Computation(CEC),2010:1-8.
[6] Elhadef M.Solving the PMC-based system-level fault diagnosis problem using hopfield neural networks[C]∥Proc of 2011 IEEE International Conference on Advanced Information Networking and Applications(AINA),2011:216-223.
[7] Srivastava H O,Gupta S C.Effect of fault patterns on systems level diagnosis of mesh networks[C]∥Proc of 2013 the 10th International Conference on Wireless and Optical Communications Networks(WOCN),2013:1-4.
[8] He Q Y,Qiu J,Liu G J,et al.System-level BITs fault diagnosis and isolation based on diagnostic tree and Bayesian network[J].Key Engineering Materials,2014(584):102-106.
[9] Zhang Da-fang,Xie Gao-gang,Min Ying-hua.Node grouping in system-level fault diagnosis[J].Journal of Computer Science&Technology,2001,24(5):474-479.
[10] Liu Bing,Zhang Da-fang,Duan Zhi-yong.A probabilistic algorithm of system-level fault diagnosis based on greedy principle[J].Acta Electronica Sinica,2004,32(8):1360-1363.(in Chinese)
[11] Xuan Heng-nong,Zhang Da-fang,Zhang Ming.PMC fault model diagnostic equation[J].Acta Electronica Sinica,2003,31(5):694-697.(in Chinese)
[12] Xuan Heng-nong,Han Zhong-yuan,Zhang Da-fang.PMC model-based fault diagnosis method and its application[J]. Acta Electronica Sinica,2007,35(5):987-990.(in Chinese)
[13] Xuan Heng-nong.On the system-level fault diagnosis[J]. Computer Engineering,2001,27(4):12-13.(in Chinese)
[14] Wen Xue-zhi,Xuan Heng-nong,Xu Hong.An application of equation diagnosis algorithm in Malek fault models[J]. Computer Engineering,2006,32(1):46-47.(in Chinese)
附中文参考文献:
[10] 刘兵,张大方,段智勇,等.基于贪婪算法的系统级故障的概率诊断[J].电子学报,2004,32(8):1360-1363.
[11] 宣恒农,张大方,张明.PMC故障模型的方程诊断[J].电子学报,2003,31(5):694-697.
[12] 宣恒农,韩忠愿,张大方.基于互测PMC模型的故障诊断方法及其应用[J].电子学报,2007,35(5):987-990.
[13] 宣恒农.关于系统级故障诊断[J].计算机工程,2001,27 (4):12-13.
[14] 文学志,宣恒农,许宏.方程诊断算法在Malek故障模型中的应用[J].计算机工程,2006,32(1):46-47.

宣恒农(1958 ),男,江苏淮安人,教授,研究方向为系统级故障诊断、未来网络和符号计算。E-mail:13913891389@163. com
XUAN Heng-nong,born in 1958,professor,his research interests include system-level fault diagnosis,future network,and symbol computing.

张润驰(1990 ),男,江苏南京人,硕士,研究方向为系统级故障诊断、数据挖掘和量化交易。E-mail:zhangrunchi@ aliyun.com
ZHANG Run-chi,born in 1990,MS, his research interests include system-level fault diagnosis,data mining,and quantitative trading.

何涛(1983),男,河南郑州人,硕士,软件工程师,研究方向为系统级故障诊断和符号计算。E-mail:hetao.1983@yahoo. com.cn
He Tao,born in 1983,MS,software engineer,his research interests include system-level fault diagnosis,and symbol computing.

刘凌波(1973 ),女,河南商丘人,硕士,副教授,研究方向为系统级故障诊断和符号计算。E-mail:djbllb@126.com
LIU Ling-bo,born in 1973,MS,associate professor,her research interests include system-level fault diagnosis,and symbol computing.
A greedy diagnosis algorithm for PMC model
XUAN Heng-nong1,ZHANG Run-chi1,HE Tao2,LIU Ling-bo1
(1.School of Information Engineering,Nanjing University of Finance and Economics,Nanjing 210046;
2.AsiaInfo Linkage Technology Co.,Ltd.Nanjing Branch,Nanjing 210036,China)
We propose a greedy diagnosis algorithm based on the matrix operations called Matrix based Greedy Fault Diagnosis(MGFD)algorithm under the PMC model.With the“absolute fault base“concept put forward by the authors in paper[11],we remove the absolute fault units to obtain a matrix of reduced dimensions and then get the groups accordingly.On the base of the four existing greedy diagnostic algorithms proposed by paper[10],we define the concepts of inner greed factors,outer greed factors,comprehensive greed factors of each group,and we also design some new greedy criteria.We demonstrate the correctness of the MGFD algorithm,and design several simulation experiments for the algorithm.Experimental results show that the MGFD algorithm has a higher diagnostic accuracy in comparison with the existing greedy diagnostic algorithm proposed by paper[10].
system-level fault diagnosis;PMC model;absolute failure base;group;greedy diagnosis algorithm;comprehensive greedy factor;MGFD algorithm
TP301
A
10.3969/j.issn.1007-130X.2015.08.003
1007-130X(2015)08-1430-06
2014-08-11;
2014-10-15
国家自然科学基金重大研究计划资助项目(90718008);国家自然科学基金重点项目(61133015);江苏省自然科学基金资
助项目(2004119)
通信地址:210046江苏省南京市南京财经大学信息工程学院
Address:School of Information Engineering,Nanjing University of Finance and Economics,Nanjing 210046,Jiangsu,P.R.China
