直流偏磁时变压器铁芯的力学特性分析
2015-09-21李长云刘亚魁
李长云,刘亚魁
(齐鲁工业大学 电气工程与自动化学院,山东 济南 250353)
0 引言
大型变压器的直流偏磁现象是指由于高压直流输电工程单极大地运行方式时的地中直流[1-2]、太阳风在地球表面引发的地磁感应电流(GIC)[3-4]等致使变压器绕组中出现直流电流。直流偏磁将引起变压器铁芯出现半周饱和[5],使得变压器局部过热,铁芯、绕组振动和噪声加剧[6],甚至损坏变压器[7]。 当前文献对变压器直流偏磁现象的研究主要集中于以下几方面:直流偏磁时变压器励磁电流及振动的测量[6,8-9];直流偏磁时铁芯的磁化特性及变压器的数学模型[10-11];变压器承受直流偏磁的能力[12-13];直流偏磁的抑制措施[14-15]等。尚未有文献对直流偏磁时变压器噪声和振动加剧的原因进行深入分析。
就变压器的振动和噪声而言,其铁芯在磁场中受到的磁致伸缩力是其振动与噪声产生的根源[16-17]。正常工况时,变压器处于正弦交变的电场中,绕组所受到的电场力可将电磁场理论和弹性力学相结合推导得出[18];文献[19]基于铁芯的 Jiles-Atherton 模型,结合能量守恒定律研究了变压器铁芯的磁致伸缩特性。因以上文献均未考虑直流偏磁的影响,其结论能否直接应用于偏置情况尚需加以推敲。同时,变压器铁芯振动亦对其油纸绝缘系统中绝缘纸的绝缘强度有重要影响[20]。因此,为研究变压器的振动与噪声的抑制措施、明晰变压器承受的直流偏磁电流的能力,以指导变压器的设计与运行,需深入探析偏置电场中变压器铁芯的力学特性。
本文以变压器铁芯的单片硅钢片为研究对象,基于电磁场理论和能量守恒定律,研究了直流偏磁时变压器铁芯所受磁致伸缩力,获得了它与直流偏磁电流的量化模型,并利用仿真分析对所得模型的正确性进行了佐证。
1 磁致伸缩的数学模型
其中,N为线圈匝数;i为注入电流;l为磁路长度;iac、idc分别为交流电流和直流电流;Hac、Hdc分别为交流磁场强度和直流磁场强度。
磁致伸缩是铁磁材料励磁时,沿磁力线方向材料的尺寸增加,而垂直于磁力线方向材料的尺寸缩小。磁致伸缩引发铁芯以2倍的励磁频率作周期性振动。当长度为L的磁性材料在磁化方向上的长度变化为ΔL时,磁致伸缩率可表示为:

变压器绕组中有偏磁电流时将形成偏置电磁场,建立铁芯磁场力的数学模型是探析铁芯振动的基础。由全电流定律知,直流偏磁时的磁场强度为:
其中,λ0为磁致伸缩率;ΔL为最大形变。由式(2)可看出,硅钢片磁致伸缩率越大,硅钢片的最大形变就越大,则铁芯的振动越剧烈。从能量守恒和功能转换的角度,磁致伸缩率实际是材料的最大应变,结合弹性力学理论,弹性体发生形变时,单位体积的应变能为:
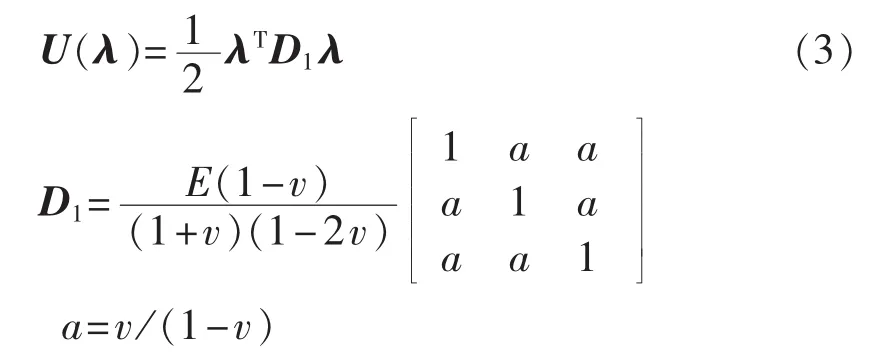
其中,λ=[λxλyλz]T为 x、y、z方向的磁致伸缩率组成的矩阵;E为材料的弹性模型;v为材料的泊松比;D1为弹性关系矩阵。
当偏置磁场达到峰值时,介质的磁致伸缩率同时达到峰值,对应的应变能最大。本文在如图1所示硅钢片的坐标系中,规定z方向与其所受的磁致伸缩力方向一致,故仅考虑z方向的形变,可推得式(4)。
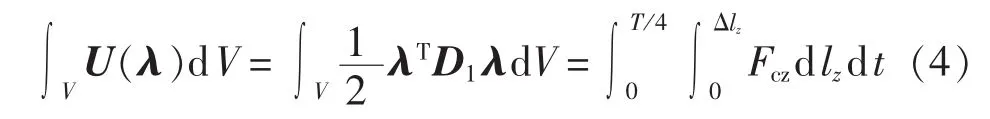
其中,V为介质的体积;T为正弦磁场周期;因λ是线应变,则 dlz=λzdz。
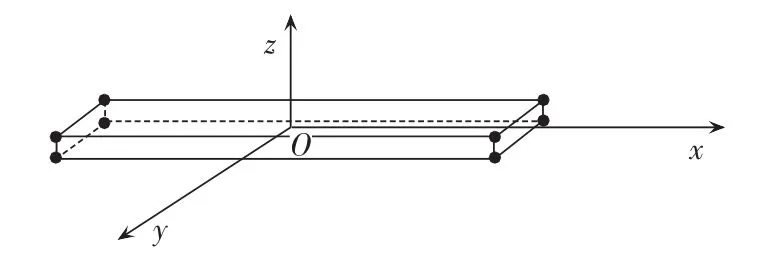
图1 硅钢片的坐标系Fig.1 Coordinates of silicon steel
故磁致伸缩可简化为:
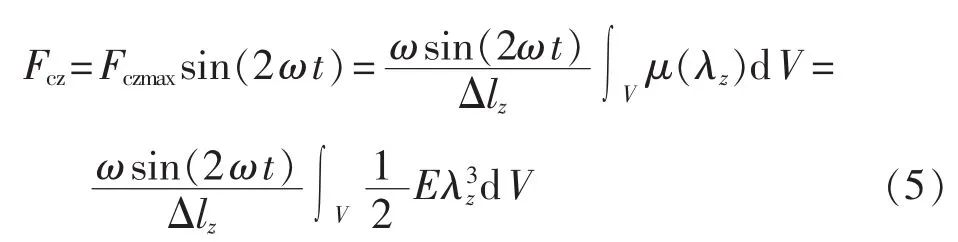
基于以上磁致伸缩的模型,便可分析直流偏磁时铁芯的受力情况。
2 偏置电场中铁磁材料的形变
变压器工作于直流偏磁状态时,其铁芯的磁化特性呈半周饱和现象。为研究铁芯的最大形变,取磁通密度最大时的铁芯作为研究对象。

其中,D0=Et3/[12(1-v2)]为板的弯曲刚度;t为板的厚度;q(x,y)为作用在板表面z方向的分布载荷。
铁芯的磁致伸缩率随磁通密度的增大而增大,而偏磁电流产生的直流磁场会显著升高磁通密度。为研究铁芯的最大形变,取磁通密度最大时的磁致伸缩率作为研究对象。
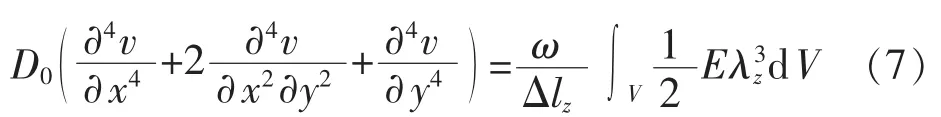
进而可推导出表征磁致伸缩的磁场力模型为:

据式(8)即可求解出不同直流偏磁时磁致伸缩诱发的铁芯形变。根据硅钢片在变压器中的紧固方式,可以确定边界条件为两端固支,而另外两端为自由边。
3 仿真研究
为了验证本文所得出的结论,以单相三柱变压器旁柱上最外层硅钢片为研究对象进行仿真研究,具体参数如表1所示。硅钢片长度为300 mm,宽度为 25 mm,厚度为 0.3 mm;材料特性 E=2×1011Pa,v=0.25;励磁条件为标称额定磁通密度1.6T,励磁频率为50 Hz。
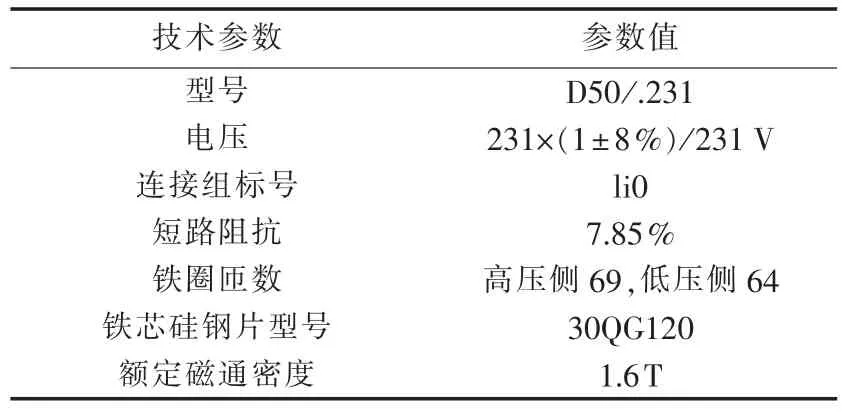
表1 单相变压器参数Table 1 Parameters of single-phase transformer
对于30QG120型硅钢片,建立不同偏磁电流下,铁磁材料的磁致伸缩率变化如图2所示。
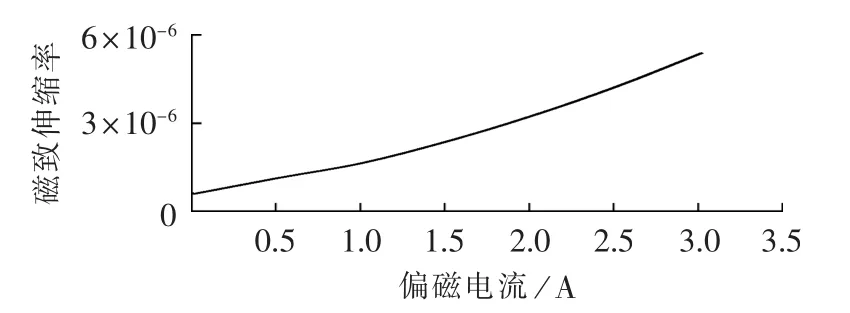
图2 磁致伸缩率与偏磁电流的关系Fig.2 Relationship between magnetostriction rateand DC-bias current
当直流电流 Idc分别取 0 A、0.5 A、1 A、1.5 A、2 A、2.5 A和3 A时,对硅钢片进行仿真。所得结果如图3、4所示,最大形变示于表2中。
由图3、4及表2知,无偏磁电流时,本文计算所得磁致伸缩引发的形变为3.9×10-6m,与文献[21]所实测结果4.5×10-6m非常接近。同时,偏磁电流由0增加为1A时,其形变增大7.4倍,即直流偏磁能显著影响硅钢片的振动。且偏磁电流越大,磁致伸缩现象越严重,铁芯振动越剧烈。
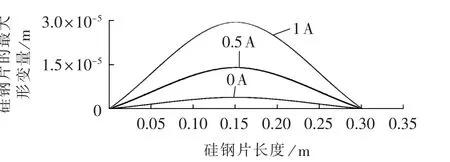
图3 Idc为0、0.5、1 A时,硅钢片的最大形变量Fig.3 Maximum silicon steel deformationfor Idcis 0 A,0.5 A and 1 A
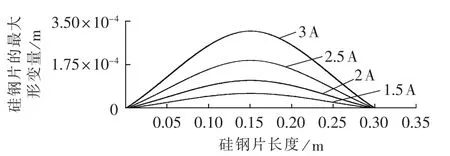
图4 Idc为 1.5、2、2.5、3 A 时,硅钢片的最大形变量Fig.4 Maximum silicon steel deformation for Idcis 1.5 A,2 A,2.5 A and 3 A

表2 不同偏磁电流时,磁致伸缩引发的硅钢片最大形变Table 2 Maximum silicon steel deformation caused by magnetostriction for different DC-bias currents
4 结论
本文基于能量守恒原理,推导了直流偏磁时磁致伸缩的量化表达式。理论分析表明,直流偏磁电流加剧了变压器铁芯的振动,且偏磁电流越大,其所引发的振动越明显。
