基于局部均值分解的同步电机参数辨识方法
2015-09-21黄传金陈铁军张国志宋海军
黄传金,陈铁军,张国志,宋海军,罗 勇
(1.中州大学 机电与汽车工程学院,河南 郑州 450044;2.郑州大学 电气工程学院,河南 郑州 450001;3.河南送变电工程公司,河南 郑州 450052)
0 引言
同步电机是电力系统中的重要设备,其参数对于电力系统运行和控制至关重要[1-2]。GB/T1029—2005推荐使用的同步电机参数测量方法是三相突然短路法。传统方法是通过短路电流上、下包络线的加减运算提取周期性分量和非周期性分量,再通过最小二乘曲线拟合的方法获取瞬态参数,该方法辨识结果误差较大[3]。一般用指数函数来表示突然短路电流,而Prony算法适合指数函数的参数辨识,应用Prony算法辨识同步电机参数的效果较好[4],但Prony算法对噪声较敏感。
噪声对同步电机参数辨识的精度影响较大。为提高辨识的精度,常先滤除噪声,然后再结合辨识算法辨识同步电机参数。如小波变换和Prony算法[3]、矩阵束[5]、神经网络[6]等相结合的同步电机参数辨识算法。这种方法预先滤除了噪声信号,在低信噪比(如20 dB)时也能取得较高的参数辨识精度,但小波变换不仅受Heisenberg测不准原理的制约,还存在基函数选取问题,缺乏自适应性[7]。运用经验模态分解EMD(Empirical Mode Decomposition)获取同步电机电流中的直流分量和基波电流,进而辨识同步电机参数,较好地解决了连续高频噪声时参数辨识精度较低的问题[7-8],但EMD存在模态混叠问题。
局部均值分解LMD(Local Mean Decomposition)是一种新的非线性信号分析方法[9]。和EMD类似,LMD也是根据信号的包络特征自适应地将信号按频率从高到低的顺序依次分离出若干个瞬时频率具有物理意义的乘积函数PF(Product Function)分量,由PF可重构原始信号。较之EMD,LMD具有分解速度快、端点效应好等优点[10-12]。目前,在电力工程信号中,LMD主要用于分析电能质量[10-11]和电力系统低频振荡[12]信号。但上述文献均没有分析含有噪声信号时LMD的性能;另外LMD的滑动平均跨度选择还需进一步研究[10-12]。
本文提出了基于LMD的同步电机参数辨识新方法,结合突然短路电流,通过仿真选取了最佳的滑动平均跨度;在电流信号分别含有高信噪比(30 dB)、随机的低信噪比(15 dB)和连续的高频噪声时采用LMD有效地提取了直流分量和基波电流;然后对其分别采用稳健回归最小二乘和Prony算法辨识同步电机参数,仿真和实验结果证明了本文所提方法的可行性和有效性。
1 LMD算法流程和Prony算法
1.1 LMD算法流程
局部均值分解本质上根据信号固有的包络特征自适应地将一个非线性、非平稳信号按频率递减的顺序逐级分离[11,13]。LMD的分解过程是一个三重循环过程:第一重循环为滑动平滑求取局域均值函数min(t)和包络估计函数 ai(t),循环终止条件滑动平滑后信号的相邻点均不相等;二重循环为求取PFi(t)的过程,循环终止条件为求取出来的sin(t)为纯调频信号;第三重循环为求取所有PFi(t)的过程,循环终止条件为残余分量uk(t)有且只有1个极值点。经过3次循环从原始信号中分离出纯调频信号和包络信号,将纯调频信号和包络信号相乘求出第1个PF分量,然后再逐步循环处理,分解出所有的PF分量,进一步求出瞬时频率和瞬时幅值,便可以得到原始信号完整的时频分布。对于任一信号x(t),LMD的基本计算流程图如图1所示。
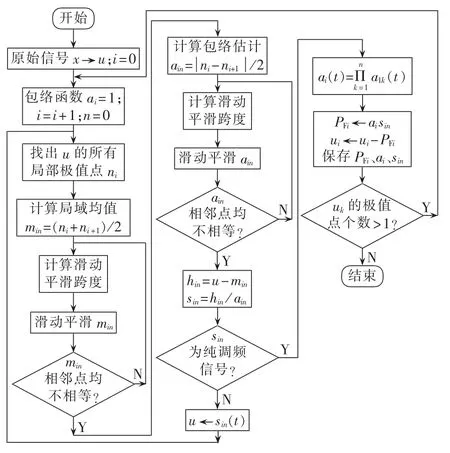
图1 LMD的基本计算流程Fig.1 Basic calculation process of LMD
通过LMD,信号x(t)被分解为下列形式:
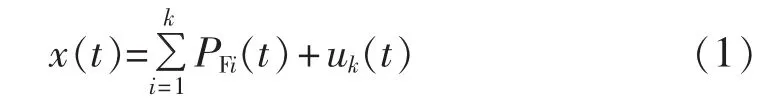
其中,PFi为调频调幅函数;k为PFi的个数;uk为残差。
1.2 Prony辨识算法
Prony算法假设离散的数字序列信号可用指数函数的线性组合表示,则有:

其中,Ai为幅值;Bi为留数;θi为初始相位;αi为衰减因子;ωi为角频率;Δt为采样间隔。
利用Prony算法辨识式(2)所示的指数模型参数需要以下 4 个步骤[4]。
a.构造线性预测模型。将x(k)用线性预测方程描述为:

该线性预测模型的拟合模型可由采样数据获得:
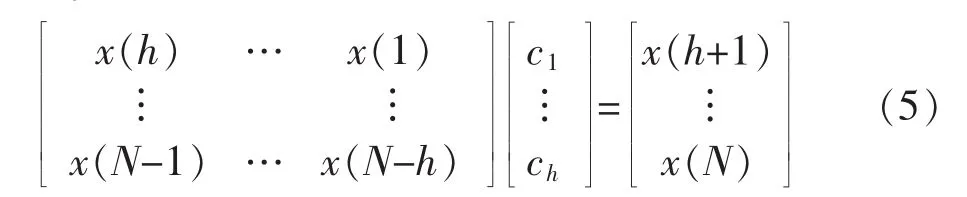
采用奇异值分解求解式(5),以得到拟合系数c1、c2、…、ch。
b.求解线性模型方程的特征根。
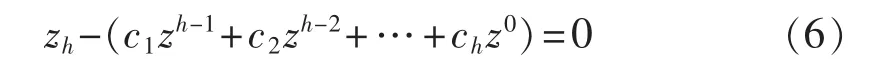
其中,特征根 zi=e(αi+jωi)Δt(i=1,2,…,h)。
c.计算留数。由式(5)可得:

对上式运用最小二乘法求解可得Bi。
d.求解各分量相位、幅值、衰减因子和频率。计算出反映各分量特征的量,计算式为:
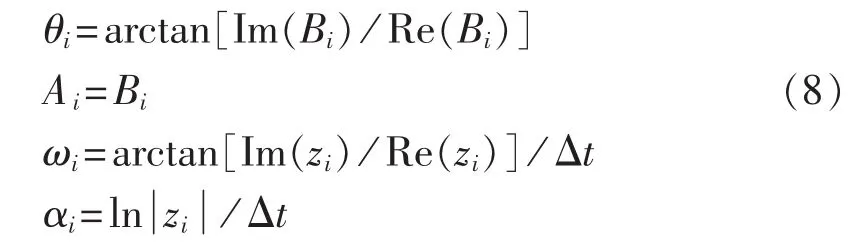
其中,i=1,2,…,h。
2 基于LMD的同步电机参数辨识
2.1 LMD滑动平均跨度选择
滑动平均的跨度不仅关系到LMD精度,如果滑动平均跨度选择不合理,有可能造成LMD算法不收敛[10,12]。 为求出最佳的滑动平均跨度,本文假设:电枢时间常数Ta=0.105s;直轴瞬态时间常数T′d=0.25 s,直轴超瞬态时间常数T″d=0.225 s;直轴电抗xd=1.169 p.u.,直轴暂态电抗 x′d=0.034 p.u.,直轴次暂态电抗x″d=0.18 p.u.;交轴次暂态电抗x″q=0.2 p.u.;短路时转子位置φ0=π/6;定子激磁电动势E=1 p.u.。然后将参数代入突然短路电流公式[3]:

其中,i0为直流分量;i2ω为 2次谐波分量;iω为基波分量;e(t)为噪声电流。
由式(9)得到的仿真电流如图2所示。运用镜像拓延消除端点效应,取Δe=0.001,通过仿真分析滑动平均跨度与循环次数的关系,用相对均方误差[3]来定量描述本文提取电流和理论电流的误差值。

图2 仿真的短路电流Fig.2 Simulative waveforms of short circuit current
循环次数与滑动平均跨度的关系如图3所示;相对均方误差与滑动平均跨度的关系如图4所示。由图3可知循环次数随滑动平均跨度的增加而增大;从图4可知滑动平均跨度为3和5时,基波和直流分量的相对均方误差较大;滑动平均跨度为7、9、13和15时,基波和直流分量的相对均方误差变化不大;但基波包络的相对均方误差随滑动跨度的增大而增加。综合以上因素,平均跨度可定为7。
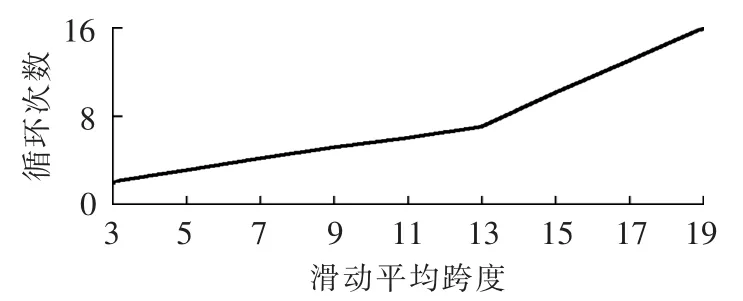
图3 滑动平均跨度与循环次数的关系图Fig.3 Relationship between moving average span and cycle
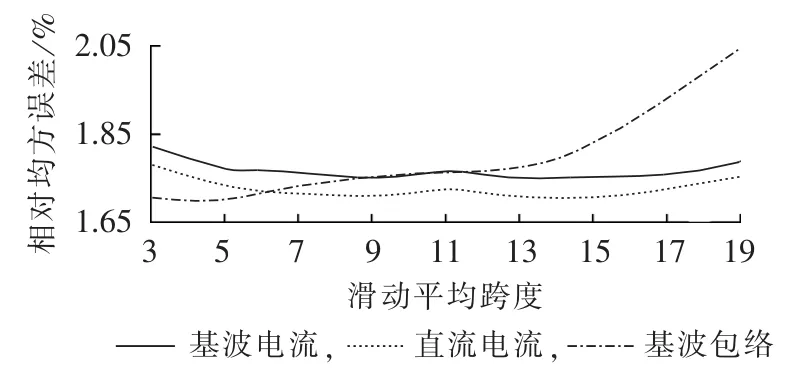
图4 滑动平均跨度与相对均方误差的关系图Fig.4 Relationship between moving average span and relative mean square error
图5为LMD和希尔伯特-黄变换(HHT,采用Rilling编写的程序,参数取默认值)分析上述信号时提取的基波电流、直流电流、基波频率和基波包络的对比图。从图5(a)、(b)可知LMD将短路电流仅分解为1个PF分量和残差信号,而HHT将其分解为2个固有模态函数(IMF)和残差信号;其中PF1可认为是基波分量,残差信号uk可作为直流分量,c1可作为基波电流成分,将c2与残差信号相加可得直流分量。2种方法获取的直流分量与理论值的对比图如图5(c)所示,由图可见,2种方法获取的直流分量与理论值很接近;较之HHT方法,LMD方法仅通过1次PF分离过程就可获取直流分量,而且LMD获取的直流分量在初始阶段波动较小。从图5(d)、(e)可知LMD方法获取的基波包络和基波频率波动较小、初始阶段的端点效应较小。
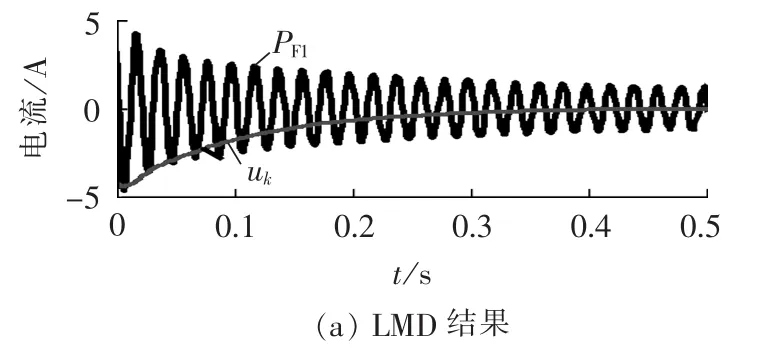

图5 基于LMD、HHT的短路电流分析对比图Fig.5 Comparison of short circuit current analysis between LMD and HHT
2.2 不同噪声时应用LMD提取基波和直流电流
2.2.1 高信噪比(30 dB)时基波和直流电流的提取
因滑动平均具有滤波特性,对高信噪比的短路电流可直接采用LMD提取基波电流和直流分量。图6为信号含30 dB噪声和不含噪声时的极值点分布图、平滑前后的局部均值函数和包络估计函数(跨度为7)。由图6(a)可知加入30 dB噪声后,信号极值点位置略有改变,由此而产生的平滑前的包络估计函数和局部均值函数有较大差异,如图6(b)所示;对比图6(b)、(c)可知经过1次平滑后二者的局部均值和包络估计函数比较接近。
图7为对含30 dB噪声的信号,采用LMD和HHT提取的基波电流和直流分量,2种方法获取的基波电流和直流分量很相似。但在分解过程中发现,应用HHT在分解含噪信号(30 dB)的过程中容易发生模态混叠(如图8所示)。其原因主要是当极值点含有噪声时,HHT的分解结果会受到影响;LMD获取包络时采取了滑动平均算法,由于其具有平滑滤波功能,在处理含30 dB噪声的短路电流时不存在这一问题。
2.2.2 低信噪比(15 dB)时基波和直流电流的提取
大量仿真发现,当信噪比降低时,求取信号极值时会出现伪极值点,此时直接采用LMD也会出现模态混叠问题。为解决这一问题,本文提出了基于前置滑动平均的LMD算法提取突然短路电流的基波和直流分量,即在求取信号极值点之前,运用有权重的中心滑动平均算法对其进行滤噪处理,然后再对降噪后的信号应用LMD提取直流分量和基波电流。

图6 信号含30 dB噪声和不含噪声时的极值点以及一次平滑前后a11和m11的对比图Fig.6 Comparison of extreme point,unsmoothed and smoothed a11/m11between signal with 30 dB noise and noiseless signal

图7 HHT和LMD提取的基波和直流分量Fig.7 Fundamental and DC components extracted by HHT and LMD
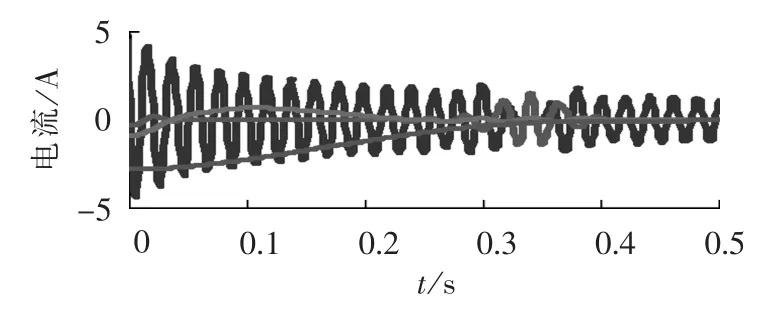
图8 HHT处理短路电流时发生的模态混叠问题Fig.8 Modal aliasing during short circuit current processing by HHT
图9为信号信噪比为15 dB时,运用前置滑动平均算法获取的直流分量和基波电流。由图9(a)可知,平滑滤波器较好地滤除了短路电流的噪声成分,特别是在极值点处的毛刺被有效滤除;图9(b)为短路电流的LMD结果,相对于没有噪声的分解结果,虽多了1个PF分量,但没有发生模态混叠问题;仔细观察,可将PF1作为基波电流,PF2和残差信号相加可得直流电流,图9(c)、(d)为理论上的基波电流、直流电流和实际提取的基波电流、直流电流的对比图,从中可知本文所提方法可在低信噪比(15 dB)条件下有效提取短路电流中的基波电流和直流分量。
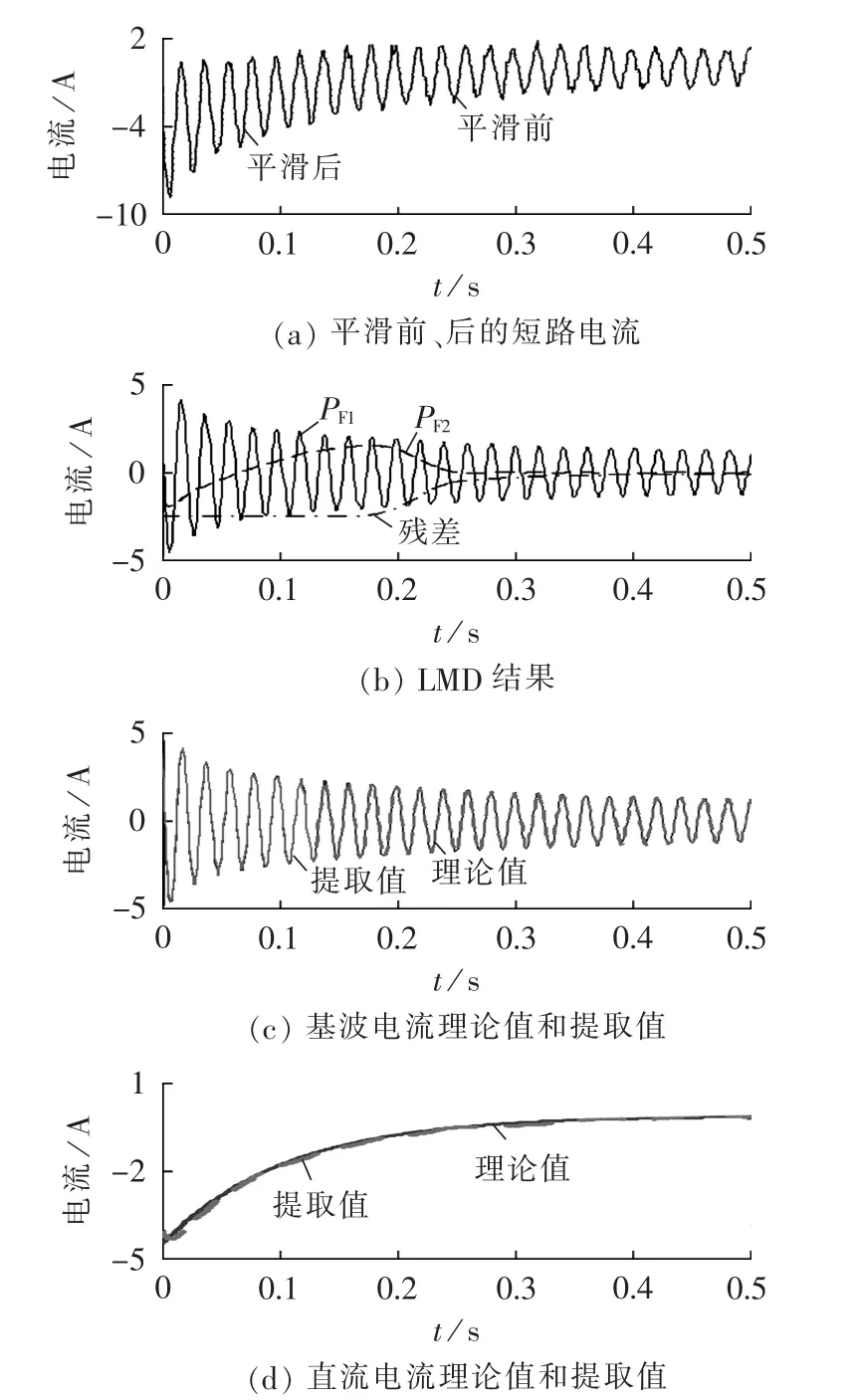
图9 低信噪比(15 dB)信号的分析结果Fig.9 Analytic results of signal with low SNR(15 dB)
2.2.3 连续高频噪声时直流和基波分量的提取结果
采用普通数据采集卡采集的同步电机突然短路电流信号如图10所示,采用LMD的结果如图11所示。仔细观察图11可知,PF1和PF2是高频、低能量的噪声信号;PF3可认为是基波电流分量;将PF4、PF5和残差信号相加可得直流电流分量。采用LMD提取的直流电流分量和基波电流分量如图12所示。
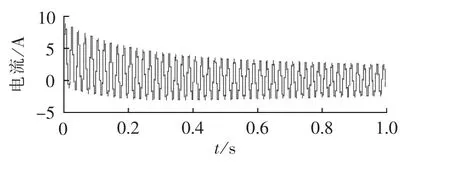
图10 测试电流信号Fig.10 Test current waveform

图11 基于LMD的测试电流分解结果Fig.11 Results of test current decomposition based on LMD

图12 运用LMD提取的直流电流分量和基波电流分量Fig.12 Fundamental and DC components extracted by LMD
3 不同噪声水平下参数辨识结果
为验证本文所提方法的正确性,运用LMD分别对第2节中的理想的短路电流、高信噪比(30 dB)短路电流、低信噪比(15 dB)的突然短路电流进行分析,从中提取直流电流分量和基波电流分量。以相对均方误差为目标,与EMD方法作比较。不同噪声情况下,2种方法获取的直流电流分量i0、基波电流分量i1、基波包络a1的相对均方误差如表1所示。从表1中可知,与LMD方法对应的相对均方误差明显小于EMD方法,特别是低信噪比时,EMD方法对应的均方误差明显增大,其原因为:EMD采用三次样条插值拟合包络函数容易引起过包络、欠包络现象;LMD采用滑动平均算法拟合包络函数,而滑动平均算法有滤波器功能,相对于EMD的三次样条插值拟合包络方法,LMD的端点效应较小;另外,LMD获取1个PF分量是采用除法,与EMD获取1个IMF分量采用减法相比,“筛分”次数较少,而“筛分”次数越少,端点效应对数据的污染程度也就越轻,分解的效果也就越好。

表1 2种方法的相对均方误差Table 1 Relative mean square errors of two methods
对直流电流分量和基波电流分量分别采用稳健回归最小二乘[14]和 Prony 算法[3-4]进行辨识(限于篇幅,详细过程请参阅文献[3-4,14]),参数辨识结果以及相对误差如表2—4所示。
由表2—4可知,对于理想信号,LMD和EMD方法对应的参数辨识效果都具有较高的辨识精度,但LMD方法获取的参数辨识精度略好于EMD方法;当突然短路电流含有较少的随机噪声信号(如信噪比为30 dB),LMD方法对应的参数辨识精度有不同程度的下降,但LMD辨识出的大部分参数的相对误差小于1%;随噪声含量加大(如15 dB),LMD方法对应的参数辨识精度会进一步下降,但大多数参数的相对误差小于2%,属于可接受的范围。而随着噪声成分的增多,EMD方法对应的参数辨识效果较差,相对误差较大,甚至超过6%。
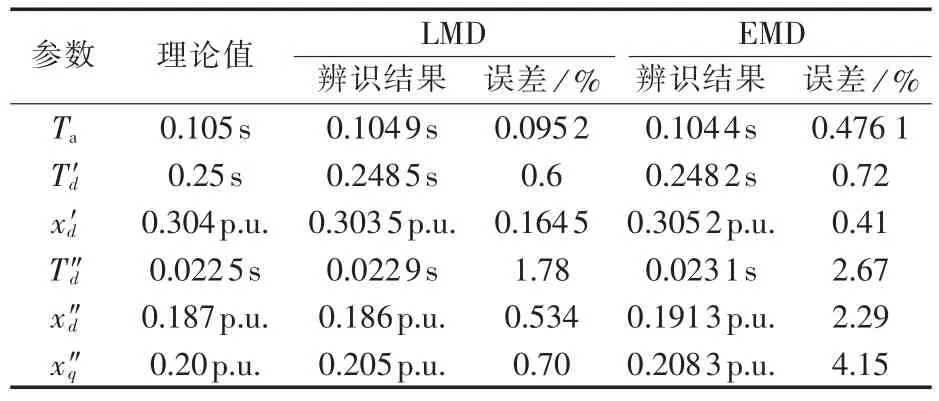
表3 信噪比30 dB时基于LMD和EMD的参数辨识结果Table 3 Results of parameter identification based on LMD and EMD for signal with high SNR(30 dB)
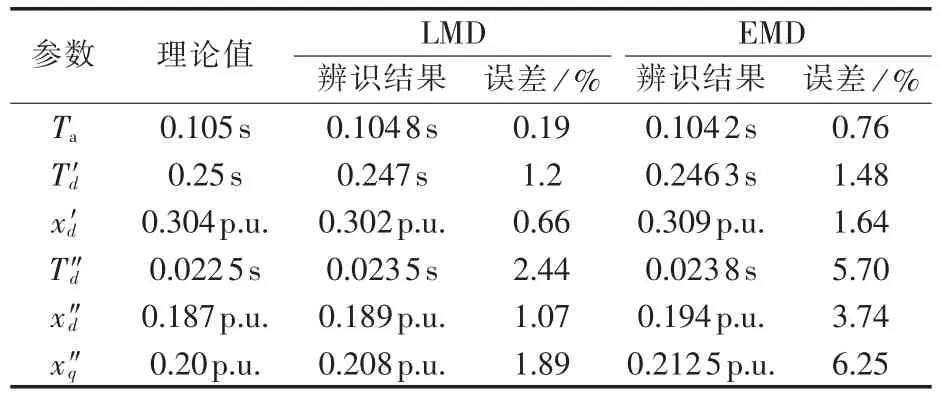
表4 信噪比15 dB时基于LMD和EMD的参数辨识结果Table 4 Results of parameter identification based on LMD and EMD for signal with low SNR(15 dB)
4 实验案例
为进一步验证所提方法的可行性和有效性,对图12中的直流电流分量和基波电流分量分别进行参数辨识,然后将参数辨识结果代入式(9),获取辨识的同步发电机突然短路电流信号并与实测的突然短路电流波形(滤除高频噪声)对比。
对实测的同步发电机突然短路电流的辨识结果为:Ta=0.1587s,Td′=1.644 7 s,Td″=0.336 7 s;xd′=0.2117 p.u.,xd″=0.1482 p.u.,xq″=0.2189 p.u.。
由辨识的参数通过式(9)获取的电流和实测的电流(滤除高频分量)对比波形如图13所示。
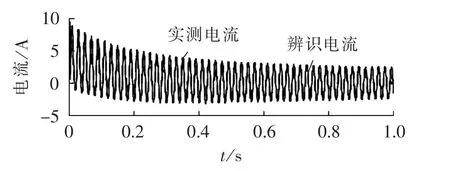
图13 实测电流波形和辨识电流波形Fig.13 Measured current waveform and identified current waveform
比较图中辨识电流波形和实测波形(已滤除高次谐波和噪声)可知,两者取得了较好的吻合,二者的相对均方误差为2.25%,验证了本文所提方法的可行性。试验中,采用EMD方法获取的辨识电流和试验电流的相对均方误差为2.83%,由此可知本文所提方法的有效性和优越性。
5 结论
本文首次将LMD应用于同步电机参数辨识领域,提出了基于LMD的同步电机参数辨识新方法,所得主要结论如下。
a.在处理同步电机突然短路电流时,合适的滑动平均跨度为7。
b.LMD可将高信噪比的突然短路电流信号分解为直流电流和基波电流2个分量;较之EMD方法,LMD的分解结果更为简单、准确,不存在模态混叠问题。
c.低信噪比时,前置滑动平均的LMD方法可有效提取直流电流和基波电流分量。
d.较之EMD方法,基于LMD的参数辨识结果受噪声影响较小,参数辨识精度较高。
