双馈风电机组次同步振荡阻尼特性与抑制策略
2015-09-21高本锋杨大业宋瑞华赵书强张学伟
高本锋,李 忍,杨大业,宋瑞华,赵书强,刘 晋,张学伟
(1.华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003;2.中国电力科学研究院,北京 100192;3.国网北京经济技术研究院,北京 102209)
0 引言
我国风能具有地域性分布的特点,一般都远离负荷中心,因此,大规模、远距离风电外送必不可少[1-3]。串联电容补偿是目前风电并网远距离送出的主要输电措施[4-9]。
与火电机组类似,风电机组经串补送出时也面临次同步振荡 SSO(Sub-Synchronous Oscillation)的威胁。按照相互作用的对象不同,风电机组的SSO问题主要包括:风电机组轴系与串补之间的相互作用而引发的次同步谐振SSR(Sub-Synchronous Resonance)、风电机组控制器与风电机组轴系相互作用而引发的次同步振荡SSTI(Sub-Synchronous Torsional Interaction)、风电机组控制器与串补之间的相互作用引发的次同步控制相互作用SSCI(Sub-Synchronous Control Interaction)。研究结果表明,风电机组的SSR和SSTI问题并不严重,发生概率较大和危害严重的是SSCI[9]。
SSCI是近年来出现的一种新的次同步振荡现象。2009年9月,在美国德克萨斯州南部的风电场,因断线引起的风电场直接经串补线路送出造成了风电机组端口电压和输出电流在次同步频率下的快速发散型振荡,大量机组跳机,撬棒电路损坏[10-11]。这是目前公布的第一起SSCI事故。分析结果表明,这是由双馈风电机组DFIG(Doubly-Fed Induction Generator)转子侧换流器与固定串补电容相互作用引起的[10-15]。与SSR和SSTI不同,SSCI由于与风电机组的轴系扭振频率无关,振荡频率完全取决于转子侧换流器控制以及电气输电系统的结构,因此不存在固定的振荡频率[12-15];此外,由于与机械系统无关,系统对振荡的机械阻尼较小,其电压和电流的振荡发散速度远快于SSR和SSTI,由此导致的危害更为严重。
目前国内外针对SSCI的发生机理、阻尼特性以及抑制措施等方面进行了初步研究。文献[13-14]通过时域仿真法分析SSCI发生的原因,但都缺乏机理层面的有力证明。文献[16]采用特征值分析法,分析了风速、串补度和控制器参数对SSCI阻尼特性的影响,但DFIG采用的是准稳态模型,只能保证在基波频率下的准确性,其在次同步频率范围内的精度有待商榷。而基于时域仿真实现的复转矩系数法采用的是电磁暂态模型,充分考虑了非线性因素的影响,弥补了特征值分析法的不足,保证了分析结果的准确性[17-18]。 文献[12]为 DFIG 设计了 SSCI阻尼控制器,通过在有功控制部分附加一个次同步阻尼控制器SSDC(Sub-Synchronous Damping Controller)来抑制SSCI,但该文献没有给出参数整定方法,其抑制效果还有待验证。
本文首先介绍风电并网系统总体模型,然后简述DFIG工作原理以及本文所采用的转子侧换流器RSC(Rotor Side Converter)的控制策略,最后重点分析DFIG中换流器的工作原理及输出特性,建立基于交流受控电压源和直流受控电流源的等效仿真模型。基于PSCAD/EMTDC仿真平台下的DFIG等效模型,采用时域仿真实现的复转矩系数法——测试信号法,揭示风速、转子侧换流器的控制参数、输电线路串补度及线路电阻对风电并网系统电气阻尼的影响。为提高DFIG的电气阻尼,提出在DFIG转子侧换流器控制模块中附加混合次同步阻尼控制器H-SSDC(Hybrid Sub-Synchronous Damping Controller)以抑制SSCI的方法,并对其有效性进行验证。
1 系统建模
1.1 风电并网系统
DFIG经固定串补接入无穷大系统的示意图如图1所示。DFIG表示100台1.5 MW的机组聚合而成的风电场,参数聚合方法参见文献[19],风电场聚合后参数如表1所示。感应发电机采用单刚体模型,不考虑扭振相互作用的影响,感应发电机、变压器和无穷大电源参数按照文献[20]设置。表1中感应发电机的阻抗参数均以自身额定功率和电压为基准值。
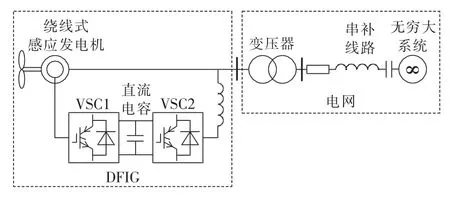
图1 DFIG经串补并网结构示意图Fig.1 Schematic diagram of DFIG integrated to power system through transmission line with series compensation
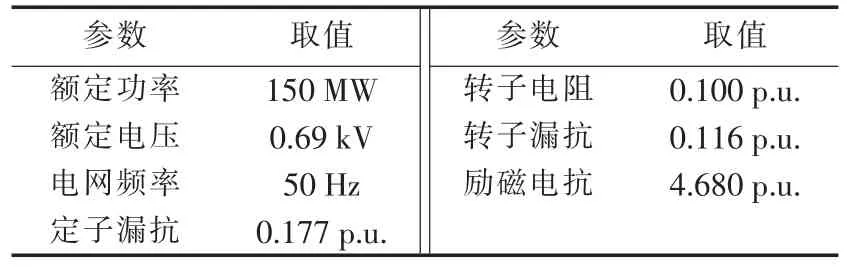
表1 风电场聚合后参数Table 1 Parameters of aggregated wind farm
电网模型中,加入串补电容后,系统的串补度(XC/Xl)为 20%,XC为串补电容容抗,Xl包含输电线路电抗、发电机定子漏抗、变压器漏抗和无穷大电源电抗。DFIG模型是系统建模的关键点,后文将详细介绍。
1.2 DFIG工作原理
DFIG结构如图1所示,除定子绕组与电网有电气连接外,转子侧通过一个交-直-交换流器(简称换流器)与电网相连。换流器在转子绕组中施加变频电流,其频率根据转速动态调节,从而在定子绕组中感应出恒频电势,以实现变速恒频运行。换流器一般包括转子侧换流器、直流电容及电网侧换流器GSC(Grid Side Converter),转子侧换流器和电网侧换流器均为电压源换流器VSC(Voltage Source Converter),分别对应图中 VSC1、VSC2。VSC使用全控器件IGBT,通过脉宽调制调节VSC出口电压,间接控制转子励磁电流以及网侧电流,最终实现对DFIG输出功率和电压等关键运行参数的控制[18]。
图2为DFIG转子侧换流器控制系统框图。采用dq解耦的双闭环控制,外环为有功、无功功率控制,内环为电流控制[20-21]。d轴采用定无功功率Qref控制,q轴根据最大风能追踪原理求取在某一风速下风力机输出的最大功率,减去机械损耗后,将其作为DFIG输出有功功率的参考值 Pref。 Δps、Δqs分别为DFIG输出的瞬时有功及无功功率变化量;p为微分算子;Rr为转子电阻;Lm为励磁电感;Ls为定子电感;Lr为转子电感;ird、irq、urd、urq分别为转子电流、转子电压 d、q 轴分量;ωs、ωr分别为定、转子磁场的旋转角速度;a1=Lm/Ls,a2=Lr-L2m/Ls;ψ1为定子磁链;kg2、ki2、kg1、ki1分别为控制器的内、外环 PI参数。 这些参数对于双馈风电机组的安全稳定运行具有重要意义,将会在后文研究SSCI特性中着重介绍。
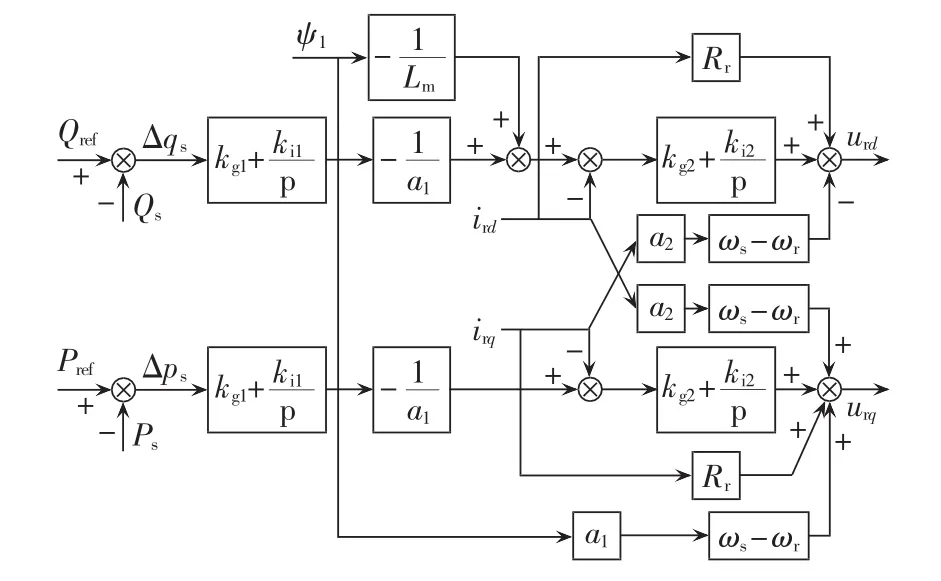
图2 DFIG转子侧换流器控制框图Fig.2 Block diagram of DFIG rotor side converter control
2 换流器的等效模型
2.1 等效原理
VSC采用正弦脉宽调制SPWM(Sinusoidal Pulse Width Modulation)控制IGBT的通断,使换流桥出口处产生幅值为±Ud/2的电压脉冲序列,其中Ud为换流器直流侧电压。如果调制信号波为Msin(2πfrt-δ)(M 和 δ分别为调制比和移相角度),则换流器出口电压脉冲序列中对应频率fr的电压分量 uc如式(1)所示:
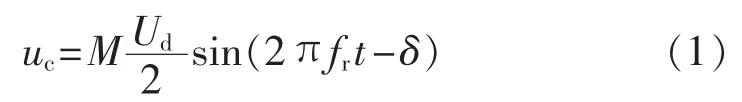
由式(1)可以看出,通过控制SPWM的调制比和移相角度,VSC具有幅值和相位均可控的受控电压源特性;另一方面,将换流桥的损耗等效并入换流变压器的电阻后,由换流桥交直流两侧的有功平衡关系可得:

其中,icx、ucx分别为VSC交流侧三相电流和电压;Pc为转子注入到直流侧的有功功率;id为直流侧电流。
由式(2)可以看出,对于直流侧电容部分,其电流大小由Pc和Ud决定,因此具有受控电流源的特性。
基于VSC具有的受控电压源特性以及直流电容具有的受控电流源特性[22],本文建立了受控源等效换流器模型,将DFIG转子侧换流器、网侧换流器以及换流器直流部分采用受控源予以等效,如图3所示。该模型避免了开关器件所产生的高次谐波对DFIG电气阻尼计算结果的影响,在本文研究的次同步频率范围内,能够得到光滑且连续的电气阻尼特性曲线。
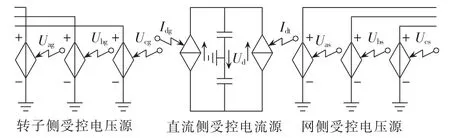
图3 受控源等效换流器模型Fig.3 Equivalent model of converter with controlled sources
2.2 模型验证
在PSCAD/EMTDC下建立如图1所示风电经串补并网系统。根据DFIG换流器建模方法的不同,本文建立了2个模型:换流器采用开关器件建模的DFIG模型,记为开关模型;使用受控源对换流器进行替换的DFIG模型,记为等效模型。
待等效模型运行稳定后,改变输入信号设定值,使控制信号阶跃变化:10 s时风电机组输出无功从0.04 Mvar阶跃至0.44 Mvar;12 s时风电机组输出有功从0.66 MW阶跃至0.96 MW。等效模型的阶跃响应特性如图4所示。
由图4可知,输入信号设定值阶跃变化时,等效模型能够快速、准确地跟踪设定值。同时,当风电机组输出无功设定值改变时,有功输出基本不随之变化;当风电机组输出有功设定值改变时,无功输出也基本保持不变。因此,将换流器用受控源等效后,等效模型不仅能够快速、准确地跟踪系统指令,而且仍能实现有功无功输出解耦控制。
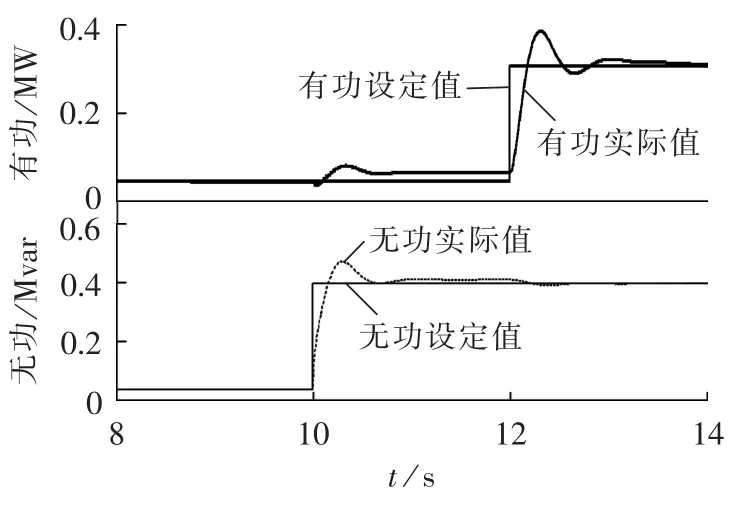
图4 等效模型控制系统阶跃响应Fig.4 Step response of control system for equivalent model
2.3 2种模型暂态响应对比
将开关模型和等效模型设置成相同的参数,对比2个模型在相同故障下的暂态响应。图5、6分别给出10 s时发生a相接地故障和三相短路故障情况下,风电机组功率输出和a相电流。故障点为串补线路末端,持续时间0.05 s。
由仿真结果可以看出,上述2种故障情况下,等效模型和开关模型的暂态响应基本一致,具有相同的暂态特性。
2种模型的仿真效率如表2所示,在相同的仿真步长下,等效模型的仿真用时较开关模型大为缩短,仿真计算效率显著提高。将等效模型的这一特点运用于DFIG的仿真计算中,对于解决多机系统电磁仿真耗时过长这一工程难题,具有重要参考意义。
3 DFIG的次同步振荡阻尼特性
3.1 分析方法
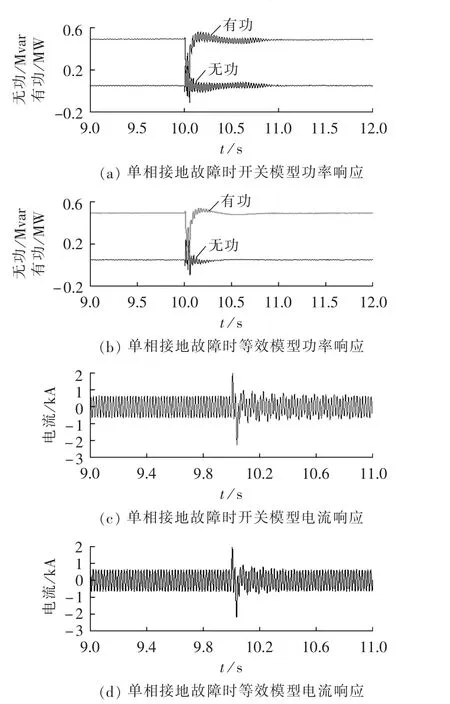
图5 a相接地故障时开关模型和等效模型暂态响应Fig.5 Transient response of switch model and equivalent model to grounding fault of phase a
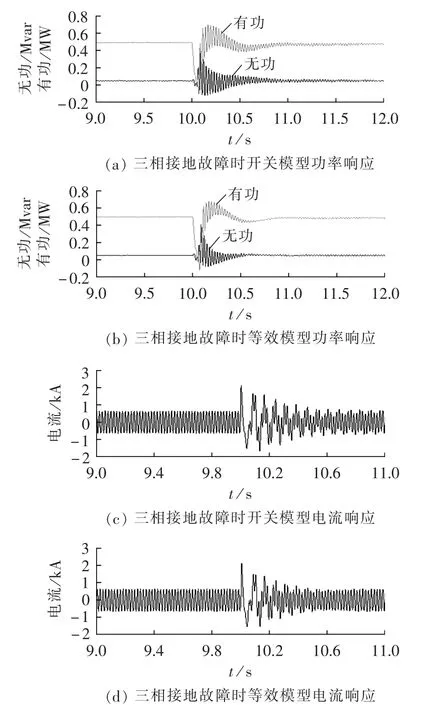
图6 三相接地故障时开关模型和等效模型暂态响应Fig.6 Transient response of switch model and equivalent model to three-phase grounding fault
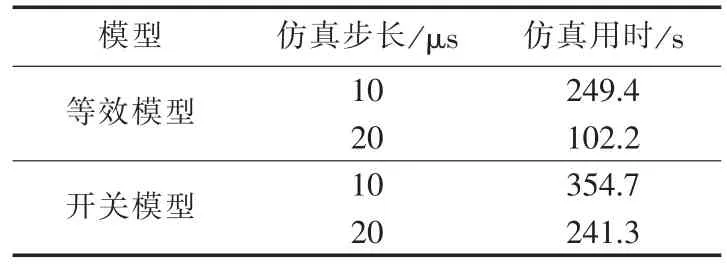
表2 2种模型的仿真用时对比Table 2 Comparison of simulation time between two models
复转矩系数法是I.M.Canay提出的一种分析次同步振荡的基本方法[17-18]。在小扰动下,待研究的发电机对于系统中频率为λ的振荡分量,电磁转矩增量可以表示为:
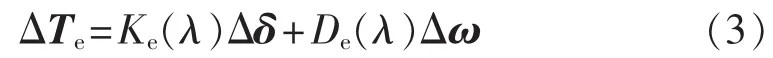
其中,KeΔδ为同步转矩,DeΔω 为阻尼转矩,Ke、De分别为同步转矩系数和阻尼转矩系数,Δδ、Δω分别为相对同步旋转坐标系的功角增量和角速度增量。由式(3)得:
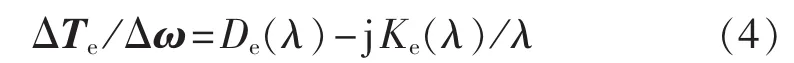
阻尼转矩系数为:
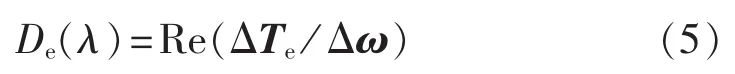
测试信号法又称为基于时域仿真的复转矩系数法,当系统稳定运行后,在发电机转子施加一系列小扰动振荡转矩ΔTm,所加ΔTm的要求是不能破坏系统线性化条件。然后对系统进行仿真,提取出同周期内的数据量ΔTm和Δωm,计算得出相关的振荡特征信息。其中,计算电气阻尼系数的步骤如下。
①在待研究的运行工况下,在转子上施加一串次同步频率为f的小幅扰动转矩ΔTm:
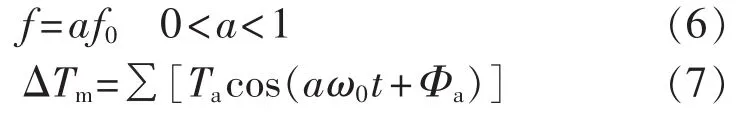
其中,f0为工频 50 Hz;ω0=2πf0;Φa为 ΔTm相位;Ta为ΔTm幅值。
②当系统再次进入稳态后,截取一个公共周期上的发电机电磁转矩Te和发电机转速ω。
③将上述2个量进行频谱分解,得到不同频率对应的ΔTe和Δω,由式(5)计算得到电气阻尼转矩系数(简称电气阻尼)。
3.2 SSCI的机理
当串补线路中出现谐振频率为ωn的电流扰动时,DFIG输出的a相电流可以表示为:
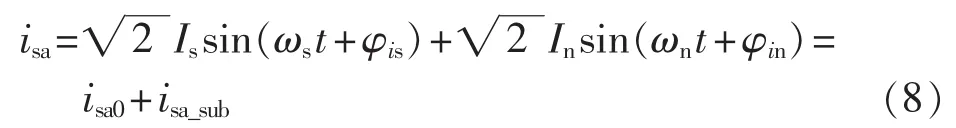
其中,Is、φis分别为基波电流isa0的有效值和初相位;In、ωn、φin分别为次同步电流 isa_sub的有效值、角频率和初相位。
dq坐标系下,次同步电流分量可以表示为:
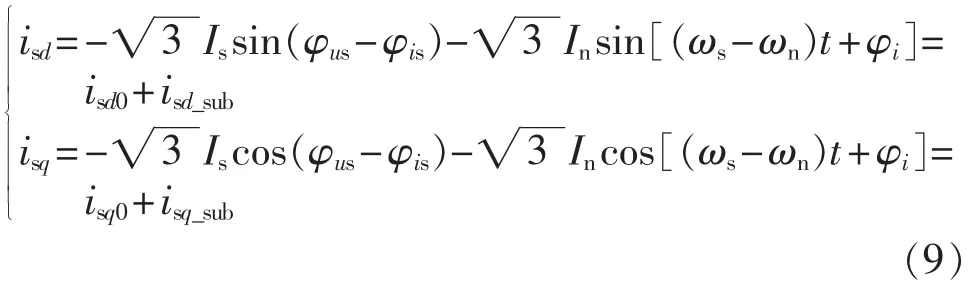
其中,φi=φus-φin;isd0、isq0分别为 d、q 轴定子电流的直流分量;isd_sub、isq_sub分别为 d、q轴定子电流的次同步分量。
另一方面,定子侧的三相次同步电流分量形成的旋转磁场切割转子绕组,在转子绕组中感应出角频率为ωr-ωn的三相次同步电流,其d、q轴分量为:
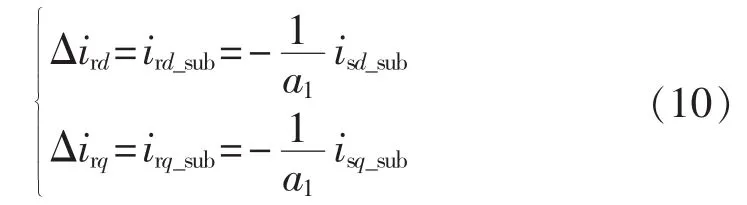
系统扰动引起的转子侧变流器输出电压的次同步分量为:
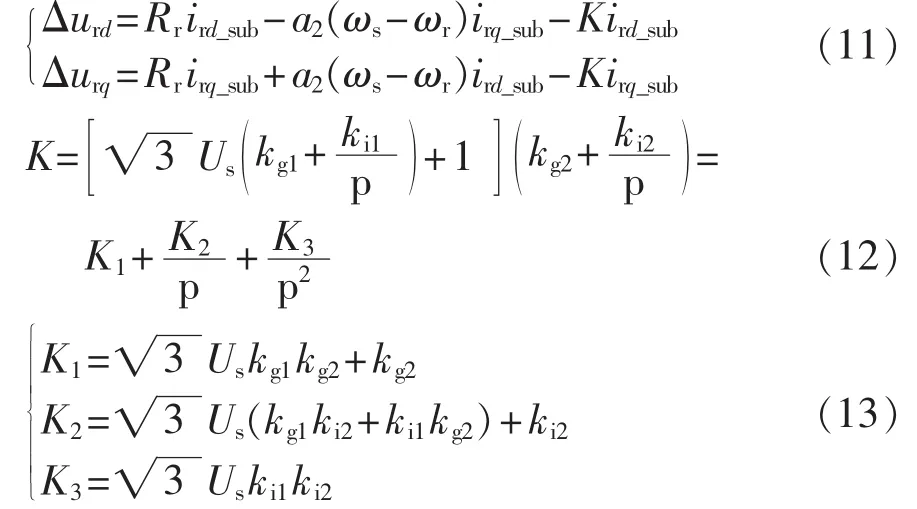
这部分扰动量反作用于转子绕组,在转子上施加角频率为ωs-ωn的次同步电压d、q轴分量,产生新的次同步电流,其感应到定子侧的次同步电流d、q轴分量为:
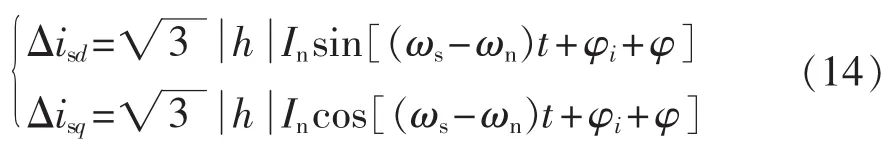
其中,φ、h分别为dq坐标系下转子侧变流器输出电压扰动量感应到定子绕组的次同步电流与原始扰动电流的相位偏差和幅值增益,计算方法如式(15)—(17)所示。
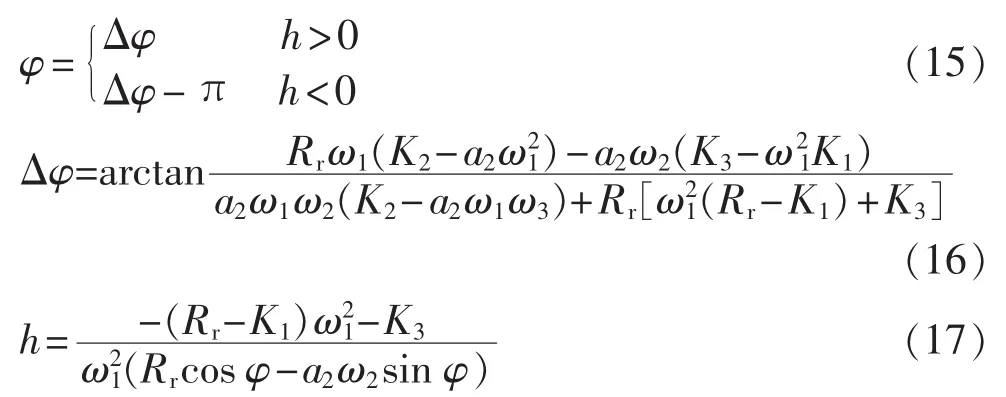
其中,ω1=ωs-ωn;ω2=ωr-ωn;ω3=ωs-ωr。
定子a相新的次同步电流分量为:
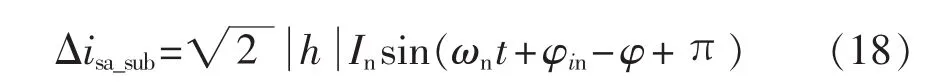
3.3 SSCI的特性分析
目前,国内外研究认为SSCI主要受到风速、转子侧换流器参数、串补度和线路电阻的影响[12,23-29]。本文计算待研究系统在次同步频率下的电气阻尼,以系统机械阻尼与电气阻尼之和为负值,则可能发生SSCI为理论依据,通过分析次同步频率下的电气阻尼大小,探究系统参数对SSCI的影响。感应发电机的参数按照表1设定,转子侧换流器的PI参数按表3所示取值,初始风速为10 m/s,初始串补度为20%。采用控制变量的研究方法,每次仅改变一个参数,其余参数采用初始值。
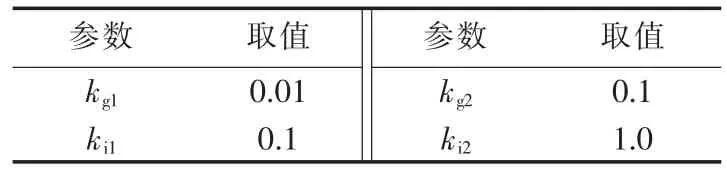
表3 转子侧换流器的PI参数Table 3 PI parameters of rotor side converter
3.3.1 风速对SSCI的影响
当风速为 9 m/s、10 m/s、11 m/s 时,计算得到系统的电气阻尼De随频率变化的曲线如图7所示。随着风速的增加,电气阻尼最低点逐渐上移,电气阻尼逐渐增加,系统发生SSCI的概率逐渐减小。
3.3.2 转子侧换流器PI参数对SSCI的影响
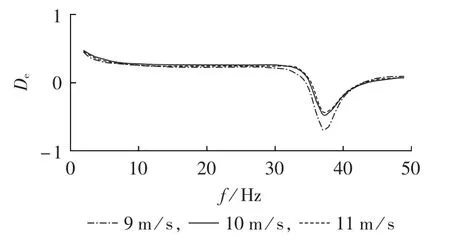
图7 系统在不同风速下的电气阻尼系数Fig.7 Electrical damping coefficient of system for different wind speeds
设定换流器内环比例增益kg2分别为0.05、0.1和0.2,计算得到系统的电气阻尼随频率变化的曲线如图8所示。随着换流器内环比例增益kg2的增大,电气阻尼最低点的频率逐渐增大,即系统发生SSCI的频率逐渐增大,且系统电气负阻尼绝对值逐渐增大,发生SSCI的概率也将逐渐增大。
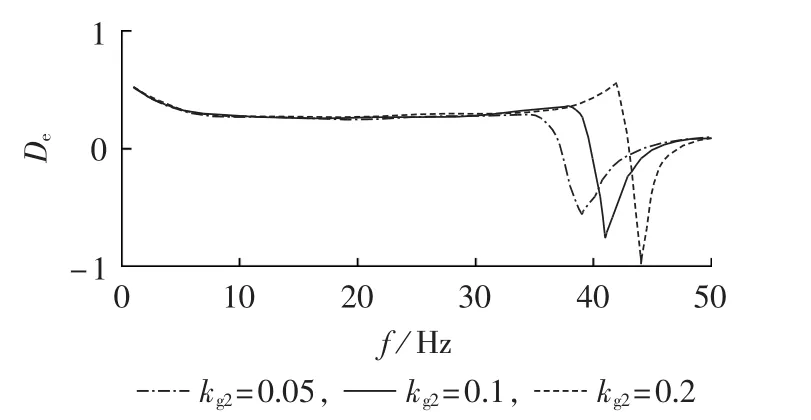
图8 系统在不同内环比例增益下的电气阻尼系数Fig.8 Electrical damping coefficient of system for different inner-loop gains
当设定换流器内环积分时间常数Tri=kg2/ki2分别为0.06、0.08和0.1时,计算得到系统的电气阻尼随频率变化的曲线如图9所示。随着换流器内环积分时间常数Tri的减小,电气阻尼最低点的频率不变,即系统发生SSCI的频率不变,然而系统电气负阻尼绝对值逐渐增大,因此发生SSCI的可能性逐渐增加。
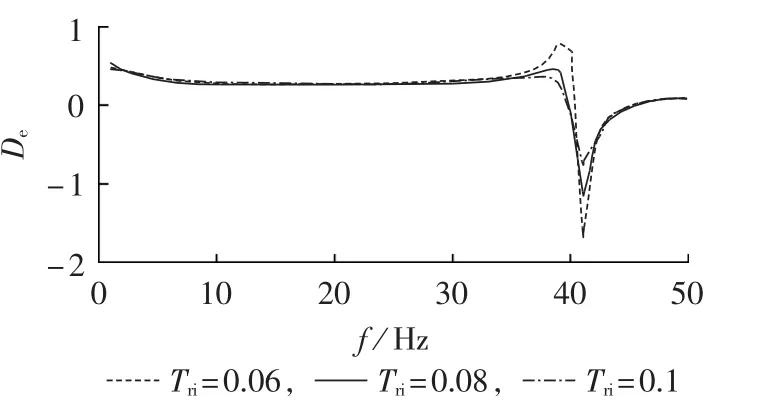
图9 系统在不同内环积分时间常数下的电气阻尼系数Fig.9 Electrical damping coefficient of system for different inner-loop integral time-constants
当设定换流器外环比例增益kg1分别为0.01、0.5和1时,分别计算De随频率变化的曲线如图10所示。可以看出,随着换流器外环比例增益kg1的增大,电气阻尼曲线基本不变,即kg1对SSCI影响不大。
同理,当设定换流器外环积分时间常数Trd=Trq=kg1/ki1分别为0.01、0.5和1时,分别计算系统的电气阻尼随频率变化的曲线如图11所示。随着换流器外环积分时间常数Trq的增大,电气阻尼曲线基本不变。因此,SSCI对换流器外环比例增益和积分时间常数均不敏感。
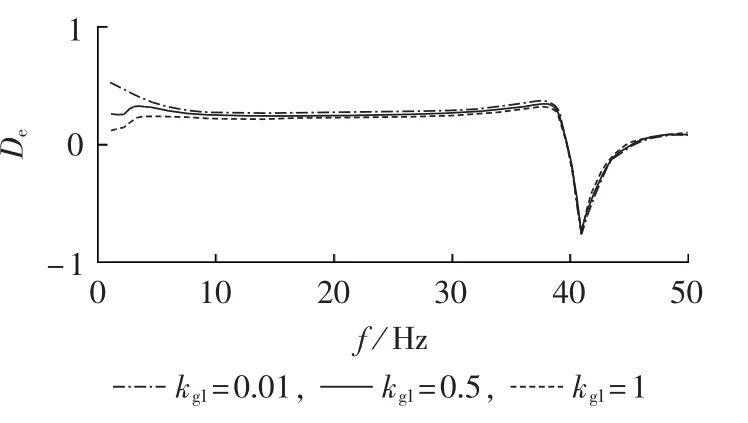
图10 系统在不同外环比例增益下的电气阻尼系数Fig.10 Electrical damping coefficient of system for different outer-loop gains
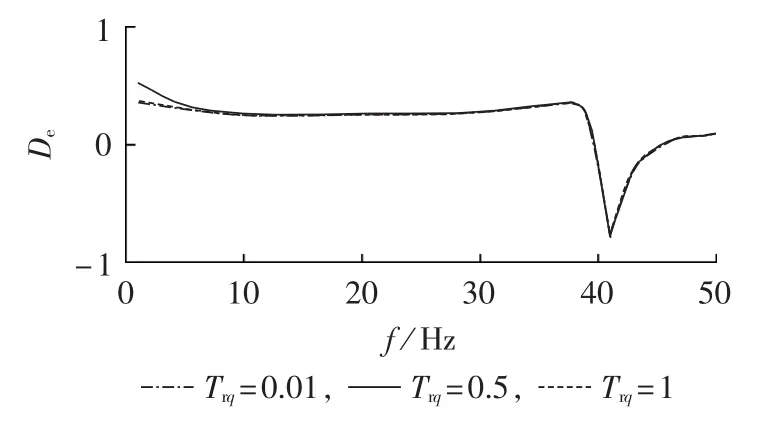
图11 系统在不同外环积分时间常数下的电气阻尼系数Fig.11 Electrical damping coefficient of system for different outer-loop integral time-constant
3.3.3 串补度对SSCI的影响
研究表明,SSCI是由转子侧换流器与固定串补间的相互作用引起的[10-15]。因此,线路串补度作为固定串补最重要的参数,值得深入研究。当设置线路串补度(XC/Xl)为20%和40%时,分别对系统进行电气阻尼计算。计算得到系统的电气阻尼随频率变化的曲线如图12所示。
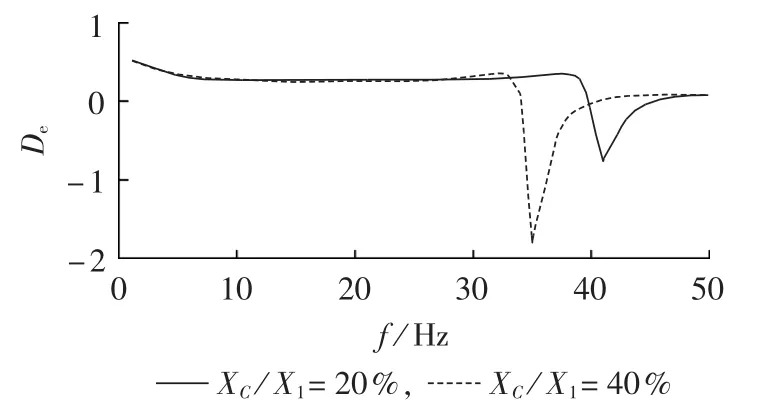
图12 系统在不同串补度下的电气阻尼系数Fig.12 Electrical damping coefficient of system for different series compensation degrees
由图12得,随着系统线路串补度的增大,电气负阻尼绝对值逐渐增大;电气负阻尼最低点向左移,发生SSCI的频率逐渐减小。因此串补度不仅影响系统电气阻尼的大小,而且影响振荡频率。
同时,由串补度的分析结果可知,当输电线路电抗发生改变时,若此时串补电容不变,线路电抗的变化将使系统串补度发生改变,系统的电气阻尼以及振荡频率也会相应发生变化。因此,线路电抗也会影响系统电气阻尼以及振荡频率,影响的结果本质上与串补度相同。
3.3.4 线路电阻对SSCI的影响
当线路电阻分别为14 Ω、15 Ω和16 Ω时,分别对系统进行电气阻尼计算。系统的电气阻尼随频率变化的曲线如图13所示,为便于观察,图中给出了电气阻尼最低点的局部放大图。
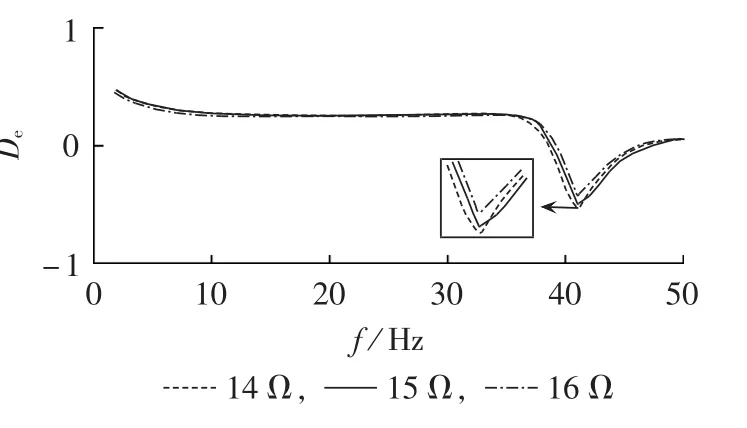
图13 系统在不同线路电阻下的电气阻尼系数Fig.13 Electrical damping coefficient of system for different transmission line resistances
由图13可知,随着系统线路电阻的增大,电气阻尼最低点的频率不变,即系统发生SSCI的频率不变,但电气负阻尼绝对值逐渐减小,SSCI发生的概率逐渐减小。因为线路电阻可以为输电线路提供电气正阻尼,所以,随着线路电阻的增大,系统对SSCI的抑制作用增强。
4 SSCI抑制策略
4.1 原理
优化DFIG的控制策略是抑制SSCI最经济可行的措施。本文提出了一种在转子侧换流器中附加混合次同步阻尼控制器(H-SSDC)以抑制SSCI的方法。该方法在转子侧换流器的有功、无功外环控制环节分别配置有功阻尼控制器(P-SSDC)和无功阻尼控制器(Q-SSDC)。通过同时对有功功率和无功功率的动态调节作用,增加DFIG所提供的电气阻尼,进而达到抑制SSCI的目的,附加H-SSDC后转子侧换流器控制框图如图14所示。
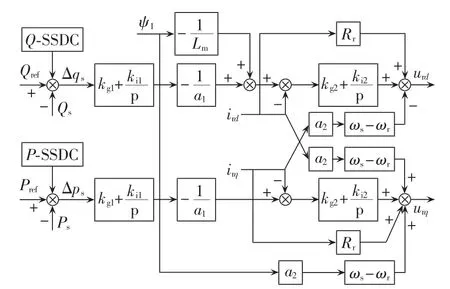
图14 配置H-SSDC后DFIG的转子侧换流器控制框图Fig.14 Block diagram of DFIG rotor side converter control with H-SSDC
下面以单机无穷大系统为例,分别介绍P-SSDC、Q-SSDC对于提高系统电气阻尼的理论依据,首先考虑有功阻尼控制环节的单独作用。
图15为单机无穷大系统的接线示意图,U1、U2分别为母线1、2的电压,δ为U1、U2之间的相角差,则发电机注入系统的有功和无功功率分别为:
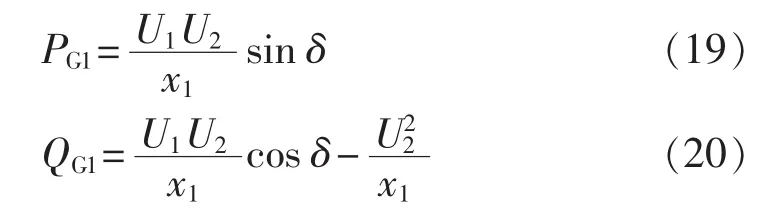
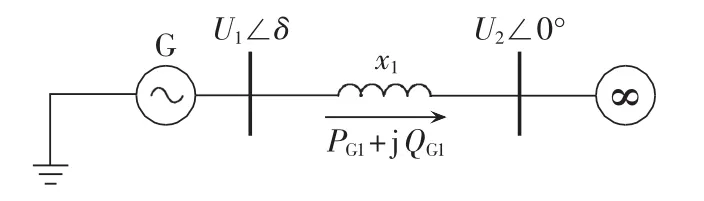
图15 单机无穷大系统接线图Fig.15 Schematic diagram of single-machine infinite-bus system
发电机G采用二阶经典模型且机械功率Pm恒定,则在标幺值系统下,G的运动方程为:
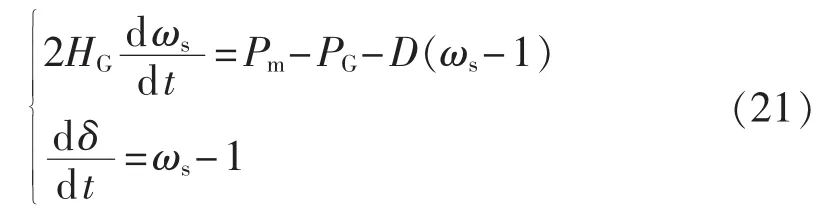
其中,HG为G的惯性时间常数;D为阻尼系数;ωs为G的定子磁场旋转角速度。对式(21)求小扰动量,则G的小扰动方程为:
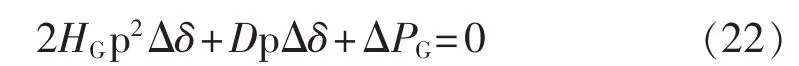
其中,ΔPG为G有功变量(不含P-SSDC调节部分)。假定P-SSDC仅引起G有功发生ΔPGΔ大小的改变,母线电压幅值U1、U2保持不变。设ΔPGΔ与G角速度的增量Δωs成正比,则有:
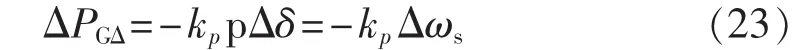
其中,kp为有功阻尼控制系数。由系统有功功率平衡可得:
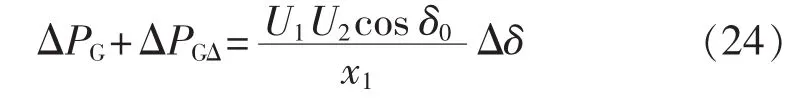
由式(24)可得 ΔPG,代入式(22)可得:
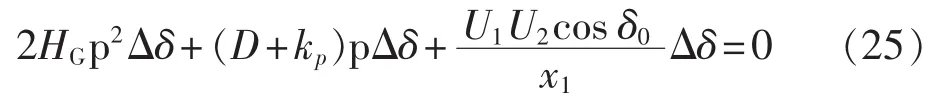
由式(25)可知,当kp>0时,系统阻尼系数增加,系统的阻尼特性得到改善。
下面分析附加Q-SSDC改善系统阻尼的原理,对电力系统无功控制装置的研究表明,动态调节注入系统的无功可进一步增加系统阻尼。
为简化分析,认为Q-SSDC仅引起G电压幅值的变化,变化量记为 ΔU1,分别对式(19)、(20)求小扰动量:
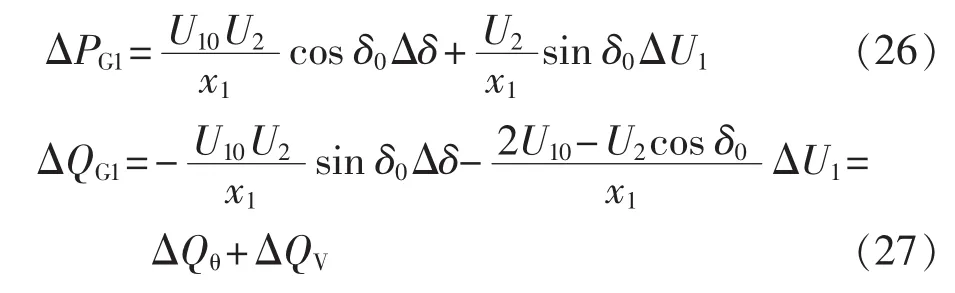
式(27)中包含了2部分,其中ΔQθ取决于功角δ的摆动;ΔQV取决于电压U1的波动,故Q-SSDC引起的无功增量ΔQGΔ即为ΔQV,且有:
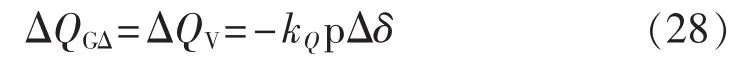
其中,kQ为无功阻尼控制系数。
由式(27)、(28)可得:
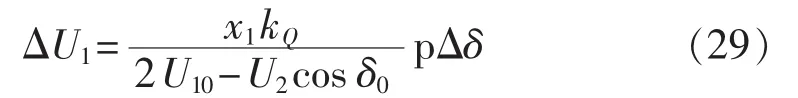
将式(29)代入式(26)、(22)可得加入 Q-SSDC 后G的小扰动方程如下:
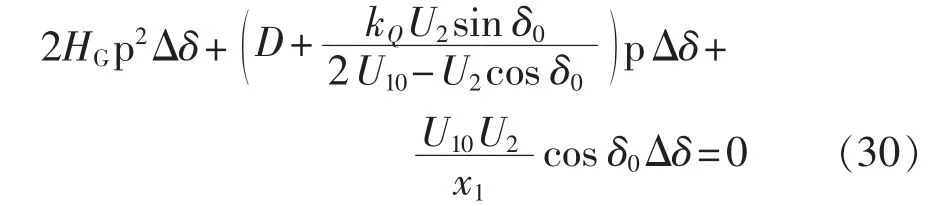
由式(30)可知,当kQ>0时,系统的阻尼系数增加,进而使系统的阻尼特性得到改善。因此,Q-SSDC通过调节机组无功输出,使机端电压发生变化,进而改变了系统中的有功功率,并最终产生阻尼系统振荡的力矩。
Q-SSDC和P-SSDC结构相同,如图16所示,以P-SSDC为例,包括输入信号、增益环节、移相环节以及限幅环节。输入信号为DFIG转速偏差Δω。移相环节采用 n 个移相函数(1+pTp1)/(1+pTp2)串联的形式。增益环节对阻尼控制器的输出进行调节,其大小与系统工况相关。
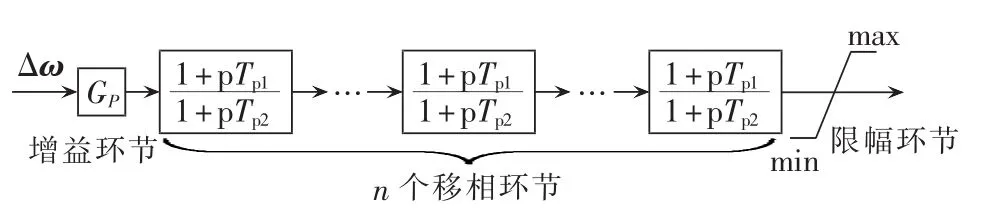
图16 P-SSDC结构图Fig.16 Structures of P-SSDC
4.2 参数整定
H-SSDC的移相环节以及增益环节的参数是影响其效果的关键。对移相环节和增益环节参数整定的目标为:从DFIG转子侧看过去,系统电气阻尼De=Re(ΔTe/Δω)最大。H-SSDC移相环节和增益环节整定步骤如下。
a.建立所分析系统的电磁暂态模型。
b.采用频率扫描法分别测量有功控制环节到ΔTe以及无功控制环节到ΔTe的相位差,分别记作θP和 θQ。
c.由式(31)分别计算P-SSDC和Q-SSDC的移相环节参数 T1、T2和 n。
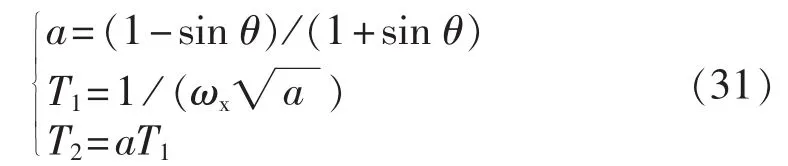
其中,ωx为振荡点角频率;θ为需要补偿的角度,通常 θ=θP/n(或 θQ/n),n 为移相环节个数;T1、T2为补偿环节时间常数。
d.基于电磁暂态模型,采用时域仿真法,确定增益GP和GQ,使其能够抑制各种扰动所引发的SSCI。
下面以P-SSDC参数整定为例,介绍具体的整定流程。根据复转矩系数法的分析结果,在电气负阻尼最大处(fe=41 Hz),ΔTe/Δω 的角度为 132°,采用 3个级联的补偿环节,每个环节补偿44°。由式(31)计算移相环节时间常数T1=0.01,T2=0.0018。最后,利用时域仿真确定使转子侧换流器稳定的增益GP=1。
4.3 验证
为验证H-SSDC抑制SSCI的有效性,利用本文建立的受控源等效换流器DFIG并网模型进行电气阻尼计算和时域仿真。文献[12]给出了在有功功率外环控制环节添加P-SSDC抑制SSCI的方法,并基于时域仿真进行了定性分析。因此,在验证H-SSDC的抑制效果时,与单独附加P-SSDC进行对比,采用电气阻尼计算和时域仿真2种方法对抑制效果进行较为全面的评价。
4.3.1 电气阻尼计算
设置串补度为30%,分别计算附加P-SSDC、HSSDC后,DFIG并网系统次同步频率下的电气阻尼,如图17所示。阻尼计算结果表明,H-SSDC由于在有功和无功外环控制环节均附加阻尼控制,引入的正阻尼比单独添加P-SSDC所引入的更大。
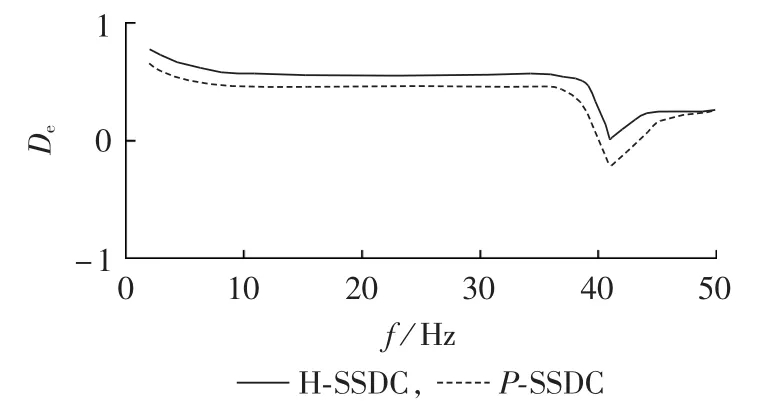
图17 附加P-SSDC与H-SSDC后电气阻尼系数Fig.17 Electrical damping coefficient of system with P-SSDC or H-SSDC
4.3.2 时域仿真
为进一步验证H-SSDC的有效性,在相同条件下进行时域仿真。设置串补度为30%,0.1 s投入串补电容。图18为无附加阻尼控制器与加入P-SSDC、HSSDC后DFIG输出功率变化情况(图中纵轴均为标幺值)。由仿真结果可知,投入串补电容后引起了SSCI,且振荡呈现发散的趋势;附加P-SSDC和H-SSDC均起到了抑制SSCI的效果;H-SSDC的抑制效果要比P-SSDC单独作用的效果更佳,这与电气阻尼的计算结果吻合。
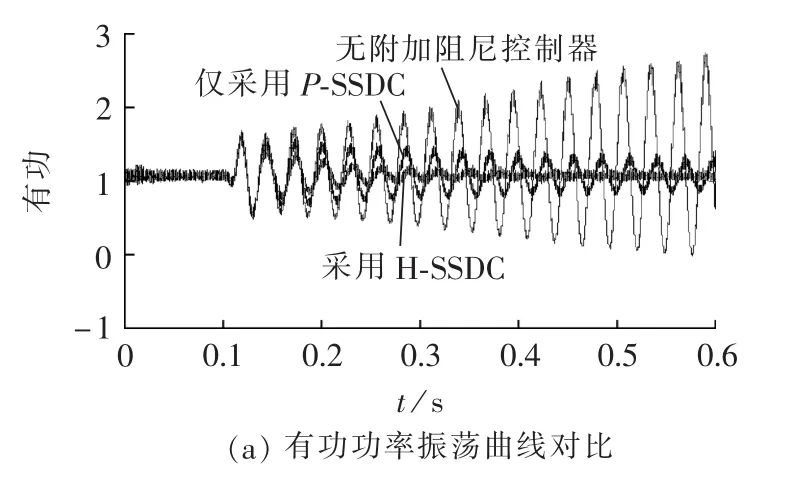
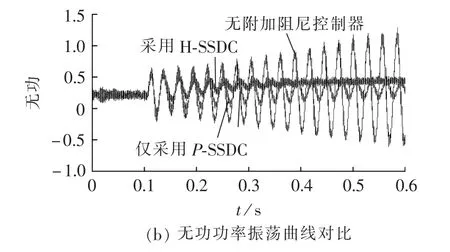
图18 加入SSDC前后DFIG输出功率Fig.18 Output power of DFIG with and without SSDC
5 结论
本文基于PSCAD/EMTDC仿真平台建立了受控源等效换流器DFIG并网模型,验证了等效模型的正确性,并揭示了其相对于开关模型仿真效率更高的优点。基于复转矩系数法分析了风速、转子侧换流器PI参数、线路串补度和线路电阻对DFIG阻尼特性的影响。分析结果表明,风速的减小、转子侧换流器PI参数内环增益的增大、积分时间常数的减小、串补度的增加以及线路电阻的减小均会助增DFIG电气负阻尼,增大SSCI发生的概率;外环PI参数对SSCI影响不大。设计了一种抑制SSCI的官H-SSDC,并给出了控制器参数的整定方法。电气阻尼计算和时域仿真结果均表明,H-SSDC可有效抑制SSCI,并且与现有单独添加P-SSDC的抑制措施相比,效果更显著。
