基于U-I曲线的单相自耦变GIC无功损耗算法

刘连光，秦晓培，2，葛小宁

（1.华北电力大学 新能源电力系统国家重点实验室，北京 102206；2.国网河北涉县供电公司，河北 涉县 056400）

0 引言

地磁暴在电网产生频率为0.0001～0.01 Hz的准直流的地磁感应电流GIC（Geomagnetically Induced Current）。GIC作用于电网变压器，会导致变压器直流偏磁饱和，衍生谐波、温升和无功波动等次生干扰[1-2]。一方面，由于太阳距地球的平均距离近1.5×108km，与地球直径相比非常远，太阳活动引发的地磁暴在全球的不同地区几乎同时发生，不同地区地磁暴的时间差不超过2 min，因此GIC及其衍生的次生干扰也具有全网同时性。另一方面，变压器的无功损耗与铁芯的材料、构成等很多因素有关。受这些因素以及电网规模大、变压器数量多的影响，准确计算电网GIC衍生的谐波、无功扰动等干扰非常困难。

实测数据表明[3]，与电网GIC衍生的变压器有功功率波动和谐波干扰相比，GIC衍生的无功扰动幅度大，还会引起电网的电压波动，而大量变压器的无功波动和全网的电压波动将会对电网的安全运行产生较大的影响[3]。在GIC引发的大量电网事故案例中，1989年加拿大魁北克大停电的起因是GIC引发的谐波及无功波动使输电线路和电网的静止无功补偿（SVC）装置跳闸，发生连锁反应和电网失去无功支撑，导致全网电压崩溃大停电[4]。随着我国长距离输电系统的建设，2000年以来，我国也发现了大量的GIC侵害电网的事件。其中，2004年11月10日广东岭澳核电站500 kV变电站实测的GIC的最大值为75.5 A[5]。 我国750 kV和1000 kV超/特高压电网分别采用六分裂和八分裂导线，输电线路的单位长度的直流电阻小，相同磁暴产生的GIC会更大[6]。评估变压器和电网的GIC无功扰动是GIC影响分析的基础。

国内外对变压器直流偏磁效应的研究主要集中在采用J-A理论等方法计算磁化特性，建立变压器的磁电路模型，从而实现变压器直流偏磁各种电磁干扰效应的理论计算[7-8]。J-A理论算法虽然具有较高的计算精度，但由于计算需要的各种制造参数为商业机密，不易获取，同时变压器的结构、类型复杂，磁电路模型迭代的计算量比较大，因此J-A理论算法不适用于大规模电网GIC无功扰动的快速评估计算。与三相三柱、三相五柱的变压器相比，单相自耦变压器对GIC敏感[9]，抗直流偏磁的能力差。本文提出利用变压器厂家提供的U-I曲线建立变压器ψ-i曲线的解析模型，研究单相自耦变压器的GIC无功损耗算法，从而实现大规模电网GIC无功扰动的工程计算。

1 基于U-I曲线建立ψ-i模型

1.1 变压器U-I曲线特性

U-I曲线是指空载变压器电流均方根值Irms随电压均方根值Urms的变化曲线，可反映变压器的基本电磁关系[10]。作为变压器的励磁特性，U-I曲线由变压器的生产厂家提供，因此可以方便地获取U-I曲线来用于计算GIC无功扰动。

以单相双绕组为例，U-I曲线的数学模型表示为式（1）。

其中，u1为变压器一次绕组端口电压瞬时值，取均方根为Urms；i0为空载电流（励磁电流），取均方根为Irms；r1为一次绕组电阻；N1为一次绕组匝数；λm、λσ1分别为铁芯主、漏磁通的磁路磁导；μ为铁芯主磁路磁导率；S为变压器铁芯截面；l为铁芯主磁路长度。

GIC作用下μ非线性变化，进而导致λm呈非线性，则U-I曲线体现变压器非线性磁化特性。

1.2 ψ-i模型建立方法

计算变压器的直流偏磁效应，需要建立以电感形式表达的电路模型和进行非线性模型的迭代计算[8，11]，本文提出用投影法建立 ψ-i瞬时特性模型，并通过对参数选取，简化迭代计算。

1.2.1 ψ-i模型建立原理

ψ-i为磁链随电流瞬时变化曲线，U-I曲线到ψ-i曲线的转换以电压和磁通在频率正弦变化为前提。U-I曲线在正弦电压下获得，变压器直流偏磁时电压无畸变[12-13]，满足转换条件。

厂家提供的励磁特性参数常以数表表示，绘制的U-I曲线和ψ-i曲线如图1所示。其中，点1为线性区域到非线性区域的拐点。

图1 U-I和ψ-i对应图Fig.1 Corresponding relation between U-I and ψ-i curves

转换的方法及过程分电压转换和电流转换两部分，转换均以点对点转换方式进行。

电压有效值Urms到磁链ψ的转换如图2所示，由每个Urms值生成正弦变化曲线u=Urmssin θ，则u为时间 t（θ=ωt）的函数，ψ（t）为 u 的积分，因此也为时间t的函数。假设在每个转换点电压达到基波最大值，则可得ψ-i曲线中的ψ值。

图2 电压磁链转换原理图Fig.2 Schematic diagram of conversionfrom U to ψ

电压转换后可进行电流转换，电流有效值Irms到瞬时值i的转换如图3所示。ψ-i曲线为分段线性函数，ψ（t）为时间 t（θ=ωt）的函数，则 i为磁链 ψ 和时间t的复合函数。假设磁链ψ在需要转换的电流点达到基波最大值，则可得ψ-i曲线中的i值，转换忽略磁滞损耗和涡流损耗。

图3 电流转换原理图Fig.3 Schematic diagram of conversion from I to i

1.2.2 求解方法

电压有效值Urms到磁链ψ的转换基于电磁感应定律，则 ψk可由式（3）获得。

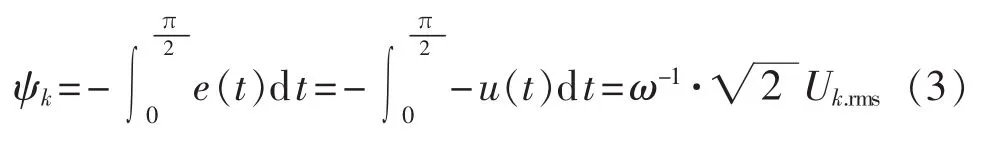
其中，k=1，2，3；ω=2πf，f为频率。

以转换点k=3为例进行电流转换求解ik，其他节点依此类推。 则可得对应的方程式（4）[14-15]。

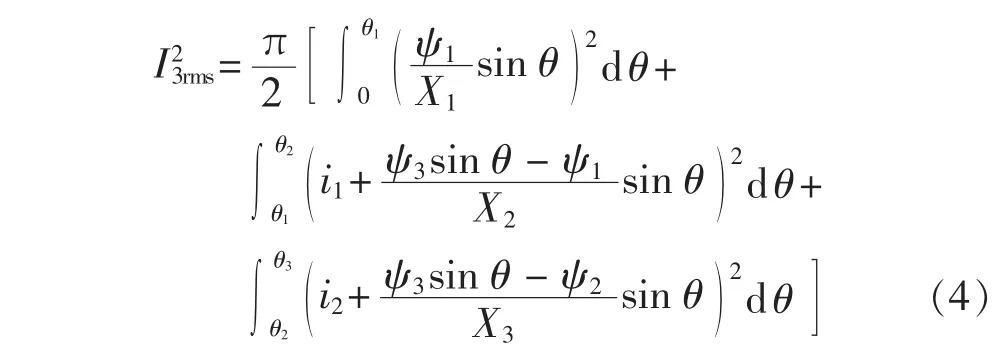
其中，X1、X2为 ψ-i曲线分段斜率，由已求得 ψ-i曲线段计算；X3见式（5）；θk见式（6）。

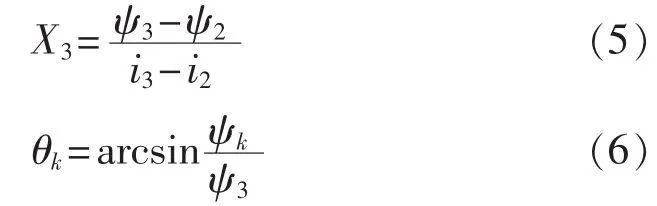
其中，i3为未知变量，i1、i2为已知，则方程式（4）—（6）构成非线性积分方程组。采用梯形积分公式可以提取出变量i3，整理成式（7），求取i3。本文梯形积分采用1°为步长。

其中，a、b、c为方程系数，提取i3后为已知值。

2 GIC无功损耗算法

GIC作用下变压器偏磁饱和，无功消耗增加与变压器的励磁电抗、漏抗等因素有关[16]，励磁电抗是主要因素。在本文无功损耗评估中，计算不同GIC大小下的励磁无功增额，以在电网运行和无功控制系统中考虑无功增额的影响。

2.1 变压器无功增大原理

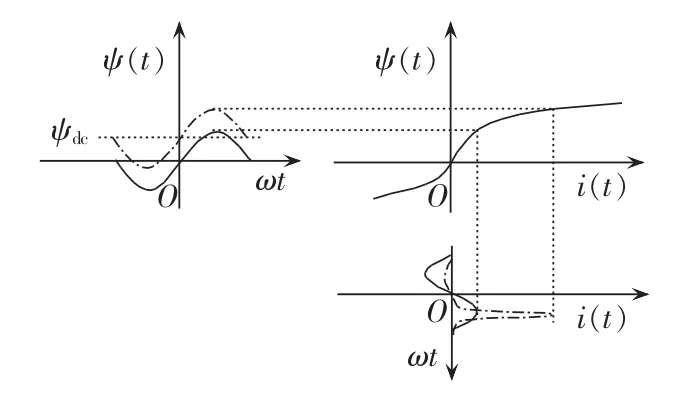
图4 GIC无功产生原理图Fig.4 Schematic diagram of GIC reactive power generation

地磁扰动产生地表电势差，使变压器磁通量单向增加，产生直流偏置磁链ψdc，导致变压器励磁电流波形畸变，如图4所示。畸变的励磁电流正包含直流、基波和谐波分量成分。其中，直流分量为地磁扰动产生的GIC，对应变压器的直流偏置磁链，基波和谐波分量对应正弦磁链[12]。由交流电压决定的正弦磁链相位滞后交流电压90°，为GIC作用下变压器的无功功率源。

因此，变压器GIC无功损耗计算评估的关键在于计算变压器励磁电流。其中，励磁电流的直流分量为流入变压器的GIC，GIC作用下的基波和谐波分量共同决定变压器的无功损耗。

2.2 投影法求励磁电流

变压器GIC直流偏置原因是：地磁暴感应地电势（ESP）在电网产生 GIC，即 Idc；Idc产生直流偏置磁通ψdc。其中，Idc可根据ESP大小和输电线路、中性点接地变压器和大地GIC回路的参数计算；ψdc可根据GIC回路参数对ESP分压，即作用在变压器的Udc大小计算。现有的基于磁电路模型的算法以Idc或Udc为设定参数，无法避免求解含非线性电感的微分方程以及迭代求解产生的计算量。本文用投影法求励磁电流。

取ψ-i为投影函数F，则地磁扰动发生时，变压器磁链和励磁电流满足方程式（8）：

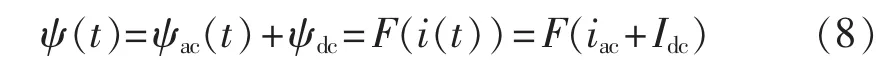
其中，ψac（t）为正弦磁链；ψdc为直流偏置磁链；iac为交流励磁电流；Idc为励磁电流的直流分量；F为ψ-i函数。

Idc和 ψdc不满足磁化曲线 ψ-i[17]，即：

方程式（8）中，ψac（t）、Idc为已知，ψdc、iac为未知。方程求解需设定初值进行迭代。

在计算上，本文提出采用设置一系列GIC偏置磁链的计算方法，求解设置的GIC励磁电流序列i（t），并进行快速傅里叶变换（FFT）分解及计算，可得到iac和Idc，进而求解一系列的Idc作用下的变压器GIC无功损耗。由于电网的规模大、变压器数量多，计算一系列Idc水平下的无功损耗，避免非线性微分方程迭代求解、降低计算量，是在线评估大电网GIC无功波动、电压波动需要考虑的问题。

2.3 变压器的GIC无功损耗算法

GIC作用下励磁电流发生畸变，无功损耗计算属非正弦无功范畴。对非正弦无功计算有2种典型方程[18]：，与经典有功功率计算方法对应，但物理意义不明确；，用于无功补偿装置的补偿无功计算，但没有第1种应用广泛。研究GIC作用下变压器无功损耗的目的是判断电网无功需求与校核无功补偿容量的不平衡度，评估电网无功波动及电压不稳定的安全风险，因此采用第2种无功损耗算法。由于GIC侵害下励磁电压只存在基波正弦电压，无功损耗算法可表示为：

其中，Q 为单一 GIC 水平下的无功损耗；Ei、Ii、φi分别为i次谐波的电压有效值、电流有效值、功率因数角；U50Hz、I50Hz分别为工频电压有效值、工频电流有效值。

2.4 自耦变压器的处理

对自耦变压器，由于原副绕组中有直流电流流通，式（8）中的Idc需按串联绕组和公共绕组流过的等效 GIC 计算[19]，等效 Idc为：

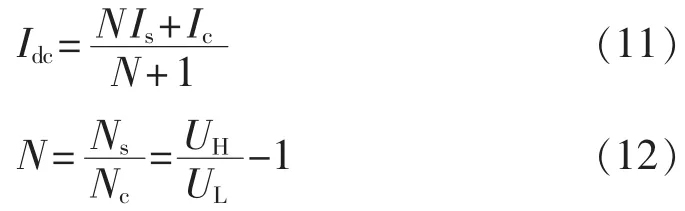
其中，UH、UL分别为额定电压和实际电压；Is为流过串联绕组的电流；Ic为流过公共绕组的电流；N为绕组匝数修正系数；Ns为串联绕组匝数；Nc为公共绕组匝数。

3 算例分析

3.1 计算流程

变压器GIC无功损耗计算依据以下步骤进行：

a.依据式（4）—（7），由 U-I曲线计算 ψ-i曲线，生成ψ-i曲线函数F以备调用；

b.输入偏置磁链序列，以k计数，依次提取磁链；

c.依据式（8），由投影法计算励磁电流，并进行FFT分解；

d.依据式（10）计算变压器无功并存储；

e.输出 Q、Idc、ψdc。

编制计算程序的流程图如图5所示。

3.2 模型参数

考虑未来的影响，本文取1000 kV单相自耦变压器ODFPS-1000000/1000为算例。

3.3 结果分析

3.3.1 计算结果

采用MATLAB编程，由变压器参数计算获得的ψ-i曲线数值如表2所示。由于U-I饱和段数据有限，文中对未给出数据的U-I采取线性差值。

图5 变压器GIC无功计算流程图Fig.5 Flowchart of GIC reactive power calculation for transformer

表1 1000 kV变压器U-I曲线Table 1 U-I curve of 1000 kV transformer

表2 1000 kV变压器ψ-i曲线计算值Table 2 Calculative ψ-i curve of 1000 kV transformer

表3 无功损耗计算结果Table 3 Results of reactive power loss calculation

表3给出了无功损耗的计算结果。可看出，随着GIC增大，无功损耗增大，两者近似呈线性关系。

以0Wb和200Wb为典型磁链偏置，计算结果分别如图6和图7所示。正常运行时磁链偏置水平为0 Wb，励磁电流基本正弦变化。磁链偏置为200 Wb时，励磁电流发生畸变，励磁脉冲特性明显，计算结果与原理分析对应良好。

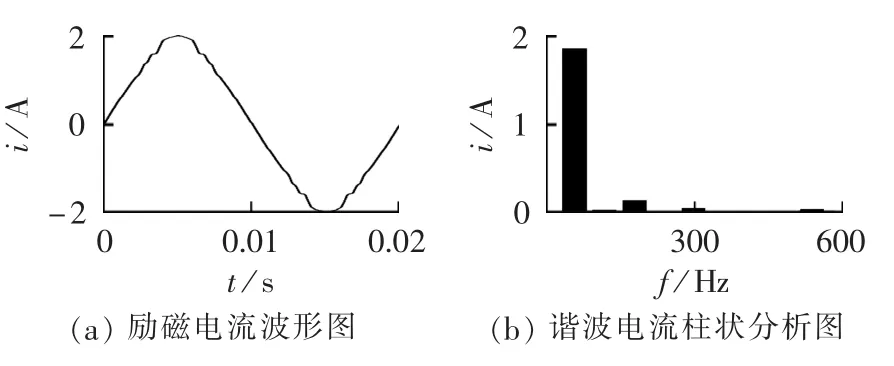
图6 偏置磁链为0 Wb时励磁电流分析结果Fig.6 Analytical results of exciting current when DC flux is 0 Wb

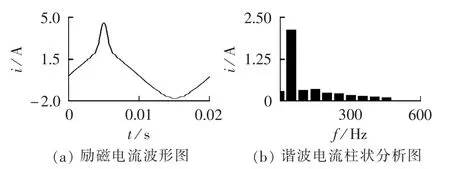
图7 偏置磁链为200 Wb时励磁电流分析结果Fig.7 Analytical results of exciting current when DC flux is 200 Wb

3.3.2 误差分析

当磁链偏置为0 Wb时，励磁电流最大幅值为Im=1.9830 A，基波幅值为If=1.8430 A。忽略因ψ-i线性差值产生的轻微畸变，取基波电流作为励磁电流的等效正弦波，计算有效值。变压器厂实测空载电流百分比为0.075%，误差分析如下：

当磁链偏置为200 Wb时，励磁电流最大幅值为Im=4.5030 A，基波幅值为If=2.1132 A。200 Wb对应的Urms值计算如下：

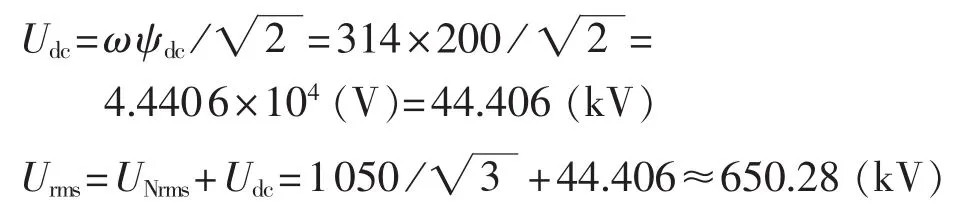
则可由U-I曲线获得200 Wb对应电流有效值为Irms=1.9499 A。励磁电流曲线计算有效值Irms.j和误差分析如下：

其中，I0为直流电流有效值；I1、I2分别为基波和2次谐波有效值。

这一误差包含了对U-I曲线数据点进行分段线性化处理的误差，线性化处理使励磁电流畸变量微增，而偏置为0 Wb时，磁化曲线本身处于线性段附近，线性化引起的畸变量较小。若扣除线性化误差，仅考虑U-I到ψ-i数据点转换误差，应与5.35%不相上下。

表3计算结果为：磁链偏置为0 Wb时，空载无功损耗为0.79 Mvar，与实测空载无功损耗0.75 Mvar结果相近，其中实测空载无功损耗Q0忽略了磁滞和涡流损耗。

4 结论

电网规划、运行GIC影响评估需要简单、实用的变压器GIC无功损耗模型及其算法。本文利用变压器厂家提供的U-I曲线值计算单相自耦变GIC空载无功损耗，得到结论如下。

a.利用变压器U-I曲线建立磁化ψ-i曲线模型，以及采用投影法求励磁电流和设置一系列偏置磁通的算法，针对1000 kV单相自耦变算例计算误差约为±5.35%。结果表明，利用U-I曲线建立的磁化ψ-i曲线模型计算变压器的GIC无功损耗，能满足电网规划影响评估的需要。

b.采用J-A理论方法计算变压器铁芯磁化特性，评价变压器直流偏磁效应精度高，但获取设计参数和模型建立困难，同时变压器结构、类型复杂，迭代计算量大，不适用于电网工程GIC影响的评估计算。本文模型容易获得，算法简单和计算量小，是GIC影响评估的实用算法。

c.由于不同结构不同厂家变压器的U-I曲线存在一定的差异，虽然可采用本文相同的U-I曲线转换为ψ-i曲线的方法，但如何处理大量变压器海量数据，实现大规模电网无功及电压波动的计算，以及考虑磁滞损耗和涡流损耗对全网评估的影响等，都是下一步考虑的问题。