高压直流输电系统开路电压的研究

2015-09-20李永丽李博通

电力自动化设备 2015年11期

张烁，李永丽，李博通

（天津大学电力系统仿真控制教育部重点实验室，天津 300072）

0 引言

高压直流输电因其在远距离、大容量输电方面的优势，近年来在国内得到了大力发展。截至2013年底，我国已建成超、特高压直流输电线路20余条，高压直流输电正逐渐成为未来我国跨区域大容量输电的重要方式[1-6]。

直流开路试验OLT（Open Line Test）又称空载加压试验（以下简称开路试验），是检测换流阀及直流场设备、直流控制系统、直流输电线路能否正常工作的重要手段。直流系统在设备检修或长时间停运后，都必须通过开路试验才具备正式送电条件[6-7]。在开路试验过程中，操作人员通过控制换流器触发角，使测量电压（即开路电压）按一定变化率逐渐升高，并通过观察测量电压能否逼近预设的目标电压来判断各设备的工作状况是否正常。开路试验目标电压根据开路电压理论值选定，因此，开路电压计算公式的准确性对于试验成功与否至关重要。

根据检测对象的不同，开路试验可分为不带直流线路和带直流线路2种。从试验系统结构上看，2种开路试验的区别仅在于直流线路侧开路点位置不同，不带直流线路开路试验开路点设在直流线路首端，主要用于检测换流阀及直流控制系统的工作状况；带直流线路开路试验的开路点设在直流线路末端，除了检测换流阀及直流控制系统的工作状况外，还可用于检测直流滤波器等直流场设备及直流线路的绝缘水平和耐压能力。对于不带线路开路试验，ABB公司推导了其开路电压计算公式（以下简称为现有公式），并依此设计了开路试验电压差值保护，保护动作于开路电压测量结果与计算结果之差大于动作门槛值（±500 kV系统的动作门槛值为150 kV）。而对于带直流线路开路试验，由于目前尚未有机构或个人给出其开路电压的推导公式，因此，在实际试验中也是利用现有公式计算其目标电压。但是根据实际试验结果，带直流线路开路试验的开路电压与不带线路时相比明显减小[9-10]，若利用现有公式计算其目标电压，则测量电压与目标电压之间将存在较大差值，可能造成电压差值保护误动，进而闭锁试验系统[11-13]。文献[14-15]结合实例，对带直流线路开路试验中测量电压较低的原因及现有公式的适用范围进行详细分析，但并未给出具体的带直流线路开路电压计算公式。文献[16]通过对带直流线路开路试验中线路元件充放电过程进行讨论，给出了带直流线路开路电压计算公式。但所提公式中需要利用线路对地电导等参数，其数值受气候环境影响大，很难应用于工程实际。

鉴于带/不带直流线路开路试验系统仅在是否包含直流线路上存在区别，本文借鉴不带直流线路开路电压公式的推导方法，通过分析直流设备及线路元件对开路电压的影响，确定带直流线路开路电压的稳定条件，并通过对现有不带直流线路开路公式进行修正，给出适用于带直流线路开路试验的开路电压计算公式。利用PSCAD仿真软件搭建了直流输电系统的仿真模型，对改进公式进行了仿真验证，仿真结果验证了所提公式的准确性。

1 不带直流线路开路试验开路电压公式的推导

超高压直流输电系统多采用12脉动换流器，12脉动换流器由2个6脉动换流器串联构成，在不带线路开路试验中其开路电压等于6脉动换流器的2倍，因此，为了简化分析过程，下面以6脉动整流器为研究对象进行不带直流线路开路试验开路电压公式推导，其开路试验系统示意图如图1所示[3]。

图1 不带直流线路开路试验系统示意图Fig.1 Schematic diagram of OLT system without DC line

图中，EA、EB、EC为换流变压器阀侧三相感应电动势；UA、UB、UC为换流变压器阀侧三相端电压；Lγ为换相电抗；UDC为开路电压；UN为换流变压器阀侧中性点电压。VT1—VT6为晶闸管换流阀，换流阀两端并接有 RC缓冲电路；阀 VT2、VT4、VT6阳极共点于Q点，称为共阳极阀组；VT1、VT3、VT5阴极共点于 P 点，称为共阴极阀组。

假设换流变压器阀侧交流系统三相对称，线电动势有效值为E，根据换流原理，换流器的自然换相点为交流线电压过零点，因此，为了方便描述换流器导通触发角，以线电动势ECA正向过零点为坐标原点建立坐标系，换流变压器阀侧各相交流相、线电动势的波形图如图2所示。

图2 换流变压器阀侧各相理想电动势波形图Fig.2 Ideal valve-side electromotive force waveforms of converter transformer

换流变压器阀侧各相感应电动势表达式为：

由图1可知，开路电压UDC可表示为：

由于Q点接地，UQ=0，因此，UDC=UP。又由于直流线路侧开路，UP幅值大小仅受换流阀通断状态的影响，在共阴极组任意换流阀导通时满足：

其中，x表示与导通阀相连的交流侧某相。因此，为了求取UP表达式，以下对各换流阀通断期间UP的变化情况逐一进行分析。

先以VT1为例，在VT1首次导通前，在三相对称电压的作用下，P、Q 2点的初始电压UP、UQ及换流变压器阀侧中性点电压UN均等于0。此时VT1的阴极电压等于0，阳极电压等于EA，忽略阀导通/关断固有时间的影响，结合图2可知，若换流阀触发角α小于 150°，在 VT1触发时刻有 UA＞0，VT1导通，忽略阀上压降，在 VT1导通后，根据式（3）有：

根据晶闸管导通条件，晶闸管在承受反压后关断，因此，VT1将导通至其阳极电压单调递减为止。结合式（1），若 ωtє[0°，60°），EA递增，在此期间触发VT1，VT1导通至 ωt=60°时关断，关断后 VT1的阴极电压 UP=EA（60°）；若 ωtє（60°，150°]，UA递减，在此期间触发VT1，VT1会在导通后随即便因承受反压而关断，关断后 VT1的阴极电压 UP=EA（α）。

根据直流输电换相原理，VT2在VT1触发1/6工频周期后触发。与VT1分析过程相同，若触发角小于 150°，VT2导通。VT2导通后，根据其阴、阳极电压相等有：

因此：

可见，在VT2导通之后，UN不再为0，且在VT2导通期间 UN随 EC变化。根据图2，若 ωtє[60°，120°），EC递减，在此期间触发 VT2，VT2将导通至 ωt=120°时关断，关断后 UN=-EC（120°）=EA（60°）；若 ωtє（120°，210°]，EC递增，在此期间触发 VT2，VT2会在导通后随即便因承受反压而关断，关断后 UN=-EC（α+60°）=EA（α）。因此在 VT3触发时其阳极电压等于 UN+EC（α+60°）=2UP，大于其阴极电压 UP，VT3可导通，之后的分析过程与VT1相同，可推导出在VT3关断后UP表达式为：

VT4、VT6导通期间的分析过程与VT2相同，由于交流侧三相电压对称，各阀导通期间所确定的UN相等，UN波形近似为一条直线，但受换流变压器铁芯饱和等因素的影响，UN中含少量谐波，以3次谐波为主[17]。图3为触发角α=120°时UN的仿真波形。

图3 α=120°时，不带直流线路开路试验的UN波形Fig.3 UNwaveform of OLT without DC line when α=120°

理想条件下，在VT3关断后，UP将保持不变，但是由于均压、缓冲电路的影响，UP实际呈缓慢衰减状态[10]（由于电压衰减速度很慢，在计算开路电压时可忽略），而根据换流原理，共阴极组各阀导通时刻对应的交流相电压瞬时值相等，大于此时VT5的阴极电压UP，VT5满足导通条件。VT5通断期间的分析过程与VT3相同，UP的幅值和变化规律也均与式（7）相同，各阀不断重复以上过程，得到UP波形如图4所示。

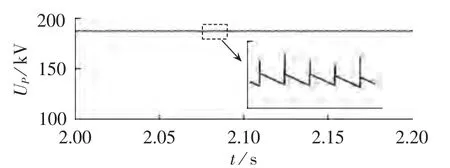
图4 α=120°时，不带直流线路开路试验的UP波形Fig.4 UPwaveform of OLT without DC line when α=120°

将式（7）代入式（2）即得到不带直流线路条件下6脉动换流器开路电压计算公式，12脉动换流器开路电压等于6脉动换流器的2倍，因此，最终得到超高压直流输电系统不带直流线路开路试验开路电压公式（即现有公式）为：

2 带直流线路开路试验开路电压的建立过程分析及公式推导

2.1 带直流线路开路电压的建立过程分析

以上分析了不带直流线路开路电压的推导过程，对于带直流线路开路试验，由于换流系统结构及控制方式与不带直流线路时完全相同，因此，可以借鉴以上推导思路用于带直流线路开路电压的分析。仍以6脉动系统为研究对象，将图1所示系统开路点从线路首端移至线路末端即为带线路开路试验系统，6脉动换流器带直流线路开路实验系统示意图如图5所示。

图5 带直流线路开路试验系统示意图Fig.5 Schematic diagram of OLT system with DC line

在接入直流线路后，换流器与直流线路及直流滤波器（DCF）支路可以通过大地构成回路，带直流线路开路试验系统等效示意图如图6所示。

图6 带直流线路开路试验系统等效示意图Fig.6 Equivalent schematic diagram of OLT system with DC line

根据仿真实验结果，线路模型采用集中参数或分布参数对开路电压基本无影响，因此，为了简化分析过程，本文采用输电线路集中参数。图6中，R、L、G、C分别为直流线路的电阻、电感、电导、电容；Ls为平波电抗器；DCF为三调谐直流滤波器；Re为接地极线路阻抗；IDC为开路电流；IDCF为直流滤波器支路电流；Iline为直流线路电流；UDC为开路电压；UDCF为直流滤波器支路电压，由图可知UDC=UDCF。

根据之前的分析，在开路试验过程中换流阀导通时间很短，在试验中的任意时刻换流器至多有1个阀导通。在所有换流阀均关断时，交流线路通过各换流阀的缓冲电路与直流线路侧相连，由于交流系统对称，所以开路电流IDC约等于0；而在某一换流阀导通时，系统对称被打破，换流阀直流侧出口线路上有电流流过，电流持续时间等于换流阀的导通时间，在阀关断后系统恢复对称状态，IDC再次衰减至0，之后IDC以换流阀触发间隔为周期不断重复上述过程。

在阀导通阶段，IDC中的直流分量只能通过对地电导支路，而对地电导支路的阻值极大，所以IDC中直流分量所占的比例很小。又根据换流原理，6脉动换流器仅在直流侧产生 6n（n=1，2，3，…）次谐波[2]，因此，此时的IDC主要由6n次谐波构成。如图6所示，DCF支路与直流线路并联，根据IDC的频率特性，对于IDC而言，DCF支路的阻抗比直流线路小得多，因此，IDC≈IDCF。带直流线路开路试验触发角α=120°时的开路电流IDC、直流滤波器支路电流IDCF、直流线路电流Iline仿真波形如图7所示，图中t1—t6、t′1—t′6分别对应 6个换流阀的触发和关断时刻。

图7 α=120°时，带直流线路开路试验的IDC、IDCF和Iline仿真波形Fig.7 Simulative waveforms of IDC，IDCFand Ilineof OLT with DC line when α=120°

图7反映了直流线路侧各支路电流在开路电压稳定后某一工频周期内的变化情况，如图所示，IDC与IDCF波形近似重合，两者均在换流阀导通时突然正向增大并随着换流阀的关断再逐渐衰减为0。由于开路电压已经趋于稳定，故Iline波形近似为一条直线且幅值很小，仿真结果与之前的分析相吻合。

根据上述的直流线路侧电流分布特征，在换流阀导通阶段由交流侧向直流侧注入的能量只会有少部分以热能的形式消耗在对地电导上，而绝大部分能量将流入DCF支路为其支路电容充电，UDCF随之逐渐升高。在换流阀关断后，IDC反向且幅值逐渐衰减为0，交流系统不再向直流线路侧输送能量，DCF支路电容开始向对地电导支路放电，UDCF下降，至下一个换流阀导通为止。由于触发角固定，DCF支路电容在每周期内的充放电时间固定，在试验开始阶段，由于UDCF较低，对地电导支路在阀关断期间消耗的能量小于DCF支路电容在阀导通期间吸收的能量，UDCF不断升高，如图8（a）所示。但随着UDC的升高，DCF支路电容每周期内吸收的能量越来越少而对地电导支路消耗的能量却不断增多，UDC升高的速度逐渐放缓，当UDCF在每周期内升降的幅值相等后，UDCF达到稳态，如图8（b）所示。

图8 α=120°时，带直流线路开路试验的UDCF仿真波形Fig.8 Simulative waveforms of UDCFof OLT with DC line when α=120°

根据图6，UDCF=UDC。因此，由上所述，在带直流线路开路试验中，开路电压从建立到稳定之间存在暂态变化过程，当DCF支路电容在开路电压单个变化周期内充放电能量达到平衡时开路电压趋于稳定。相比于不带直流线路开路试验，因为在换流阀关断期间存在降压过程，所以，带直流线路开路试验开路电压的稳态值比不带直流线路开路试验中的开路电压小。

2.2 带直流线路开路试验开路电压公式推导

2.2.1 6脉动换流器带直流线路开路电压公式的推导根据2.1节的分析，计算开路电压最直接的方法就是利用电压稳定后DCF支路电容在单个电压变化周期内充放电能量平衡这一结论，列写关系式以求解开路电压。但是由于直流系统的非线性特征，换流器的等效模型难以确定，且无法应用相关电路原理。同时换流阀导通期间的直流线路电流为冲击电流，很难写出其具体表达式，而对地电导参数又极易受环境影响，因此，利用单个电压变化周期内充放电能量平衡特征推导开路电压计算公式是不可行的。

值得注意的是，对于带直流线路开路试验，在换流阀导通阶段，仍有式（2）、（3）成立，即：

因此，可以通过求解UN确定UDC。在不带直流线路试验中，UN波形近似为一条直线，如图3所示。在带直流线路开路试验中，共阳极组阀导通时UN变化情况与不带直流线路时相同，而在共阴极组阀导通时，由于开路电压比不带线路时小，UN也比不带直流线路时小，所以在带直流线路开路试验中UN波形近似为矩形波。对于6脉动换流器，UN变化周期为1/3工频周期，在每个周期内UN跳变2次，跳变时刻对应于换流阀导通时刻，共阳极组阀导通时UN由低电位跳变至高电位，共阴极组阀导通时UN由高电位跳变至低电位。

带直流线路开路试验触发角α=120°时的UN仿真波形如图9所示，图中tc1—tc6分别对应6个换流阀的触发时刻。

图9 α=120°时，带直流线路开路试验的UN波形Fig.9 UNwaveform of OLT with DC line when α=120°

综上所述，2种开路试验中开路电压幅值不等的原因也可以理解为：对于2种开路试验，在共阴极组阀导通时刻，换流变压器阀侧中性点电压并不相等。

因为在换流阀交流侧，UN满足：

所以，可以利用交流侧三相相电压求解UN。如图9所示，共阴极组阀导通时UN跳变至低电平，因此，对于矩形波UN，求解开路电压需要利用的是其极小值UNmin。在本文中，UNmin的求取方法为：以UN变化周期为采样窗长，取交流侧三相相电压数据代入式（10）计算UN，并由低电压采样数据的平均值求取UNmin。在确定了UNmin后，带直流线路开路试验中开路电压可以表示为：

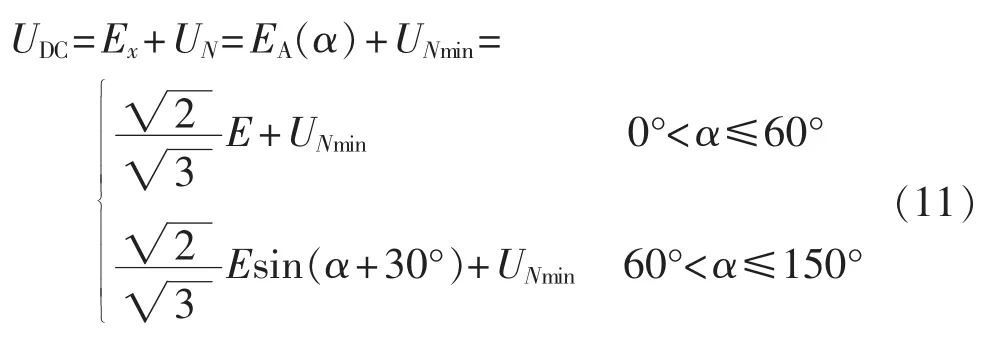
2.2.2 12脉动换流器带直流线路开路电压公式的推导

对于12脉动换流器，其系统示意图如图10所示。

图10 12脉动换流器带直流线路开路试验系统等效示意图Fig.10 Equivalent schematic diagram of OLT system with DC line for 12-pulse converter

根据系统结构，Umid即为桥2的输出电压，因此，下面以其为研究对象，分析在12脉动系统中6脉动换流器的输出电压特征。

根据前文的分析可知，无论带直流线路与否，在开路试验过程中，受触发角大小影响，换流阀的导通时间均很短，当触发角大于60°时，换流阀在导通后随即便会因承受反压而关断。因此，在试验任意时刻，换流系统中至多有1个换流阀导通，且在试验的绝大多数时间内，系统中的所有换流阀均处于关断状态，在此期间，由于换流系统结构对称，交直流系统间无能量传递，开路电压保持不变。而在有换流阀导通期间，由于系统对称结构被破坏，交直流系统间可能出现能量传递。

对于不带直流线路开路试验，由于直流线路侧开路，即使在换流阀导通期间，交直流系统间仍基本无能量传递，开路电压仅由换流阀触发时刻的交流相电压决定。在所有换流阀均关断期间，开路电压仅存在缓慢的衰减过程，幅值基本保持不变。在某一换流阀导通期间，若换流阀位于桥2，则桥1各阀均关断，桥2与直流侧只能通过桥1换流阀的缓冲电路相连接，桥1等效于1个RC串联支路，此时的12脉动开路系统等效于在6脉动开路系统的开路端串联进1个RC串联支路，但由于直流侧开路，RC支路显然对开路电压无影响，Umid与6脉动带直流线路开路试验中开路电压值相等。

若导通的换流阀位于桥1，由于此时系统中仍无能量变化，所以桥1中某一阀导通，仅相当于改变了串联RC元件的数值，对Umid无影响。同理可得，另一个6脉动换流器的输出电压也与6脉动开路试验时相等。综上，在12脉动不带直流线路开路试验中，2个6脉动换流器的输出电压与6脉动不带直流线路开路试验中的开路电压相等，因此，12脉动不带直流线路开路试验的开路电压可以按6脉动换流器开路电压的2倍近似进行计算。

而对于带直流线路开路试验，当桥2中某一阀导通时，桥1等效为RC支路，串接于桥2与直流线路之间，如图11（a）所示。由于此时换流阀通过线路及换流阀的接地点构成回路，所以此时RC上存在一定压降，造成Umid比6脉动带直流线路开路电压小，两者的差值受RC参数影响。

图11 12脉动换流器中的部分阀导通时带直流线路开路试验系统等效示意图Fig.11 Equivalent schematic diagram of OLT system with DC line when partial valves of 12-pulse converter are turned on

当桥1中某一阀导通时，桥2各阀均处于开路状态，相当于将RC支路串接在桥1与接地点之间，如图11（b）所示。此时的Umid等于RC支路上的压降，根据换流器结构，显然2种情况下得到的Umid的幅值大小并不相等。

综上所述，对于12脉动换流器，在直流线路进行开路试验时，桥2的输出电压波形不再近似为直线型，而是变为矩形波，输出电压每隔30°跳变一次，下降沿对应桥1中换流阀导通时刻，上升沿对应于桥2中换流阀导通时刻。触发角α=120°时的Umid仿真波形如图12所示，图中1—6表示桥1中各阀的导通时刻，1′—6′表示桥2中各阀导通时刻。

图12验证了上述分析的正确性，由于桥1和桥2仅在换流变压器接法上有区别，其他结构完全相同，所以桥1的输出电压波形与桥2相同，仅在相位上相差30°。由于2个输出电压之间的相位差与输出电压的跳变间隔相同，因此，其中一桥的输出电压为高时另一桥的输出电压为低，如图13所示，其中UDC1表示桥1输出电压，UDC2表示桥2输出电压。又由于12脉动换流器的开路电压等于两桥输出电压之和，所以，测得的12脉动换流系统开路电压约等于Umid的高电压和低电压之和。

图12 α=120°时，带直流线路开路试验所得的12脉动换流器Umid仿真波形Fig.12 Simulative waveform of Umidof OLT with DC line for 12-pulse converter when α=120°

图13 α=120°时，带直流线路开路试验所得的12脉动换流器桥1、桥2输出电压波形Fig.13 Output voltage waveforms of bridge 1 and 2 of OLT with DC line for 12-pulse converter when α=120°

根据前文的分析，桥1、桥2中换流阀导通时刻的Umid幅值不同，设桥2中换流阀导通时的Umid幅值用Umid_h表示，桥1中换流阀导通时的Umid幅值用Umid_l表示。如图12所示，由于桥2中各阀导通时得到的高电压均相等，因此，任意选取其中一阀作为研究对象，以阀 V′T1为例，在阀 V′T1导通时有：

其中，UNdn=（U′A+U′B+U′C）/3 为桥 2 换流变压器阀侧等值中性点电压。

同理，对于桥1取阀2为对象，设桥1换流变阀侧中性点电压为UNup，则在阀2导通时有：

因此，12脉动带直流线路开路试验的开路电压计算公式为：

将式（1）代入式（14）得：

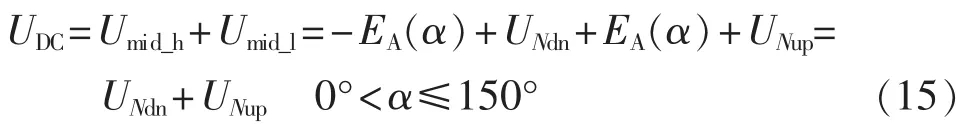
根据仿真结果，用UNup_min表示UNup的极小值；用UNdn_max表示UNdn的极大值，则12脉动带直流线路开路试验的开路电压等于：

超高压直流输电系统带直流线路开路试验的开路电压可以按式（16）进行计算，UNup_min和 UNdn_max的求解过程与2.2.1节中UNmin的求解过程相同。

3 仿真验证

为了验证所提公式在实际带直流线路开路试验中的计算准确性，参照高坡—肇庆±500 kV超高压直流输电系统，利用PSCAD搭建超高压直流输电系统仿真模型对所提公式进行了仿真验证。模型参数依据高坡—肇线实际参数设定，线路长度取891 km，单位长度线路参数根据架空线参数求得，对地电导参数为皮克公式推算结果，具体参数如表1所示，参数定义与图5相同。