基于误差修正的短期负荷预测方法

张 贲，邵常宁，赵 燃

（1.国家电网公司华北分部，北京 100053；2.北京清软创新科技有限公司，北京 100085）

0 引言

短期负荷预测是电力系统运行的重要辅助决策手段，为电力调度部门安排日发电计划、机组组合、优化潮流以及经济调度提供科学依据，对于保障国民经济安全运行有重要意义。

多年来许多学者对短期负荷预测进行了深入的研究，提出了大量的预测方法。这些方法从机理上大体可分为2类：基于趋势外推思想的数学算法和考虑相关因素的智能算法。基于趋势外推思想的算法主要包括倍比平滑法、时间序列法、回归模型法等[1]，这些方法以探究负荷本身的发展规律为思想进行预测，大多数以线性模型为主。外推方法在相关因素影响弱的地方能取得不错的效果，但遇到相关因素变化剧烈的地方精度会变得很差，而且无法处理非线性问题。考虑相关因素的智能算法主要包括模糊逻辑法、人工神经网络（ANN）[2]和支持向量机（SVM）[3]等。这些方法是将经过自适应训练[4]后的相关因素量化参数作为输入，建立庞大的非线性映射模型进行运算，能够得到比较精确的预测结果。但其缺点为在数据处理、函数构造、参数优化等方面难度较大，一定程度限制了其应用。

一般而言，传统外推方法能够基本体现刨除未知因素之外用户的用电习惯和负荷规律，预测结果与实际负荷之间的误差与相关因素会有着强烈的依赖关系。对于特定地区而言，在一段时间内某些相关因素的影响可能会稳定存在[5]。本文所采取的思路即通过对历史负荷预测误差的研究建立误差与相关因素的合理映射，从而对未来负荷预测进行修正以达到提高预测精度的目的。

1 误差修正总体思路及方法准备

误差修正预测总体思路可以分为基于频域分解法虚拟预测、建立误差与相关因素映射、预测结果修正3个阶段，如图1所示。

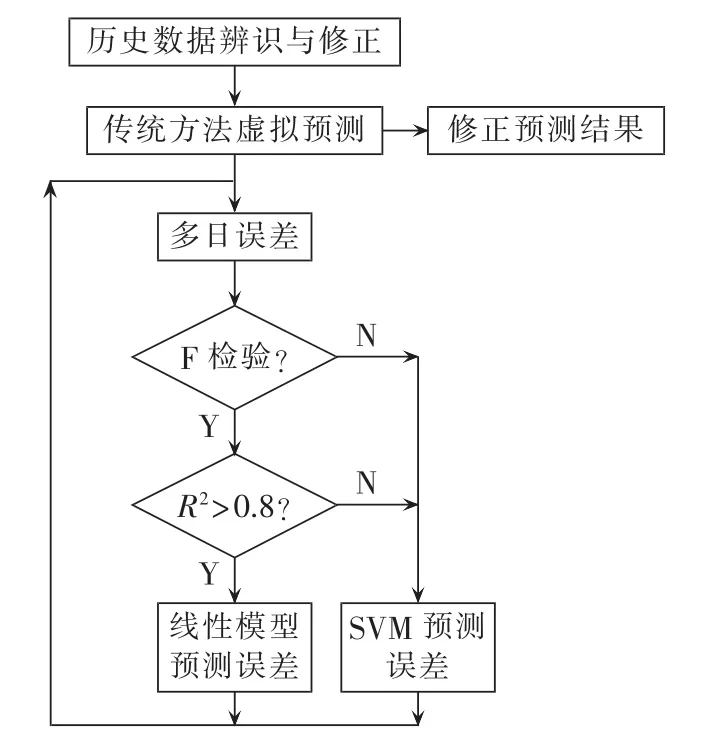
图1 误差修正预测总体思路Fig.1 General concept of forecasting with deviation correction

首先对采集到的历史负荷、气象数据进行预处理以提高数据质量，然后利用传统频域分解预测方法进行虚拟预测，与实际负荷相比得到多日预测误差。对预测误差与气象指标进行线性检验，根据相关特性采取相应的回归模型进行误差预测，并对传统方式的预测结果进行修正。在建立误差预测流程前需要进行以下几个部分的准备工作。

1.1 虚拟预测

虚拟预测是负荷预测研究的常用手段，通过历史负荷及相关因素（例如气象）数据对已知负荷日进行假定的预测，通过虚拟预测的结果和历史实际负荷的对比分析研究预测的精确度，探究影响预测精度的原因等。

1.2 历史不良数据辨识与修正

丰富而准确的历史数据是负荷分析和预测工作的前提，预测前有必要对历史不良数据进行辨识与修正。文献[4]提到了几种常用的不良数据辨识修正方法，包括神经网络法、基于聚类分析及模糊理论的方法、间隙统计法（GSA）、残差修正法等[6]，主要针对大量历史数据的自动辨识修正。本文研究的历史样本仅为一个月，数据较少，采取如下的简单辨识方法。

a.确定历史样本。

设历史样本第 i天 t时刻的负荷为 Pi，t（i=1，2，…，n；t=1，2，…，T），n 为历史天数，T 为采样点数。第s天为第i天的同类型日，s=i±7，则其t时刻的历史负荷为 Ps，t。

b.逐点计算负荷偏差率：

设定偏差率的阈值为30%，超过阈值则视为不良数据需进行修正，不超过阈值则视为有效数据。

c.不良数据校正。

采取相邻2点的负荷偏差率平均值作为校正偏差计算本点修正数据，计算公式如下：

1.3 综合气象指数

气象因素的变化是影响负荷需求变动的重要因素，与预测误差具有内在关联性。通常人们对外界冷热干湿的感觉是在温度、湿度及风力等多种气象因素的综合作用形成下，单一气象指标无法准确描述人体的真实感觉。因此很多学者前后提出了许多考虑多个气象因素的综合气象指数模型，如实感温度、温湿指数、风冷力指数、人体舒适度等[7]。本文所涉及的综合气象指标主要有以下3个。

a.实感温度指数。

实感温度是指人体在不同气温、湿度和风速条件下，所产生的热感觉指标。实感温度以静止饱和的大气（风速为0时，相对湿度为100%）条件下使人产生舒适的温度，来代表不同风速、不同相对湿度、不同气温使人产生的同样感觉。计算公式如式（1）所示。

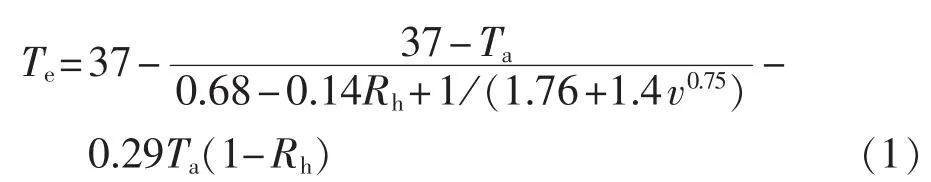
其中，Te、Ta、Rh、v 分别为实感温度（℃）、气温（℃）、相对湿度（%）、风速（m/s）。

b.温湿指数。

温湿指数是考虑温度和湿度2种气象因素的综合气象指标，计算公式如下：

其中，ET为温湿指数（℃）；Td为 14∶00 的温度（℃）；Rd为 14∶00 的相对湿度（%）。

c.舒适度指标。

舒适度指数是度量温度、湿度、风速等气象要素对人体的综合作用，表征人体在大气环境中舒适与否的综合指标。其计算公式为：

其中，k为人体舒适度指数。

上述3种综合气象指标各有侧重，需要根据地区的地理和气候特点选取科学权重进行建模。

2 误差修正具体流程

2.1 基于频域分解法的虚拟预测

电力负荷是具有较强周期性的时间序列，因此可以通过时间序列的频域分解方法进行分析[8]。设多日（一般取 14 d）的持续负荷序列为 P（t）（t=1，2，…，nT），对其作离散傅里叶变换（DFT）可得：

由离散傅里叶变换求得系数ai、bi，得到负荷序列分解后的一系列相互正交的正余弦分量和直流分量。根据频谱特征提取出不同的频率分量，通过离散傅里叶逆变换（IDFT）将其还原到时域，并通过适当组合重构出下式：

其中，日周期分量 a0+D（t）和周周期分量 W（t）为标准的周期序列，体现了人们不受干扰的规律性用电特征，预测时可以直接外推获得；L（t）为低频分量，体现了变换速度缓慢的相关因素对负荷的影响，可以通过建模的方式作逼近预测；H（t）为高频分量，体现了电力负荷的随机波动，具有不可预测性。

剩余分量处理方法为低频分量平滑方式[9]，即待预测日t时刻的低频分量为同一时刻各天历史负荷低频分量的一次指数平滑结果。

设平滑系数为 αє（0，1），根据“近大远小”原则可将历史上第j天的权重设定为αn-j+1，可得归一化的权重为，则待预测日t时刻的低频分量预测值为：

忽略高频分量可得待预测日的预测结果：

其中，a0+Ds，t、Ws，t分别为待预测同类型日的日周期分量、周周期分量。

2.2 建立误差与相关因素映射

传统频域分解预测方法产生误差的主要原因为低频分量预测不准和高频分量的忽略。高频分量属于噪声分量，不可预测且含量小，可不予处理；目前所采取的低频分量的预测方法主要有平滑方式、相关方式等，均无法跟踪相关因素的变化而导致预测效果较差。考虑到相对于某个特定地区而言在一段时间内某种相关因素的变化会遵循一定规律，而预测的误差也会随之呈现稳定的变化趋势，因此通过虚拟预测可以建立相关因素与误差的映射。

第i天t时刻预测误差为实际负荷与频域分量法（低频分量平滑方式）的差值：

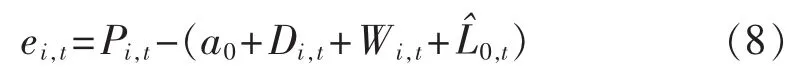
设第i天第m种相关因素的映射值为xi，m，这里的映射值是指通过摄动方式进行自适应训练得到的最优值，具体训练方法见文献[3]所述。以气象因素为例，很多情况下由于条件限制无法得到逐时气象信息，而只能得到某一天的气象特征指标，如最高温度、平均温度、风速、相对湿度等。由式（1）—（3）可以得到单一气象因素与综合气象指标的非线性映射为：

其中，yi，1、yi，2、yi，3分别为实感温度、温湿指数与人体舒适度指数。为了与误差建立一一对应关系，需要对每天的逐点误差进行标幺化处理，恰当地选取误差的基值Ei。建立误差基值与综合气象指标的数学映射如式（10）所示。

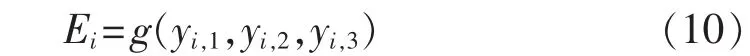
由上式得到综合考虑3种综合气象指标的线性回归模型，每种指标的回归系数即反映了该气象综合指标在该地区和特定时间段的合理性。

通过回归分析可以检验映射模型的线性度。以线性相关系数R2=0.8为检验标准，如果拟合系数大于0.8并且通过F检验，可以认为是线性模型进行多元线性回归分析；如果拟合系数小于0.8或者没有通过F检验，则视为非线性模型，采取支持向量机回归分析。

支持向量机是由Vapnik等[10]提出的统计理论中发展而来的。大量研究显示支持向量机能够弥补ANN、模糊逻辑等人工智能算法的网络结构复杂、训练时间长的不足，在处理小样本、非线性、高维数等实际问题时具有优势，可以建立完善的非线性负荷预测模型。支持向量机的具体算法参见文献[11]，这里不再赘述。

对于大部分地区而言，在气象平稳的春冬季传统预测方法精度足够高，而在气象剧烈变化的夏季预测精度较低，预测误差与气象因素会呈较强的线性相关特性。绝大多数情况下利用多元线性回归分析即可得到拟合精度良好的线性模型，使问题得到简化。

2.3 预测结果修正

预测结果修正可以按以下步骤进行。

a.传统预测结果处理。

b.待预测日误差基值预测。

设当日预报气象因素映射值为 x0，1、x0，2、…、x0，m，根据 2.2 节得到综合气象指标预测值：

c.待预测日逐点误差预测。

采取平滑的方式得到待预测日误差预测标幺曲线。设平滑系数β，则待预测日的误差标幺曲线为：

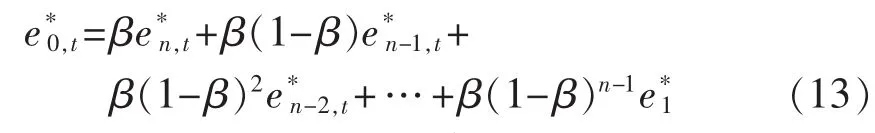
将标幺曲线有名化可得待预测日逐点误差e0，t=

经过上述过程就可以得到误差修正的最终预测结果：

3 算例研究

以某省夏季负荷为算例进行研究，所采用的历史样本为2013年8月1日至8月25日负荷数据及气象数据，对16日至25日10 d的负荷进行虚拟预测，每个虚拟预测日都对其基准日前两周的负荷数据进行频域分解。得到虚拟预测的误差进行建模后，对待预测日27日的负荷进行修正得到最后预测结果。以16日的虚拟预测为例，基准日前的两周1日至14日的频域分解结果如图2所示，图中横轴td值为0、1 表示第 1 天 00∶00、12∶00，2、3 表示第 2 天 00∶00、12∶00，其他依此类推。

可以看到日分量和周分量为强周期性时间序列，而低频分量和高频分量的剧烈波动也反映了该省夏季气象条件不稳定的特征。按照第2.1节中所述的算法求得10 d历史负荷虚拟预测的误差，其三维分布如图3所示。

图3显示误差分布是呈现相同趋势的一簇曲线，并在相同的时间出现峰谷值等。

在建立线性映射前需要首先对3种综合气象指标与误差分布的关系进行研究，以确定哪种综合指标对误差分布具有主导影响。计算虚拟预测10 d的实感温度、温湿指数和人体舒适度，分别与预测误差做拟合，其散点分布图4所示。

图2 频域分解结果Fig.2 Results of frequency-domain decomposition

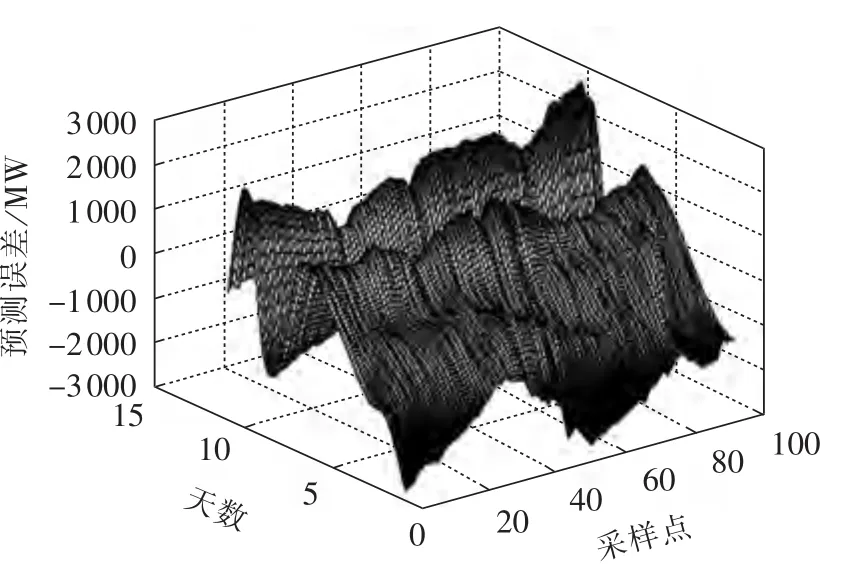
图3 虚拟预测误差分布三维图Fig.3 3D diagram of virtual forecasting deviation distribution

观察散点图发现，3种气象因素与误差基值的分布均有一定线性相关度。综合考虑各个影响因素提出的线性回归模型为：

其中，yi，1、yi，2、yi，3分别为历史第 i天的实感温度、温湿指数和人体舒适度3种综合气象指标。多元线性回归分析结果如表1所示。

图4 综合气象指标与误差散点图分布Fig.4 Scatter diagram of deviation distribution for comprehensive meteorological indexes

表1 多元线性回归分析结果Table1 Results of multivariate linear regression analysis

由表1可知，线性相关系数R2=0.8788，F统计量对应的概率P=0.0014＜0.05（显著性水平缺省值），可以用线性模型来建立误差与综合气象指标的之间的映射。可以看到温湿指数的拟合系数较大，证明了该省夏季的温湿指数是较为合理的综合气象指标。

获取待预测日的气象预报值 x0，1、x0，2、x0，3、x0，4，用第2.3节中的方式进行误差预测并得到误差修正后的预测结果。误差修正后的预测结果、未加修正的预测结果及实际负荷曲线的比较如图5所示。

图5 修正结果对比Fig.5 Comparison among real load，uncorrected forecasting and corrected forecasting

由图5可以看到，经过误差修正后的预测结果与实际负荷曲线的吻合度较高，尤其在峰谷段非常精确地符合实际用电规律，相比未加修正的预测结果精度有明显改善。其预测精度改善的根本原因为通过频域分解算法将气象对负荷的影响以误差的形式从原负荷中剥离处理，对气象因素以归纳为综合气象的方式与负荷进行了非线性相关建模，得到了高相关系数的误差修正模型。国家电力调度考核标准提供的日负荷精准率计算公式[12]如下：

其中，N为第i日负荷总点数；dit=（负荷预测值-负荷实际值）/负荷实际值×100%。根据准确率计算公式得到修正前后的准确率对比如表2所示。

表2 修正前后准确率对比Table 2 Comparison of accuracy between with and without correction

由上述结果可以看到8月16日负荷经过误差修正模型进行修正后的预测结果相比修正前提高了约6%，达到了非常高的预测精度。为了验证误差修正模型的预测效果，取考虑相关因素的预测模型中基于相似度计算的模式识别法和相似度外推法作为对照，按照本文的研究思路对2013年夏季6、7、8这3个月的负荷进行了算例研究，得到的各模型预测结果平均准确率对比如表3所示。

表3 多月平均预测准确率对比Table 3 Comparison of average forecasting accuracy for several months

表3显示经过误差修正模型的平均预测准确率具有明显的优势，相比模式识别法和相似度外推法准确率提高约2%～3%，在气象波动剧烈、预测精度普遍较低的夏季达到了约96%的预测精度，体现了该模型的优越性。

4 结论

本文通过对传统预测误差的分析论证表明传统预测方法的预测误差具有规律性，与特定的相关因素存在关联，可以与之建立映射。频域分解的预测误差主要由非周期分量的预测不准所致，非周期分量与气象因素具有较大关系。通过综合气象指标建立起单一气象指标的映射集合，与预测误差具有强线性相关关系，可以建立综合气象指标与预测误差的线性回归模型。最后以某省夏季负荷为例进行了算例验证，并跟目前常用的考虑相关因素的预测算法进行预测效果对比，预测精度平均提高了2%～3%，充分证明本文所提出的误差修正预测思路的正确性。

误差修正是负荷预测的一个新思路，因为预测误差往往蕴含着实际中某种因素的稳定影响，因此误差规律的研究是有价值的。对于自然气象条件不稳定的地区可以用支持向量机、神经网络或者模糊逻辑等方式进行非线性映射工具，结合本文所提出的线性回归模型可以构成完整的误差修正预测体系，提高预测精度。

同时，在实际应用中，误差修正的预测方法还存在依赖气象信息的准确性、复杂映射关系难以确定等缺点。本文提出误差修正是负荷预测的一个较新思路，有待进一步探讨和完善。