长江经济带高技术产业效率测度与异质性分析——基于三阶段DEA方法

谢洪军，张 慧

(重庆理工大学经济与贸易学院，重庆 400054)

一、引言

后金融危机时代，随着人口结构的转变、资源与环境约束趋紧，调整产业结构和转变经济发展方式成为我国的迫切任务。2014年12月的中央经济工作会议明确提出，经济“新常态”下应坚持以提高质量和效益为中心。这凸显出当前我国转变经济增长，注重发展质量的战略思想。技术效率能直观地反映产业效率和核心竞争力，是反映工业经济增长质量的重要指标之一。作为我国的动力型先导产业，高技术产业在中央及各地区工业经济中具有举足轻重的地位。长江经济带一直以来被誉为我国的“高科技走廊”，沿江地区高技术产业园区密集，在带动地区产业转型升级和地区经济腾飞中发挥着重要作用。然而，由于区域协调共生和产业联动机制尚未明确建立，各地区同质性发展和支柱性产业趋同问题日益凸现，其中高技术产业占据着重要地位。在此背景下，对长江经济带沿江省市高技术产业的技术效率进行合理评价，比较地区差异和行业差异，以此提出针对性的政策建议，对于探寻提高高技术产业的效率和质量的途径，优化长江经济带沿江高技术产业的资源配置和产业区域发展格局具有长远的现实意义。

对技术效率的测度，DEA和SFA两种方法使用最为广泛。国内外学者也较多采用这两种方法对高技术产业技术效率进行实证测度。Chung-Jen Chen 和 Chin-Chen Huang[1]、Min-Ren Yan 和 Kuo-Ming Chien[2]利用传统DEA模型基于台湾地区高科技工业园区数据分别对高技术产业和企业效率进行了评价。孙剑、李启明基于此模型对江苏省13市高技术产业企业的技术效率进行了测度[3]。DEA方法与因子分析方法的结合也已被一些学者所采用[4]。Subal Kumbhakar、Peter Voigt等采用随机前沿的SFA模型对欧洲高新技术企业2000—2005 年的效率进行了分析[5]。何维达等[6]、范凌钧等[7]、余泳泽等[8]同样采用此模型对我国整体及各地区高技术产业的效率进行了测度。鉴于DEA模型和SFA模型本身存在的局限和不足，Fried提出了三阶段DEA模型，这一方法对传统DEA方法进行了改进[9]，因而在近年高技术产业效率研究中被较多采用[10-12]。已有文献或基于全国层面或某一省份的高技术产业细分行业进行研究，或基于东中西部笼统的区域划分对高技术产业整体进行研究，但结合长江经济带和“高科技走廊”这一新的战略区域，基于地区和行业细分的视角，对沿江省市高技术产业效率进行合理评价，将更有针对性和参考价值。因此，本文基于沿江11省市2008—2013年数据，借助三阶段DEA模型，对长江经济带高技术产业效率进行更合理地评价，为沿江地区提高高技术产业各细分行业效率和发展质量，进而为政府决策提供依据和参考。

二、研究方法

DEA模型最早是由Charnes、Coopor和Rhodes于1978提出的。但是传统DEA测度方法将实际与前沿面的偏离全部归结为管理无效率因素，不尽合理。因此，Fried提出了三阶段DEA方法，剔除非管理因素对效率水平的影响，从而得到反映实际管理水平的效率值[9]。

(一)第一阶段:传统DEA模型

采用投入导向的BCC模型，在规模报酬可变的假定下评估决策单元的有效性。在BCC模型中，综合效率水平就被分解为纯技术效率和规模效率。传统DEA方法已较为成熟，此处对其线性规划原理不再赘述。

(二)第二阶段:类似SFA回归

第一阶段得出的投入松弛变量受到管理效率、环境因素和随机因素的影响，第二阶段通过构建类似SFA回归，对第一阶段中非有效决策单元的各项投入松弛进行分解，从中分离出环境变量和随机因素的影响。假设有n个决策单元和m种投入，构建SFA模型:

sij表示第j个决策单元的第i项投入的松弛变量，zj=(z1j，z2j，…，zpj)表示 p 个可观测的环境变量，β为待估计参数。fi(zj，βi)表示环境变量对投入松弛sij的影响，一般取线性形式。uij+vij表示混合误差，uij表示管理无效率因素，且假定其服从截断正态分布，即 uij～ N+(μi，)，vij表示产业噪音的随机误差因素，假定vij～N(0)，且 vij与 uij相互独立。定义，当γ越趋向于1，表明管理非有效因素作用越大，模型设定越合理。设γ=0和γ≠0的假设条件下待估计参数的极大似然函数值分别为 L(θ0)和L(θ1)，通过构建LR单边似然检验统计量，来检验模型设定的合理性。

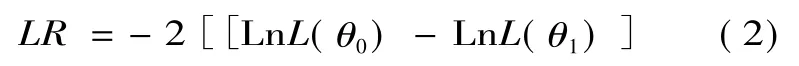
式(2)中，单边似然检验LR符合Mixed χ2分布，当LR大于其临界值时，拒绝γ=0的原假设，表明模型设定是合理的。根据回归结果，从中分离出环境变量和随机因素对投入松弛变量的影响，对决策单元的各项投入进行调整。根据Jondrow提出的方法，得到管理非效率的条件估计量[13]。

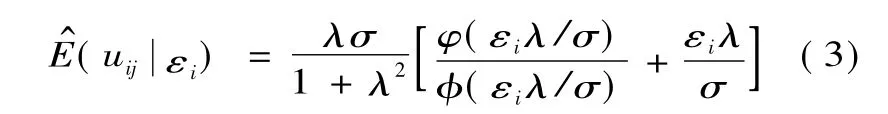
从中分离出环境特征和随机因素对投入松弛变量的影响，以最有效的决策单元为基准，对所有决策单元的各项投入进行调整

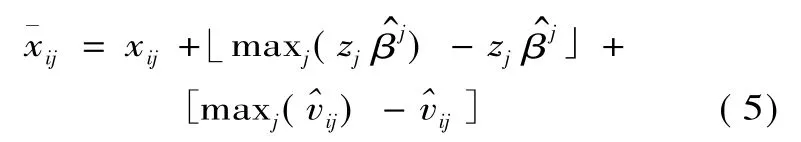
xij和分别表示调整前后的投入量，通过式(5)调整使得所有的决策单元面临相同的经营环境和运气。

(三)第三阶段:调整后DEA模型

将各决策单元经过第二阶段调整后的投入变量和原始产出变量，重新应用BCC模型进行效率测度，从而得到剔除环境变量和随机因素影响后各决策单元的效率值。

三、实证分析

根据《中国高技术产业统计年鉴》和《中国科技统计年鉴》中对高技术产业的分类标准，基于三阶段DEA评价模型，对长江经济带沿江11省市高技术产业五大细分行业的技术效率进行测度，包括医药制造业、航空航天器制造业、电子及通信设备制造业、电子计算机及办公设备制造业和医疗设备及仪器仪表制造业。研究的样本区间为2008—2013年6年的数据。数据来源于2009—2014年的《中国统计年鉴》《中国高技术产业统计年鉴》《中国科技统计年鉴》和《中国科技经费投入统计公报》。

(一)变量定义

1.投入产出变量定义

考虑到高技术产业的属性和发展特点，选取从业人员年平均人数(X1，人)、R＆D经费内部支出(X2，万元)和投资额(X3，亿元)三项投入指标。利润是反映产业现期生产运营能力和经济效益的直接指标，专利申请数排除了人为因素的影响，能够反映高技术产业的核心竞争力和未来产出增长潜力，因此选取利润总额(Y1，亿元)和专利申请数(Y2，件)两项作为产出指标。

投入产出指标的选取是应用DEA模型对产业效率进行科学合理评价的关键。本文的决策单元为11个，共选取3个投入指标和2个产出指标，满足模型要求。通过SPSS17.0软件对投入产出指标的相关性进行检验，利润总额与从业人员年均人数、R＆D经费内部支出、投资额的Pearson相关系数分别为 0.922、0.890、0.964，专利申请数与从业人员年均人数、R＆D经费内部支出、投资额的Pearson 相关系数分别为 0.969、0.942、0.899，且各系数检验均通过了1%的显著性水平，说明指标选取是合理的。

2.环境变量定义

在构建SFA回归模型中，考虑高技术产业的属性和发展特点，从宏观经济环境、产业竞争程度、科技活动环境和所有制结构4个方面考虑外部不可控因素:选取地区GDP作为宏观环境因素，选取产业企业数量衡量产业竞争程度，选取科技经费投入强度衡量科技活动环境。由于《中国高技术产业年鉴》从2012年起不再统计总产值和增加值指标，为统一口径，选取国有企业主营业务收入占行业主营业务总收入的比重作为所有制结构因素。

使用各省市历年GDP平减指数对地区GDP指标进行平减。由于没有经费支出、利润及投资额相关的价格指数，本文以2008年为基期，采用各省市历年的GDP平减指数对R＆D经费内部支出、投资额、利润总额三项指标进行平减，得到以2008年为基期不变价格的各项投入产出值。

(二)实证结果

1.第一阶段:传统DEA测度

不考虑环境条件和随机因素的影响，应用投入导向的传统DEA中BCC模型，对2008—2013年长江经济带沿江11省市高技术产业五大细分行业技术效率进行测度。由于云南省的航空航天器制造业和贵州省电子计算机及办公设备制造业数据缺失较多，故不做考察。应用Deap2.1软件对各省市五大行业2008—2013年技术效率测度并求均值，实证结果如表1所示。

表1 调整前各省市分行业5年技术效率均值

在不考虑环境特征和随机因素影响的情况下，就医药制造行业来看，上海和贵州6年均值处于技术效率前沿;云南、江苏、四川、重庆次之，6年效率均值均达到了0.9以上;江西和湖北技术效率水平均低于0.7，仍有较大的改进空间。对11省市6年效率求均值，医药制造行业6年综合技术效率为0.878，纯技术效率和规模效率分别为0.940、0.932，整体效率情况良好。

航空航天器制造业，安徽省处于技术效率前沿，纯技术效率和规模效率都达到最优。其次为重庆、浙江、江苏，效率均达到0.8以上。上海、湖南、湖北四省市技术效率均在0.6以下，其中湖北省最低，效率整体情况不理想。进一步分析发现，四省市低效率水平主要源自纯技术效率水平较低。

电子及通信设备制造业，贵州技术效率最高，处于效率前沿面。云南和浙江效率水平也相对较高，为0.9以上。其次为安徽、上海、江西。湖南在11省市中效率值最低，仅为0.694，其纯技术效率低于规模效率，成为综合效率的制约因素。

电子计算机及办公设备制造业，浙江处于效率前沿。四川、云南次之，均达到了0.95以上，两省市纯技术效率均达到了最优。湖南和江苏技术效率整体情况也相对较好。湖北和重庆相对效率水平最低，前者主要纯技术效率较低有待提高，后者是由于纯技术效率和规模效率均不高所致。

医疗设备及仪器仪表制造业，上海、浙江、湖南三省市处于效率前沿。四川和安徽次之，效率均达到0.95及以上。江西技术效率为0.541，远低于其他10省市。进一步发现其低效率水平源自纯技术效率较低，仍有较大的提升空间。

在不考虑环境条件和随机因素的条件下，长江经济带高技术产业中，医药制造业、电子及通信设备制造业和医疗设备及仪器仪表制造业综合技术效率分别为 0.878、0.832、0.869，纯技术效率和规模效率均远高于其他两行业。

2.第二阶段:类似SFA回归

为剔除环境变量和随机因素对技术效率的影响，第二阶段针对第一阶段中非有效决策单元，以各项投入变量冗余为被解释变量，以上文中构建的4个环境变量为解释变量进行回归分析。应用Frontier4.1软件，回归结果如表2所示。

3个投入松弛变量的回归模型中，大部分环境变量的参数都至少通过了10%显著性检验，γ均达到了0.999，表明管理无效率因素对各投入松弛变量产生了重要影响。且三个模型中LR单边检验均通过1%的显著性水平，表明构建类似SFA回归模型是合理且必要的。

3.第三阶段:调整后DEA测度结果

利用式(5)对所有决策单元的各项投入变量进行调整，对调整后的投入变量和原始产出变量重新应用投入导向的BCC模型进行效率测度，实证结果如表3所示。

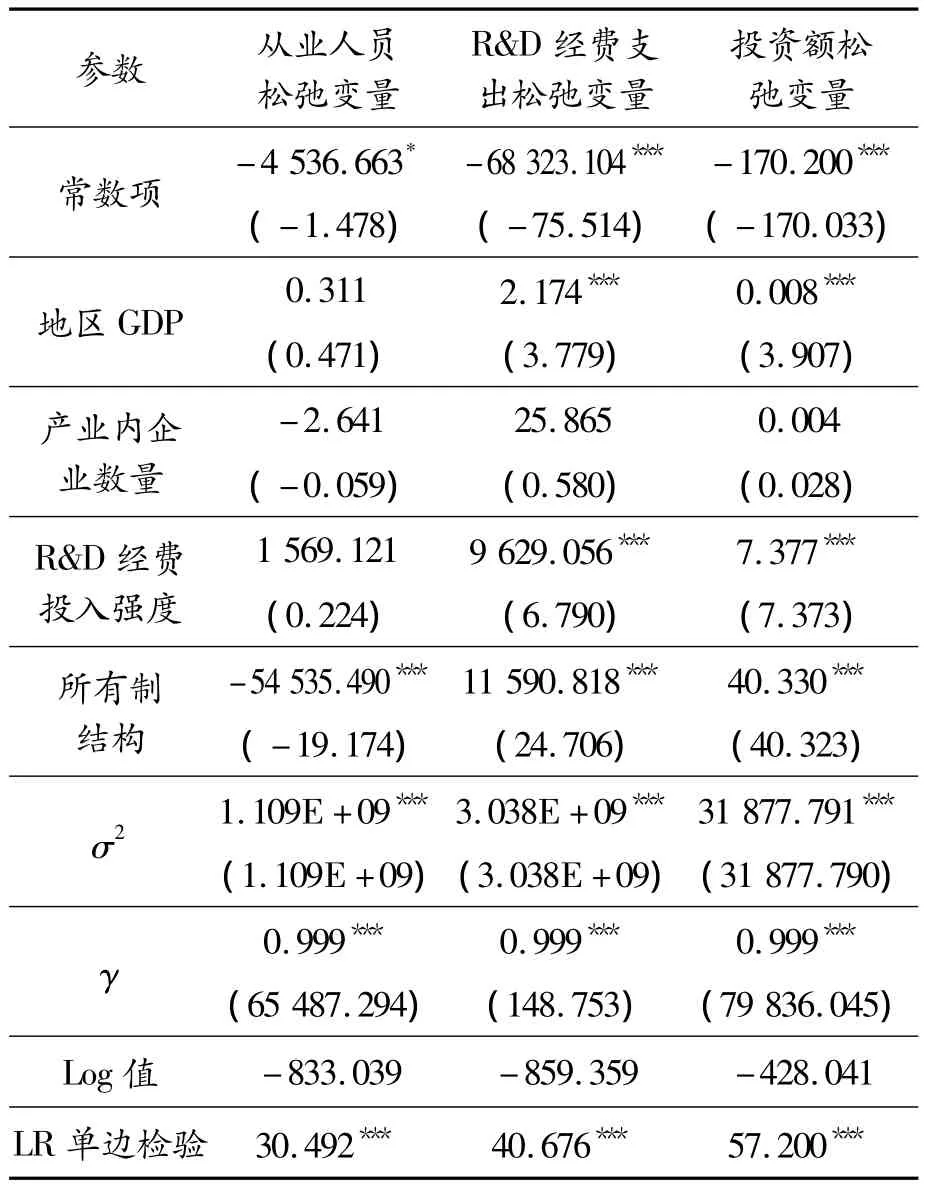
表2 类似SFA回归结果

表3 调整后各省市分行业五年技术效率均值

对比表1和表3剔除环境变量和随机因素的影响前后，各省市五大行业6年技术效率均值有明显改变，说明环境变量和随机因素会使技术效率评估出现偏差。调整后，医药制造业，上海和四川处于效率前沿;航空航天器制造业，江苏省处于效率前沿;电子及通信设备制造业，上海和浙江效率明显提高，与贵州一并处于前沿，江苏和四川效率水平也显著提高，云南、湖南和重庆明显降低;电子计算机及办公设备制造业，调整后浙江仍处于技术效率前沿，除了江苏效率提高外，大部分地区效率水平出现大幅下降，主要是调整后规模效率大幅下降所致;医疗设备及仪器仪表制造业，上海和浙江仍处于效率前沿，效率水平大多出现下降。

剔除环境和随机因素影响后，同质环境下11省市6年效率均值除医药制造和电子通信设备制造业综合技术效率水平有所提高外，其他行业效率均值均出现下降，进一步分析发现航空航天器制造业则源自规模效率水平的下降，其他两行业是由纯技术效率和规模效率共同下降所致。调整后效率的行业差异依然存在，医药制造业和电子及通信设备制造业效率水平较高，其他3个行业技术效率不尽理想。

四、结论与建议

本文应用三阶段DEA评价模型，对长江经济带沿江11省市高技术产业五大细分行业的技术效率进行实证测度，得出主要结论如下:

第一，沿江省市效率水平受到环境特征和随机因素的影响，剔除这些影响因素后，高技术产业各行业效率水平并不理想，仍有很大提升空间。调整后，除电子及通信设备制造业外，其他行业的综合技术效率均出现下降，技术效率水平较低。地区GDP、R＆D经费投入强度、国有企业占行业比重对R＆D经费支出和投资额两项投入冗余具有显著的正向作用，造成了资源的浪费，影响了产业效率水平。

第二，效率水平存在明显的行业差异和地区差异。从行业来看，医药制造业、医疗设备及仪器仪表制造业和电子及通信设备制造业3个行业的效率远高于其他两个行业，且剔除环境特征和随机因素影响后，差异仍存在。就地区来看，各地区5个行业的效率水平和优势产业也存在差异。

长江经济带一直以来被誉为我国的“高科技走廊”。然而实证结果表明，现有条件下，沿江高技术产业的实际产出并未达到最大化，效率水平并不理想，且存在较大的行业差异和地区差异。沿江省市应充分发挥特色资源和比较优势，有针对性地提高经营管理水平或规模收益，提高高技术产业的效率水平和发展质量。在“一带一路”国家战略实施的背景下，以高技术产业为支点，充分发挥高技术产业对其他产业的辐射和带动作用，促进人员、技术、资本等要素在长江经济带产业间的合理高效流动，有利于优化资源配置的区域结构和产业结构，形成优势互补、错位发展的竞争格局，避免下一轮粗放型增长和地区竞争中出现的低水平重复建设和产能过剩。

[1]CHEN C J，HUANG C C.A multiple criteria evaluation of High Tech industries for the science-based industrial park in Taiwan[J].Information ＆ Management，2004(7):839-851.

[2]YAN M R，CHIEN K M.Evaluating the Economic Performance of High-Technology Industry and Energy Efficiency:A Case Study of Science Parks in Taiwan[J].Energies，2013(2):973-987.

[3]孙剑，李启明.高新技术企业投入产出效率评价——基于江苏十三个城市的实证研究[J].科学学研究，2008(10):62-64.

[4]容美平，王斌会.我国各地区高技术产业投入产出效率综合评价[J].科技进步与对策，2010(7):26-28.

[5]KUMBHAKAR S C，LOVELL C.Stochastic Frontier Analysis[M].New York:Cambridge University Press，2000.

[6]何维达，张远德.基于非参数随机前沿面模型的高技术产业效率研究[J].经济经纬，2008(4):71-74.

[7]范凌钧，李南，陈燕儿.中国高技术产业技术效率区域差异的实证分析[J].系统工程，2011(2):57-62.

[8]余泳泽，张妍.我国高技术产业地区效率差异与全要素生产率增长率分解——基于三投入随机前沿生产函数分析[J].产业经济研究，2012(1):45-51.

[9]FRIED，LOVELL C，et al.Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis[J].Journal of Productivity Analysis，2002(17):121-136.

[10]王军，杨惠馨.2006—2008年中国省际高技术产业效率实证研究[J].统计研究，2010(12):47-49.

[11]吉生保，周小柯.基于三阶段DEA模型的中国高技术产业效率研究[J].中央财经大学学报，2010(12):62-66.

[12]张颖.基于三阶段DEA模型的安徽省高技术产业效率分析[D].合肥:安徽大学，2013.

[13]JONDROW J，LOVELL C A K，MATEROV I S.On The Estimination of Technical Inefficiency in the Stochastic Frontier Production Function Model[J].Journal of Econometrics，1982(19):233-238.