基于Harris-SIFT 特征匹配的图像自动配准算法研究

李玉峰，王竹筠

(沈阳航空航天大学 电子信息工程学院，辽宁 沈阳110136)

如今，图像配准成为在图像处理过程中很重要的一个环节，它是在不同的传感器、不同的时间段或者不同的视角下获取几幅图像进行匹配的一个过程。它的应用领域非常广泛，包括对医学图像、遥感图像的分析，以及在图像拼接、图像融合、目标识别，变化检测等图像处理过程中的应用［1－2］。目前，基于变换域、灰度信息和特征的匹配方法是最常用的方法［3－4］。其中，基于图像的特征是最为广泛应用的方法，它是寻找参考图像和配准图像之间共有的相似之处，通过两者在空间的位置关系来确定图像配准中的参数。首先对参考图像提取如拐角、点、线、边缘等具有不变特性的特征，然后在待配准图像中提取相似的特征来进行匹配。基于特征匹配方法速度快、精度高，在光照、变形、噪声等影响下，还是拥有良好的鲁棒性［5］。

基于特征的匹配方法是在两幅图像中寻找相同的特征，然后提取出来进行匹配，但要求这些特征具有稳定性。而基于特征点匹配的方法受到越来越广泛的重视［6］。目前广泛应用的点特征提取方法有:Harris 算子［7］、SIFT 算子［8］、PCASIFT［9］、ICA－SIFT［10］、SURF［11］算子等。SIFT(Scale－Invariant Feature Transform)算子是一种在尺度空间寻找特征的匹配算法，由David G.Lowe 在2004 年总结完善，它在不同尺度、光照发生变化、目标被遮挡及图像发生平移旋转时都仍具有较强的鲁棒性，因此在广泛应用于图像配准和目标识别等领域［8］。但由于SIFT 算法由于维数过大，提取特征点时间长，匹配存在错误等问题的存在，因此本文针对基于图像特征点匹配过程中，匹配精度不高、实时性不强的缺点，提出了通过结合Harris 和SIFT 算子对图像特征点进行提取与描述实现图像的高速和高精度的匹配算法。

1 图像特征点的提取与配准

图像配准一般分为4 个步骤:特征提取;特征匹配;变换模型参数估算;坐标变换与重采样。

1.1 特征点的提取

1)Harris 算子

Harris 算子是一种提取图像角点的算子它是在图像中，沿各个方向移动一个特定的小窗口，当这个窗口内的图像灰度发生明显变化时，那么就将窗口的中心像素点提取为角点。Harris 算子提取特征点的时间短、数量多，对于旋转图像，亮度、视角发生变化的图像都仍保持很好的鲁棒性［7］。

Harris 特征点检测数学形式为

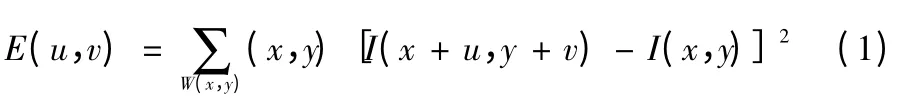
式中:E(u，v)表示在一个窗口中的平均偏移量函数;［I(x+u，y+v)－I(x，y)］2为图像灰度的梯度值;w(x，y)为加权函数。位移量(u，v)可用检测公式表示为

2×2 对称矩阵为

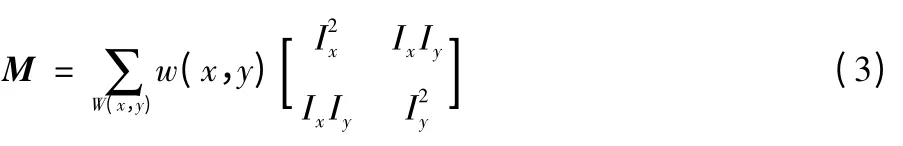
设λ1、λ2是矩阵M 的两个特征值，其中det(M)=λ1λ2，trace(M)=λ1+λ2。根据文献［7］所述，Harris 算子需要计算一个角点响应值R 来判断角点，R 计算如下

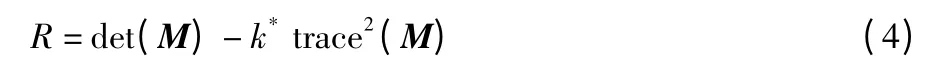
2)SIFT 算子特征描述

SIFT 是一种局部特征描述算子，在图像发生旋转、缩放以及尺度变化时都具有不变性，并且对目标遮挡、仿射变换和投影变换也有一定的鲁棒性。其基本思想是构建一个尺度空间，然后在此空间内寻找极值点，对极值点进行插值，从而找出稳定的特征点，为特征点建立一个描述符，通过描述符来对特征点进行描述［8］。

SIFT 算法对每个特征点都赋予了一个规范方向，先确定它们所在的局部位置，然后给它们赋予一个主方向。每个待确认的特征点可能会被赋予多个方向，但是最终只有一个主方向，当以特征点为中心，特征向量转为特征点主方向时，就具有了旋转不变性。计算公式为

式(5)是方向模值，式(6)是方向角大小。以特征点为中心，使用直方图统计其邻域内像素的梯度和方向。如图1 所示，图1b 为8 个主方向的梯度直方图，特征点的主方向由直方图的峰值来表示。此时已找到主方向的关键点就已经具有大小、尺度、方向信息。

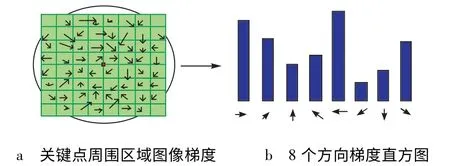
图1 绘制梯度直方图

接下来再对关键点进行描述，用一组向量将这个关键点描述出来，关键点以及其周围可以帮助描述关键点的像素点都是描述子，它会成为之后目标匹配的依据。对关键点周围的图像分成几个不同的区域，然后计算区域中每块的梯度直方图，从而生成在该区域中具有抽象性、唯一性的向量。Lowe实验结果表明，描述子采用以关键点为中心的邻域内4×4 的窗口，把360°分为8 个方向，通过绘制8 个方向的梯度直方图形成一个种子点，4 个种子点的信息来描述一个特征点。因此，当描述子采用128 维特征向量来描述特征点时，算法的整体效果可以达到最优［8］。如图2 所示。

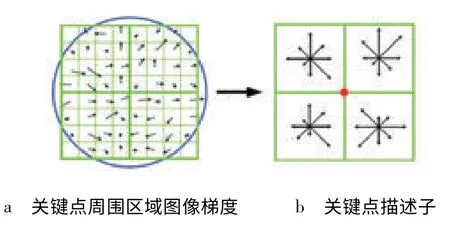
图2 特征描述子生成

1.2 特征向量匹配

特征匹配是通过特征描述算子及相似性度量来建立所提取的特征之间的对应关系。具有128 维的关键点描述子的相似性度量采用最近邻特征点距离与次近邻特征点距离之比进行匹配［12］。当参考图像中的每个关键点在配准图像中的最近距离与次近距离的比值在某一阈值内时，则认为是匹配点对［13］。

1.3 参数变换及重采样

在图像配准中，通常采用仿射变换来作为空间变换模型［14］。当在2 幅配准图像中确定了3 对以上的匹配点对之后，通过空间变换模型来求解参数，在确定了变换参数之后，需要对待配准图像进行重采样，以便把参考图像和带配准图像放在同一坐标系［15］。

2 改进后的图像配准算法

为实现图像的高精确与高效的配准，本文提出了一种基于Harris 检测算子和SIFT 描述子相结合的算法提取特征点，再利用欧氏距离和仿射变换模型来实现图像间的自动配准。实验结果表明，利用Harris 算子提取初始特征点可以节省SIFT 寻找极值点的时间，SIFT 算子也弥补了Harris 不具备的尺度不变性，两者相结合也增强了图像旋转、平移和仿射变换的鲁棒性，本算法不仅能实现图像特征点高精度的配准，还能减少提取特征点的时间，实现高效、高精度配准。算法流程图如图3 所示。

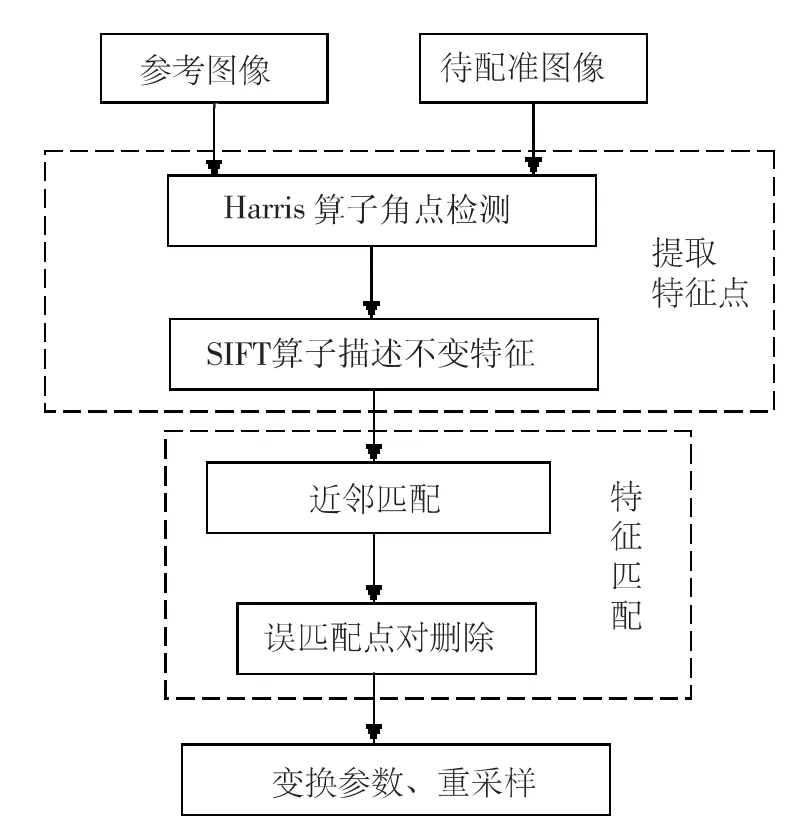
图3 改进算法流程图

首先，利用Harris 算法对图像提取出很多感兴趣的角点作为初始特征点，然后在提取出的初始角点基础上，本文利用SIFT 算法对这些初始角点进行特征描述从而得到新的特征点，经过筛选后的特征点即为本文所需要的最终特征点，它们将用在后面的图像特征点匹配中。在常用的SIFT 特征向量主方向的计算方法中，当特征点非常多的时候将会做大量的运算，工作效率较低。不同于SIFT 特征向量主方向的计算，本文特征向量的主方向选取为特征点在8 邻域灰度变化最大的方向。在图像中选取一个3×3 大小的模板，沿特征点的8邻域方向平移，分别记录每个方向下平移后模板内部灰度值的总和，再与该特征点处3×3 邻域内灰度值总和进行比较，找出差别最大时对应的方向，同时沿着这个方向，对图像进行旋转，使旋转后该方向与x 轴平行。当两幅具有重叠部分时，若图像进行刚性旋转，此方法均能保证旋转后图像保持一致，也就能保证特征向量的旋转不变性。与SIFT 描述子的主方向相比，本方法运算量大大减小，且同时能确保算法的准确性。找到主方向后，对两幅图像的特征点求其关键点的描述符，即特征向量，这里选择类似SIFT 描述符的生成方法。

图4 是以特征点为中心，取17×17 像素大小的邻域，在特征点的四个邻域方向外，我们可以把这些区域划分为16 个子区域，利用式(5)和式(6)计算每个区域的梯度方向直方图，在各个区域内描述出8 个方向，这样用来描述特征点的128 维特征向量就生成了。

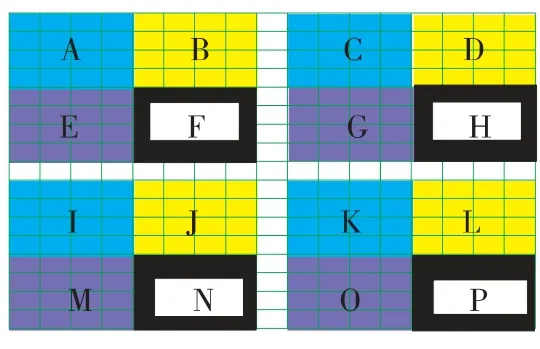
图4 128 维特征向量

当对两幅图像中的特征点进行匹配时，本文采用欧氏距离。通过计算待配准图像每个特征点到参考图像中的最近与次近的比值，当小于设定的阈值时，则认为这两个点为匹配点［12］。

3 实验结果与分析

本文为检测特征点的匹配精确度进行了100 对图像的匹配，下面选定四组图像进行实验。实验环境为Intel(R)2.6 GHz，内存为4.0 Gbyte，操作系统为Windows7，仿真平台为MATLAB R2008a。在Harris 算子提取角点的基础上，再利用改进的SIFT 算法对这些角点进行特征向量的描述，减少了经典SIFT 提取极值点的时间，最后求出满足设定阈值的点为匹配点。(本实验中，欧氏距离的阈值取0.6，Harris 算法参数k=0.04。)

3.1 图像配准实验

1)实验一

为了验证本文算法的可实行性和准确性，本文对图5、图6 两组大小为256×256 的参考图像进行旋转和平移，结果表明改进后的算法对旋转、平移均具有很好的鲁棒性。

图5 第一组实验图片

图6 第二组实验图片

2)实验二

实验图片选取为某海岸，图7a 图为参考图像;图7b 图为待配准的图像;图7c 图为Harris 算子提取的初始特征点图像;图7d 图是改进的SIFT 算法对图c 图这些初始特征点进行特征向量的描述，提取出新的特征点;图7e 为匹配图像;图7f 为根据仿射变换参数配准后的图像。

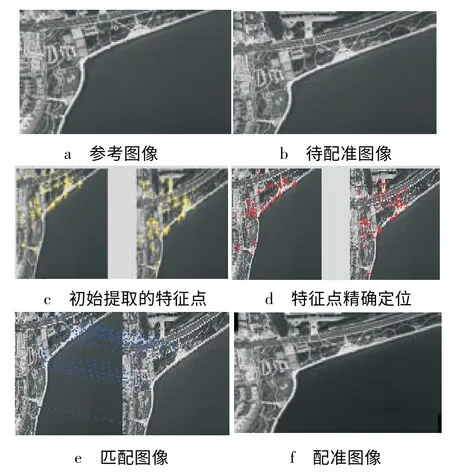
图7 第三组实验图片

图8 为另一组测试图片，实验图片选取在某湖泊。图8a、图8b 为参考和待配准的图像;图8c 图为改进算法匹配图像，图8d 图为根据仿射变换参数配准后的图像。

3.2 数据分析

1)特征点匹配情况分析

根据上述几例的结果图，统计匹配点是否正确匹配的情况如表1 所示。

图8 第四组实验图片

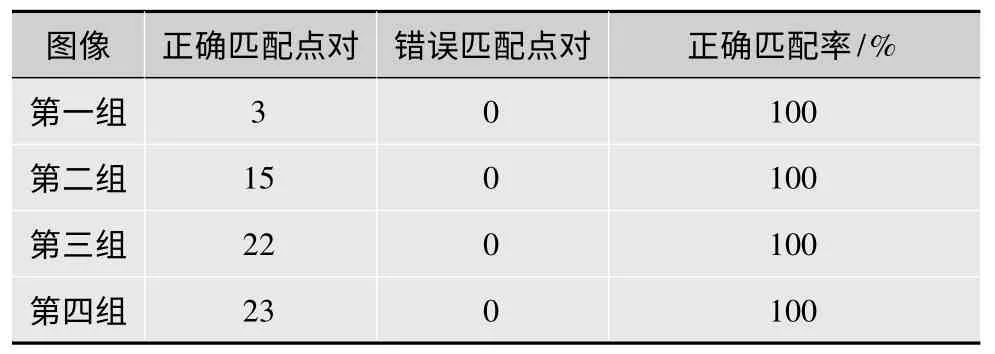
表1 图像匹配结果

由表1 可知，4 组图像没有误匹配点对。为验证本算法匹配的精确度，本文在200 幅图像的特征点匹配实验中，有5幅图像出现了特征点误匹配或没有可匹配特征点的情况，匹配率可达95%。大量实验证明，本文改进的算法具有高精确度的匹配性能。

2)算法时间效率的统计

为检测本文改进后的算法具有更好的实时性，本文对经典的SIFT 算法和改进的算法进行了对比，表2 列出几组数据供参考。

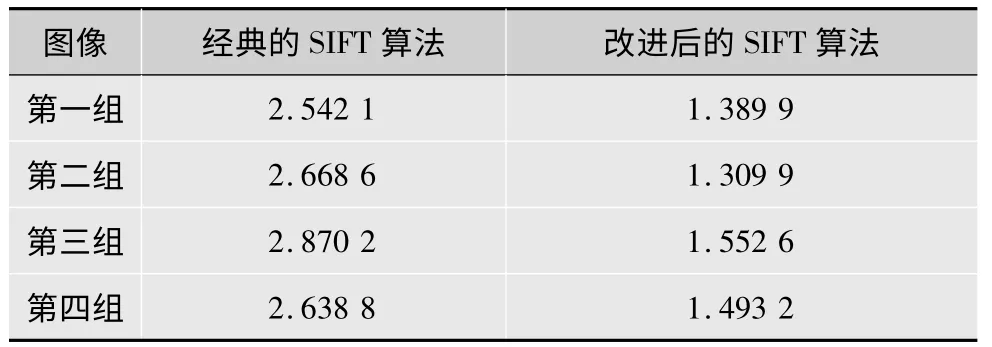
表2 本文算法与经典算法对比时间 s

由于篇幅原因，本文只列出4 组图像的数据，在对200 幅图像进行算法验证时，通过数据统计，经过改进后的SITT 算法同经典SIFT 算法相比，计算时间整体提高了47.51%。

从该结果图可以看出，由该河流的局部区域最终拼接出了该河流很大视野范围内的图像，两幅图片的边缘拼接处几乎没有缝隙，配准后的图片基本上实现了无缝融合，完全能满足观察和科学研究等需求。

4 小结

在本文中，作者详细描述了图像配准的具体流程以及配准中常用的三种方法，着重讲解了现在最为广泛应用的通过提取特征点来进行图像匹配的SIFT 算法。在此基础上，本文提出了一种对传统SIFT 算法改进的图像配准算法，它结合Harris 算法与SIFT 算法，在保留各自优点础上也互补了各自的不足点，本文对SIFT 算法求取主方向的复杂过程进行了合理的改进，不仅缩短了算法运行时间的，而且在图像配准的精度上也得到了提高。

［1］张锐娟.基于SURF 的图像配准方法研究［J］.红外与激光工程，2009，38(1):160－165.

［2］LIU Xiaojun，YANG Jie，SUN Jianwei，et al. Image registration approach based on SIFT［J］.Infrared and Laser Engineering，2008，37(1):156－160.

［3］曲天伟，安波.改进的RANSAC 算法在图像配准中的应用［J］.计算机应用，2010，30(7):1849－1852.

［4］王宏力，贾万波.图像匹配算法研究综［J］.计算机技术与应用，2008(6):17－19.

［5］CAO Jian，LI Kan. Application of local features in aerial image mosaic［J］.Journal of University of Electronic Science and Technology of China，2013，42(1):125－129.

［6］WANG Guicai，YU Junwei.An image registration algorithm based on features point and cluster［C］//Proc.International Congress on Image and Signal Processing(CISP 2012).［S.l.］:IEEE Press，2012:836－840.

［7］HARRIS C，STEPHENS M. A combined corner and edge detector［C］//Proc. Alvey Vision Conference 1988.［S.l.］:IEEE Press，1988:52－59.

［8］LOWE D G. Distinctive imgage features from scale－invariantkey point［J］.Interation Journal of Computer Vision，2004，60(2):91－110.

［9］KE Y，SUKTHANKA R.PCA－SIFT:AM or distinctive representation for local image descriptors［C］//Proc.International Conference Pattern Recognition.Washington，USA:［s.n.］，2004:36－39.

［10］DUAN C，MENG X.How to make local image features more efficient and distinctive［J］. IET Computer Vision，2008(2):178－189.

［11］BAY H，ESS A. Speeded－up Robust Features(SURF)［J］.Computer Vision and Image Understanding，2008(110):346－359.

［12］MIKOLAJCZYK K，SCHMID C. A perfomance evaluation of local descriptors［J］.IEEE Trans.Pattern AnaIysis and Machine IntelIigence，2005，27(10):1615－1630.

［13］刘辉，申海龙.一种基于改进SIFT 算法的图像配准方法［J］.微电子学与计算机，2014，31(1):38－42.

［14］LI Han，NIU Jizhen，GUO He. Automatic seamless image mosaic method based on feature points［J］.Computer Engineering and Design，2007，28(9):2083－2085.

［15］翟优，曾峦，王少轩.自适应对比度阈SIFT 算法研究［J］.计算机测量与控制，2011，19(11):2798－2806.