(MgC)n(n=1-10)团簇结构稳定性及金属性的第一性原理研究
2015-09-19吴学科
张 颂,岳 莉,吴学科,荆 涛,2
(1.凯里学院物理与电子工程学院,凯里556001;2.山东大学物理学院,济南250100)
1 引言
团簇是由原子、分子或离子通过物理或化学相互作用凝聚成材料的物质新层次,其性质不同于单个原子、分子或固体材料,而且不能利用单个原子、分子或固体材料的性质通过简单的线性外延或内插得到,这主要是因为团簇具有很强的量子效应和尺寸效应[1].基于这些奇特的效应,在其生长过程中,随着原子总数增加会出现一些极其稳定的尺寸,称为“幻数”结构.随着当前纳米材料微小化的不断发展,由“幻数”单元构成的纳米材料的开发、研究备受青睐.例如,以Pb7团簇为基元堆积生长而成的纳米材料具有超导性质,而Pb7刚好是中性铅团簇的“幻数”结构[2].另外,团簇在燃烧、光学、催化以及存储等领域存在极大的潜在应用价值,尤其是多元团簇,不同的结构、组分、掺杂的位置以及掺杂的元素等,都能将团簇的几何结构、电子结构,以及物理和化学性质进行广泛的拓展.因此,对多元团簇结构和性质进行比较系统的研究,在开发和设计低维纳米材料和纳米器械领域具有很高的价值.
众所周知,分别处于第二、四主族的Mg和C元素具有很奇特的性质和结构.对Mg团簇来说,随着尺寸的增加,其几何结构类似于金属团簇,但性质却发生显著的半导体性向金属性转变的行为[3].另外,掺杂的Mg团簇或固体材料不仅具有新奇的结构,还被认为是目前比较好的氢能储存媒介.例如,WilberSilva等采用密度泛函理论研究Ti掺杂Mg团簇的结构稳定性和储氢性能,以及Y.Bouhadda等利用第一性原理研究MgH2固体材料的储氢性能,都发现Mg的储氢性能比较好.最近FanjieKong等采用密度泛函理论研究了Fe,Co,Ni掺杂Mgn团簇的结构稳定性和磁性,发现Mg4X(X=Fe,Co,Ni)为该合金团簇的幻数结构[4-6].与 Mg团簇相比,C团簇显得更特别,C原子不仅能形成稳定的链状、管状、层状和足球状等结构[7,8],而且在微电子、光学器械和存储领域等都具有潜在的应用价值.于是,猜想如果将Mg和C两种原子进行有机结合形成团簇,是否能获得既不同于Mg团簇又不同于C团簇的稳定结构,以及此二元团簇是否还能保持纯Mg、C团簇的优越性质.虽然,PilarRedondo等[9,10]已采用理论计算方法对链状和环状MgCn,MgCn+和MgCn-(n=1-7)团簇进行比较系统的研究,发现偶数尺寸比奇数尺寸具有更高的稳定性,但至今还没有其它关于Mg和C二元团簇的研究.另外,通过改变二元团簇中原子的比例或位置,对寻找新型团簇结构、及其新的物理和化学性质意义重大.因此,镁、碳原子能形成何种团簇?结构演化中和性质变化中起决定性的因素是什么?以及镁、碳二元团簇是否具有比Mg、C团簇更优越的物理或化学性质都需要更系统、更深层次的研究.
综上,本文将采用基于密度泛函理论第一性原理,系统计算同比例镁、碳团簇(MgC)n(n=1-10)的结构稳定性及金属性,重点讨论其几何结构、电子结构、稳定性和金属性,寻找此二元团簇的“幻数”尺寸,并探索同比例二元团簇的性质随着尺寸变化的演化规律,为相关的实验做理论指导.
2 计算方法
本文利用广义梯度(GGA)近似下的BP(Perdew-Wangcorrelationfunctional)交换关联函数,所有计算都在Dmol3程序包中进行[11],结构优化中采用考虑相对论效应的全电子赝势,该势函数精度很高.为提高电子密度的精度,在使用多偶极矩拟合和双数值极化基组的基础上还选择八偶极机制和自旋非限制.此外,能量梯度、总能和原子位移的收敛精度分别为1×10-5eV/Å、1×10-6eV和5×10-4eV/Å.具体的计算过程中,当团簇总原子数N<8时,每尺寸几乎考虑到所有可能构型.然而,当N≥8时,由于初始构型非常多,不可能对每个结构都进行优化.于是,根据极小尺寸(MgC)n(n=1-7)团簇的成键行为和原子间的结合方式,首先考虑同主族元素单质团簇、电子结构相似的二元团簇的基态和亚稳态为候选对象,此后利用同比例碳、镁原子取代候选构型中的原子得MgnCn团簇初始构型并进行优化.其次,利用小尺寸同比例碳镁二元团簇基态构型进行堆积生长或在较小尺寸基态结构的不同位置添加原子来获得较大尺寸的初始构型.同时,由于某些情况下,高对称中电子态的简并会造成某些低对称性的构型比高对称性的结构还要稳定,因此,对同一尺寸初始构型,分别设置不同的对称性或限制对称性进行优化,这样能防止鞍点的出现及对称性对构型的影响.最后比较束缚能得(MgC)n(n=1-10)团簇的基态结构.
为验证该方法的可行性,于是利用 BP、PW91、PBE和BLYP交换关联势对Mg2、MgC和C2的键长、平均束缚能、振动频率和偶极矩进行计算,并将其与已有的研究进行比较 (表1).Mg2的键长、平均束缚能、振动频率BP计算值分别为:3.562Å,0.060eV,100.800cm-1,这与已有的研究 (3.580Å,0.049eV,97cm-1)吻合很好.同时,对于二聚体MgC,其键长和电偶极矩的BP计算值分别为:2.099Å,3.656Deby,与早期的研究结果 (2.066Å和3.5Deby)比较接近,虽然PW91的键长值 (2.095Å)更接近前期结果 (2.066Å),但其电偶极矩 (3.738Deby)偏差较大[9,12-15]. 因此,综合考虑发现采用BP交换关联势的计算值与已有研究结果吻合更好,说明本文所使用的计算方法是可行的,并期望可精确描述同比例碳、镁二元团簇的结构和性质.
3 结果与讨论
3.1 最低能量构型
本节重点讨论同比例碳、镁二元团簇(MgC)n(n=1-10)的结构特点,并将其与已有单质碳、镁团簇基态构型进行比较,探索经掺杂后(MgC)n(n=1-10)所展现出的较单质碳、镁团簇优越的稳定结构,并给出碳、镁二元团簇构型的演化规律.文中所有计算结果都列于表2中,虽然对每尺寸都优化很多结构,但是为简单化,在文中只给出最低能量构型(图1).
对于二聚体MgC,其最低能量结构的束缚能、键长和振动频率分别为0.996eV,2.099Å、512.2cm-1,是一个自旋单态,与 Mg2团簇(0.049eV,3.891Å 和 97cm-1)和 C2团簇(1.254 Å 和1940cm-1)稍有不同[9],与 Mg2相比发现,其束缚能高0.947eV,键长缩短1.792 Å,振动频率增加415.2cm-1,同时键长比C2高0.845Å,频率比C2低1427.8cm-1.显然Mg原子与C原子的结合,虽然能增加Mg团簇的稳定性,但又降低C团簇的稳定性,导致此现象的原因主要是Mg原子不能像C原子那样提供较多的价电子,这说明同比例碳、镁二元团簇可能具有较纯Mg、C团簇更优越的性质.
Mg2C2的最低能量结构与MgC相同,均为直线型,由图1知,该结构由两个MgC结构经碳原子相连接而成,其Mg-C和C-C键长分别为2.053Å和1.252Å,比二聚体 MgC的键长(2.099Å)稍短,但比已有研究中 C2的键长(1.245Å)稍长,说明碳、镁原子间的相互作用在增强[9,12,13]. 对 Mg3C3构型,初步优化时,除D3h、C3、C4v和C2v等高对称结构外,还考虑一些非对称的密堆积和松散构型,经优化后发现其最稳定结构类似于椅子,而且是平面形,3个碳原子连成一线,3个镁原子分居两侧.另外,Mg4C4的基态构型是由两个Mg2和两个C2间隔连在一起的高对称 (D2h)平面结构.从图1中可以看出Mg5C5和Mg6C6两团簇的基态结构既有显著的相同点,又有不同点,相同点是两构型中均含有Mg3C3结构,其中Mg5C5是由一个Mg3C3、一个Mg2和一个C2构成,而Mg6C6则是由两个Mg3C3连接而成,不同点是 Mg5C5是三维结构,而Mg6C6是平面结构,Mg5C5结构的突变主要来自于团簇物理学中的姜-泰勒效应.另外,以上的分析还可以说明Mg3C3为同比例碳镁二元团簇的“幻数”尺寸.

表1 采用BP、PW91、PBE和BLYP势函数对二聚体Mg2、MgC和C2的键长、束缚能、振动频率和偶极矩进行计算所得的值,并将其与已有的研究结果进行比较Table1 The bond lengths,binding energies,frequencies and dipole moments of2,MgCand C2are calculatedby BP,PW91,PBE and BLYP exchange - correlation functions,respectively,and compared with the previous research results
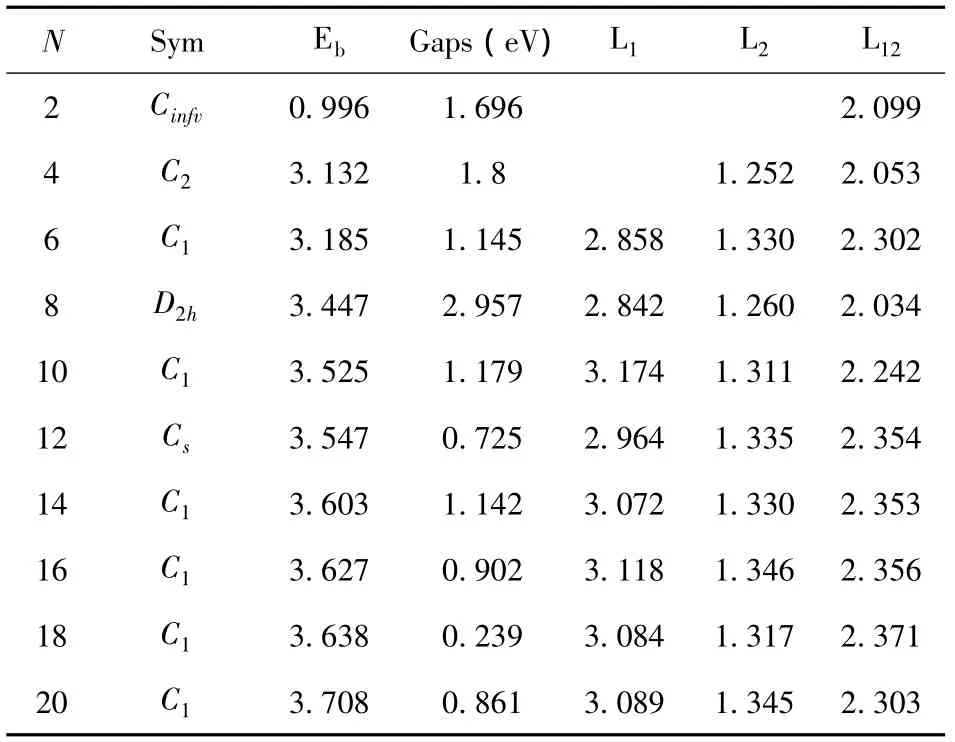
表2 团簇尺寸N,对称性(Sym),平均束缚能Eb(eV/atom),HOMO(最高占据轨道) -LUMO(最低未占据轨道)间的能隙Gaps(eV),Mg-Mg平均键长L1(Å),C-C平均键长L2(Å),Mg-C平均键长 L12(Å)Table2 The cluster sizes N,symmetries(Sym),bindin genergies Eb(eV/atom),Gaps(eV)between HOMO and LUMO,average bond lengths L1(Å)forMg-Mg,L2(Å)forC -CandL12(Å)forMg-C
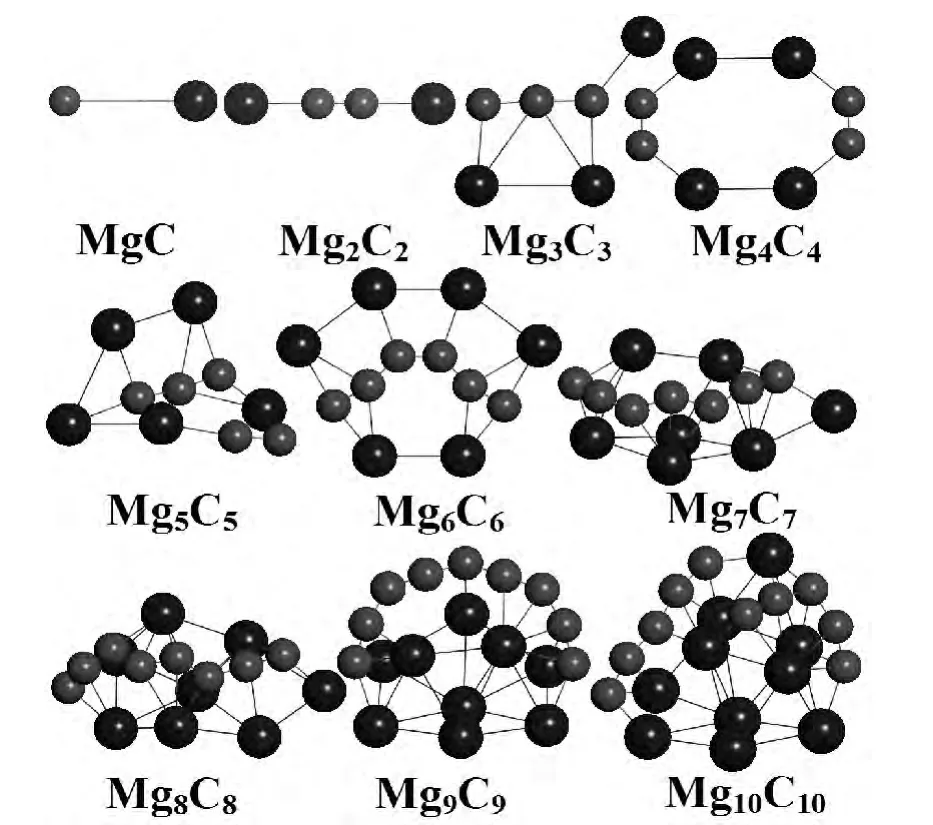
图1 (MgC)n(n=1~10)团簇的最低能量构型,其中Mg原子和C原子分别由蓝色大球和红色小球代表Fig.1 The low estener gystructures of(MgC)n(n=1-10)clusters,Mgand Cato msarere presentedby blueball and red ballres pectively
当总原子数大于12时,同比例碳镁二元团簇的最低能量结构都是三维构型,镁原子间表现出金属的密堆积形式,比较轻的碳原子则保持链状结构,且处于整个团簇构型的外表面形成奇特的结构.已有的研究显示,碳原子在形成团簇的过程中,当尺寸较小时稳定结构为链状[16],说明大尺寸二元团簇结构分别由两种元素各自团簇的键合.综上,碳镁二元团簇的结构不仅拥有碳、镁单质团簇各自的优点,还能形成奇特的构型.因此,若将此类团簇作为基元进行堆积生长的纳米材料可能会具有较单质碳、镁团簇材料更新的结构和性质.
3.2 结构稳定性
为进一步理解(MgC)n(n=1-10)二元团簇相对稳定性,定义团簇的平均束缚能为:Eb(MgC)n=[nE(Mg)+nE(C)-E(MgC)n]/(2n),其中E(Mg),E(C)和E(MgC)n分别为单原子镁、碳及二元团簇的总能.由图2知,当原子总数从2增加到4时,平均束缚能显著增加,但当N≥6时增加趋势变得缓慢.主要是在团簇的形成过程中,Mg和C原子的配位数都不能饱和,存在悬挂键.根据原子价电子Mg(3s2)和C(2s22p2)知,两元素的s轨道是填满的,但p轨道中电子占据极少,因此随着团簇尺寸的增大,原子的配位数由价态p轨道逐渐填满而增多,这使得团簇结构总能量降低,平均束缚能出现显著增大的现象.另外,当团簇总原子数超过6时,所有原子的配位数几乎达到饱和,对束缚能的贡献减小,平均束缚能变化平缓.已有的研究中指出,如此平缓的平均束缚能曲线说明,即使存在比所预测的团簇结构还要稳定的构型,其平均束缚能也不会比本文的基态结构偏离较多[17,18].因此,(MgC)n(n=1-10)二元团簇的稳定性决定于碳、镁原子之间的相互作用,例如,根据原子间化学键的数量和长度可以判断团簇的稳定性,数量多、长度短的化学键可以使团簇更加稳定.然而,如果需要寻找团簇的“幻数”结构,以及确定团簇间的相对稳定性,还需进一步研究平均束缚能的二阶差分(图2中插图),其定义为:Δ2E(MgC)n=E(MgC)n-1+E(MgC)n+1- 2E(MgC)n.
图2的插图中,二阶差分能量有3个峰值,分别对应于N=6、12和18,虽然后2个峰不很突出,但也能说明在所预测的团簇中N=6、12和18结构的相对稳定性最高,而且可认为N=6是二元团簇(MgC)n(n=1-10)“幻数”,这与结构分析中Mg3C3为团簇演化中的基本单元是吻合的.
团簇的平均键长反映原子间相互作用的强弱,可更深层次的解释团簇的稳定性,因此定义(MgC)n(n=1-10)团簇中原子间平均键长为:=(1/n)∑iRi,其中n是键长为Ri的个数,而Ri分别代表Mg-Mg,C-C和Mg-C在团簇中的键长,而L1(Å)、L2(Å)和 L12(Å)分别代表 Mg-Mg,C-C和Mg-C键长的平均值.图3中已经给出平均键长随团簇总原子数增加的演化曲线,除N=10外,3条曲线表现出几乎一致的变化趋势,说明文中所预测的稳定结构附近不会存在更稳定的结构,特别是在原子总数为10处Mg-Mg键长出现显著增强,这种结构参数的剧烈变化暗示该处结构将发生突变,这与最低能量构型分析中得到的结论一致.
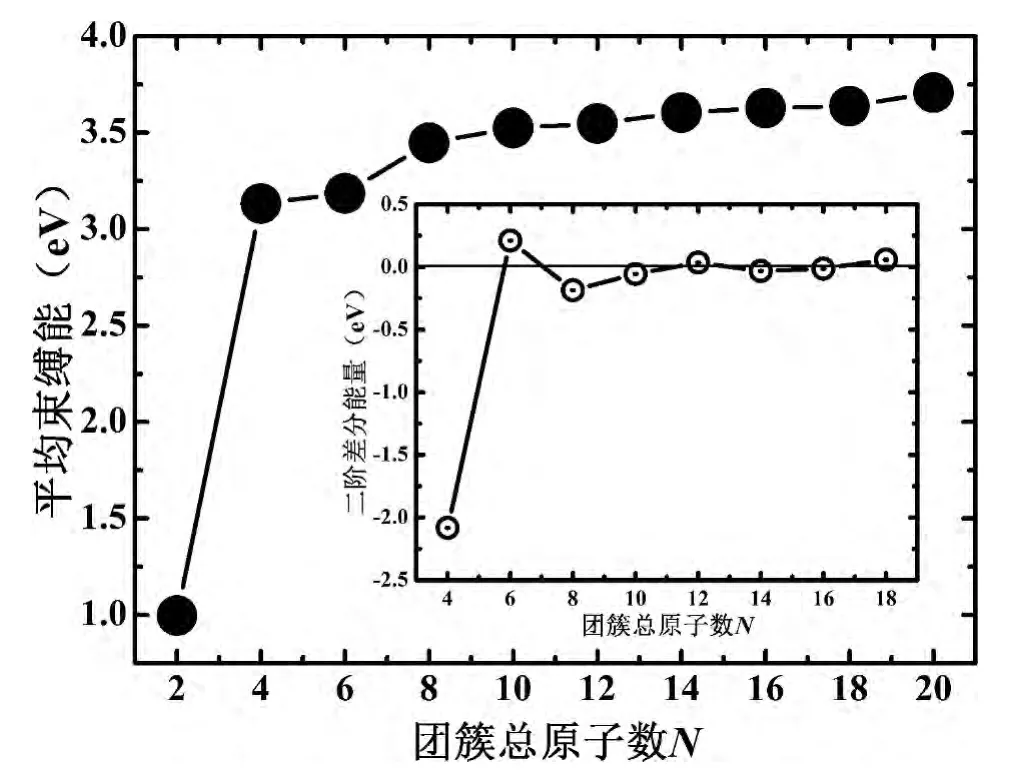
图2 (MgC)n(n=1-10)团簇的平均束缚能随尺寸的演化曲线,插图为(MgC)n(n=1-10)团簇的二阶差分能量随尺寸的演化规律Fig.2 The average bindingenergyasa function of the clustersizeN,andtheinset sho wsthe secon dorderdif ference of energies with respect tocluster sizeN
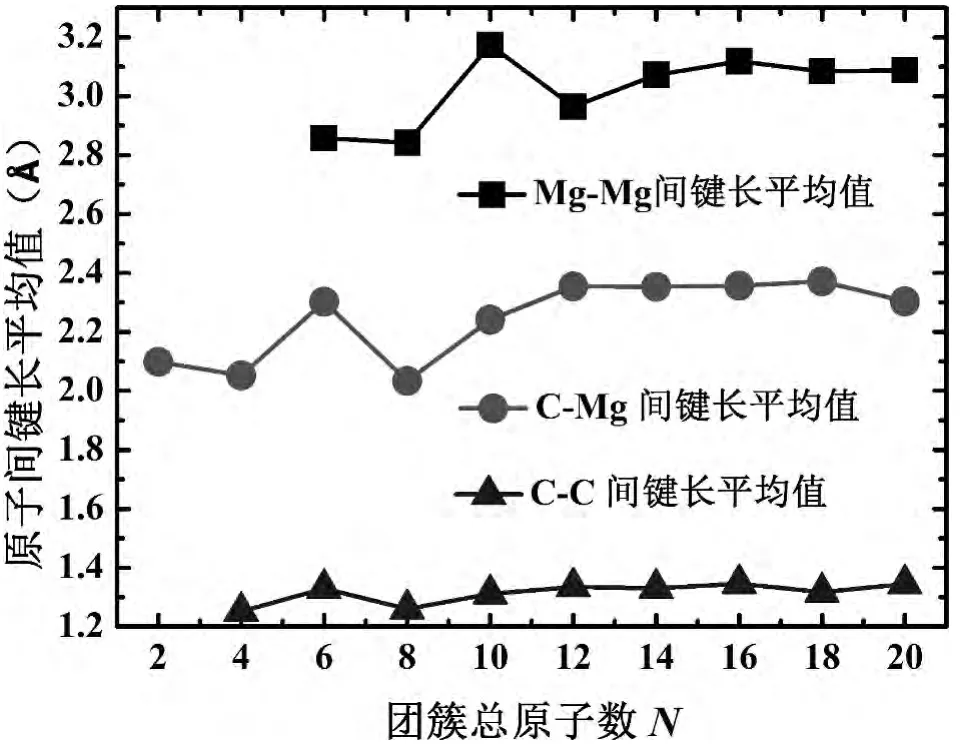
图3 (MgC)n(n=1-10)团簇中Mg-Mg、C-Mg及C-C原子间平均键长随着尺寸增加的演化规律Fig.3 The average bondlengthofMg-Mg,C-MgandC-Careplotte dagainsttoclustersize
3.3 金属性
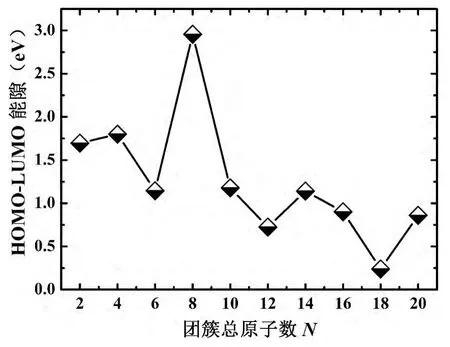
图4 (MgC)n(n=1-10)团簇的HOMO-LUMO能隙随尺寸增加的演化曲线Fig.4 Theevolution of Gap between HOMO-LUMOas function of clustersizein(MgC)n(n=1-10)clusters
从图4中看出,(MgC)n(n=1-10)二元团簇中,最高占据轨道与最低未占据轨道间的能量差值随尺寸的增加表现出比较奇特的振荡行为.随着原子总数N的增加,除N=8外能隙呈现显著降低的演化趋势,表示电子能从最高占据轨道跃迁到最低未占据轨道的概率越来越大,这说明随着尺寸的增加,同比例Mg、C团簇(MgC)n(n=1-10)发生范德瓦尔斯键向共价键或金属键转变的行为,这与纯镁团簇的研究类似[3].然而,在N=8处,能隙出现局域极大值,根据两元素的价电子Mg(3s2)和C(2s22p2)知,主要是由同比例碳、镁原子的闭壳层所致.
4 结论
本文采用第一性原理的方法对(MgC)n(n=1-10)二元团簇的结构稳定性和金属性进行系统的研究.得到以下结论:(1)同比例碳、镁二元团簇保持单质碳、镁团簇的基本构型,但表现出与纯团簇不同的结构和稳定性.在二元团簇形成的过程中,镁和碳原子首先形成各自比较倾向的结构后,再相互结合得奇特的结构.(2)(MgC)n(n=1-10)二元团簇的基态结构在原子总数N=10时发生突变:由平面形向三维结构转变.(3)最高占据轨道和最低未占据轨道间的能隙值除N=8外呈逐渐降低的趋势,说明在同比例二元团簇随尺寸增加的演化中出现半导体性与金属性间的相互转变行为.
[1]Wang GH.Cluster physics[M].Shanghai:Shanghai Scientific and Technical Publishers,2003:86(in Chinese)[王广厚.团簇物理学[M].上海:上海科学技术出版社,2003:86]
[2]Cuppens J,Romero C P,Van Bael M J. Superconductivity in Pb cluster assembled systems with different degrees of coagulation [J]. Phys. Rev. B,2010,81:064517.
[3]Thomas O C,Zheng W J,Xu S J,etal. Onset of metallic behavior in magnesium clusters [J]. Phys. Rev.Lett. ,2002,89: 213403
[4]Silva W,Truongb T N,Mondragon F. Electronic characterization and reactivity of bimetallic clusters of the Ti(Mg)ntype for hydrogen storage applications [J].J. Alloy. Compd. ,2011,509: 8501.
[5]Bouhadda Y,Rabehi A,Bezzari-Tahar - Chaouche S. First - principle calculation of MgH2and LiH for hydrogen storage [J]. Revue des Energies,2007,10:545.
[6]Kong FJ,Hu YF.Density functional theory study of smallX-doped Mgn(X=Fe,Co,Ni,n=1–9)bimetallic clusters:equilibriu mstru ctures,stabilities,electronic and magnet icproperties[J].J.Mol.Model.,2014,20:2087.
[7]Helden G V,Hsu M T,Bowers M T. Carbon cluster cations with up to 84 atoms: structures, formation mechanism,and reactivity [J]. J. Phys. Chem. ,1993,97: 8182.
[8]Tománek D,Schluter M A. Growth regimes of carbon clusters [J]. Phys. Rev. Lett. ,1991,67: 2331.
[9]Redondo P,Barrientos C,Cimas A,etal. Theoretical study ofMgCn,MgCn+,andMgCn-(n=1-7)open-chain clusters[J].J.Phys.Chem.A,2003,107:4676.
[10]RedondoP,Barrientos C,CimasA,etal.Theoretical study of smallMgCn,MgCn+,andMgCn-cyclic clusters[J].J.Phys.Chem.A,2003,107:6317.
[11]The DMol3 is a registered software product of Accelrys Inc.
[12]Raghavachari K. Structure,stability,and fragmentation of small carbon clusters [J]. J. Chern. Phys. ,1987,87: 2191.
[13]Teberekidis V I,Kerkines I S K,Tsipis C A. Ground states of BeC and MgC: a comparative multireference brillouin – wigner coupled cluster and configuration interaction study [J]. Int. J. Quantum Chem. ,2005,102: 762.
[14]Köhn A,F Weigend,R Ahlrichs. Theoretical study on clusters of magnesium [J]. Phys. Chem. Chem.Phys. ,2001,3: 711.
[15]Martin J M L,Taylor P R. Structure and vibrations of small carbon clusters from coupled - cluster calculations [J]. J. Phys. Chem. ,1996,100: 6047.
[16]Raghavachari K,Binkley J S. Structure,stability,and fragmentation of small carbon clusters [J]. J. Chem.Phys. ,1987,87: 2191.
[17]ZhangS,YueL,WuB.The structural stability and metallicity of(PbSn)n(n=1 -10)alloyclusters[J].J.At.Mol.Phys.,2013,30:396(inChinese)[张颂,岳莉,吴波.(PbSn)n(n=1-10)合金团簇的结构稳定性及金属性的研究[J].原子与分子物理学报,2013,30:396]
[18]YangXD,WuB,ZhangS.The structural stability and metallicity of PbnSn(n=1-19)alloyclusters[J].J.At.Mol.Phys.,2012,29:445(inChinese)[杨秀德,吴波,张颂.PbnSn(n=1-19)合金团簇的结构稳定性及金属性的研究[J].原子与分子物理学报,2012,29:445]
