密度泛函理论研究KBn(n=1-9)团簇的结构和性质
2015-09-19孙凌涛郭朝中石东平
孙凌涛,郭朝中,石东平
(重庆文理学院新材料技术研究院,重庆402160)
1 引言
团簇因具有独特的物理化学性质和潜在的应用价值,一直引起人们广泛的研究兴趣.近年来,研究发现硼化物一般都具有耐高温、耐腐蚀和抗氧化等优点,在光电子等领域有着广泛的应用前景.B是最轻的三价主族元素,有着2s22p1的价电子层结构,易于形成sp2杂化,人们对于掺杂硼团簇[1-5]有着较多的研究 . 实验方面,Chopra等人[6]以及 Lee等人[7]已经在实验上合成了硼氮纳米颗粒.Hanley及其合作者[8]已经通过分子束外延技术和激光烧蚀技术合成了硼团簇,并通过飞行时间质谱技术研究了它的性质,预言纯硼团簇是三维结构.理论方面的报道也很多,Niu等人[9]研究了BNX(X=C或Be)团簇的基态结构及其稳定性.杨志及其合作者[10]利用密度泛函理论中的广义梯度近似(GGA),在考虑自旋多重度后,对FeBN(N≤6)团簇基态结构、电子性质进行了探讨,结果发现在N=4时团簇的磁矩就发生了猝灭现象,团簇的总磁矩和平均磁矩随B原子数的增加而出现振荡.最近研究表明碱金属硼氢络合物具有很好的储氢能力、由碱金属硼和氢元素组成的配位金属氢化物将有望成为未来最有发展潜力的新型材料之一[11,12],据我们所知,对碱金属掺杂硼团簇的研究已有一些报道[13,14],人们一直希望从理论层面揭示出碱金属掺杂硼团簇的形成机理,因而研究碱金属掺杂硼团簇是一件很有意义的工作.如阮文及其合作者[15]研究了NaBn(n=1-9)团簇的几何结构和电子性质 .Li等[16,17],研究了MB5(M=Li,Na,K,Rb,Cs)和 MB7(M=Li,Na,K,Rb,Cs)体系的基态几何结构和电子性质等. 赵等人[18],对MB10(M=Li,Na,K)团簇体系的几何结构和振动频率进行了探讨,然而对K掺入Bn团簇的理论研究至今报道还很少.本文对KBn(n=1-9)团簇进行了系统的理论研究,得到了基态结构,其结论将为对该体系感兴趣的实验工作者对于理解小尺寸团簇的形成机理、稳定性规律及寻找更大尺寸团簇的形成机理提供有意义的参考价值,为以硼团簇为基元合成具有特殊功能的新材料提供理论依据.
2 计算方法
利用DMol3程序包中自旋极化密度泛函理论进行结构优化.计算过程中选择广义梯度近似(GGA)、Becke-Lee-Yang-Parr关联修正、带极化的双数值原子基组(DNP)和自旋非限制近似(SCF)求解自洽场.几何结构优化过程中位移量收敛标准取0.050nm,原子间作用力收敛标准取0.020Hartree/nm,能量收敛标准取2×10-5Hartree.自洽场收敛标准取10-6Hartree,该模拟条件研究团簇的有效性在先前研究中得到了验证[19].
对于对于KBn(n=1-9)团簇,随着B原子数的增加,仅从几何角度来考虑,其可能的初始结构、各组分团簇的同分异构体会很多.为有效地找出体系的稳定结构,我们对于确定尺寸的团簇,尽可能多的设计各种可能构型,分别在不同的自旋多重度下进行结构优化、能量和频率等性质的计算.在设计团簇初始构型时,参考前人对纯硼团簇的几何构型,初始构型中原子间距参考纯硼块体原子间距.给定初始构型后,采取替换、带帽的结构探索法,对K原子处于不同位置分别进行优化,这样原先的一个初始构型就变成若干个几何构型,虽然计算工作量增大,但保证了结果的可靠性.最后选出能量最低且无虚频的结构为该团簇的基态结构.
为了对所用计算方法进行标定,我们在相同的条件下计算了B2二聚体的键长、振动频率和平均结合能等物理量.计算结果表明:自旋五重态且能量较低的B2键长值为0.1620nm,振动频率为998.80cm-1与理论计算值(键长为0.1617nm,振动频率为 1004.50cm-1)[20]和实验结果(键长为0.1590nm,振动频率为1051.30cm-1)[21]符合很好,这很好的说明了我们所选用的方法是合适的.
3 结果与讨论
3.1 KBn(n=1-9)团簇的稳定结构
以总能量为判据,能量越低越的结构稳定性强,且以结合能为辅助参考,确定出了KBn(n=1-9)团簇的最稳定构型(带星号的)及其部分能量最低的亚稳态构型,如图1所示.KBn(n=1-9)基态团簇,随着B原子数目的增加,团簇的结构从一维到二纬再到空间三维的逐级转化,结构越来越复杂,同分异构体团簇也越来越多.1a是一字型的线状结构,B原子和K原子分布在线状结构的两端,B-K原子间的键长为0.162nm.随着B原子数增加一个的2a,是个对称性为C2v的等腰三角形结构,可以看作是一个B原子吸附到了1a结构上而得到,三角形结构腰和底边的长度分别为2.874nm、1.621nm,三角形的顶角和底角角度分别为34.82度和72.59度.对称性为C2v的3a是一面状的四边形结构,分布在四边形顶端的K原子和其对角的B原子构成了此结构的对称轴,对称轴两端为全等的两三角形,此对称轴上的K-B原子间的距离为2.684nm,K原子所在顶角的度数为68.951度.具有C1对称性的4b其结构可以看作是一个K原子吸附在了一纯B3团簇一侧边上而得到.KB5的基态结构5a是一不规则的单锥结构,中心B原子拉伸出整个结构形成锥顶,具有Cs对称性.KB6的基态结构6a是一不规则的车轴型结构,K原子吸附于纯B6团簇的结构上,具有C2v对称性.7a是一拉伸较长的C6v帽状结构,K原子吸附于帽状结构的顶端,KB7的基态结构较其亚稳态结构结合能低0.0599eV.8a是一畸变的舵盘结构,K原子吸附于舵盘结构的一个顶点上,K原子与盘心得B原子间的键长为4.411nm,具有C2v的对称性.KB9的基态结构,是具有C8v对称性的轮盘上吸附一K原子的带单准的结构,K原子与轮盘中心B原子间距为2.918nm.
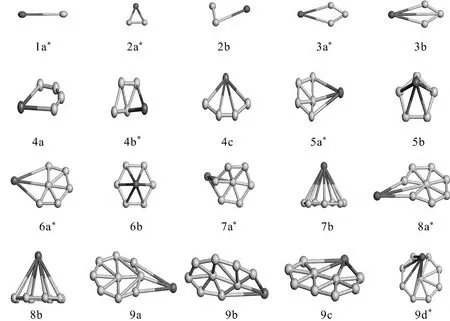
图1 KBn(n=1-9)团簇的稳定结构(浅色的代表B),带星号的为KBn(n=1-9)团簇的基态结构Fig.1 The possible geometry structures ofKBn(n=1-9)clusters
3.2 KBn(n=1-9)团簇的稳定性
为了研究KBn(n=1-9)团簇的稳定性,我们对KBn(n=1-9)团簇基态结构的平均结合能Eb、劈裂能D(n,n-1)和能量二阶差分△2E进行了计算.计算公式如下:
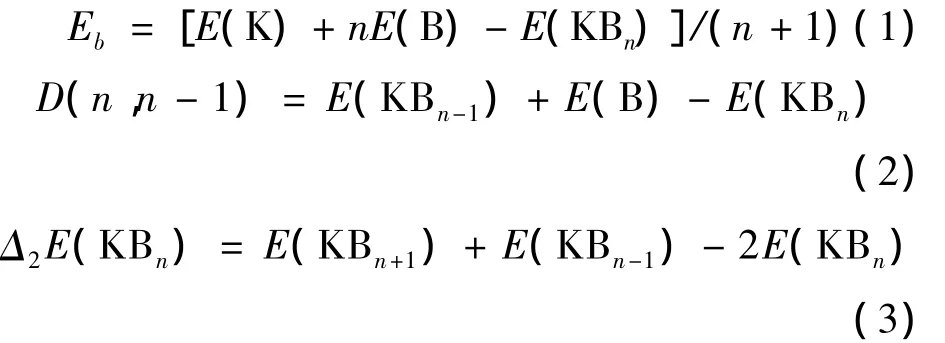
其中(1)、(2)和(3)式中n表示KBn(n=1-9)团簇中B的变化数,(1)式中E(B)、E(K)、E(KBn)分别表示B、K、KBn团簇最稳定结构的总能量.平均结合能越大,分子越难被分解成单个的粒子,平均结合能是反映团簇的稳定性很好的物理量.(2)、(3)式表示的是Si原子数目随n变化时KBn(n=1-9)团簇的劈裂能、能量二阶差分值变化值,劈裂能D(n,n-1)和能量二阶差分△2E从另一个侧面描述了团簇稳定性.
为了比较掺入K原子对Bn团簇稳定性的影响,我们使用了文献 [22]中Bn(n=2-10)团簇的平均结合能数据.Bn团簇和KBn团簇的平均结合能随团簇尺寸变化的曲线如图2所示.KBn团簇的平均结合能明显高于Bn团簇的,表明K原子的掺入增强了主团簇Bn的稳定性,由此可知掺杂B原子是很有意义的.对于KBn(n=1-9)团簇,尺寸在n=1-3范围内,团簇的平均结合能增长的非常迅速;尺寸在3-9范围内,虽然平均结合能仍不断增大,但增长速度有所减缓;总体来说,随着团簇总原子数的增加,KBn(n=1-9)团簇的平均结合能逐渐增大,说明团簇的稳定性逐渐增强,平均结合能最高的是KB9团簇,团簇中所含B原子数最多,其稳定性最高.
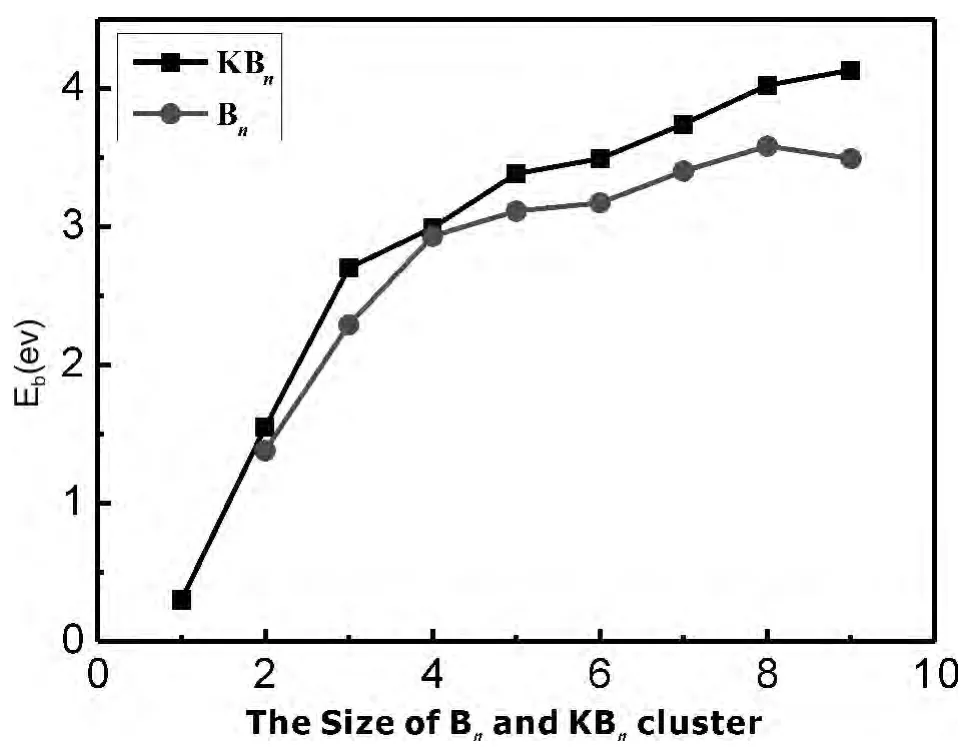
图2 Bn和KBn团簇不同尺寸的平均结合能Fig.2 Size dependence of the atomic averaged binding energies(Eb)of theBnand KBnclusters
图3 是KBn(n=1-9)团簇能量二阶差分△2E和劈裂能D(n,n-1)随团簇尺寸变化的关系图,对△2E和D(n,n-1)来说,其峰值表示对应尺寸的团簇比相邻尺寸的团簇要稳定.从图3可知,随着尺寸的增大,二阶能量差分△2E呈现出波动性,n=3、5时出现峰值,表明KB3和KB5团簇较相邻团簇在结构上更稳定.KBn(n=1-9)团簇的劈裂能曲线也呈振荡变化,并且在n=3、5时与相邻尺寸团簇相比出现最大值.综合二阶能量差分和劈裂能可以得出:KB3和KB5为幻数团簇.
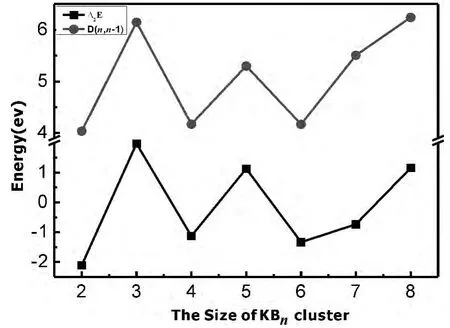
图3 KBn团簇不同尺寸的△2E和D(n,n-1)Fig.3 Size dependence of the fragmentation energies and the second order differences of theKBnclusters
3.3 KBn(n=1-9)团簇的能隙
图4 给出了KBn(n=1-9)基态团簇的能隙(Gap)随团簇总原子数的变换关系,能隙在固态物理学中指半导体或绝缘体价带顶端至传导带底端的能量差距.其物理意义上:HOMO能级反应了失去电子能力的强弱.相对的,LUMO能级反应了获得电子能力的强弱,而能隙则反映了电子从最高占据分子轨道(HOMO)向最低未占据轨道(LUMO)发生跃迁的能力,在一定程度反应了分子参与化学反应的能力.
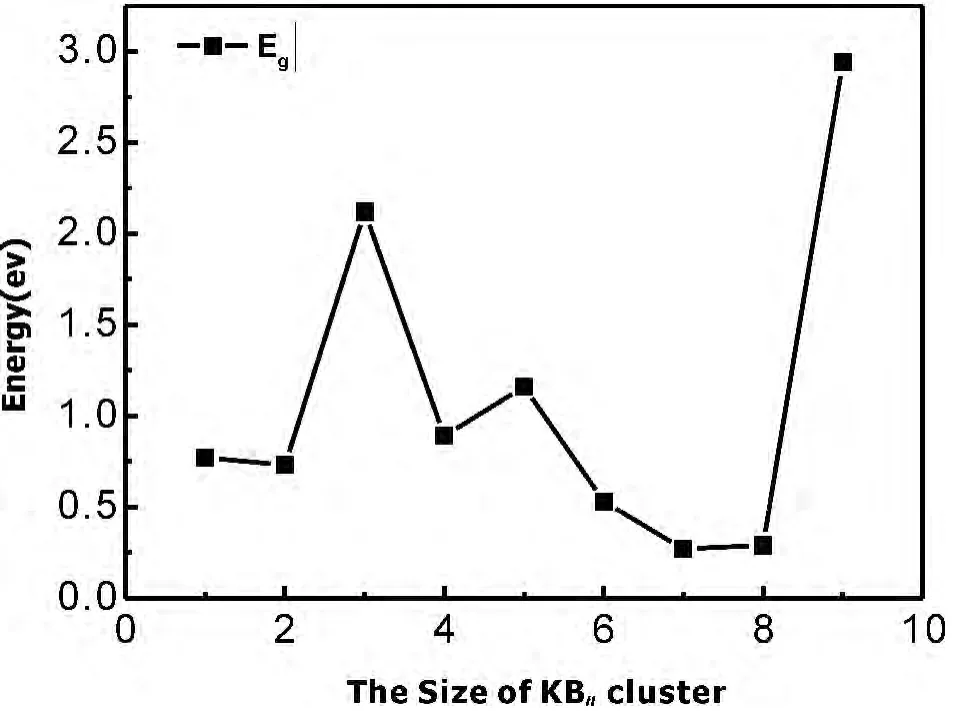
图4 KBn团簇不同尺寸的能隙EgFig.4 Size dependence of the HOMO-LUMO energygap of theKBnclusters
从图4可以发现:能隙随着团簇总原子数的增加呈振荡变化,且n=3、5和9时出现相对较高的峰值,说明KB3、KB5和KB9团簇较其它团簇稳定性要高,这和KBn(n=1-9)团簇能量二阶差分△2E和劈裂能D(n,n-1)随团簇尺寸变化的关系所得:KB3和KB5为幻数团簇,取得了很好的一致.图4中能隙最大的是KB9团簇,其值为2.94eV.其次KB3团簇具有2.12eV的能隙值,KB7团簇具有最小的能隙值0.27eV,整个能隙带表现出了半导体和金属的多重性质.由能隙图,总体来说:KB9团簇的化学活性最弱,KB5团簇的化学活性最强.
3.4 态密度分析
为了对图4中KBn(n=1-9)团簇能隙振荡变化原因作讨论,我们选取了KBn(n=1-9)基态团簇中KB7、KB9的总态密度和分布态密度来进行对比研究.
图5、6中,Fermi能级已移到零点,可以看出:K原子掺入后,使KB7、KB9团簇的价带带宽增长.KB7团簇在离费米面-0.5782Ha处K原子的p轨道贡献一峰值,同样的KB9团簇在离费米面-0.5344Ha处出现由K原子p轨道提供的一峰值,这说明K原子的掺入使得团簇稳定性增强,这和图二中Bn团簇和KBn团簇的平均结合能对比结论取得了很好的一致.从KB7和KB9团簇态密度图的导带和价带之间的带隙来看,KB7团簇的带隙远小于KB9团簇,说明KB7团簇价带的电子更容易通过禁带达到导带,表现出较为活泼的化学性质,从而说明了能隙振荡变化的具体原因.
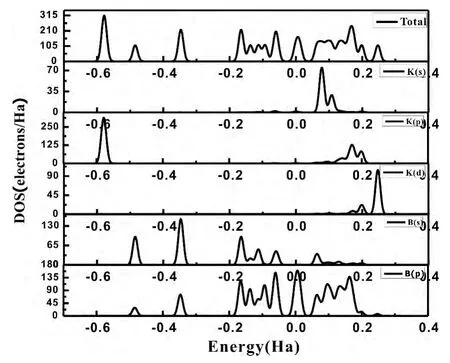
图5 KB7团簇的的电子总态密度和分布态密度Fig.5 Total density of states ( TDOS) and partial density of states ( PDOS) of clusterKB7
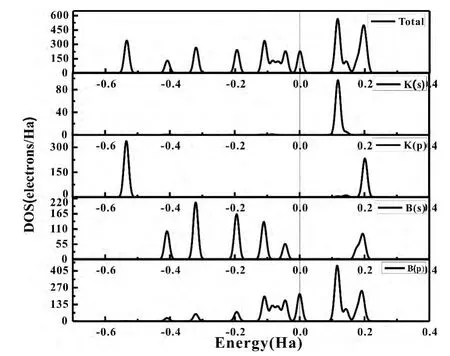
图6 KB9团簇的的电子总态密度和分布态密度Fig.6 Total density of states ( TDOS) and partial density of states ( PDOS) of clusterKB9
4 结论
采用密度泛函理论研究了KBn(n=1-9)团簇的可能结构、基态结构相对稳定性、及其随团簇尺寸变化的趋势,对KBn(n=1-9)团簇数据对比分析,具体结论如下:
(1)KBn(n=1-9)团簇,随着团簇尺寸的变化,其平均结合能都逐渐增大,即其稳定性逐渐增强.
(2)随着团簇尺寸的增加,KBn(n=1-9)团簇的能量二阶差分△2E、劈裂能D(n,n-1)呈现振荡变化,其中n=3、5时与相邻尺寸团簇相比都出现峰值,说明KB3和KB5为幻数团簇.
(3)KBn(n=1-9)团簇能隙结果表明:能隙随着团簇总原子数的增加呈现振荡变化,通过对比分析KB7、KB9团簇的态密度,表明造成能隙振荡变化的原因是由于团簇带隙的差异.
[1]Hayami W. Theoretical study of the stability of12(A=H - Ne)icosahedral clusters[J].Phys.Rew.B,1999,60(3):1523.
[2]La Placa S J,Roland P A,Wynne J J. Boron clusters(Bn,n=2-52)produced by laser ablation of hexagonalboron nitride[J].Chem.Phys.Lett.,1992,190(3-4):163.
[3]Atis M,Ozdogan C,Guvenc Z B. Structure and energeticof Bn(n=2-12)clusters:Electronic structure calculations[J].Int.J.Quantum Chem.,2007,107(3):729.
[4]Zhang WQ,Zhang XF,GaoYH,etal.Structure and magnet ism of MnBn(n=1 - 7)clusters[J].J.Magn.Mater.Devices,2009,40(4):15(inChinese)[张文庆,张先富,高银浩,等.MnBn(n=1-7)团簇的结构和磁性[J].磁性材料及器件,2009,40(4):15]
[5]ZhaoYF,TianK.Density functional theory study of MgBn(n=1 - 17)clusters[J].J.At.Mol.Phys.,2009,26(3):461(inChinese)[赵严峰,田凯.MgBn(n=1-17)团簇的密度泛函理论研究[J].原子与分子物理学报,2009,26(3):461]
[6]Chopra N G,Luyken R J,Cherrey K,etal. Boron nitride nanotubes[J].Science,1995,269(5266):966.
[7]Lee R S,Gavillet J,Chapelle M L,etal. Catalyst -free synthesis of boron nitride single - wall nanotubes with a preferred zig - zag configuration[J]. Phys.Rev. B,2001,64( 12) : 121405.
[8]Hanley L,Anderson S L. Oxidation of small boron cluster ions(B+1–13)byoxygen[J].J.Chem.Phys.,1988,89(5):2848.
[9]Niu J,Rao B K,Jena P. Atomic and electronic structuresof neutral and charged boron and boron - rich clusters[J]. J. Chem. Phys. ,1997,107( 1) : 132.
[10]YangZ,YanYL,Zhao WJ,etal.Structures and magnetism of FeBN(N≤6)clusters[J].ActaPhys.Sin.,2007,56(5):2590(inChinese)[杨致,闫玉丽,赵文杰,等.FeBN(N≤6)团簇的结构与磁[J].物理学报,2007,56(5):2590]
[11]Fakihoglu E,Yurun Y,Veziroglu T N. A review of hydrogen storage systems based on boron and its compounds[J]. Int. J. Hudrogen Energy,2004,29( 13) : 1371.
[12]Yildirim E K,Guvenc Z B. A density functional study of small Li – B and Li – B – H clusters[J]. Int. J.Hydrogen Energy,2009,34( 11) : 4797.
[13]RRuan W,Xie A D,Yu X G,etal. Hydrogen storage capabilities of the most stable isomers of NanBm(m+n=6)clusters[J].Chin.Phys.B,2011,20(4):043104.
[14]Ruan W,Xie A D,Yu X G,etal. Density functional study of small Na - Bclusters[J].J.Sichuan Univ.:Nat.Sci.Ed.(四川大学学报:自然科学版),2011,48(1):99.
[15]Ruan W,Xie A D,Yu X G,etal. Geometric structure and electronic characteristics of NaBn(n=1-9)clusters[J].ActaPhys.Sin.,2012,61(4):043102(inChinese)[阮文,谢安东,余晓光,等.NaBn(n=1-9)团簇的几何结构和电子性质[J].物理学报,2012,61(4):043102]
[16]LiQS,JinQ.Aromaticity of planar B-5anionin the MB5(M=Li,Na,K,Rb,andCs)andMB+5(M=Be,Mg,Ca,andSr)clusters[J].J.Phys.Chem.A,2004,108(5):855.
[17] LiQS,GongLF.Novelpyramidal MB7(M=Li,Na,K,Rb,orCs)species:structure and aromaticity[J].J.Phys.Chem.A,2004,108(19):4322.
[18]Zhao Y Y,Zhang M Y,Xu S H,etal. Density functional theory study of the B10,and clusters and their sandwich - type metal compounds[J].Chem.Phys.Lett.,2006,432(4-6):566.
[19]LiSJ,ShiDP,ChengZF,etal.Investigation of configuration and property of YnN(n=2-12)clusters[J].J.At.Mol.Phys.,2011,28(3):427(in Chinese)[李顺江,石东平,程正富,等.YnN(n=2-12)团簇的结构与性质研究[J].原子与分子物理学报,2011,28(3):427]
[20]Yang C L,Zhu Z H,Wang R,etal. Analytical potential energy functions of the neutral and cationic2[J].J.Mol.Struct.:Theochem,2001,548(1 -3):47.
[21]Huber K P,Herzberg G. Molecular spectra and molecular structure. / IV,Constants of diatomic molecules [M]. New York: Van Nostrand Reinhold,Cop,1979: 64.
[22]Ihsan B. Systematic ab initio investigation of bare boron clusters: Determination of the geometry and electronic structures ofBn(n=2–14)[J].Phys.Rev.B,1997,55(24):16426.
