渔业管理中TAC制度的实施及其动态调整
2015-09-19张博刘庆
张 博 刘 庆
一、引言
我国正在大力发展海洋经济,而海洋捕捞业是海洋经济中的支柱产业。然而,近年来由于海洋污染和过度捕捞,使得我国主要的传统渔场大多有所退化,甚至出现“荒漠化” 现象[1][2][3]。 因此, 对海洋捕捞实施有效管理是当务之急。
纵观全球,各沿海国家的海洋捕捞业管理措施大体可分为两类:投入控制和产出控制。投入控制也可称为间接控制或传统的渔业管理,它通过入渔许可、禁渔区和禁渔期、渔具种类和规格、最低可捕标准、网目尺寸等规定来限制和调节捕捞量。世界沿海国从19世纪初开始陆续应用该制度。但是这种制度不能控制渔获量、存在制度性的缺陷,随着渔业捕捞技术的发展,渔业生产效率的提高,容易导致渔获量过大的结果,从而造成渔业资源的衰退。到了20世纪70年代,许多国家为了弥补投入控制制度的不足,在使用投入控制措施的同时,逐步开始在其渔业管理中运用单船渔获量限制制度、总可捕量制度(TAC制度)、个体配额制度(IQ制度)和个体可转让配额制度(ITQ制度)等产出控制制度。
在实践中,目前世界上渔业大国包括美国、加拿大、荷兰、冰岛、新西兰、澳大利亚等已广泛使用TAC制度,渔业资源保护与恢复效果明显,积累了丰富的经验。早期,美国为了进行规范化的渔业管理和保护渔业资源,实行了严格的限制准入和总可捕量(TAC)制度。随着时间的推移,当限制准入和TAC制度与现实矛盾激化,“竞赛式”捕捞现象愈发严重,渔业资源遭到很大的破坏,个体可转移配额制度(ITQ)应运而生。日本在近海的渔业捕捞中,使用的不是领土使用权管理体系,而是使用通常的TAC管理制度;整个国家对于某一些鱼类的TAC设定好之后,通过地方政府以及渔业管理组织(Fisheries Management Organizations,FMOs)控制各个商业捕捞船队的捕捞量。与日本、美国类似,加拿大也通过实行限额捕捞制度来管理渔业资源。加拿大对TAC的管理采用单个渔船配额(IVQ)制度:联邦政府按照渔船类型和传统优先权特征,并结合资源状况,将捕捞配额自上而下分配到每一条船上;除了个别省份和个别鱼种外,捕捞配额也可以进行部分转让,由此各渔业公司和渔船可以自行调节捕捞量。冰岛是世界上第一批引入ITQ渔业管理系统的国家之一。在TAC最初订立之后,冰岛渔业部每年都会更新各个鱼种的TAC,用于指导下一个渔业年的商业捕捞,TAC份额的初始分配方式因鱼种而各不相同。由于传统管理制度中的种种问题,韩国政府于1998年实施了TAC制度,虽然传统的TAC制度并没有规定个人的捕捞量,但是韩国的TAC制度却将捕捞量限制到了个人,实际上是一种IQ(Individual Quota)制度,即不可交易的个人配额制度。
我国从1999年起,实行海洋捕捞计划产量“零增长”控制计划,实施捕捞限额制度,开始推行产出控制管理。2000年修改颁布的新版 《渔业法》,表明我国从投入控制走向产出控制,对渔业实行投入产出“双控”管制。但到目前为止,我国尚未出台捕捞限额制度的实施细则,其主要原因之一就在于TAC确定的困难。
本文讨论的正是TAC的确定。我们注意到,制定TAC,要涉及其两方面的因素。一是近期消费者的利益,二是长期海洋生态平衡。若TAC制定过低,近期消费者的利益将遭受损失;从长期来看,若制定过高,则鱼类的生长将遭到严重的破坏,导致海洋生态失衡,甚至更为严重的可能性是,这会导致某一特定海域生态系统的崩溃。因此,制定TAC要同时考虑上述两方面的因素。换一种角度说,制定TAC,既要考虑经济因素,也要考虑生态因素。所以,具体地制定TAC,应当由海洋生态学者和海洋经济学者的合作来完成。
学术界对于TAC的研究已有一些,但尚未出现有广泛影响的方法。Dew(2001)[4]建立了一个动态调整TAC的递归模型,其中多个环节存在大量的主观判断。林龙山等(2006)[5]运用Fox模型和东海检测数据实际计算了东海区小黄鱼的TAC,但仅仅采用一个简单的Fox方程式使得文章中对于TAC的估算还是过于粗略。 Laham和 Krishnarajah(2012)[6]用logistic生长函数来研究马来西亚罗非鱼的TAC的制定。这些文献中大多都只考虑了海洋生态因素而忽略了经济因素,即使对经济因素有所提及,也极其含混。因此,这些文献中所提出的方法都存在缺陷。本文将同时考虑海洋生态因素和经济因素,为TAC的确定及其动态调整提供一种理论方法,并利用我国渤海湾渔业数据,对相关TAC进行了数值模拟。
二、模型建立及分析
考虑一个特定海域中有一种特定的鱼种。记x为该鱼种的总储量,c为该鱼种的捕捞速度。假设每年的TAC皆被精确地执行,更确切一点,假设每个时刻,皆有c=TAC。假定该鱼种的生长函数为f(x)。
假定该鱼种的市场价格为p,捕捞成本恒为常数ω>0。那么,此鱼类企业的捕捞利润为π=pcωc,其另一称谓是生产该鱼类的企业的生产者剩余。
假定鱼类消费者的效用函数 U(c,m)=u(c)+m,其中c为该鱼类的消费量,m为其所持有的货币,而u满足u(0)=0, u′> 0, u"< 0, 并且假定每个消费者都只存活一瞬间。假定消费者持有的初始货币M>0足够大,那么,消费者所要解决的问题就是
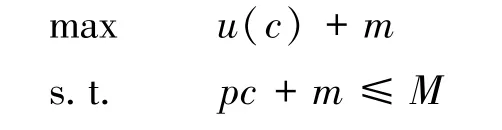
此问题等价于:max u(c)-pc
其唯一解满足: p=u′(c)
这正是该鱼类的需求函数的逆函数。而S=u(c)-pc正是消费该鱼类的消费者剩余。
假定经济体中此类企业的个数为n,消费者的个数为N。为了简单起见,我们可以假设n=N=1。但注意,这并不等同于垄断。我们做此假设,仅仅是数学上处理简单而已,而在本质的经济学意义上并没有改变多企业多消费者的情形。
我们还假定在任何时刻,该鱼种市场出清。此时,如果我们采用生产者剩余与消费者剩余之和来刻画此种鱼类的生产和消费活动所带来的总社会福利,那么,该鱼种捕捞量(消费量)为c时,总社会福利将为:
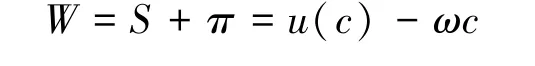
那么,社会最优的捕捞路径应当是以下优化问题的解:
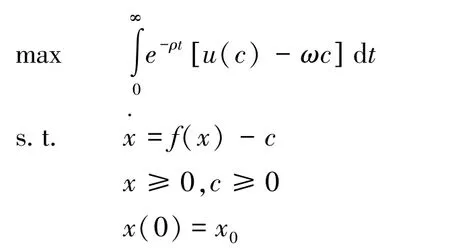
其中ρ>0为社会折现率,x0>0为初始储量。
我们来解这个优化问题。它的当前值Hamilton函数为:
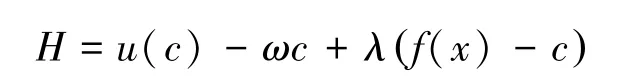
其最优解一定满足:
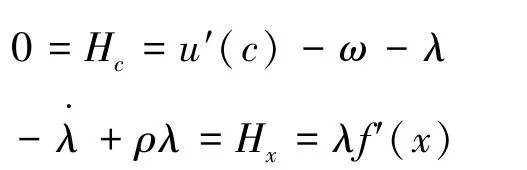
于是,
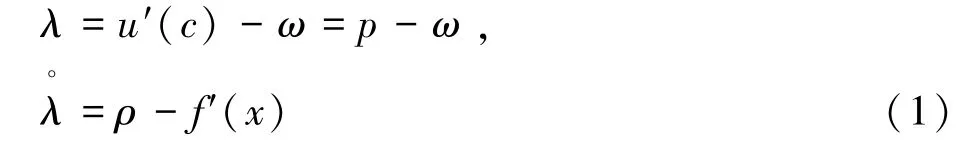
我们可以称(1) 式为 Generalized Hotelling Rule,其一等价形式为

此式左边的两项可分别解释为捕捞所获得的货币资本的增长率和持有这片海域的该鱼类捕捞权所拥有的物质资本(鱼)的增长率,这二者之和可称为持有这片海域此鱼类捕捞权的IRR(internal rate of return内部收益率或真实收益率)。那么,(2)式就可以解释为社会最优的鱼类捕捞权的IRR应与社会折现率相等。
由此可得到,最优路径应满足以下二维动力系统:
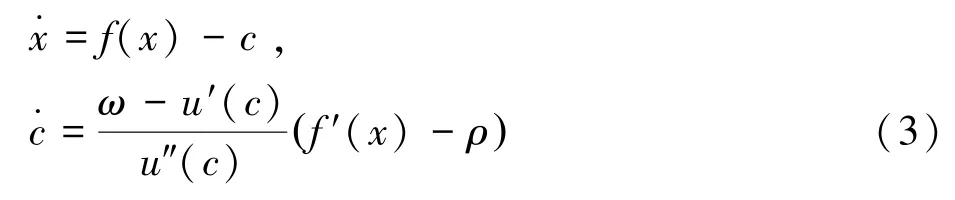
其中(3)式即为著名的Keynes-Ramsey rule。
为了便于分析,我们进一步地假设f,u的具体的解析形式。我们采用logistic函数来描述该鱼种的生长函数:f(x)=rx(1-x/K) , 其中 r > 0为该鱼种的本性生长率,而K>0为此海域对该鱼种的最大可承载力;而消费者的瞬时效用函数为 u(c)= A其中θ∈(0,1],而A>0,特别地,当θ=1时, 有 u(c)=A ln c。
这样一来,上述动力系统就有更明确的形式:
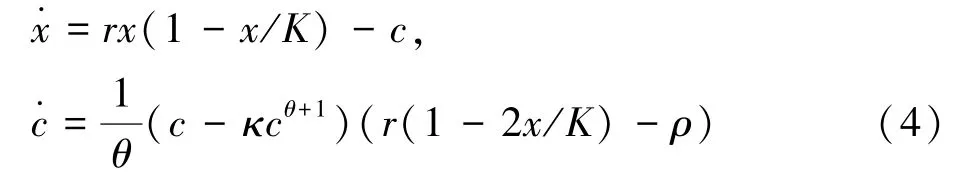
其中κ=ω/A,而第二个方程也可以写成:
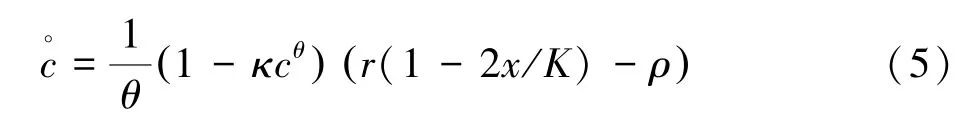
可以证明,上述优化问题的最优路径就是上述动力系统的鞍轨,即最终趋向于鞍点的那条唯一的轨道。而这个鞍点 x∗,c∗( )即为
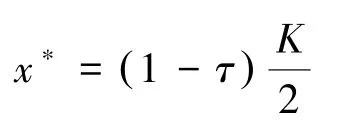
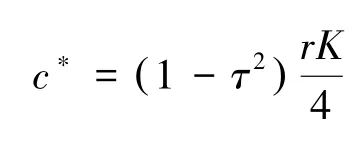
其中τ= ρ/r。
三、参数校准与数值模拟
(一)参数校准的方法
这里有六个参数ρ、r、K、θ、ω、A。随着ω >0从小变大,上述动力系统将分别有一个,两个和三个均衡点。而这六个参数具体的取值,可利用渔业历史数据对模型进行校准(calibration)。
关于效用函数的校准,我们的处理如下:
由 Ac-θ=u′(c) =p, 得: ln p=ln A- θln c。
这样,A,θ的值就可以由ln p对ln c做线性回归来得到。显然,θ就是价格的需求弹性。
而关于生长函数的校准,我们的处理如下。将模型转化成离散时间模型,再令:

其中Δxt=xt+1-xt。然后,做y向x,x2的线性回归,即考虑回归方程:
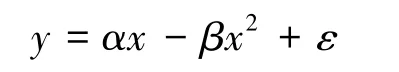
我们采用最小二乘法来得到最优的α、β,此应为以下优化问题的解:

如果能够得到鱼的总储量x的历史数据,那么,利用上述回归方程就可以求出α、β,进而得到生长函数的参数的校准。这里我们直接令回归截距为0,而这是在海洋生态学上,在纯自然状态下是成立的。当然,如果考虑海洋污染问题,截距可能为负的。那就必须拓展我们的模型。而我们的模型只是初步的,没有考虑污染问题。
而现在问题是,鱼的总储量x是没有直接的数据的,通常都是基于海洋生物学而估计出来的。这里,我们给出一种方法。
在渔业经济学中,经常被采用的捕捞量函数是所谓的Schaefer函数,即:
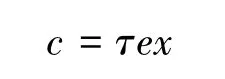
其中τ>0是常数,而c、e、x分别为捕捞量,捕捞努力,总储量。所谓捕捞努力,我们可以采用所有捕捞船只的总吨位来刻画。这样一来,只要给出τ>0,由历年的捕捞量和捕捞努力数据就可以计算出历年的储量数据。而有了储量,就可以再来采用上述回归方程来得出回归系数α、β。这样得到的回归系数自然依赖于τ,因此,我们记之为α(τ)、β(τ)。事实上,针对于给定的捕捞量历史数据,不难得出α(τ)、β(τ)的解析形式。而最终最优的 τ的确定,我们采用以下方法来解决,它应当是以下优化问题的解:
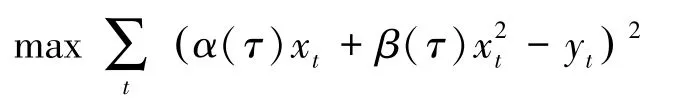
若要使得问题在形式上显得更紧凑一些,我们可以将上述两个优化问题合并成一个更大的优化问题,它的解既给出了最优的τ也给出了相应的α(τ)、β(τ):
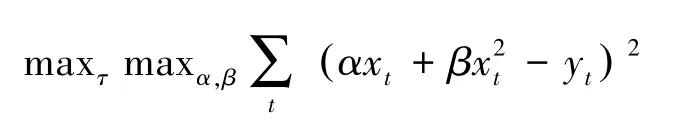
而关于社会折现率ρ,它的确定非常主观。事实上,我们的模型是一个“二合一”的模型,即我们是把一代一代的“全人类”紧缩为一个具有代表性的人物,由他来决定各个时间段的消费,然后,我们又将其解释为或理解为各个不同代人的消费。当然,这是有问题的。早在当年Ramsey考虑他的最优消费问题时就已经注意到了这个问题。我们的模型所要刻画的,从根本上说,还是一代一代的“全人类”的福祉问题,那么,这个ρ的存在就预示着对后代人的歧视。因此,在Ramsey的处理中,他是让ρ=0。但是,如果我们把问题看成一个特定的人对自己整个一生的消费的安排的话,那么,这个ρ刻画的是他对时间(或未来)的忍耐性,它的出现被一些学者认为是可接受的,比如,Arrow(2004)[7],其中他们将ρ确定在0到0.5个百分点。而在我们这里的问题中,既考虑到代际公平又为了方便,我们不妨将ρ确定为ρ=0。此时的Keynes-Ramsey rule为:
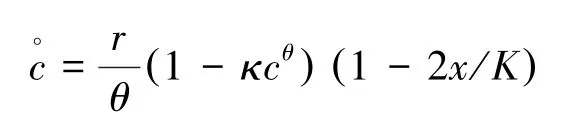
经校准得到这些参数之后,上述动力系统(4)式就给出了我们动态调整TAC的方法,其中特别是Keynes-Ramsey rule(5)式是非常方便的,它给出了TAC增长率的确定方法。
这里还有一个关键问题,那就是在给定x0的情况下,如何确定c0。只要有了c0,再由(5)式,就可以得到每年的TAC了。
最终确定c0,可采用如下方法:首先由Schaefer函数给出初步的c0的猜测值,然后,由于最优路径一定是鞍轨(即最终趋向于鞍点的那条路径,它是唯一的),那么,我们就来观察由这样的c0的猜测值出发而模拟出的路径(经由上述动力系统)是否收敛到鞍点,若偏差较大,可不断地调整猜测值直至误差在满意的程度之内。之所以还要调整由Schaefer函数给出的值,是因为这一函数本身就是对捕捞量和储量之间关系的一种粗略近似。
正如上述所提到的,在具体的应用中,我们可以令ρ=0。这样一来,就有x∗=K/2,这是该鱼类的生长速度(或说再生速度)最快的储量。让鱼类最终稳定在这个储量是最令人满意的,每代人都将可持续地享有最丰盛的鱼类盛宴。
此外,还需注意一点。一旦我们确定的一个可允许的误差范围,那么,满足这一误差标准的c0也有很多值,而在这些值中,我们应当选取可以使得储量路径适当快地接近x∗的c0猜测值。
当然,我们这里没有考虑鱼种灭绝的问题。对于一些濒危鱼类,可采用强制的休鱼期来限制人们的捕捞。对于有灭绝可能的鱼类,我们的模型也可以进行相应的调整,比如,我们可以将鱼类的生长函数改变为以下形式:
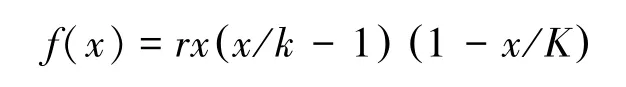
其中r>0为该鱼种的本性生长率,而K>k>0,K为此海域对该鱼种的最大可承载力,而k即为该鱼类灭绝的门槛值,即一旦鱼类储量小于这个门槛值,鱼类就将不可逆转地灭绝。
采用这一生长函数,同样可以得到相仿的动力系统,并可对其做相仿的分析,进而得出TAC的动态调整的方法。
(二)TAC动态调整路径的模拟
如果能够获得各个鱼种每年的储量、捕捞量与价格的信息,采用上面的思路我们很容易便可以校准出模型的六个参数。而关于这些参数,文献中也出现过由其他方法给出的估计。现在我们就直接采用这些已有估计对上述动力系统进行模拟。
首先,现有研究一般认为中国消费者的相对风险规避系数相对较大,一般采用θ=2(Barro,2006b;Gabaix,2008;Gourio,2008b; 陈彦斌等, 2009; 吴利学,2009)[8-12]。一方面,考虑到现代捕捞业主要是固定投入比较大,捕捞的边际成本非常小,因而,我们令捕捞的边际成本ω=0;另一方面,令边际成本为零也使得我们的系统更加容易模拟,ω>0会使得我们的动力系统非常复杂。我们令A=1,这也是参照已有研究的做法,而且在捕捞的边际成本为零时它的设置不影响模拟的结果。其次,参照Arrow(2004)[7]确定的折现系数范围, 我们将 ρ确定为0.004,事实上,使ρ在0与0.005之间都可以得到基本一致的模拟结果。最后,参照Laham和Krishnarajah(2012)[6]关于罗非鱼的生长函数的确定方法,我们令鱼的自然生长率的系数r确定为0.8,实际上令r∈ (0.5, 0.8),我们都可以得到基本一致的模拟结果。考虑到渤海湾的面积为1.59万平方公里,如果每平方米最大可以承载5条2斤左右的鱼,那么渤海湾最大可以承载9 000万吨的鱼,为了谨慎起见,我们设渤海湾的最大鱼承载量K为8 000万吨鱼。以上是我们参照已有研究校准的模型参数,要得到更加准确的模型参数,必须对于渤海湾相关渔场进行系统的研究与统计。
对于鞍点路径的模拟有很多种方法,譬如前向预测法(forward shooting)、后向倒推法(backward integration) 以及 Trimborn 等(2006)[13]所开发的更一般的方法(relaxation method)。前向预测法的主要思路是在知道鱼储量的前提下,通过插值法不断修正初始的捕捞量c0,进而最终找到这条鞍点路径。这个方法的问题在于鞍点路径对于捕捞量的初始值c0的变化非常敏感,很小的误差就可能使得我们找不到这条唯一的鞍点路径,而且目前我们没有鱼储量的数据,因此,这个方法目前是不可行的。Trimborn等(2006)[13]所开发的一般性的方法非常强大,主要是解决由于多个状态变量下倒推法不能倒推到初始点的情形,而且对于有等式约束方程的动力系统也非常有效。它也是一种前向修正的方法,首先假设一个路径而后运用牛顿法不断修正路径最后模拟出鞍点路径。Brunner和 Strulik(2002)[14]给出了另一种解决这一问题的方法,这就是倒推法,其核心思想是:把原来的微分动力系统逆转方向,这样原来动力系统的鞍点路径就逆转了运动方向(从鞍点处向两边运动),因而,便可以从原系统的均衡点开始模拟原来的鞍点路径,最后把时间方向逆转过来就可以了。这种方法非常适合我们不知道模型状态变量的初始值的时候,这也正是我们模型的情况。所以,综合起来,我们采用倒推法模拟鱼储量和鱼捕捞量的运动轨迹。
图1与图2是我们运用倒推法模拟出的鱼储量和鱼捕捞量的运动轨迹图。其中,图1模拟的是上述动力系统中的鞍轨(也就是捕捞量作为鱼储量的函数的运动轨迹)。由图1可知,红线表示捕捞量的变化率c·=0的曲线,它是垂直于横轴的一条直线,垂足处的鱼的储量是3 800万吨,曲线表示鱼储量的变化率=0,它是一条抛物线,与鱼的变化率的曲线的交点即为该动力系统的鞍点A(3 800,1 596)。直线表示鞍轨,低于均衡水平的鱼储量的初始位置都会沿这条鞍轨收敛到均衡点A。表中的箭头表示该动力系统在相关区域的运动方向。
图2中的浅色线表示鱼储量x(t)的运动轨迹,深色线表示鱼捕捞量c(t)的运动轨迹,它们都从初始水平逐渐向均衡点处的储量水平和捕捞量水平收敛并最终稳定在均衡水平上。表1给出了30期的鱼储量和相应的鱼捕捞量(TAC)的具体的数值,譬如,如果今年的鱼储量是50万吨,TAC大致应该为20万吨的捕获量。那么,在此基础上,如果能够具体估计出渤海湾的各年的鱼储量,我们便可以很容易地确定各年的TAC。
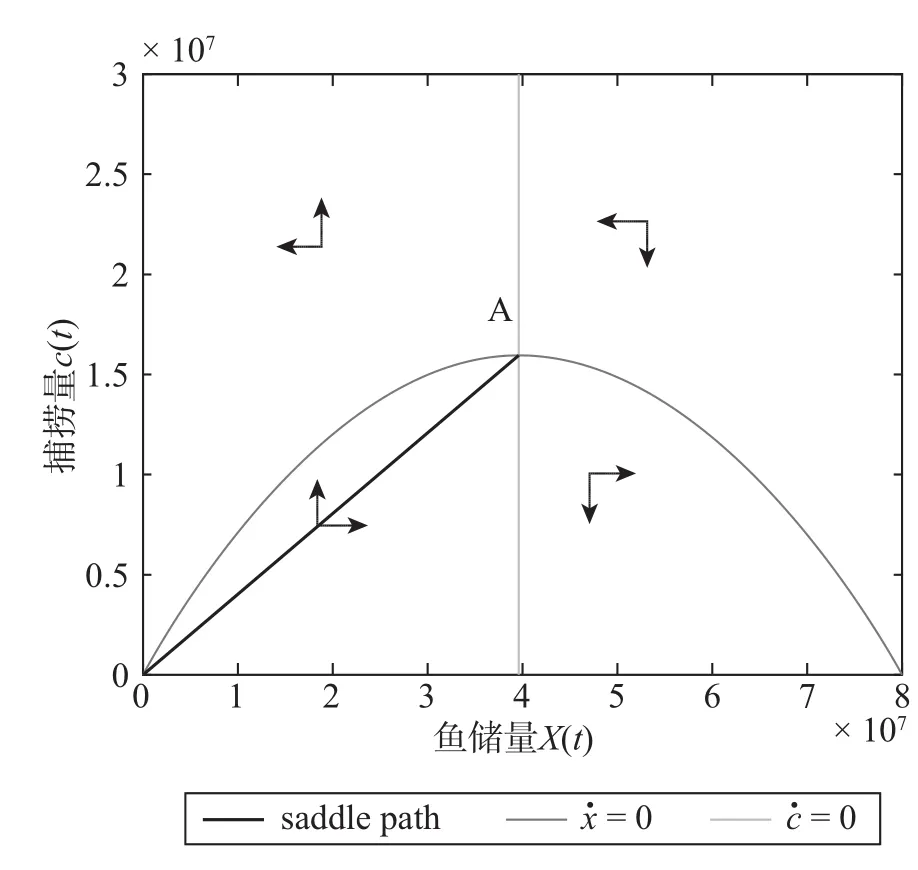
图1 鞍轨的模拟
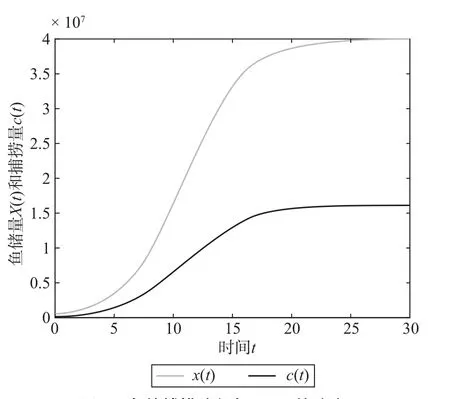
图2 鱼的捕捞路径与TAC的确定
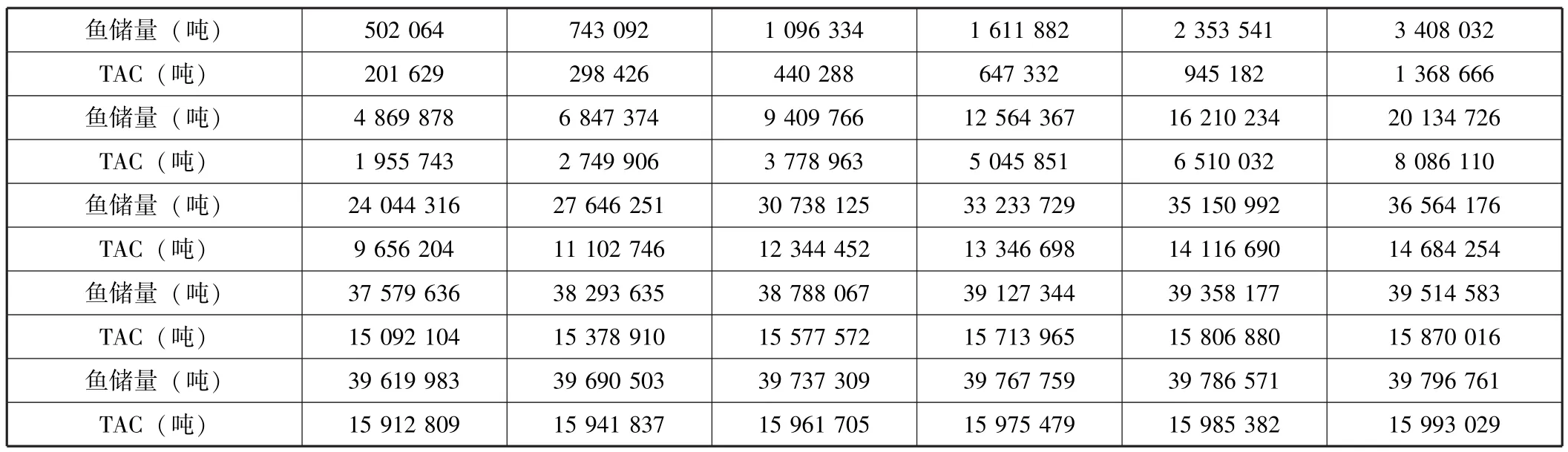
表1 鱼储量与TAC的确定
四、几点注记
(一)关于TAC被精确执行的假设
在上述讨论中,我们事实上给出的是在同时考虑经济因素和海洋生态因素的情形下的社会最优捕捞路径。而TAC在任何时刻都被确定成这一最优捕捞路径上的捕捞量。这样做的理由是,所谓社会最优是理想中的全体人类进行大一统合作(grand coalition)的结果,这样的结构应当是对人类中的每一分子都是有益的。问题是这样的大一统合作在现实中是无法实现的。在现实中,合作是经济利益驱使的,而即使有这样的形式上的合作,也会有人因所谓的“搭便车”问题而背离合作,进而使得这样的合作是不稳定的,甚至是名存实亡的。总之,合作应当是博弈的结构。到底能否实现大一统合作,每个人都根据各自的情况进行选择。因此,政府作为激励者,可以将理想中的大一统合作情形下的捕捞路径提供给社会,制定出TAC,至于这样的社会总捕捞量到底在各个捕捞者之间实现怎样的最终分配,政府给人们提供一个自愿交易的平台,由他们自行决定。此外,在现实中,有很多的不确定因素,因此,随机模型应当是更恰当的模型,其中,政府最终依然要制定明确的TAC。但由于政府无法完全掌握所有信息,因此,在任何时刻,可能由于某些不确定因素的出现,使得人们的自愿捕捞量出现变化,进而使得总捕捞量可能严格小于TAC。
(二)关于市场结构
在上述分析中,我们没有关注市场结构,我们要说明的只是社会最优的捕捞路径进而相应地给出了社会最优的消费路径以及市场价格的运行路径。但是,什么样的市场结构可以自动导出这样的经济运行路径呢?可以证明,完全竞争市场可以导出这样的经济发展路径。因此,完全竞争市场是优良的市场结构。
至于其他类型的市场结构,如垄断市场或者完全寡头市场或者存在其他形式的垄断组织如Cartel等的市场,都可以做相应的分析。特别是垄断市场,如果还像以上所假设的那样,鱼类的消费是常弹性的,那么,市场价格将有与完全竞争市场上的价格有类似的运行规律。
但是,考虑到山东省的情况,我们认为,所有的鱼种市场都近似于完全竞争市场。因此,在这里我们就只研究了完全竞争的情形。
(三)关于折现率
事实上,我们可以将上述模型中的社会折现率换成金融市场上的收益率δ,相应的折现因子为:
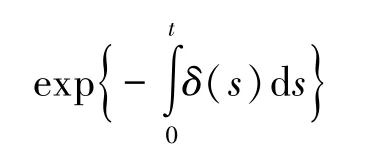
同样可以得到与(2)式类似的结果,即:

可以从No-arbitrage的角度来给出对(2′)式的解释。即,在一个运行良好的经济中,是不存在套利机会的,持有金融资产和持有鱼类资本,其收益率是相同的。
这样一来,(5)式就应相应地被调整为:

这两种折现,各有其道理。社会折现(事实上这里我们采用的是0社会折现率)所要突出的是代际公平;而金融折现,想要突出的是,货币化现金流的总价值应按金融市场上利率来折现,金融市场是所有货币化产品的基准市场。
至于到底应采用社会折现率(在上述处理中我们事实上最愿意提出的建议是将社会折现率设定为0)还是采用金融折现率,还要看模拟的结果,然后再由专家组结合其他方面的信息包括经验,做出最终的决定。
五、结论
TAC的确定需要同时考虑海洋生态因素和经济因素。在此考虑之下,我们为TAC的确定及其动态调整提供了一种理论方法,建立了一个动态模型,并利用我国渤海湾渔业数据,对相关TAC进行了模拟。根据这一理论方法,我国各海洋渔场皆可制定出各自的针对各类鱼种的TAC并动态地调整它。
