基于多中介变量的货币市场利率及预期波动对股票收益率冲击效应分解
2015-09-19尹海员乔小乐
尹海员 乔小乐
一、文献综述
很早就有研究关注于货币市场与股票市场互动关系,并从实证角度对其做出解释,这些研究主要集中于股票市场与货币需求的关系、货币市场变量对股票市场的影响。 Friedman(1988)[1]利用美国 1961—1986年的季度数据进行实证研究,发现股票市场运行与货币流通速度呈负向关系。Choudhry(1996)[2]在这一思路的基础上,对美国货币需求量、利率水平、国民收入和股票市场的时间序列数据进行分析,发现前三个变量不存在协整关系,但是加入股票市场之后,变量之间存在着长期的均衡关系。在货币市场如何影响股票市场方面, Pearce和 Roley(1985)[3]发现美国未预期到的货币供应量的增加与股票价格之间存在着负相关关系。 Ioannidis和 Kontonika(2008)[4]则利用长期数据(30年)研究了OECD国家货币政策变化对股票收益率的影响,结果支持了货币政策变化会显著影响股市收益率。国内学者比如陈晓莉(2003)[5]的研究发现我国货币供应量和上证综指之间存在长期均衡关系。肖卫国、袁威(2011)[6]对货币政策与股票收益率之间的关系进行了实证检验,发现股票收益率与货币政策存在关联的证据。
近年来部分学者开始探讨宏观货币金融变量(主要是通胀、利率政策)对股票市场的影响渠道和机制。国外学者Chen(2007)[7]发现股价波动对货币政策的这种不对称反应可以由企业面临的融资约束水平的周期性变化来解释。同样 Basistha和 Kurov(2008)[8]发现股市对货币政策变动的反应在不同经济时期的异质性根源于货币投放的信贷渠道。而Campbell和 Shiller(1988)[9], Ritter和 Warr(2002)[10]从通货膨胀或通胀幻觉(Inflation Illusion)的角度,研究货币市场利率对证券价格的影响效应。对于国内学者而言,现有研究仍然侧重于宏观货币市场运行(以通胀为主)对股票市场收益的影响,但也有学者试图从投资者行为的视角考察货币市场和股票市场之间的关系,比如说陈国进等(2009)[11],张宗新、朱伟骅(2010)[12]等。但目前这方面研究文献尚不多见。
综上,本文立足于我国货币市场和股票市场数据,在研究两者之间的互动性时,将货币市场利率及预期波动对股票收益率的冲击效应进行分解,特别将投资者情绪、违约利差因子等因素作为重要的中介变量,通过构建适当的指标,分析货币市场利率波动对股票收益率冲击效应的中介机制。
二、数据说明与指标构建
(一)股票市场运行数据
在综合考虑所有变量数据可得性的基础上,本文选取样本期间为2003年1月至2014年6月共138个月,涉及的股市和货币市场运行数据均来自于锐思(RESSET)金融数据库。
股票市场指标方面,样本个股直接计算其收益率,同时为了衡量我国股票市场的总体收益率,分别取深证成指(SZCZ)和上证综合指数(SZZZ)以样本期间的股票流通市值为权重,计算其加权平均值作为我国股票市场总体运行指标(CSMI)。通过Pearson相关检验发现CSMI与SZCZ、SZZZ的相关系数分别为0.973和0.988(双尾,1%显著性水平),这说明衡量我国股市总体运行的指标CSMI与沪深两市有着很强相关性,具体走势见图1。
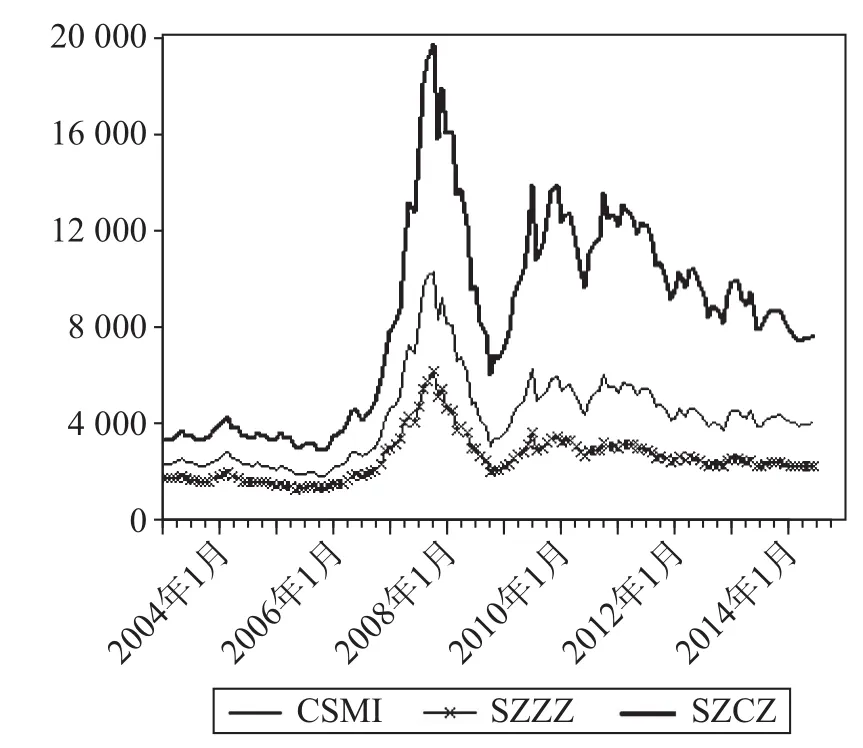
图1 2003年1月至2014年6月CSM I、SZZZ和SZCZ趋势图
(二)货币市场利率指标
货币市场利率指标方面,本文综合考虑我国市场化水平、市场容量、交易活跃程度和国内多数的研究惯例,最终采用同业拆借利率(选取一个月期)作为衡量货币市场利率的变量进行基础分析,用质押式国债回购利率(同样选取一个月期)进行稳健性检验。
关于利率波动预期部分的分解,Kuttner(1996)[13]发现美国联邦基金远期利率是衡量利率预期波动的一个非常理想的工具。然而我国的金融衍生品市场尚不发达,无法直接从市场上得到有效的远期市场利率来满足研究的需要,可以考虑通过不同期限的同业拆借利率计算出隐含的远期利率作为货币市场利率预期。根据利率期限结构理论,远期利率是对未来即期利率的预测值,即:
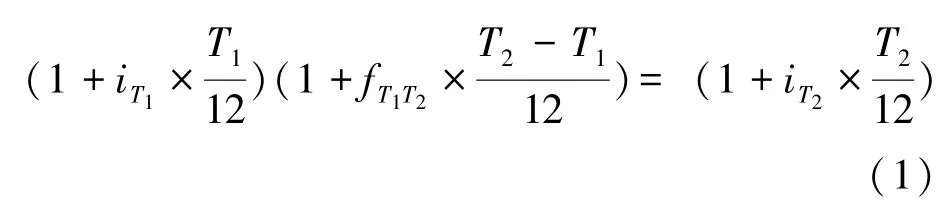
上式变形可得:
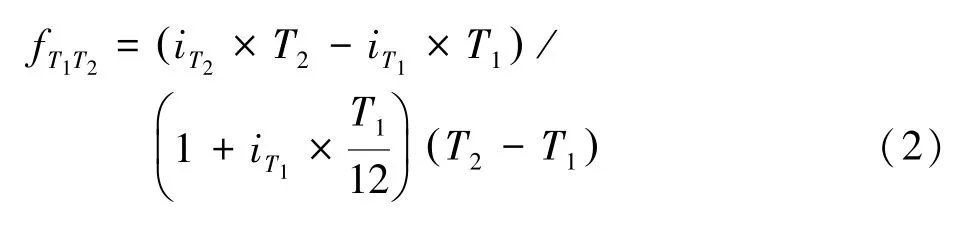
其中iT1和iT2分别表示T1,T2时刻的即期利率,fT1T2为T2-T1时间内的远期利率。本文采用1个月期的远期利率来表示投资者对未来不同月份的1个月期拆借利率的预期,考虑到样本数据的连续性,分别用以第1个月和第2个月为起点的未来1个月期远期利率f12和f23作为货币市场短期和长期利率预期的衡量指标。
(三)投资者情绪指标
对于投资者情绪的测量方法,Baker和Wurgler(2006)[14]通过两个步骤建立了比较完善的投资者情绪复合指数①具体过程见Baker M and Wurgler J.Investor Sentimentand the Cross-section of Stock Returns [J].Journal of Finance, 2006(614): 1645-1680。 国内学者易志高、茅宁参考其方法构建了一个衡量我国投资者情绪的综合指标,具体参见 《中国股市投资者情绪测量研究——CICSI的构建》,金融研究,2009(11):175-184.,并且这种复合指数的科学性受到研究者的广泛认可。基于此,本文借鉴Baker和Wurgler(2006)的方法,选择样本时间段内5种客观和主观衡量指标(封闭式基金折价率(DCEFt),沪深两市交易量(TURNt),消费者信心指数(CCIt),新增投资者开户数(NIV),IPO首日收益(IPORt))作为源指标,4种宏观经济周期变量(工业生产增加值(IAV)、月度无风险收益率(MRF)、货币供应量(MS)、消费者物价指数(CPI))进行投资者情绪指标的构建,最终构建出我国投资者情绪变量:CSI(China Sentiment Index)。
从图2可以看出,本文所构建的CSI与我国股票市场总体运行指标(CSMI)保持着较为一致的变动趋势,说明本文所构建的CSI指标较好地反映了我国股票市场投资者情绪的实际状态。
(四)违约溢价、期限溢价指标

图2 2003年1月~2014年6月我国股市投资者情绪(CSI)与市场总体指数(CSIM)关系图
在分析货币市场利率及预期波动对股票收益率的冲击效应过程中如何控制影响股票收益率的关键因素非常重要, Petkova(2006)[15], Hahn 和 Lee(2006)[16]的研究表明违约利差和期限利差是捕捉Fama-French定价因子中信息因素的重要状态变量,前者反映了对未来信贷市场环境的预期,后者反映了市场对未来期限溢价的预期。本文采用中信标普债券指数②中信标普债券指数开发和计算始于1999年12月30日,是中国国内最早、体系完备的债券系列指数,分别追踪中国国债、企业债、银行间债和可转债市场的业绩表现以及具有综合意义的全债指数,是使用最广泛的中国债券市场和固定收益投资策略的业绩衡量基准。收益率来计算违约利差,选取中信标普企业债指数收益率和国债指数收益率来表示公司债券收益和国债收益情况,两者之差来表示违约利差;期限利差为10年期和1年期国债到期收益率之差。违约利差因子和期限利差因子分别表示为ΔDEFt,ΔTERMt。
(五)熊市和牛市的阶段划分
在不同市场环境下(牛/熊市)投资者行为会有不同的反应模式,目前各学者关于牛/熊市的划分方法主要有参数和非参数两种方法。本文借鉴Pagan和Sossounov(2003)[17]的非参数方法, 将波段的单向运行周期设定为5个月,并且根据公认的观点,如果股市从上个低位(高位)整体增加(降低)20%,则构成了牛市或者熊市,便可忽略最小单向运行周期5个月的要求。选取CSMI月度数据,对样本期间中国股市的牛熊市阶段进行划分,绘制图形如图3。
由图3可知,2003年1月到2014年6月我国股票交易市场共有7个牛市和熊市的循环。同时由图可以看出中国牛熊市阶段变换的特点正好与我国2007年间股市持续上涨泡沫膨胀,而2008年遭受金融危机影响股市大幅下跌的现实相吻合。
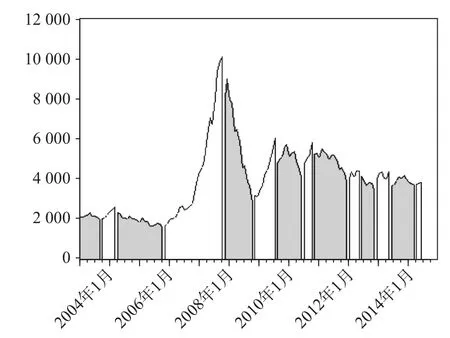
图3 2003年1月至2014年6月中国股票市场的牛熊市周期
三、不同市场环境下货币市场利率及预期波动的冲击效应
(一)基础模型
考虑到货币市场利率波动在不同市场环境下对股市收益率的冲击可能会存在异质性反应,投资者情绪、违约利差因子和期限利差因子在牛市和熊市中的中介作用也可能不同,所以本文引入虚拟变量来分析这种区别。同时本文通过将货币市场利率预期纳入分析模型,以探讨利率预期的波动在不同市场环境下对被解释变量影响的异质性。为了控制宏观经济变量对因变量的影响,解决内生性问题和遗漏变量问题,本文加入通货膨胀增长率和工业生产增加值两个解释变量,之所以加入这两个变量是因为它们是货币市场和股票市场都较为关注的指标,同时月度数据较为完备。
综上考虑,本文用带有自回归的方程(3)来估计被解释变量对货币市场利率水平、利率波动预期、市场环境、宏观经济运行等因素的反应:

其中Yt为t期的被解释变量;Dt为牛熊市状态的虚拟变量,在牛市状态下Dt=1,在熊市状态下Dt=0;IBO1Mt为1个月期同业拆借利率,反映货币市场即期利率水平;f12t和f23t分别表示t时刻货币市场短期利率预期和长期利率预期;γ1、γ3和γ5反映了熊市中被解释变量对货币市场利率、利率波动预期(包括短期和长期预期)的平均反应程度;而γ2、γ4和γ6反映了不同市态下被解释变量对货币市场利率、利率波动预期的平均反应程度的差异;CPIrt和IAVt分别表示通货膨胀增长率和工业生产增加值两个宏观经济变量;εt表示影响被解释变量的其他因素。如果考虑到被解释变量平稳性,需要在公式(3)右边加入被解释变量滞后期项
经过肯德尔τ非参数相关性检验,各个变量之间的相关性很低,序列相关性对估计结果的影响不大。为了保证时间序列的平稳性,首先进行单位根检验,表1显示了各变量的描述性统计和单位根ADF检验结果。

表1 变量描述性统计与平稳性检验
从表1可以看到,所有变量都拒绝正态分布假设。并且根据ADF方法得出的单位根检验结果表明,上述变量都是平稳时间序列。
(二)货币市场利率及预期对股市收益率的冲击效应
考虑到模型变量的非正态性,将股票市场收益率(CSMI rt)作为被解释变量,根据模型(3)采用广义误差分布的EGARCH模型进行估计,同时由于CSMI rt是平稳时间序列,因而不必加入被解释变量的滞后项。表2给出了EGARCH模型估计结果,模型估计后的方差经ARCH-LM检验统计量Obs∗R-squared为1.46,伴随概率为0.69,说明EGARCH模型的残差序列不再存在ARCH效应。
表2的回归结果显示我国货币市场即期利率及利率预期对股市收益率的冲击在不同的市场环境下呈现明显的差异和非对称性,具体分析如下:(1)首先对于货币市场利率的即期水平而言,γ1和γ2都在5%的水平下显著,说明货币市场即期利率的变化在牛熊市中对股市收益率都有显著性影响,具体而言γ1等于-8.07,这表明1个月期同业拆借利率每上升1%,熊市中股市收益水平会下降8.07%,而牛市中的这种负相关效应要差一些,负相关系数为-3.34(γ1+γ2)。(2)货币市场中的短期利率预期f12的系数γ3和γ4分别在5%和10%水平下显著,说明货币市场中的短期利率预期对股市收益率是有显著影响的。具体而言 γ3和 (γ3+γ4)分别为-6.30和-3.21, 这表明短期利率预期f12每降低1%,熊市中股市收益水平会上升6.30%,而在同样条件下牛市中股市收益率会上升3.21%,显然熊市中短期利率预期对股市影响更大。(3)货币市场中的长期利率预期变量f23的系数γ5在10%水平下显著,而系数γ6并不显著,说明长期利率预期在熊市中对股市收益有显著影响,而在牛市中对股市收益却没有显著影响。具体而言γ5等于-2.19,说明f23每上升1个百分点,熊市中股市收益水平会下降2.19%。

表2 货币市场利率及预期波动对股票市场收益率的冲击效应
将投资者情绪 (C SIt)作为被解释变量,继续根据基础模型(3)采用广义误差分布的EGARCH模型进行估计,表3给出了EGARCH模型估计结果。尽管CSIt是平稳时间序列,但由于它与其滞后1期CSIt-1有很强的相关性,为了提高模型精确度,在模型中增加了滞后项CSIt-1作为其解释变量。模型估计后的方差经ARCH-LM检验统计量Obs∗R-squared为3.82,伴随概率为0.28,说明EGARCH模型的残差序列不再存在ARCH效应。
表3结果可以看出,投资者情绪具有一定的粘连性,前期情绪会在1%的显著性水平上影响当期投资者情绪。另外货币市场利率及预期对投资者情绪的冲击在不同的市场环境下也呈现出了异质性:首先,对
(三)投资者情绪对货币市场利率及预期波动的反应
于即期利率水平而言,在熊牛市状态下IBO1M对投资者情绪影响的系数γ1和γ1+γ2分别为-3.02和-1.98,并通过了在5%和10%水平显著性检验,这说明货币市场即期利率水平的波动对投资者情绪产生了显著影响,利率上升将会带动投资者情绪转向悲观,同时熊市环境下这种冲击效应要强于牛市。其次,货币市场短期利率预期f12的系数γ3和γ4分别在5%和10%水平下显著,γ3和 (γ3+γ4)分别为-2.14和-1.18,这表明f12每降低1个百分点,熊市中会刺激投资者情绪上升2.14个百分点,而在同样条件下牛市中投资者情绪上升1.18个百分点。再次,货币市场长期利率预期f23的系数γ5和γ6并不显著,这说明货币市场中长期利率波动预期对投资者情绪没有显著影响。

表3 投资者情绪对货币市场利率及预期波动的反应
综合(二)、(三)部分回归结果,股市收益率对即期利率波动(IBO1M)和长短期利率预期波动(f12,f23)反应比较显著,而投资者情绪对即期利率波动(IBO1M)和短期利率预期波动(f12)表现出了显著性的反应,却没有受到长期利率波动(f23)的影响。
从牛熊市不同的市场状态看,无论股市收益率还是投资者情绪对货币市场利率及利率预期的反应,熊市的反应都显著大于牛市。这种影响效应的异质性表明,在熊市中投资者面对市场资金面流动性紧张的情况下,相信并且非常依赖货币当局救市的行为和能力①国外研究中也发现了投资者对政府监管部门干预熊市的依赖性(Doms&Morin,2004;Petkova,2006),比如美国证券市场中将美联储经常通过降息等量化宽松政策来提振股市并恢复投资者信心的政策称为“格林斯潘对策”(Greenspan Put)。。从行为金融理论的角度看,这一现象比较合理的解释是投资者“有限注意力”。在投资者有限注意力的假设条件下, Klibanoff等(1998)[18]和 Peress(2008)[19]都指出,当信息被更突出地在新闻媒体报道时,股价对该信息的反应速度会更快。看起来,投资者在熊市中会花更多的注意力去关注并跟踪货币市场利率水平的波动,造成这种现象的原因可能是在熊市中,媒体会对市场资金供给关系水平给予更多的报道,并且由于央行长期以来在熊市中往往成为流动性的最终提供者。这样投资者注意力水平的提高可能会造成货币市场利率变化对投资者情绪、股票收益水平的冲击效应的提高。上述结论给了我们一个启示:股票市场收益对货币市场利率波动的非对称性是否来自货币市场利率及预期波动对投资者情绪的影响?②一种可能的疑问是货币市场利率波动对投资者情绪的冲击是由于其首先对股票市场收益水平的影响,进而由股价波动影响到情绪变化。为了验证这一疑问,本文将CSMI收益作为解释变量纳入投资者情绪CSI作为被解释变量的模型进行回归,结果显示其回归系数并不显著。限于篇幅,结果未在正文中列示,感兴趣的读者可以联系作者索取。本文将在第四部分对此进行验证。
(四)违约溢价、期限溢价对货币市场利率及预期波动的反应
将违约利差 (Δ DEFt)和期限利差 (Δ TERMt)分别作为解释变量,仍然根据基础模型(3)采用广义误差分布的EGARCH模型进行估计,表4给出了估计结果。两个模型估计后的方差经ARCH-LM检验统计量Obs∗R-squared分别为0.49和1.94,伴随概率为0.02和0.58,说明EGARCH模型的残差序列不再存在ARCH效应。
表4的回归结果显示,对于违约利差因子而言,即期利率 (I BO1M)的变化无论牛熊市环境下都会对其产生正向影响,且均在5%水平下显著,但熊市中的影响要强于牛市环境 [γ1=0.18>(γ1+γ2=0.07)]。这表明IBO1M上升1个百分点,熊市中的违约利差溢价会上升0.18%,在相同条件下牛市中上升0.07%,说明熊市中违约利差因子对利率波动更为敏感。短期利率预期 f12( )对违约利差因子的影响效应与即期利率类似,熊市中影响效应要强于牛市。长期利率预期对违约利差因子只在熊市环境下产生影响,系数为0.05,要低于IBO1M和f12的影响程度。
对于期限利差因子而言,货币市场利率及预期波动对其影响均呈现负向关系,但大多不显著。只有在熊市中即期利率水平 IBO1M( )和短期利率预期 f12( )对其有显著的影响:前者系数-0.27,这表明IBO1M上升1个百分点,熊市中的期限利差水平会下降0.27%;后者系数为-0.02。总之,表4的回归结果表明,牛熊市中货币市场利率及利率预期波动对股票市场收益率的冲击效应的根源很可能是来自于这些波动影响了投资者对信贷环境的预期。
四、货币市场利率对股票收益率冲击效应的进一步分解研究
(一)研究假设与样本股票选取
本部分重点分析货币市场利率及预期对股票收益率的影响效应中,投资者情绪、对信贷环境的预期等中介变量是否起到关键性的传递作用。根据前文分析,一个可能的假设是货币市场利率及预期波动对股市收益率的冲击很可能来自于前者影响了投资者情绪、信贷环境预期等因素,进而影响股票收益率的波动。如果对投资者情绪、信贷环境预期、个股风险等因素更敏感的股票收益率受到货币市场利率波动的冲击程度更大,上述假设就能得到检验证实。
本文选取从2003年1月至2014年6月沪深两市的上市公司A股为样本,观测值小于138个月、PT、ST类样本股票被剔除掉后,共选取397个公司作为样本股票,样本股票按全球行业分类标准共涵盖了能源、原材料、工业、非日常生活消费品、日常消费品、医疗保健、金融、信息技术和公用事业9大类①全球行业分类标准(GICS)将上市公司股票共分为10类,由于我国电信业务类在2003年1月之前上市的公司只有两家,为了便于后续分析,本文将电信业务合并入信息技术行业。。
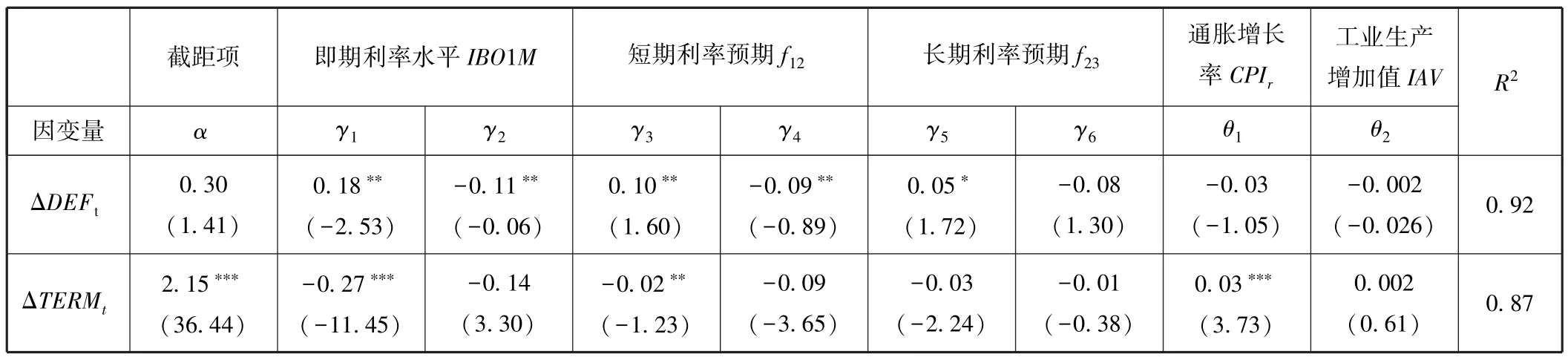
表4 违约利差及期限利差对货币市场利率及波动预期的反应
(二)货币市场利率及预期的冲击效应的分解
为了检验投资者情绪、系统风险、信贷环境预期和期限溢价等变量在货币市场利率波动对股票收益率冲击效应中的中介作用,本文进行如下3步分析:
1.对样本股票月度收益率进行如下回归:
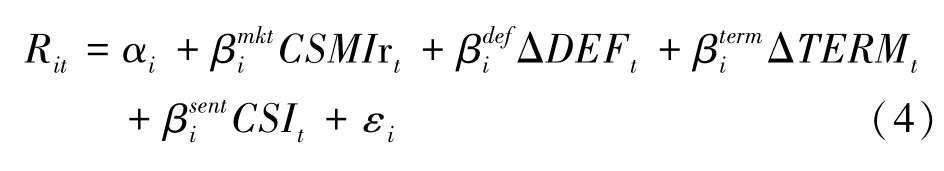
其中CSMIrt是上文CSMI指数的超额收益率;CSIt是投资者情绪;ΔDEFt、ΔTERMt分别为违约利差因子和期限利差因子;回归系数分别衡量样本股月度收益率对市场超额收益、违约溢价(实际代表信贷市场环境)、期限溢价和投资者情绪的敏感程度。表5显示了模型(4)回归系数估计值的描述性统计和相关性分析,肯德尔τ非参数相关性检验,各个变量之间的相关性较低。
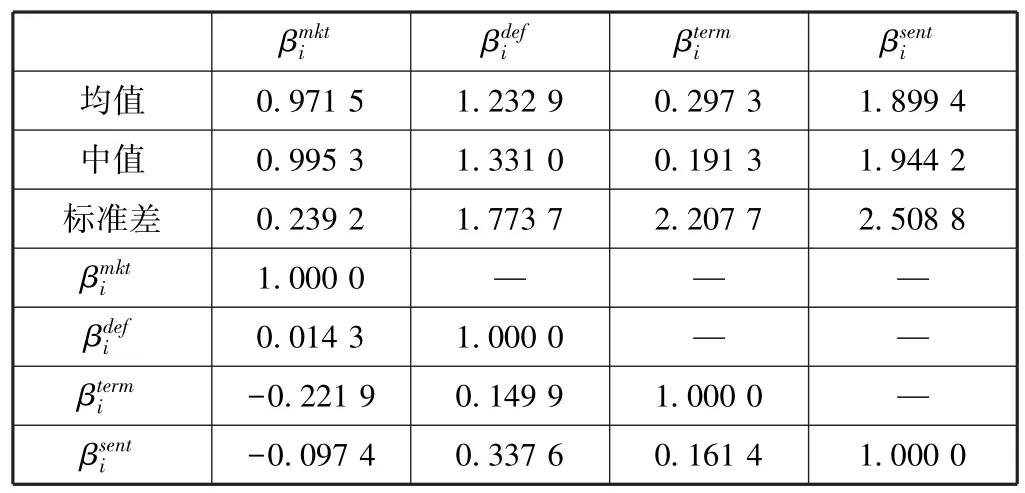
表5 样本股票面板数据分析回归系数的描述性统计以及相关性
2.对样本股票月度收益率进行货币市场利率及预期波动的回归分析:
借鉴上文的基础模型(3),去掉自变量中的滞后项变形为模型(5),对样本股票月度收益率进行截面数据分析,这些回归系数估计值的描述性统计结果显示在表6中。


表6 样本股票收益率对货币市场利率及预期波动的回归系数描述性统计
3.对模型(5)的回归系数进行影响因素分解。
为了解释样本个股对货币市场利率及预期波动的反应的异质性,接下来对公式(5)中的系数(γi或者γi+γj)估计值进行影响因素的回归分析,以验证那些对投资者情绪、信贷市场环境等中介变量的变化更为敏感的股票,是否会对货币市场利率波动有更强的反应。本文估计了如下的截面回归:
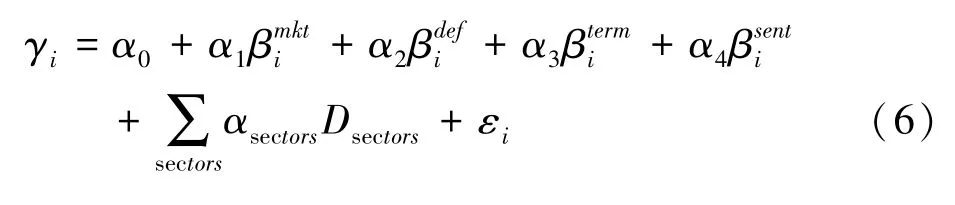
其中γi为方程(7)中分别对每只股票估计的它们分别代表不同的货币市场利率波动变量在不同市场环境下对样本股票收益率的冲击效应系数;分别为根据方程(4) 计算出的市场超额收益、违约利差、期限利差和投资者情绪的因子载荷系数。为了简化对于系数的比较和解释,所有的因子载荷系数均进行标准化处理。模型(6)的回归估计结果见表7,其中共进行了6次回归,分别用模型表示。
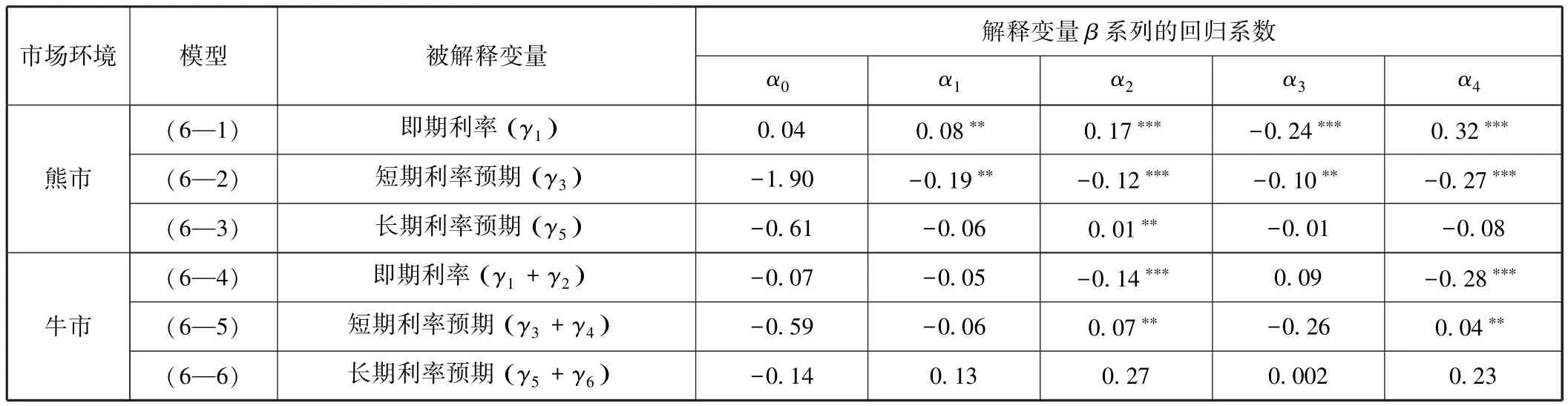
表7 牛熊市环境下货币市场利率冲击系数的分解结果
表7的回归结果归纳如下:
1.牛市环境下的回归模型(6-4) 和(6-5)结果显示,α2和α4都通过了显著性检验,即期利率和短期利率预期波动对股票收益率的冲击效应中,更多来自于违约利差因子和投资者情绪的贡献,即期利率水平和短期利率预期的提高首先会造成投资者对未来信贷环境恶化和上市公司融资难度增大的担心,并影响到其情绪,进而降低了其对股票收益率的预期。而模型(6-6)所有的解释变量都不显著,印证了牛市环境下长期利率预期对股票收益率没有显著影响。这些结论与第四部分中表2和表3的结论相一致。
2.熊市环境下, 回归模型(6-1) 和(6-2)的所有解释变量系数都通过了至少5%水平上的显著性检验,说明对投资者情绪、系统风险、违约利差和期限利差更敏感的样本股票的收益率,更容易受到货币市场即期利率和短期利率预期波动的冲击。投资者情绪等变量在冲击效应的传导过程中充当着重要的中介作用。回归模型(6-3)中只有α2显著,说明熊市中投资者对货币市场长期利率预期波动的忧虑只是来自于信贷环境的恶化。
3.从不同货币市场利率变量角度看,熊市环境下不同货币市场利率变量对股票收益率的冲击效应分解中,多数自变量通过了显著性检验,牛市环境中只有即期利率和短期利率预期有自变量通过了显著性检验,而且熊市环境下的冲击效应的系数绝对值普遍大于牛市环境。这进一步验证了第四部分的实证结论:货币市场即期利率、短期利率预期的波动在任何市场环境下都会对股票收益率造成冲击效应,而且熊市的冲击程度要大于牛市。
4.从中介变量角度看,违约利差因子在冲击效应中起到的作用最大,上述实证结果发现无论牛市还是熊市中,对违约利差因子更敏感的公司,其股票收益率受到货币市场利率及利率预期波动的冲击程度更大。其次是投资者情绪,βsent的回归系数的显著性表明即期利率、短期利率预期波动在牛熊市环境下的冲击效应,在对情绪变化更加敏感的样本股票中影响更为明显。系统风险、期限利差因子作用相对较弱,只是在熊市环境下即期利率和短期利率波动的冲击效应中扮演显著的传递作用。这些结论表明,货币市场利率波动对股票收益的影响很大程度上是通过对投资者情绪和信贷环境预期的影响来实现的。
五、研究总结
货币市场的利率波动会影响股票市场收益率,这一结论已经得到广泛的理论和实证检验。但这种影响效应的机制和中介变量是什么一直没有得到很好的解答。本文通过构建货币市场利率及利率预期、投资者情绪等衡量指标,将货币市场利率变化对股票收益率的冲击效应进行分解,并在不同市场环境下对这些中介变量所起到的传导作用进行了总结分析。本文的主要结论有:
1.货币市场利率水平、利率预期波动都会对股市收益率以及投资者情绪、信贷环境预期等中介变量产生显著的冲击效应。具体来说,即期利率波动、长短期利率预期波动对股市收益率的影响效应比较显著;投资者情绪、信贷环境预期只对即期利率波动和短期利率预期波动表现出了显著性的反应,受长期利率波动的影响效应较弱;期限溢价只在熊市环境中受即期利率和短期利率预期的影响较为显著。
2.在不同的市场环境下,货币市场利率及预期波动的冲击效应显示出非对称性,熊市中股市收益和投资者情绪等中介变量更容易受到利率及利率预期波动的影响。这种对冲击的异质性反应间接表明,熊市中的投资者在市场流动性紧张的情况下,相信并且非常依赖货币当局救市的行为。
3.通过对397只样本股票的面板数据分析结果证明,那些收益率对投资者情绪、信贷环境预期、系统风险和期限利差因子更敏感的样本股票,其收益率更容易受到货币市场利率及利率预期的影响。
总之,本文研究结果表明货币市场利率波动对股票收益率的影响至少部分是通过对投资者情绪、信贷环境预期等中介变量的影响来实现的。在一个由投资者行为驱动的低效率股市中,投资者的预期和情绪在货币市场利率变动对收益率的影响机制中扮演着重要的传递角色。
